More than 3 years have passed since last update.

PCR検査の精度が悪いなら、繰り返し検査すれば良いじゃない？

Last updated at 2020-04-17Posted at 2020-04-17

はじめに

Qiita にもコロナウィルスのPCR検査の信頼性に関する投稿がいくつか見受けられます。

これらはどれも正しいと思うけど、実際は複数回検査するよね。
そしたらPCR検査がそれほど感度が高くなくても、特異度が完璧でなくても、意味があるんじゃないの？複数回検査することで、どれくらいよくなるの？・・・と言う疑問をもったので調べてみました。

改めて用語の定義

論文などでよく示されるのが、検査の感度 (sensitivity) と特異度 (specificity) です。

一方、COVID-19でPCR検査をした方が良いとか、よくないとかの議論で重要になるのが、
検査結果が陽性の時に実際にウィルスに罹患している確率である 陽性的中率 (positive precision)¹ と、
検査結果が院生の時に実際にはウィルスに罹患していない確率である 陰性的中率 (negative precision)。

これから示すように、これらの値は事前確率 (prior probability) に依存して大きく変わります。

検査の感度(sensitivity): 罹患している人を検査した時、検査結果が陽性となる確率。
検査の特異度(specificity): 罹患していない人を検査した時、検査結果が陰性となる確率。
事前確率(prior probability): 検査する前に、検査対象の人が罹患している確率。
陽性的中率(positive precision value): 検査で陽性となった人が、実際に罹患している確率。
陰性的中率(negative precision value): 検査で陰性となった人が、実際に罹患していない確率。

これを分割表 (contingency table) っぽく書くと以下のようになります²。

		真の状態
		罹患	非罹患
検査結果	陽性	$$ \begin{matrix} \text{真陽性} \\ \text{(true positive)} \\ \end{matrix} = a $$	$$ \begin{matrix} \text{偽陽性} \\ \text{(false positive)} \\ \end{matrix} = b $$	$$ \begin{matrix} \text{陽性的中率} \\ \text{(positive precision)} \\ \end{matrix} = \frac{a}{a+b} $$
検査結果	陰性	$$ \begin{matrix} \text{偽陰性} \\ \text{(false negative)} \\ \end{matrix} = c $$	$$ \begin{matrix} \text{真陰性} \\ \text{(true negative)} \\ \end{matrix} = d $$	$$ \begin{matrix} \text{陰性的中率} \\ \text{(negative precision)} \\ \end{matrix} = \frac{d}{c+d} $$
		$$ \begin{matrix} \text{感度} \\ \text{(sensitivity)} \\ \end{matrix} = \frac{a}{a+c} $$	$$ \begin{matrix} \text{特異度} \\ \text{(specificity)} \\ \end{matrix} = \frac{d}{b+d} $$

陽性的中率、陰性的中率

感度 (sensitivity) = $\frac{a}{a+c}$ と　特異度 (specificity) = $\frac{d}{b+d}$ と　事前確率 (prior probability) = $\frac{a+c}{a+b+c+d}$ が与えられていると仮定します。
サンプルの総数 $a+b+c+d=1$ とでも置いて、陽性的中率、陰性的中率を求めると、

$$
\text{positive precision} = \frac{
\text{sensitivity} \cdot \text{prior probability}
}{
\text{sensitivity} \cdot \text{prior probability} + (1 - \text{specificity}) * (1 - \text{prior probability})
}
$$

$$
\text{negative precision} = \frac{
\text{specificity} \cdot (1 - \text{prior probability})
}{
(1 - \text{sensitivity}) \cdot \text{prior probability} + \text{specificity} \cdot (1 - \text{prior probability})
}
$$

となります³。

以後は、この記事に習って、PCR検査の感度 (sensitivity) = $0.70$, 特異度 (specificity) = $0.95$ と仮定して計算しましょう。

import matplotlib.pyplot as plt
import numpy as np

sensitivity = 0.70  # 1回の検査の感度。罹患している時に検査が陽性になる確率。
specificity = 0.95  # 1回の検査の特異度。罹患していない時に検査が陰性になる確率。

def positive_precision(prior_probability, sensitivity, specificity):
    '''
    Args:
        prior_probability: 事前確率。前提条件がないときに罹患している確率。
        sensitivity: 感度。罹患している患者を検査したときに、陽性となる確率。
        specificity: 特異度。罹患していない患者を検査したときに、陰性となる確率。
    Returns:
        positive_precision: 陽性的中率。検査結果が陽性だった時に、実際に罹患している確率。
    '''
    return sensitivity * prior_probability / (sensitivity * prior_probability + (1 - specificity) * (1 - prior_probability))

def negative_precision(prior_probability, sensitivity, specificity):
    '''
    Args:
        prior_probability: 事前確率。前提条件がないときに罹患している確率。
        sensitivity: 感度。罹患している患者を検査したときに、陽性となる確率。
        specificity: 特異度。罹患していない患者を検査したときに、陰性となる確率。
    Returns:
        negative_precision: 陰性的中率。検査結果が陰性だった時に、実際に罹患していない確率。
    '''
    return specificity * (1 - prior_probability) / ((1 - sensitivity) * prior_probability + specificity * (1 - prior_probability))

ここで関数 positive_precision() と negative_precision() はその名の通り、それぞれ陽性的中率と陰性的中率を、引数で与えられる事前確率、感度、特異度から求めます。

n回検査を行なってn回全て陰性だったら、陰性と考える場合

つまり、何回か検査して1度でも陽性が出たら陽性とする、悲観的な考え方に基づく場合を考えましょう。
事前確率 (prior probability) と検査回数 $n$ を変化させてグラフにプロットしてみます。

def sensitivity_pessimistic(sensitivity, n):
    '''
    Args:
        sensitivity: 1回の検査の感度
        n: 検査回数
    Returns:
        n回検査の感度: n回検査して全て陰性だったら、陰性と考える検査の感度
    '''
    return 1 - (1 - sensitivity) ** n

def specificity_pessimistic(specificity, n):
    '''
    Args:
        specificity: 1回の検査の特異度
        n: 検査回数
    Returns:
        n回検査の特異度: n回検査して全て陰性だったら、陰性と考える検査の特異度
    '''
    return specificity ** n

xs = [ np.exp(-0.05 * i) for i in range(0, 200)]
ys_list = []
legend_list = []
for n in [1, 3, 5]:
    ys_list.append([ positive_precision(x, sensitivity_pessimistic(sensitivity, n), specificity_pessimistic(specificity, n)) for x in xs ])
    legend_list.append('検査{}回実施時の陽性的中率'.format(n))
for n in [1, 3, 5]:
    ys_list.append([ negative_precision(x, sensitivity_pessimistic(sensitivity, n), specificity_pessimistic(specificity, n)) for x in xs ])
    legend_list.append('検査{}回実施時の陰性的中率'.format(n))

fig, ax = plt.subplots()
plt.xscale('log')

for ys in ys_list:
    ax.plot(xs, ys)
ax.legend(legend_list)
ax.set_xlabel('罹患事前確率')
ax.set_title('複数回PCR検査の的中率 (n回検査して全て陰性なら陰性)')
plt.show()

この悲観的な「１回でも陽性が出たら罹患している」と言う考え方は、現在の社会の受け止め方に近いのではないかな。
これは安全サイドに振っているので良さそうに思うかもしれませんが、事前確率が低い時には、実際には罹患していない大量の人を罹患者として扱ってしまうことになり得ます。病院や隔離施設がパンクして大変なことになるかもしれません。

例えば、今日 (2020/4/18) 現在の日本の確定感染者数⁴ は 9,000名余りですが、仮にこの10倍の 100,000人 ($10^5)$ の真の感染者が存在しているとします。日本の総人口を 1億人 ($10^8$) だとすると、ランダムに選んだ人の事前確率は、
$$
\text{事前確率 (prior probability)} = \frac{真の感染者数}{総人口} = \frac{10^5}{10^8} = 10^{-３}
$$
であり、上のグラフで横軸が $10^{-3}$ のところを読むと分かるように、デタラメに選んだ人を検査したところで、なんの意味もないと言っても過言ではない、と言ったら言い過ぎでしょうか。

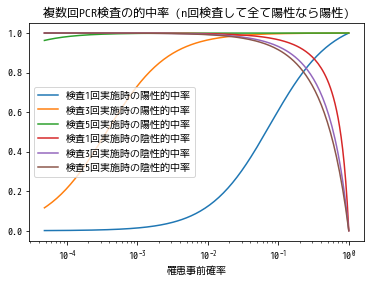
n回検査を行なってn回全てが陽性だったら、陽性だと考える検査の場合

次に真逆に振って、1度でも陰性が出たら陰性と考える、とても楽観的な考え方を取ったらどうなるでしょう。
事前確率 (prior probability) と検査回数 $n$　を変化させてグラフにプロットしてみます。

def sensitivity_optimistic(sensitivity, n):
    '''
    Args:
        sensitivity: 1回の検査の感度
        n: 検査回数
    Returns:
        n回検査の感度: n回検査してn回全て陽性だった時、陽性であると考える検査の感度
    '''
    return sensitivity ** n

def specificity_optimistic(specificity, n):
    '''
    Args:
        specificity: 1回の検査の特異度
        n: 検査回数
    Returns:
        n回検査の特異度: n回検査してn回全て陽性だった時、陽性であると考える検査の特異度
    '''
    return 1 - (1 - specificity) ** n

xs = [ np.exp(-0.05 * i) for i in range(0, 200)]
ys_list = []
legend_list = []
for n in [1, 3, 5]:
    ys_list.append([ positive_precision(x, sensitivity_optimistic(sensitivity, n), specificity_optimistic(specificity, n)) for x in xs ])
    legend_list.append('検査{}回実施時の陽性的中率'.format(n))
for n in [1, 3, 5]:
    ys_list.append([ negative_precision(x, sensitivity_optimistic(sensitivity, n), specificity_optimistic(specificity, n)) for x in xs ])
    legend_list.append('検査{}回実施時の陰性的中率'.format(n))

fig, ax = plt.subplots()
plt.xscale('log')

for ys in ys_list:
    ax.plot(xs, ys)
ax.legend(legend_list)
ax.set_xlabel('罹患事前確率')
ax.set_title('複数回PCR検査の的中率 (n回検査して全て陽性なら陽性)')
plt.show()

このように、複数回検査することで、例え事前確率がとても低い場合でも、陽性である確からしさを大きく高めることができました。

言うまでもない事ですが、高熱が出ているとか、肺炎になっていると言った症状があれば、COVID-19に罹患している事前確率が高まっているので、検査することに大いに意味があります。上の２つのグラフどちらをとるにしても、陽性的率、陰性的合率が高くなるからです。

まとめ

PCR検査が１回でも陽性となった人は、感染者として扱われてしまいそうですが、普通の人はまだそこまで事前確率が高くないので、即有罪確定にはならないと言うことだと思います。実際の臨床現場ではおそらく、他の症状（肺炎、味覚嗅覚異常など）を見て検査する人(=事前確率が十分高い人）を選んで検査しているのでしょう。

また、病院から退院するときはちゃんと、複数回PCR検査を行って、２回連続陰性だったら退院と言った運用がなされているような感じなんでしょうか。

知らんけど。

github 上に jupyter notebook を置きました。間違ってたらごめんね。

「陽性的・中率」ではなくて、「陽性・的中率」です。 ↩
表の修飾がうまくできません。Markdownで変わったことするのは素人には難しいなぁ。 ↩
どうしてかって？この記事のようにベイズの定理を使っても良いし、４個変数があって４本式があるから、連立方程式を解けば良いよ。 ↩
定義はよくわかりませんが、自治体が発表した数で、おそらくPCR検査で １回でも 陽性と出た人の数じゃないかと思われます。 ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up