ほとんどのDB正規化の記事は、実用性がないか間違っている。

新しくリレーショナルデータベースを勉強した人が、データベースの正規化 (normalization) に関する記事を書いてくれています。その多くのケースで、教科書に書いてある定義に従って、第一正規形は・・・、第二正規形は・・・、第三正規形は・・・とそれぞれが満たすべき条件だけを述べています。

正規形の条件はその通り。教科書に間違ったことは書いてありません。あなたの記憶は正しい。しかし、正規形でないデータが手元にあった時、どうやったら正規形に変換できるのでしょう？正規形の条件を正しく知っていたからと言って、正規形に変換できるとは限らないのです。これは寿司の条件（小ぶりの酢飯の塊の上に、魚の切り身が乗っている）を知っていたからと言って、寿司が握れるとは限らないのと同じことで、当たり前です。

正規形・正規化をマスターしたと自称するためには、どんな捻くれたデータが与えられたとしても、毎回必ず、間違いなく、（できれば試行錯誤せずに）、第3正規形かボイスコッド正規形に変換できなければならないはずです。

この記事では、与えられた非正規形データを必ず第三正規形、ボイスコッド正規形に変換する(=正規化する)、実践的な方法を理解することを目指したいと思います。

以下では、「第n正規形」って書くと長いので、1NF(第一正規形), 2NF(第二正規形), 3NF(第３正規形), BCNF(ボイスコッド正規形)と略記します。NFはnormal formの略です。

正規形の定義を憶えていても、正しく正規化できない

そもそも、正規化前の元のデータを、正規形に変換するとはどういうことなのでしょうか？少し長くなりますが、説明してみます。

2NFの条件は多くの教科書で「1NFであって、部分従属性が存在しない。すなわち、すべての非キー属性が主キー属性に完全に関数従属する。」と書いてあると思います。

自分で例を考えるのが面倒なので、OSS-DB道場さんの例を借用引用しましょう。

このテーブルには以下の矢印で表される関数従属性があると仮定されています。

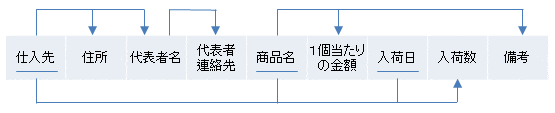
これは部分従属性が存在するので2NFではありません。具体的には例えば、主キー {仕入先, 商品名, 入荷日} の一部である仕入れ先によって、代表者氏名や代表者連絡先が決まるというのが部分従属性です。

では、どうやれば部分従属性がなくなるでしょう？

テーブルを横に分割すればいいんでしたっけ？まあ、そうなのですが、2NFの条件を満たす分割方法はとてもたくさんあります。どれでも良いのでしょうか？

極端な例として、このテーブルを何も考えず隣り合う２カラムずつに分割するとどうなるでしょう。

{仕入先, 住所}テーブル、{住所, 代表者名}テーブル, {代表者名, 代表者連絡先}テーブル、{代表者連絡先, 商品名}テーブル、{商品名, 1個当たりの金額}テーブル、{１個当たりの金額, 入荷日}テーブル、{入荷日, 入荷数}テーブル、{入荷数, 備考}テーブルの８個のテーブルに分解されました。ちゃんと結合できるように、カラムを重複させています。一部だけ具体的な値を書いてみます。

仕入先	住所
津軽ファーム	青森県弘前市
みかん園	愛媛県松山市

住所	代表者名
青森県弘前市	陸奥太朗
愛媛県松山市	松山花子

１個あたりの金額	入荷日
150	2012-07-01
300	2012-07-01
150	2017-07-03
80	2012-07-02

さて、問題です。これらのテーブルは第何正規形になっているでしょう？

えっと・・・・一つのテーブルに２個しかカラムがないので、部分従属は存在しえないから、少なくとも2NFにはなってますね。実はそれどころか、必ずBCNFになっているのです。BCNFであるということは、3NFでもありますから、これで一気に正規化が完了したことになります¹。

本当でしょうか？ だめそうですよね。なぜですか？

ここで言いたかったのは、なんとなく適当に分解して、2NF, 3NF の条件を満たしていれば良いというものではない、ということです。今回は1NFを（でたらめに）2NFの条件を満たすように変換してみましたが、2NFから3NF/BCNFでも同様に、変換した結果がxNFの定義の条件を満たしていればよいというものではありません。

では、どこが悪かったのでしょう？

正規化する(＝正規形に変換する)時には、その「変換」が満たすべき条件があります。それは、

1. 自然結合すると元のテーブルに戻ること。
2. (できれば)存在する関数従属性が、どこかのテーブルで表現されていること

です。１を無損失分解と呼びます。元のデータの一部が消えてしまったり、別のものになったらデータベースとして意味ないですよね。だからこれは必ず満たさなければなりません。

２はデータベースは従属性を保存するために存在するとも考えられる²ので、従属性がわかりにくくなってしまうのは望ましくないからです³。それでも分解するとよいことがある場合があるので、ここでは「できれば」と表現しました。この記事では深入りしません。

上記のでたらめな2カラムテーブルへの分解は、1を満たすとは限らないから絶対だめというわけです。(ついでに2も満たしませんが。)

さて、どうすれば良かったのでしょうか?

正規化のアルゴリズム

ここでは、BCNFへの正規化のアルゴリズムを示すことが目標にします。アルゴリズムというのは、どんな入力が与えられてもその手順に従えば機械的に必ず目的の結果が得られる手順という意味です。BCNFへの正規化のアルゴリズムがあるということは、任意の1NFをBCNFに機械的に変換できるということです。一般にアルゴリズムはあらゆるケースを想定するので、人間にとってわかりやすいとは限りませんが、このアルゴリズムは人間にとっても覚えやすいものだと（私は）思います。

なぜ3NFではなくBCNFなのでしょう。実は３NFはBCNFに例外を認めた、ちょっと汚いNFなのです。BCNFに正規化できれば3NFに戻すことも簡単です。

準備

アルゴリズムを示す前に、用語や表記の定義をしておきましょう。

Rという名前のテーブルに、A, B, C というカラムが存在するとき、これを R(A, B, C) と書きます。

テーブルのカラムの間には関数従属性が存在することがあります。これも長いのでFD (functional dependency)と略します。例えば、学籍番号が決まると、学生の名前、住所など、学生に関する属性が一意に決ります。これを「学籍番号→学生名, 学籍番号→学生住所 というFDがある」と言います。この2つをまとめて、学籍番号→{学生名、学生住所} と表記することもあります。ある学生がある時間に取ることのできる授業は一つだけなので、{学籍番号, 日時}→授業番号 が成り立ちそうです。この時は、学籍番号だけでは授業は決まらず、日時だけでも授業は決まりません。両方が揃った時に授業が一意に決まります。

一般には「→」の両辺はどちらもカラムの集合ということになります。「テーブル R(A, B, C, ...) において、FD {A, B...}→{C, D...} が成り立つ」なんて言います。面倒なので集合を表す中かっこ{と}は省略することもあります。

テーブル R(A, B, ...) のスーパーキーとは、Rのカラムの部分集合で、Rの全カラムが関数従属するもののことです。

キー(または主キーまたは候補キーでも同じ)は、スーパーキーの部分集合であって、そのどの要素を取り除いても、スーパーキーでなくなるもののことです。言い換えると、キーは極小のスーパーキーです。

このように、キーは存在する関数従属性によって定義されます。逆ではありません。

次の概念が一番ややこしいのですが⁴、カラム集合$X$の閉包(closure)という概念を導入します。あるテーブルRのカラム集合$X$に対して、$X$の閉包$X^{+}$とは、$X$自身から出発して、$X$に関数従属するカラム$A$があったらそれをどんどん加え($X^{+} = X^{+} \cup {A}$)ていき、それ以上大きくできなくなったカラム集合を指します。
例えば、$A\rightarrow BC$, $C\rightarrow D$ だった時、$A^{+}$ は、はじめ$A$自身から出発して、$A\rightarrow BC$だから{$A, B, C$}と大きくなり、次に $C\rightarrow D$を考慮して、{$A, B, C, D$} になります。これ以上FDがないので、$A^+={A, B, C, D}$となります。

確認ですが、キーもスーパーキーも、定義からわかるように、カラムの集合です。あるカラムの集合$X$の閉包$X^+$がテーブルRの全カラムになる時、その$X$はRのスーパーキーとなります。

アルゴリズム

ではアルゴリズムを示します。

Step-1: スーパーキーを見つける

まず、与えられたテーブルのスーパーキーを全て求めます。他のカラムに関数従属していないカラムはスーパーキーの一部になります。
上の例では、仕入先、商品名、入荷日は他のどのカラムにも関数従属していないので、必ずスーパーキーの一部になります。$X$={仕入先、商品名、入荷日}として、$X$がスーパーキーになっているかどうか調べるには、その閉包$X^+$を求めます。

• {仕入先}→{住所, 代表者名}なので、住所と代表者名も閉包に追加します。現在のところ$X^+$={仕入先、商品名、入荷日、住所、代表者名}。
• 代表者連絡先は、閉包の一部である代表者名に関数従属しているので、これも閉包に追加します。現在のところ$X^+$={仕入先、商品名、入荷日、住所、代表者名、代表者連絡先}。
• 商品名→一個当たりの金額, 備考より、これらを追加して、現在のところ$X^+$={仕入先、商品名、入荷日、住所、代表者名、代表者連絡先、一個当たりの金額、備考}。
• さらに、{仕入先、商品名、入荷日}→{出荷数} より出荷数も追加すると、$X^+$={仕入先、商品名、入荷日、住所、代表者名、代表者連絡先、一個当たりの金額、備考、出荷数}と、このテーブルの全カラムになりました。

閉包が全カラムになるものがスーパーキーでしたから、{仕入先、商品名、入荷日}はスーパーキーだということが確認できました。元々そう書いてあったんだから当たり前だって？そうですね。このケースではこんな手間をかけなくてもわかりますが、意味がよくわからないテーブルでも曖昧性なく実行できなければならないのがアルゴリズムなので、我慢してください。

蛇足ですが、スーパーキーの定義から、{仕入先、商品名、入荷日}に任意のカラムを追加したものも、スーパーキーです。一番小さいスーパーキーがキーでしたね。この場合、{仕入先、商品名、入荷日}から一つでも要素を取り除くとスーパーキーにならないので、これはキーでもあります。

テーブルに存在する関数従属性の組み合わせによっては、複数キーが存在することがありますので、注意してください。その場合はBCNFが3NFと一致しません。逆に、１種類しかキーが存在しないなら、BCNF=3NFです。

Step-2: BCNFの定義に違反するFDを見つける

さて、BCNFの定義を思い出しておきましょう。

R に存在する全ての関数従属性 $X\rightarrow A$ について、

1. $A \in X$ であるか、または
2. $X$ がRのスーパーキーであるとき、

その時に限り、R は BCNF である。

皆さんの知っているものと異なる？そうかもしれませんが、その定義と同値です。これが便利な定義なので、これを受け入れてください。

さて、与えられたFDの中から、上の定義に違反するFDを一つ見つけます。

今回の例ではたくさんあってどれでもいいのですが、ここでは 商品名→一個当たりの金額 を選びましょう。この右辺は左辺の一部ではありません(BCNFの定義1違反)し、左辺はスーパーキーではありません (BCNFの定義2違反）ので、BCNF違反です。

もしBCNF違反のFDがなければ、RはBCNFなのでアルゴリズムは終了します。

Step-3: テーブルを分解する

そうしたら、違反しているFD $X\rightarrow A$ の左辺 $X$ の閉包 $X^+$ を求めます。{商品名, １個当たりの値段, 備考} となりますね。

そしたら、元のテーブルRの全カラムを$R$と表すことにして、元のテーブルを $R_1=X^+$ と $R_2=(R-X^+)\cup X$ に分解します。この例では、$R_1$={商品名, １個当たりの値段, 備考}、$R_2$=全カラムから$X^+$を除いて$X$を加えたもの={仕入先、住所、代表者名、代表者連絡先、商品名、入荷日、入荷数} に分解されました。

商品名	１個当たりの値段	備考
...	...	...

仕入先	住所	代表者名	代表者連絡先	商品名	入荷日	入荷数
...	...	...	...	...	...	...

これらはBCNFなのでしょうか? 確かめてみましょう。

$R_1$に存在するFDは、商品名→一個当たりの金額 と 商品名→備考 だけです。両方とも左辺がこのテーブルのスーパーキーなので、BCNFの定義を満たします。よってBCNFでした。

$R_2$はどうでしょう？ 残念ながら、まだBCNF違反のFDがあります。仕入先→住所 は左辺がスーパーキーではないのでBCNF違反です。だめじゃん。いいえ、そういう時は、この Step-２ を繰り返し適用します。やってみましょう。

左辺(=仕入先)の閉包を求めます。{仕入先, 住所, 代表者, 代表者連絡先} となりました。よって $R_{21}$={仕入先, 住所, 代表者, 代表者連絡先} と$R_{22}$={仕入先, 商品名, 入荷日, 入荷数} に分解することになります。

仕入先	住所	代表者名	代表者連絡先
...	...	....	....

仕入先	商品名	入荷日	入荷数
...	...	...	...

実はまだ終わっていない⁵。$R_{21}$にはBCNF違反のFDが残っています。そう、代表者名→代表者連絡先です。この左辺の閉包を求めて $R_{211}$={代表者, 代表者連絡先}, $R_{212}$={仕入先, 住所, 代表者} と分解されます。

代表者名	代表者連絡先
....	....

仕入先	住所	代表者名
...	...	....

これ以上BCNFに違反するFDがないので、これで終了です。

はぁー。疲れた。

補足とまとめ

予想通り、自分史上最長の記事になってしまいました。

アルゴリズムを短くまとめて書いてみると、

1. $R$のスーパーキーを見つける。
2. $R$にBCNF違反のFD $X\rightarrow A$を探す。存在しなければ終了。
3. $R$を$R_1=X^+$と$R_2=(R-X^+)+X$に分解する。

$R_1$と$R_2$は$X$が「のりしろ」になって、結合すると元の$R$に無損失で戻ります。
$R_1$, $R_2$がBCNF出なかった時は、この手順を繰り返します。

なになに、俺は3NFにしたいんであって、BCNFにしたいんじゃない？ そうでしたね。でも、上にも書いたけど、3NF$\not=$BCNFになるのは、キーが複数存在する時だけです。で、そんな場合は、3NFの定義を思い出して、このアルゴリズムのBCNFを3NFと読み替えて同じことをすれば良いです。ただし3NFの定義は以下の通り。

R に存在する全ての関数従属性 $X\rightarrow A$ について、

1. $A \in X$ であるか、または
2. $X$ がRのスーパーキーであるか、または
3. $A$ がキーの一部である時、

その時に限り、R は 3NF である。

また俺の知ってる定義と違うって？それと同値なので、こちらを(も)憶えておいてもらえると、アルゴリズムと整合性が取れて、全体的に憶えやすいと思います。

追加の想定問答:

• このアルゴリズム停止するの？ はい。必ずテーブルは小さくなっていくので、最後は2カラムテーブル(=BCNF)になります。
• 証明がない?ごめんね。誌面の都合です。私を信じなさい。
• 2NFが出てこなかったけどいいの？ はい。このアルゴリズムを憶えておくと、2NFの存在意義はありません。1NFから出発して必ずBCNF(or 3NF)が得られます。
• じゃあ、1NF変換するにはどうすれば？ 1NFに関しては定義をそのまま適用すれば1NFになる気がするので、どうぞ勝手にやってください。

長いから読んでもらえんな、こりゃ。知らんけど。

1. ちなみに、どんな２カラムテーブルも必ずBCNFです。大学のテストなら証明せよという問題が出るかもしれません。 ↩

2. 例えば学籍番号が決まると生徒の名前が決まるという関数従属性があったおき、神様でない私たちはこの「関数」を計算することができません。だから、データベースに保存しておくわけです。 ↩

3. BCNF以上に分解すると関数従属性が保存できないことがあります。 ↩

4. その代わりと言ってはなんですが、遷移的関数従属性とか完全従属とか言う概念は使いません。いっそ2NFも必要ありません。 ↩

5. この例では代表者が複数の仕入先を代表する可能性があるという(ある意味不自然な)仮定がされているためです。代表者が複数の企業を兼任しているなら、それぞれ別の電話番号を持っている気がします。だからこっから先は蛇足かもしれませんが、OSS-DB道場の仮定に従って続けます。 ↩