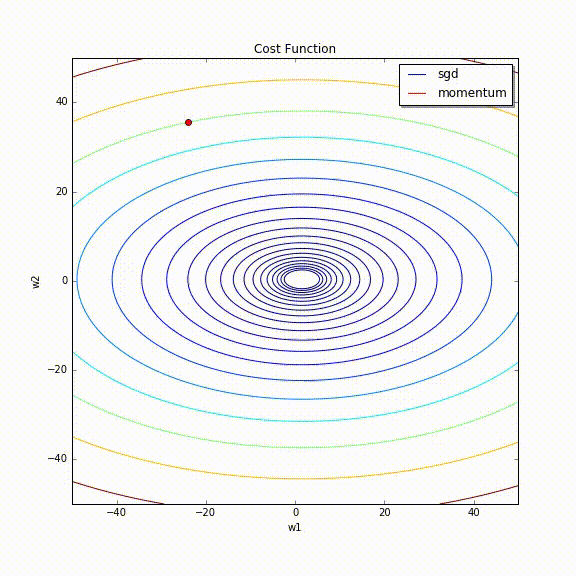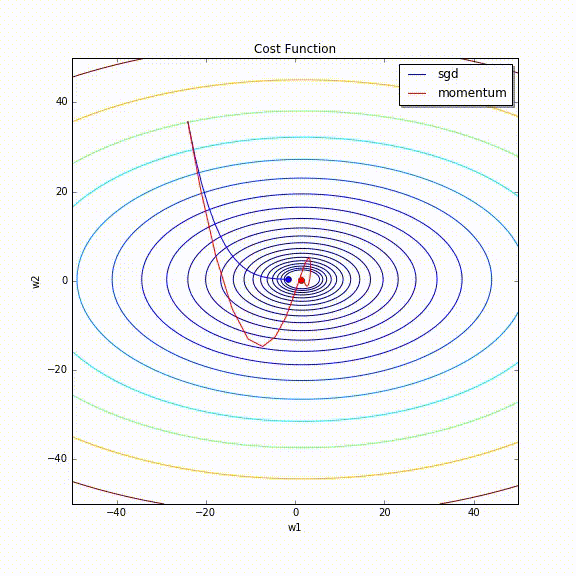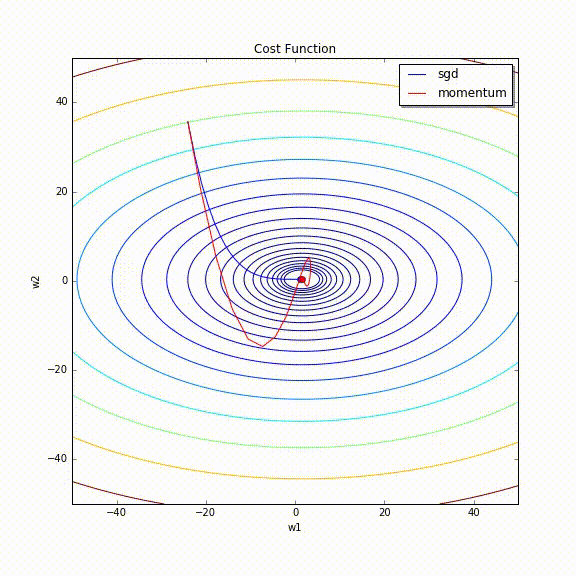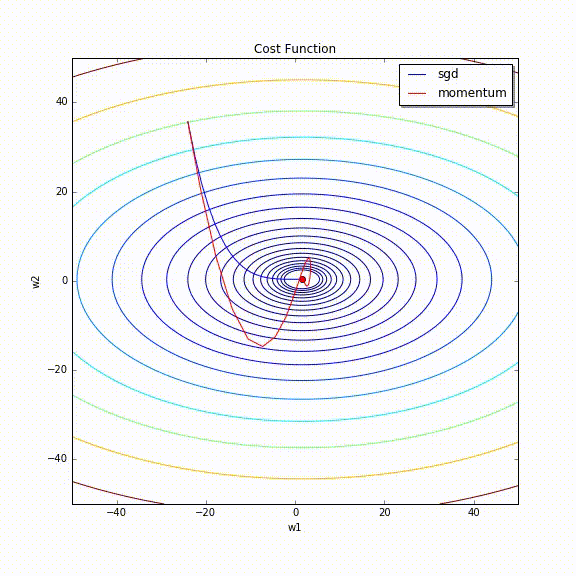
Momentumは、Parameterの更新を改善する手法です。
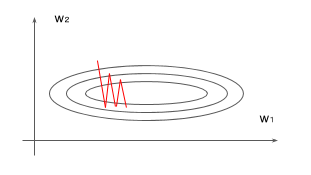
よくMomentumで出てくる話が、loss functionの空間が下記のように横長の場合に、
垂直方向から更新されてくると更新が行ったり来たり（Oscillation）することがあります。
Momentumにはこれを抑制する効果があります。
loss functionの空間は、Neural NetworkではWeightやbiasのようなParameterによって描かれる空間です。
いわゆる下記のような勾配降下法のweightの更新式の$C(w)$のことです。
w \leftarrow w -\eta \frac{\partial C(w)}{\partial w}
Momentumでは、更新がOscillationしないように前回の更新量のいくらかを加算します。
上の図で言うと、例えば「前回下の方向に移動していたら、次も下の方向の可能性が高いんじゃない」という感じで補正項を加えます。
式で書くと下記のようになります。
\begin{equation}
w_{t+1} = w_{t} - \eta \frac{\partial C(w)}{\partial w} + \mu\Delta w_{t-1}\\
\end{equation}
これでも十分にわかりやすいですが、もう少しわかり易くするために、新しい変数$v$を導入して、
上の式を$w$と更新量$v$に分けてみます。
そうすると上記の式は下記のようになります。
\begin{equation}
w_{t+1} = w_{t} + v_{t}\\
v_{t} = \mu v_{t-1} - \eta \frac{\partial C(w)}{\partial w}
\end{equation}
Parameter $w$の更新はまず
- $v$を前回の$v$とgradientにより更新
- 得られた新しい$v$をParameter $w$に足す
という感じになります。
実際にMomentumありとなしでの挙動をAnimationにしてみました。
たしかにMomentumなしは更新がOscillationしていますが、MomentumありだとしばらくするとOscillationが収まっています。
更新量を加えている分少し行き過ぎることもあります。
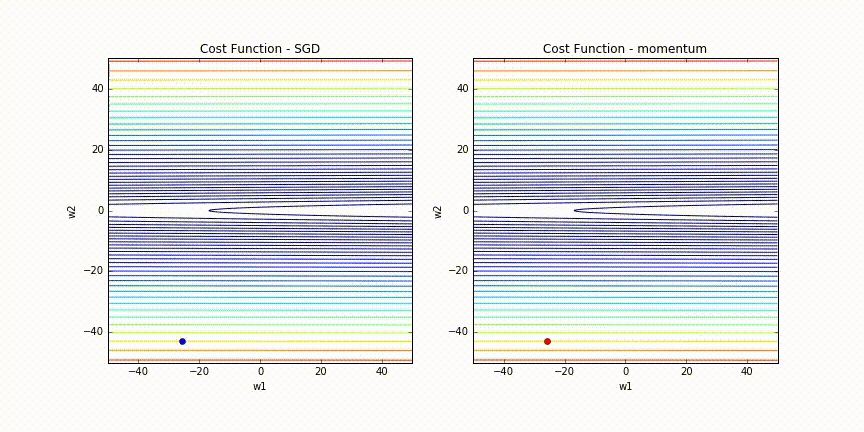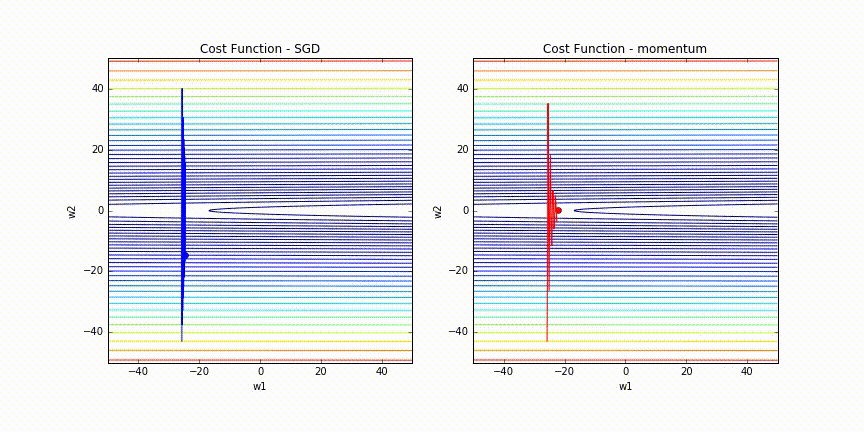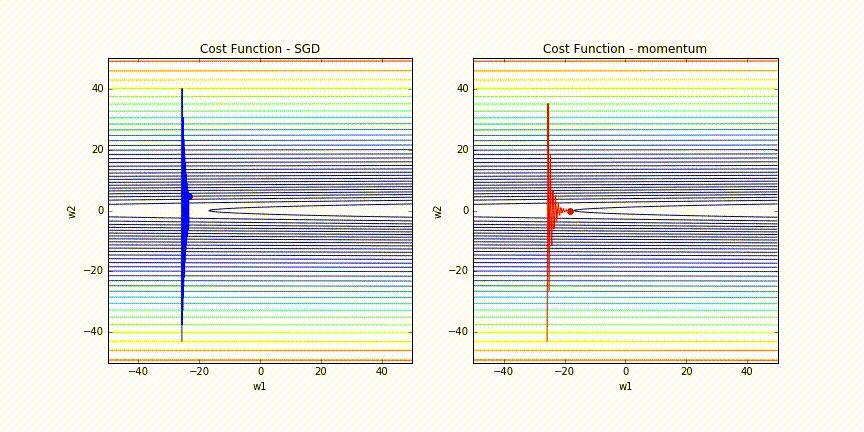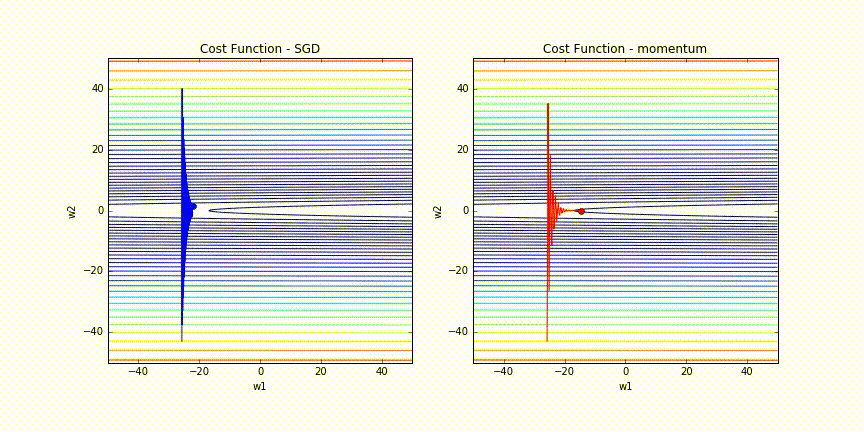
このAnimation gifは、Alec RadfordさんのOptimizationの比較アニメーションにinspireされて作ってみました。