[Python]多項式によるカーブフィッティング

サンプルデータに対し多項式でカーブフィッティングしたいときはnumpyのpolyfitを使うと簡単にできる。曲線は下記の多項式で表される。polyfitは下の式の$a_n$を計算してくれる。

y = \sum^{N}_{n=0} a_n x^n

polyfitで返される値は次数が高い方ほうから並んでいる。数式にすると下記のような感じになる。

y = \sum^N_{n=0} a_n x^{N-n}

polyfitで取得した係数を使った曲線のグラフを書きたいときは,xの値をnumpy.linspace等で用意して、numpy.polyvalに係数とxを渡すとyを計算してくれる。

下図はサンプルデータと１次式でカーブフィッティングした結果
numpy.polyfit(x,y,1)とするだけで係数が得られる。x,yはデータで1は次数を表す。

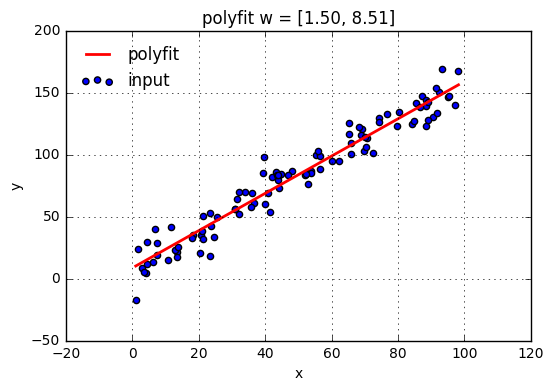
w = np.polyfit(x,y,1)
xs = np.linspace(np.min(x),np.max(x),100)
ys = np.polyval(w,xs)

fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(x, y,label='input')
ax.plot(xs, ys, 'r-', lw=2, label='polyfit')
ax.set_title('polyfit w = [%.2f, %.2f]' % (w[0],w[1]))
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend(loc='best',frameon=False)
ax.grid(True)

サンプルデータは下記のように作成した。

def getData1(numPoints, w,b, nstdev, xmin=0.0, xmax=1.0 ):
    x = scipy.stats.uniform.rvs(loc=xmin, scale=xmax-xmin,size=numPoints)
    n = scipy.stats.norm.rvs(size=numPoints, scale=nstdev)

    y = w * x + b + n
    return x, y

x, y = getData1(100, 1.5, 10, 10, xmin=0, xmax=100)

3次多項式でカーブフィッティングした結果

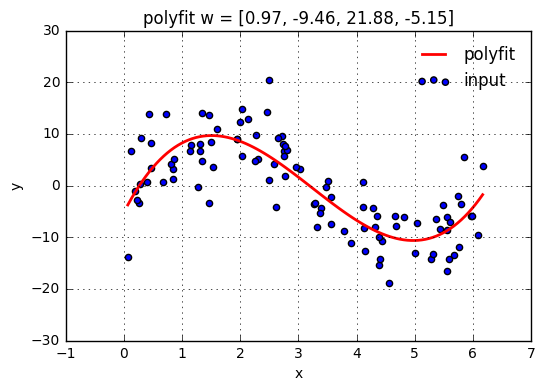
w = np.polyfit(x,y,3)

xs = np.linspace(np.min(x),np.max(x),100)
ys = np.polyval(w,xs)

fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(x, y,label='input')
ax.plot(xs, ys, 'r-', lw=2, label='polyfit')
ax.set_title('polyfit w = [%.2f, %.2f, %.2f, %.2f]' % (w[0],w[1],w[2],w[3]))
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend(loc='best',frameon=False)
ax.grid(True)

サンプルデータは下記のように作成した。

def getData2(numPoints, Amp,  freq, phase, nstdev, xmin=0.0, xmax=np.pi*2.0 ):
    x = scipy.stats.uniform.rvs(loc=xmin, scale=xmax-xmin,size=numPoints)
    n = scipy.stats.norm.rvs(size=numPoints, scale=nstdev)

    y = Amp*np.sin(freq * x + phase) + n
    return x, y

x, y = getData2(100, 10, 1.0, 0.0, 5, xmin=0, xmax=np.pi*2.0)

参考URL
https://docs.scipy.org/doc/numpy/reference/generated/numpy.polyfit.html
https://docs.scipy.org/doc/numpy/reference/generated/numpy.polyval.html#numpy.polyval