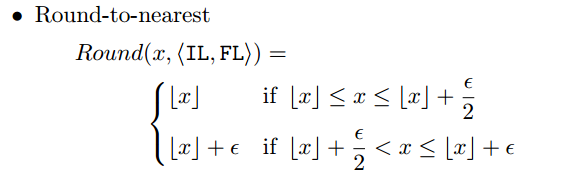Deep Learning with Limited Numerical Precision
Deep Learningを固定小数点(Fixed Point)演算で行った時の精度と性能の検証及びFPGAでの実装に関する論文。
論文では16bit Fixed Point演算で32bit Floating Pointと同等の性能を達成している。
Fixed pointのメリットは、
・Floating Pointに比べて高速に演算ができ、H/W Costが少ない
・メモリの消費を抑えられる(16bit Fixed Pointと32bit Floating Pointとの比較での話)
固定小数点の表記
論文で使用している表記は以下の通り
Fixed Point = [QI.QF]
QI ... integer
QF ... fractional part
IL ... # of integer bits
FL ... # of fractional bits
WL ... word length WL = IL + FL
Fixed Pointの表記は**<IL, FL>**を使用
固定小数点の値の幅は
$[-2^{IL-1}, 2^{IL-1}-2^{-FL}]$
例えばIL=8, FL=8の時
$[-2^7, 2^7-2^{-8}]$
範囲の最大値の意味は$2^7$から小数の最小値$2^{-8}$を引いたということ。
Rounding Mode
固定小数点計算の場合に四捨五入(Round)の扱いが問題になる。
四捨五入は2つのModeで検証した
Round-to-nearest
普通の四捨五入
ここで$\epsilon=2^{-FL}$のこと
$\lfloor x \rfloor$は$x$を超えない最も近い整数値
$\lfloor x \rfloor$は$x$以下の$\epsilon=2^{-FL}$を整数倍した値
$FL=1$のとき$\epsilon=0.5$なので
$x=1.75$だったら$\lfloor x \rfloor=1.5$
$x=1.8$だったら$\lfloor x \rfloor=2.0$
になる。
Stochastic rounding
ramdomでどっちにするか決める。その時の確率は$x$と$\lfloor x \rfloor$の差を$\epsilon$で割ったもの。
Convert ( clipping)
値が範囲外だった時の処理
最小値以下だったら最小値に、最大値以上だったら最大値にする。
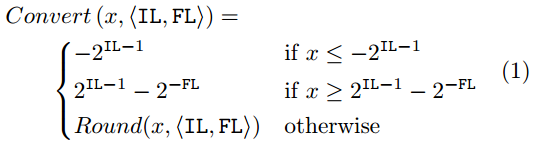
Multiply and accumulate(MACC) operation
要素毎に掛け算して、総和を取る演算
z=\sum_{i=1}^d a_ib_i
2つの値の掛け算後の値は<2IL,2FL>になる。毎回四捨五入すると精度が落ちるので、専用のTemporal Registerを使って演算する。
必要なビット精度は、$log_2d+2WL$
性能評価
MNIST
Networkの構造、学習パラメータは以下の通り
・2 hidden layer
・1000 unit ReLU
・training image 60,000, test image 10,000 28x28
・imput data range [0,1]
・data augmentatoinなし
・weight N(0,0.01)、bias 0 で初期化
・minibatch size 100
・SGD
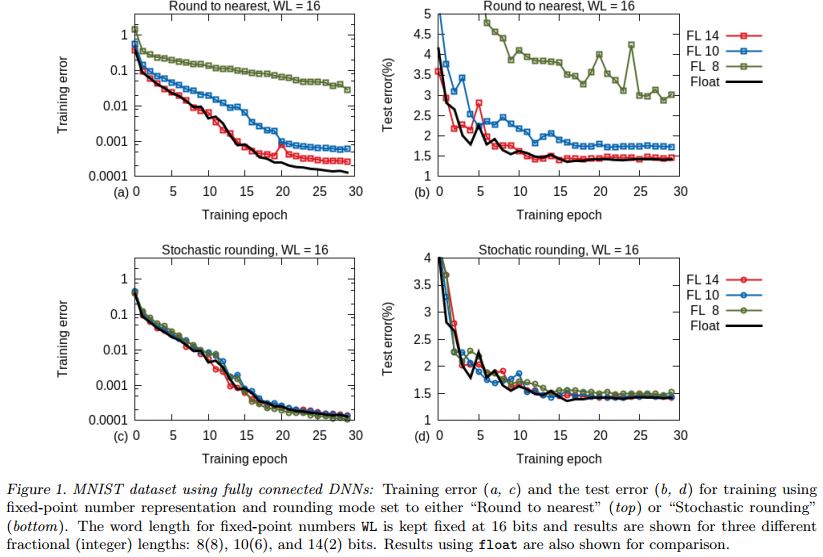
Round to nearestだとFL=8,10,12で劣化が見られる。
パラメータがほとんど0になっているのが原因とのこと。
Stochastic roundingだとFL=8でも大きな劣化が見られない。
CNN
・MNIST
・2 convolutional layer
・5x5 filter
・ReLU
・first layer 8 feature maps, second layer 16 feature maps
・max pooling 2x2 non-overlapping
・fully connected layer 128 ReLU
・10-way softmax
・exponentially decreasing learning rate 0.95/epoch
・first learning rate 0.1
・Momentum 0.9
・weight decay 0.0005
・SGD
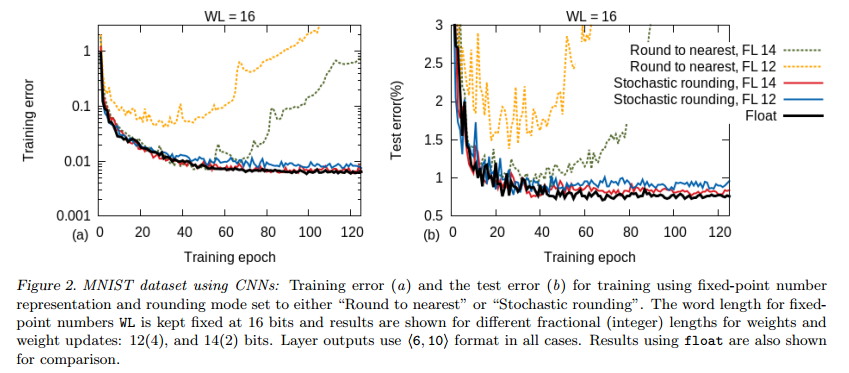
Stochastic roundingだとFL=12,14でFloatingと同じぐらいの性能
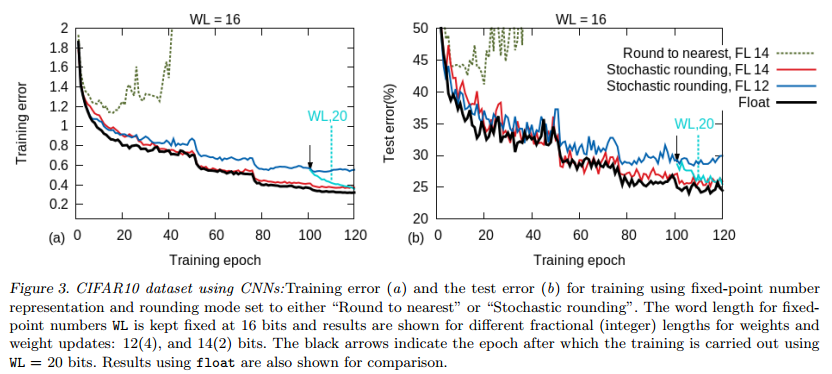
CIFAR-10
・training image 50,000, test image 10,000 RGB image 32x32
・input range [0,1]
・data augmentationなし
・3 convolutional layer
・5x5 fiter 64 feature maps
・max pooling 3x3 stride = 2
・learning rate 0.01 epoch 50, 75, 100 の時に1/2
Stochastic roundingだとFL=14でFloatingと同じぐらいの性能
Hardware Prototyping
Xilinx Kintex325T FPGA, 8 GB DDR3 memoryで実装したとのこと。
性能は37Giga ops/s/W (opsはoperations, Wはワット 1秒間1Wの時のOperation回数)
NVIDIA GT650m, GTX780だと1-5 G-ops/s/Wとのこと。
実装の詳細は論文参照してください。
最後に
Round to nearestに比べてStochastic roundingがいいのは、おそらく四捨五入の結果が確率的に変わるので値がRound to nearestよりは0になりにくいのがいいのでしょうか?
今だとNVIDIAのCUDAが16bit floating pointをサポートしているので、それと比較するとメモリの節約効果はあまり無い気がする。
ただ固定小数点と浮動小数点ではH/W Cost&演算速度が異なるので、そのへんはメリットがあるかも。
モデルごとに必要な精度が異なるのがネックになりそう。