Pythonで有界な（閉じた）ボロノイ図を計算・描画する

はじめに

Pythonでボロノイ図を計算・描画するライブラリとしては，scipy.spatial.Voronoiとscipy.spatial.voronoi_plot_2dが挙げられます．
これらについての詳細は，以下のサイトを参照してください．

• scipy.spatial.Voronoiの公式ドキュメント
• scipy.spatial.voronoi_plot_2dの公式ドキュメント
• [scipy Voronoi](https://qiita.com/kwi/items/4b7162fbada390501d06"scipy Voronoi")

ただし，これらのライブラリで作られるボロノイ図は，非有界な（閉じていない）空間上で計算されるので，外側のボロノイ辺やボロノイ領域（多角形）の情報を得ることができません．
そこで今回は，閉じた領域をボロノイ分割する方法を紹介します．

実装

ボロノイ領域を有界にする部分は，こちらの記事を参考にさせていただきました．
大まかな流れは以下の通りです．

1. すべてのボロノイ領域を有界にするために，ダミーの母点を3個追加する．
2. scipy.spatial.Voronoiでボロノイ図を計算する．
3. 分割する領域と各ボロノイ領域の共通部分をshapelyで計算する．
4. 3で求めた多角形を描画する．

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.collections import PolyCollection
from scipy.spatial import Voronoi, voronoi_plot_2d
from shapely.geometry import Polygon

def bounded_voronoi(bnd, pnts):
    """
    有界なボロノイ図を計算・描画する関数．
    """
    
    # すべての母点のボロノイ領域を有界にするために，ダミー母点を3個追加
    gn_pnts = np.concatenate([pnts, np.array([[100, 100], [100, -100], [-100, 0]])])
    
    # ボロノイ図の計算
    vor = Voronoi(gn_pnts)
    
    # 分割する領域をPolygonに
    bnd_poly = Polygon(bnd)
    
    # 各ボロノイ領域をしまうリスト
    vor_polys = []
    
    # ダミー以外の母点についての繰り返し
    for i in range(len(gn_pnts) - 3):
        
        # 閉空間を考慮しないボロノイ領域
        vor_poly = [vor.vertices[v] for v in vor.regions[vor.point_region[i]]]
        # 分割する領域をボロノイ領域の共通部分を計算
        i_cell = bnd_poly.intersection(Polygon(vor_poly))
        
        # 閉空間を考慮したボロノイ領域の頂点座標を格納
        vor_polys.append(list(i_cell.exterior.coords[:-1]))
    
    
    # ボロノイ図の描画
    fig = plt.figure(figsize=(7, 6))
    ax = fig.add_subplot(111)
    
    # 母点
    ax.scatter(pnts[:,0], pnts[:,1])
    
    # ボロノイ領域
    poly_vor = PolyCollection(vor_polys, edgecolor="black",
                              facecolors="None", linewidth = 1.0)
    ax.add_collection(poly_vor)
    
    xmin = np.min(bnd[:,0])
    xmax = np.max(bnd[:,0])
    ymin = np.min(bnd[:,1])
    ymax = np.max(bnd[:,1])
    
    ax.set_xlim(xmin-0.1, xmax+0.1)
    ax.set_ylim(ymin-0.1, ymax+0.1)
    ax.set_aspect('equal')
    
    plt.show()
    
    return vor_polys

単位正方形を分割

以上の関数を使って単位正方形を分割すると，次のようになります．

# ボロノイ分割する領域
bnd = np.array([[0, 0], [1, 0], [1, 1], [0, 1]])

# 母点の個数
n = 30
# 母点座標
pnts = np.random.rand(n, 2)

# ボロノイ図の計算・描画
vor_polys = bounded_voronoi(bnd, pnts)

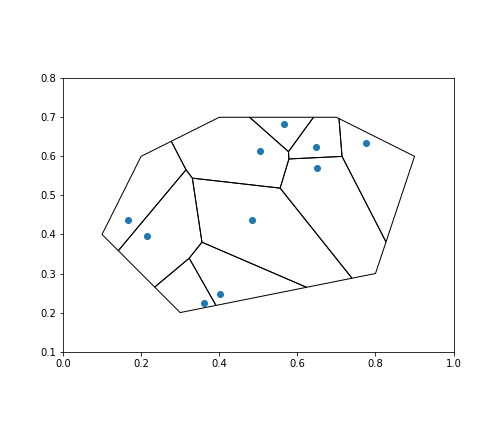
一般の凸多角形を分割

正方形ではない一般の凸多角形も同様に分割できます．

from scipy.spatial import ConvexHull

def points_in_convex_polygon(bnd, n):
    """
    凸多角形の内部にn個の点をランダムに発生させる関数．
    """
    
    #領域の境界を表す行列の作成
    bndhull = ConvexHull(bnd)
    bndTmp = bndhull.equations
    bndMat = np.matrix(bndTmp)
    Abnd = np.array(bndMat[:,0:2])
    bbnd = np.array(bndMat[:,2])
    
    # 領域を囲む長方形
    xmin = np.min(bnd[:,0])
    xmax = np.max(bnd[:,0])
    ymin = np.min(bnd[:,1])
    ymax = np.max(bnd[:,1])
    
    # 繰り返し用
    i = 0
    pnts = []
    
    while i < n:
        
        # 点を生成
        pnt = np.random.rand(2)
        pnt[0] = xmin + (xmax - xmin) * pnt[0]
        pnt[1] = ymin + (ymax - ymin) * pnt[1]
        
        # 点が凸多角形内にあれば
        if (np.round(np.dot(Abnd,pnt.transpose()),7) <= np.round(-bbnd.transpose(),7)).all():

            pnts.append(pnt.tolist())
            i += 1

    return np.array(pnts)


# ボロノイ分割する領域
bnd = np.array([[0.1,0.4],[0.3,0.2],[0.8,0.3],[0.9,0.6],[0.7,0.7],[0.4,0.7],[0.2,0.6]])

# 母点の個数
n = 10
# 母点座標
pnts = points_in_convex_polygon(bnd, n)

# ボロノイ図の計算・描画
vor_polys = bounded_voronoi(bnd, pnts)