この記事は ドワンゴ Advent Calendar 2024 15日目の記事です。
はじめに
最近は寒く暖房なしで過ごしづらいですよね⛄
リモートワークの際も(もちろんオフィスでも)、暖房をつけた部屋で仕事をすることが多いと思います。暖房をつけると換気をおろそかにしてしまい部屋の空気がこもってしまうこともしばしばあり、二酸化炭素濃度が高まり、頭がぼーっとしてきたり集中力が低下することもあります。
実際、建築物環境衛生管理基準によると居室において二酸化炭素含有量を1000ppm以下に保つことが求められています。二酸化炭素濃度が1000ppmを超えてくると悪影響が出てくるようですのでこれを超えないように換気していきたいですね。
この記事では、部屋の単位時間あたりの換気量と二酸化炭素濃度の関係を数値的なシミュレーションと解析的に解くことで、快適なリモートワーク環境のためにどの程度換気すれば良さそうなのか見ていきます。
実験に使ったコードは記事の終わりにつけているのでコピペして条件を変えて遊んでください!
目次
- はじめに
- 目次
- 扱う内容
- 部屋の二酸化炭素濃度の増減を微分方程式でモデリング
- 微分方程式を数値的に扱う
- 微分方程式を解析的に解く
- 1000ppm以下に保つにはどうすれば良いのか?
- まとめ
- We are hiring!
- 実験コード
扱う内容
この記事で扱う内容は以下の通りです。
- 部屋の二酸化炭素濃度の増減を微分方程式でモデリング
- 微分方程式を数値的に扱う(
scipy.integrate.odeint) - 微分方程式を解析的に解く(
sympy) - 1000ppm以下に保つにはどうすれば良いのかを考える
部屋の二酸化炭素濃度の増減を微分方程式でモデリング
部屋についての仮定
今回の記事では以下のような部屋を想定しています。皆さんの作業環境に近いでしょうか?
- おおよそ6畳の$12\ \mathrm{m}^2$の部屋(高さ$2.4 \ \mathrm{m}$)を想定
- 室内に二酸化炭素の発生源(1人)が存在
- 新鮮な外気と室内の空気は常時一定量が交換されている
- 室内には9時間連続で滞在する(8時間労働として休憩時間もずっと同じ部屋にいるのは健康的だろうか🤔)
- 本当は二酸化炭素の拡散を考えないといけないが瞬時に二酸化炭素は拡散するものとする(つまり部屋の中の二酸化炭素濃度は均一)
二酸化炭素濃度のモデル化
二酸化炭素濃度が時間とともにどのように変化していくのかを考えていきます。ここでは、二酸化炭素濃度に影響を与える要因についてまず定性的な考察をして、その考察を数式に落とし込んでいきます。
まず、部屋の二酸化炭素濃度がどのような原因によって増減するのかを考えてみましょう。先ほどの部屋についての仮定より、部屋には二酸化炭素の発生源(人間)があり、常時換気がなされているので増減の要因は3つに分解できそうです。
- 人間の呼吸によって生じる二酸化炭素
- 換気によって外に排出される二酸化炭素
- 換気によって外から流入してくる二酸化炭素
モデリングを行う前に、このモデル化で使う記号を以下のように定めておきます(二酸化炭素濃度を表すためにconcentrationsの$C$を使いたかったのですが、後に出てくる任意定数と名前が衝突しそうなためlevelの$L$としました)。
- $G$: 単位時間あたりの室内での二酸化炭素発生量
- $V_{room}$: 部屋の容積
- $A$: 部屋の単位時間あたりの換気量
- $t$: 入室からの経過時間
- $L_{0}$: 室内の二酸化炭素濃度の初期値
- $L_{outdoor}$: 外気の二酸化炭素濃度
- $L(t)$: ある時刻$t$における室内の二酸化炭素濃度
人間の呼吸によって生じる二酸化炭素の影響
まず、人間の呼吸の影響を考えましょう。人間が運動しているようなときには呼吸が激しくなり、時間あたりの二酸化炭素発生量$G$が大きくなるので部屋の二酸化炭素濃度が急激に上昇するでしょう。
また、広い部屋であるほど、すなわち部屋の容積$V_{room}$が大きければ大きいほど、人間の呼吸によって発生した二酸化炭素が部屋の二酸化炭素濃度に与える影響は小さくなるでしょう。
これを数式で表すと、二酸化炭素濃度の上昇速度は$\frac{G}{V_{room}}$と表現できます。
換気によって外に排出される二酸化炭素の影響
次に、換気による室外への排出の影響を考えましょう。換気扇を強く回したり、窓を大きく開けたりするときには空気がよく入れ替わり(つまり$A$が大きくなり)二酸化炭素はよく室外に排出されるでしょう。
また、部屋の二酸化炭素濃度$L(t)$が高ければ高いほど、ある量の空気を室外に排出したとき、その中に含まれている二酸化炭素の量が多くなるため、二酸化炭素はよく室外に排出されるでしょう。
二酸化炭素濃度を考えるうえで忘れてはならないのが、部屋の容積$V_{room}$の影響です。部屋が大きければ大きいほど、ある量の二酸化炭素を室外に排出したときの二酸化炭素濃度の下げ幅は小さくなってしまうことにも注意しなければなりません。
これを数式で表すと、室外への二酸化炭素排出による二酸化炭素濃度の上昇速度(不自然な言い方ですが)は$\frac{-AL(t)}{V_{room}}$と表現できます。
換気によって外から流入してくる二酸化炭素の影響
我々は地球に住んでいますから、外気中にも二酸化炭素は存在しています。外気の二酸化炭素濃度$L_{outdoor}$が高ければ高いほど、そして単位時間あたりの換気量$A$を大きくすればするほど二酸化炭素は多く流入してきます。また、部屋の容積$V_{room}$が大きければ大きいほど、流入してきた二酸化炭素が部屋の二酸化炭素濃度に与える影響は小さくなります。
これを数式で表すと、室内への二酸化炭素流入による二酸化炭素濃度の上昇速度は$\frac{AL_{outdoor}}{V_{room}}$と表現できます。
微分方程式によるモデリング
二酸化炭素の発生・流入・排出について見てきました。これらの結果をまとめることで部屋の二酸化炭素濃度について以下の微分方程式を立てることができます。
$$
\frac{\mathrm{d}L(t)}{\mathrm{d}t}=\frac{G}{V_{room}} - \frac{AL(t)}{V_{room}}+\frac{AL_{outdoor}}{V_{room}}
$$
微分方程式を数値的に扱う
ここでは scipy.integrate.odeint を使うことで上の微分方程式をもとに部屋の二酸化炭素濃度が時間経過とともにどのように変化していくのかを見ていきます。
まず、先ほどの微分方程式を関数 co2_level として表現します。
次に、この関数を使って部屋についての仮定に準じて定数を以下のように定めて、二酸化炭素濃度の推移を単位時間あたりの換気量を変えながらシミュレーションしていきます。
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
def co2_level(L, t, v_room, generation_rate, air_exchange_rate, L_outdoor):
"""
t: 経過時刻
L: ある時刻tにおける室内の二酸化炭素濃度L(t)
v_room: 部屋の容積
generation_rate: 時間あたりの二酸化炭素発生量
air_exchange_rate: 単位時間あたりの換気量
L_outdoor: 室外の二酸化炭素濃度
"""
dLdt = (
generation_rate / v_room
- air_exchange_rate * L / v_room
+ air_exchange_rate * L_outdoor / v_room
)
return dLdt
ROOM_VOLUME_LITTERS = (
11 * 2.4 * 10**3
) # 部屋が何リットルの容積であるか(六畳で高さ2.4 mの部屋を想定)
# 二酸化炭素が毎秒何リットル発生するか
# 人間は呼吸で1日に1 kgの二酸化炭素を出すらしい。
# 二酸化炭素の分子量が44であることと理想気体とみなして標準状態の1 molあたりの体積を考えると。だいたい0.006 L/sの二酸化炭素を人間は発生させていることになる
CO2_GENERATION_RATE_LPS = 0.006
OUTDOOR_CO2_LEVEL = 0.04 / 100 # 外気の二酸化炭素濃度 (e.g. 0.04% → 0.04 / 100)
INITIAL_CO2_LEVEL = (
0.04 / 100
) # 部屋の初期状態の二酸化炭素濃度 (e.g. 0.04% → 0.04 / 100)
TIME_SECONDS = np.linspace(
0, 60 * 60 * 9, 1000
) # 8時間労働で休憩時間も室内にいることを考えて9時間
AIR_EXCHANGE_RATES_LPS = [3, 5, 10, 20, 40] # 換気量(L/s)
# 換気量を変えたときにどのように室内の二酸化炭素濃度が移り変わっていくのかを可視化する。
plt.figure(figsize=(8, 5))
for air_exchange_rate_lps in AIR_EXCHANGE_RATES_LPS:
solution = odeint(
co2_level,
INITIAL_CO2_LEVEL,
TIME_SECONDS,
args=(
ROOM_VOLUME_LITTERS,
CO2_GENERATION_RATE_LPS,
air_exchange_rate_lps,
OUTDOOR_CO2_LEVEL,
),
)
co2_concentration_over_time = solution.flatten()
plt.plot(
TIME_SECONDS / 3600, # seconds → hours
co2_concentration_over_time * 10**6, # L/L → ppm
label=f"Air exchange rate = {air_exchange_rate_lps} L/s",
)
plt.xlabel("Time (hours)")
plt.ylabel("CO$_2$ concentration (ppm)")
plt.title(
"Time evolution of indoor CO$_2$ concentration for varying air exchange rates"
)
plt.legend()
plt.grid()
plt.show()
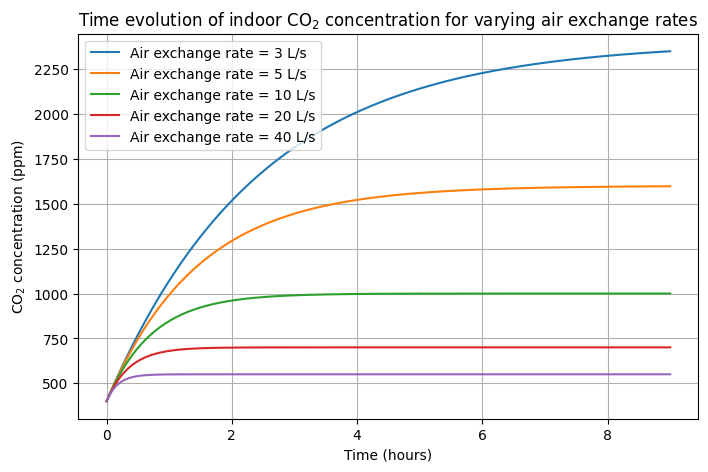
シミュレーション結果を見たところ、$10 \ \mathrm{L/s}$程度の換気で部屋の二酸化炭素濃度を1000ppm以下に保てそうなことがわかります。
また、二酸化炭素濃度の上昇が最初は急で、時間の経過とともに単位時間あたりの換気量に応じてある値(平衡濃度)に近づいていきそうなこと、平衡濃度は単位時間あたりの換気量を大きくすれば大きくするほど低くなりそうなことも見て取れます。これは、室内の二酸化炭素濃度が高くなれば高くなるほど一定量の空気を入れ替えたときの二酸化炭素の量の減少幅が大きくなり、「室内で発生する二酸化炭素の量+外気から流入してくる二酸化炭素の量」が「室外に排出される二酸化炭素の量」に近づいていき最終的にバランスされることに由来します。
微分方程式を解析的に解く
解析解を求める
数値解析で二酸化炭素濃度の挙動について把握できましたが、ある時刻$t$における二酸化炭素濃度$L(t)$がどのような数式で表現できるのかを求めることで、部屋の容積などが変わったときに二酸化炭素濃度がどのように変化していくのかをより直感的に把握できるようになります。ここでは$L(t)$がどのように表現できるのかを数式処理ライブラリである sympy を使って解析的に導きます。
やることはシンプルで、おおむね数値解析のときと同じ手順で微分方程式を ode = sp.Eq(L.diff(t), dLdt) と定義して解かせるだけです。
import sympy as sp
from IPython.display import display
t = sp.symbols("t")
L = sp.Function("C")(t)
V = sp.symbols("V_room", positive=True)
G = sp.symbols("G", positive=True)
Lo = sp.symbols("L_outdoor", positive=True)
A = sp.symbols("A", positive=True)
dLdt = (G / V) - (A / V) * L + (A / V) * Lo
ode = sp.Eq(L.diff(t), dLdt)
L_sol = sp.dsolve(ode, L)
display(L_sol)
この微分方程式を解いた結果$L(t)$が以下のようになることがわかりました。
$$
L{\left(t \right)} = C_{1} e^{- \frac{A t}{V_{room}}} + L_{outdoor} + \frac{G}{A}
$$
任意定数$C_{1}$が具体的に$L(t)$がどのようになるのかを知るために邪魔なので、$t=0$における二酸化炭素濃度$L_{0}$を考えることでより具体的な形に変形しましょう。sympyでは以下のように初期条件を与えることができます。
L0 = sp.symbols('L_0')
L_sol_with_ic = sp.dsolve(ode, L, ics={L.subs(t, 0): L0})
display(L_sol_with_ic)
この実行結果からある時刻$t$における二酸化炭素濃度は以下のように数式を使って表現できることがわかりました。
$$
L{\left(t \right)} = L_{outdoor} + \frac{G}{A} + \frac{\left(A L_{0} - A L_{outdoor} - G\right) e^{- \frac{A t}{V_{room}}}}{A}
$$
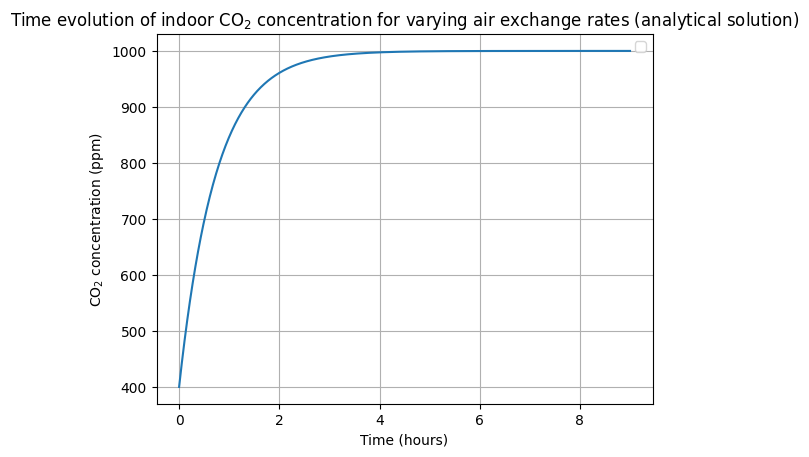
また、以下のコードを実行することで解析解と数値解析の結果が一致していることを確認できます。
params = {
G: CO2_GENERATION_RATE_LPS,
A: 10, # 10 L/sの換気を想定
L0: INITIAL_CO2_LEVEL,
Lo: OUTDOOR_CO2_LEVEL,
V: ROOM_VOLUME_LITTERS,
}
plt.plot(
TIME_SECONDS / 3600,
[L_sol_with_ic.rhs.subs(params).subs(t, i) * 10**6 for i in TIME_SECONDS],
)
plt.xlabel("Time (hours)")
plt.ylabel("CO$_2$ concentration (ppm)")
plt.title(
"Time evolution of indoor CO$_2$ concentration for varying air exchange rates (analytical solution)"
)
plt.legend()
plt.grid()
plt.show()
平衡濃度を考える
ここで数値解析の結果をもう一度見てみます。
数値解析のグラフを見るとある単位時間あたりの換気量のもと十分な時間が経過したときに二酸化炭素濃度がある一定の値に近づいているように見えました。また、単位時間あたりの換気量が大きければ大きいほどその値である平衡濃度が高くなるように見えました。
先ほど得られた以下の結果について$t$の無限大における極限を考えることで平衡濃度について考えていきましょう。
$$
L{\left(t \right)} = L_{outdoor} + \frac{G}{A} + \frac{\left(A L_{0} - A L_{outdoor} - G\right) e^{- \frac{A t}{V_{room}}}}{A}
$$
equilibrium_concentrations = sp.limit(L_sol_with_ic.rhs, t, sp.oo)
display(equilibrium_concentrations)
この実行結果から、無限に時間が経過したとき、最終的に部屋の二酸化炭素濃度は以下で安定することがわかります。
$$
L_{outdoor} + \frac{G}{A}
$$
かなりシンプルな形ですね。平衡濃度は外気の二酸化炭素濃度$L_{outdoor}$・時間あたりの室内での二酸化炭素発生量$G$・部屋の単位時間あたりの換気量$A$だけで定まり、部屋の容積$V_{room}$・初期濃度$L_{0}$は最終的な状態には寄与しないことがわかりました。
1000ppm以下に保つにはどうすれば良いのか?
求めた平衡濃度を求める式をもとに部屋の二酸化炭素濃度を1000ppm以下に保つためにはどの程度換気すれば良いのかを求めます。ここまでくれば手計算でも良い気がしますが、せっかくなのでsympyで解いてみます。
THRESHOLD = 1000 * 10 ** (-6)
inequality = equilibrium_concentrations <= THRESHOLD
CO2_GENERATION_RATE_LPS = 0.006
OUTDOOR_CO2_LEVEL = 0.04 / 100 # 外気の二酸化炭素濃度 (e.g. 0.04% → 0.04 / 100)
inequality_substituted = inequality.subs(
{Lo: OUTDOOR_CO2_LEVEL, G: CO2_GENERATION_RATE_LPS}
)
A_min = sp.solve_univariate_inequality(inequality_substituted, A, relational=True)
display(A_min)
このように表示されるはずです。
$$
10.0 \leq A
$$
この実行結果から、部屋の二酸化炭素濃度を1000ppm以下に保つためには、$10 \ \mathrm{L/s}$以上の換気の必要であることがわかりました。これは数値解析で出てきたグラフと整合性が取れてます。
最後に、$10 \ \mathrm{L/s}$すなわち$0.01 \ \mathrm{m^3/s}$の換気とはどの程度のものか簡単に見積もってみます。風量を空気の通過する面積で割ることで風速を算出できることに注意して、$20 \ \mathrm{cm}$四方の断面積$0.04 \ \mathrm{m^2}$の通風口を逆流などなしに空気が流れるものとします。
$$
\frac{0.01 \ \mathrm{m^3/s}}{0.04 \ \mathrm{m^2}} = 0.25 \ \mathrm{m/s}
$$
となることから、風速$0.25 \ \mathrm{m/s}$以上で$20 \ \mathrm{cm}$四方の通風口に風を通せば良いことがわかります。
まとめ
数値解析の結果から、ものすごく当然な結論ですが、単位時間あたりの換気量を上げれば上げるほど室内の二酸化炭素濃度を低く保てることがわかりました。
また、微分方程式の解析解から、条件が与えられたときの部屋の二酸化炭素濃度の推移を数式で表現し、最終的な部屋の二酸化炭素濃度は外気の二酸化炭素濃度・単位時間あたりの室内での二酸化炭素発生量・部屋の単位時間あたりの換気量だけで定まることがわかりました。
このように現実世界で起きている具体的な出来事について、妥当な仮定を置きながら問題を抽象化・一般化して数理的モデルで表現することで、ある妥当な仮定のもとでどのように物事が振る舞うのかを数理的に評価できます(あくまでも仮定のもとであることに注意は必要です)。このような考え方は、化学反応・交通・感染症のような種々の現象の理解や工学的な応用につなげられています。
寒い日が続きますが部屋の換気は欠かさないようにしましょう!
We are hiring!
株式会社ドワンゴの教育事業では、一緒に未来の当たり前の教育をつくるメンバーを募集しています。 カジュアル面談も行っています。 お気軽にご連絡ください!
開発チームの取り組み、教育事業の今後については、他の記事や採用資料をご覧ください。
実験コード
こちらのコードはコピペでGoogle ColabまたはJupyterLabを使って実行できます。Google Colabを使うとライブラリを新しくインストールする必要がなく楽です。
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
from scipy.integrate import odeint
from IPython.display import display
## 数値解析
def co2_level(L, t, v_room, generation_rate, air_exchange_rate, L_outdoor):
"""
t: 経過時刻
L: ある時刻tにおける室内の二酸化炭素濃度L(t)
v_room: 部屋の容積
generation_rate: 時間あたりの二酸化炭素発生量
air_exchange_rate: 単位時間あたりの換気量
L_outdoor: 室外の二酸化炭素濃度
"""
dLdt = (
generation_rate / v_room
- air_exchange_rate * L / v_room
+ air_exchange_rate * L_outdoor / v_room
)
return dLdt
ROOM_VOLUME_LITTERS = (
11 * 2.4 * 10**3
) # 部屋が何リットルの容積であるか(六畳で高さ2.4 mの部屋を想定)
# 二酸化炭素が毎秒何リットル発生するか
# 人間は呼吸で1日に1 kgの二酸化炭素を出すらしい。
# 二酸化炭素の分子量が44であることと理想気体とみなして標準状態の1 molあたりの体積を考えると。だいたい0.006 L/sの二酸化炭素を人間は発生させていることになる
CO2_GENERATION_RATE_LPS = 0.006
OUTDOOR_CO2_LEVEL = 0.04 / 100 # 外気の二酸化炭素濃度 (e.g. 0.04% → 0.04 / 100)
INITIAL_CO2_LEVEL = (
0.04 / 100
) # 部屋の初期状態の二酸化炭素濃度 (e.g. 0.04% → 0.04 / 100)
TIME_SECONDS = np.linspace(
0, 60 * 60 * 9, 1000
) # 8時間労働で休憩時間も室内にいることを考えて9時間
AIR_EXCHANGE_RATES_LPS = [3, 5, 10, 20, 40] # 換気量(L/s)
# 換気量を変えたときにどのように室内の二酸化炭素濃度が移り変わっていくのかを可視化する。
plt.figure(figsize=(8, 5))
for air_exchange_rate_lps in AIR_EXCHANGE_RATES_LPS:
solution = odeint(
co2_level,
INITIAL_CO2_LEVEL,
TIME_SECONDS,
args=(
ROOM_VOLUME_LITTERS,
CO2_GENERATION_RATE_LPS,
air_exchange_rate_lps,
OUTDOOR_CO2_LEVEL,
),
)
co2_concentration_over_time = solution.flatten()
plt.plot(
TIME_SECONDS / 3600, # seconds → hours
co2_concentration_over_time * 10**6, # L/L → ppm
label=f"Air exchange rate = {air_exchange_rate_lps} L/s",
)
plt.xlabel("Time (hours)")
plt.ylabel("CO$_2$ concentration (ppm)")
plt.title(
"Time evolution of indoor CO$_2$ concentration for varying air exchange rates"
)
plt.legend()
plt.grid()
plt.show()
## 解析解を求める
### 一般解を求める
t = sp.symbols("t")
L = sp.Function("C")(t)
V = sp.symbols("V_room", positive=True)
G = sp.symbols("G", positive=True)
Lo = sp.symbols("L_outdoor", positive=True)
A = sp.symbols("A", positive=True)
dLdt = (G / V) - (A / V) * L + (A / V) * Lo
ode = sp.Eq(L.diff(t), dLdt)
L_sol = sp.dsolve(ode, L)
display(L_sol)
### 初期条件を考える
L0 = sp.symbols("L_0")
L_sol_with_ic = sp.dsolve(ode, L, ics={L.subs(t, 0): L0})
display(L_sol_with_ic)
### 数値解析の結果と同じグラフになるのか確認
params = {
G: CO2_GENERATION_RATE_LPS,
A: 10, # 10 L/sの換気を想定
L0: INITIAL_CO2_LEVEL,
Lo: OUTDOOR_CO2_LEVEL,
V: ROOM_VOLUME_LITTERS,
}
plt.plot(
TIME_SECONDS / 3600,
[L_sol_with_ic.rhs.subs(params).subs(t, i) * 10**6 for i in TIME_SECONDS],
)
plt.xlabel("Time (hours)")
plt.ylabel("CO$_2$ concentration (ppm)")
plt.title(
"Time evolution of indoor CO$_2$ concentration for varying air exchange rates (analytical solution)"
)
plt.legend()
plt.grid()
plt.show()
### 平衡濃度を求める
equilibrium_concentrations = sp.limit(L_sol_with_ic.rhs, t, sp.oo)
display(equilibrium_concentrations)
## 1000ppm以下を保つ
THRESHOLD = 1000 * 10 ** (-6)
inequality = equilibrium_concentrations <= THRESHOLD
inequality_substituted = inequality.subs(
{Lo: OUTDOOR_CO2_LEVEL, G: CO2_GENERATION_RATE_LPS}
)
A_min = sp.solve_univariate_inequality(inequality_substituted, A, relational=True)
display(A_min)