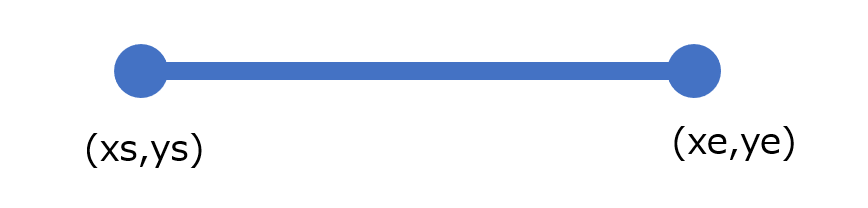SVGで簡単に矢印を描く方法: AI生成スクリプトの活用

はじめに

SVGの直線と三角形のオブジェクトで矢印を表現するスクリプトをつくるときに生成AIが便利だったので、それの紹介です。

SVGとは

SVG (Scalable Vector Graphics) は、HTML や XML を使用して定義される二次元のベクター画像形式です。
四角形や直線を数式で表現できるのでどんなに拡大しても画質が劣化しないという特徴があります。

作りたい矢印

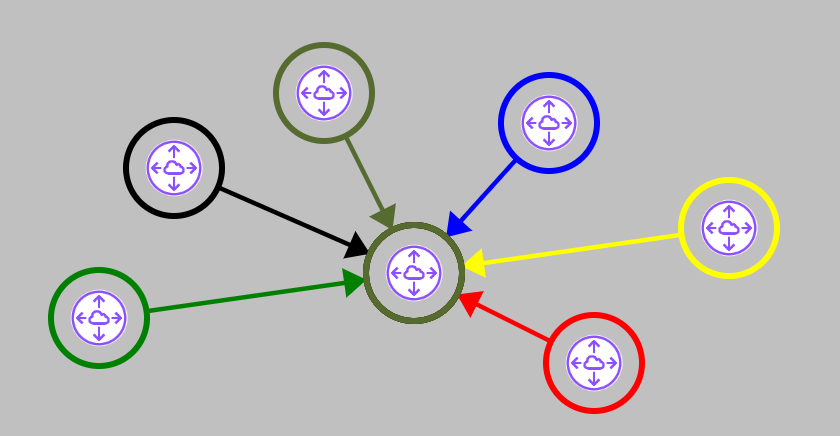
作りたい矢印はこんな感じです。

まずは直線を引きます。両終点の座標は任意の値が入るとします。

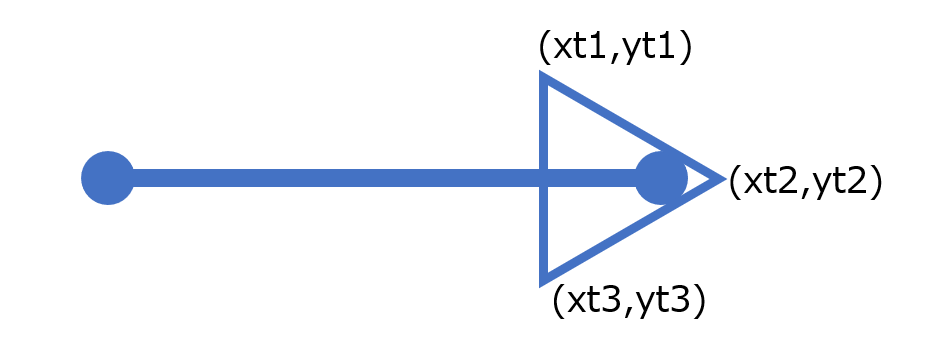
この直線に対し、三角形を矢印になるように描画します。SVGで三角形を描画するときに必要なのは3つの頂点の座標になります。この3つの頂点の座標を算出する計算式をスクリプトで作る必要があります。

できたもの

これが完成した矢印です。直線の座標がどのような値でも矢印の形になりました。

数式なので、以下の動画のように動的対応も可能です。

さわれるようにしました。雲アイコンをドラッグすると矢印の動きがわかります。

See the Pen gui-dac-矢印 by suo (@sosi-now) on CodePen.

作り方

三角形の座標を算出するスクリプトは生成AIに作ってもらいました。
ChatGTP(無料 GPT-4アーキテクチャ)に以下のプロンプトを入力し作成してもらいました。

直線と矢印の図形を使って矢印を描画したい。
直線の座標が(xs,ys),(xe,ye)とした場合、矢印となる三角形の座標(xt1,yt1),(xt2,yt2)(xt3,yt3)を算出するJavaScript関数を書いて

ChatGPTに作ってもらったスクリプトです。このスクリプトはエラーの発生せずそのまま使用しました。

function calculateArrowCoordinates(xs, ys, xe, ye) {
    // 矢印の長さと幅を設定
    const arrowLength = 10;
    const arrowWidth = 5;

    // 直線の方向ベクトルを求める
    const dx = xe - xs;
    const dy = ye - ys;
    const lineLength = Math.sqrt(dx * dx + dy * dy);

    // 矢印の方向ベクトルを正規化
    const ux = dx / lineLength;
    const uy = dy / lineLength;

    // 矢印の翼のベクトルを求める
    const vx = -uy * arrowWidth;
    const vy = ux * arrowWidth;

    // 三角形の頂点を計算
    const xt1 = xe;
    const yt1 = ye;
    const xt2 = xe - ux * arrowLength + vx;
    const yt2 = ye - uy * arrowLength + vy;
    const xt3 = xe - ux * arrowLength - vx;
    const yt3 = ye - uy * arrowLength - vy;

    return [
        { x: xt1, y: yt1 },
        { x: xt2, y: yt2 },
        { x: xt3, y: yt3 }
    ];
}

// 使用例
const xs = 50, ys = 50;
const xe = 100, ye = 100;
const arrowCoordinates = calculateArrowCoordinates(xs, ys, xe, ye);
console.log(arrowCoordinates);

---

以上でおわりです。

感想

"矢印にしたい"とこれしかプロンプトに書いてないのに意図を理解して期待通りのスクリプトを作ってくれる生成AIが素晴らしい。生成AIがなかったら、自分で数式考えて、それをスクリプトにしないといけなかったので超面倒だった。