chainer RNNで可変長ミニバッチの学習方法（波形分類）

chainerでRNNをしたい時に可変長のデータを学習するのってどうやるんだろうと思ったのでメモ。

結論から言うと、NStepLSTMを使うとできるようです。
ちょっと調べてみると、データの末尾-1埋めしてignore_label=-1とwhereを使うとか、長さ順にソートするとかめんどくさそうなことが色々出てきましたが、chainer(v1.16.0)以降ではそんなことをする必要は無くなったらしい。ありがたい。

NStepLSTMとは

NStepLSTMは、多層のLSTMを容易に定義できるモデルとなっており、かつ従来のLSTMに比べて高速に動作するようです。そして何より、ミニバッチのデータの長さをそろえる必要がなくなりました。

使い方

lstm = L.NStepLSTM(n_layers=1, in_size=10,
                      out_size=5, dropout=0.3)

n_layersはLSTMの層の数、in_sizeは入力ベクトルの次元数、out_sizeは出力ベクトル（及び隠れベクトル）の次元数です。

関数の入出力は以下のように行います。

xs = [
    Variable(np.random.rand(4, 10), 
    Variable(np.random.rand(5, 10),
    Variable(np.random.rand(6, 10)
]
hy, cy, ys = lstm(hx=None, cx=None, xs=xs_f)

xsで可変長のデータを3つ用意しています。lstmの引数であるhx, csはNoneを入れておけばゼロベクトルを用意してくれます。
ysがNStepLSTMの最終層のベクトルの各ステップのベクトルです。

実際にやってみる

問題設定

何番煎じだよという感じですが、sin波を予測することを考えようと思います。今回はただsin波の点を予測するのではなく、与えられた可変長の時系列がsin波(っぽい)かどうかを判定する2値分類問題にしたいと思います。

環境
- python 3.5.2
- chainer v2.1.0

データ

sin波にノイズを加えたものと、ただの乱数列を適当に用意します。

def dataset(total_size, test_size):
    x, y = [], []
    for i in range(total_size):
        if np.random.rand() <= 0.5:
            # 長さ 10 ~ 20のsin波
            _x = np.sin(np.arange(0, np.random.randint(10, 20)) + np.random.rand())
            # ノイズを付加
            _x += np.random.rand(len(_x)) * 0.05
            x.append(v(_x[:, np.newaxis]))
            y.append(np.array([1]))

        else:
            # 長さ 10 ~ 20の[0,1]の乱数列
            _x = np.random.rand(np.random.randint(10, 20))
            x.append(v(_x[:, np.newaxis]))
            y.append(np.array([0]))

    x_train = x[:-test_size]
    y_train = vi(y[:-test_size])
    x_test = x[-test_size:]
    y_test = vi(y[-test_size:])
    return x_train, x_test, y_train, y_test

クラスの定義

LSTMの層は1、ベクトルの次元数は5で、LSTMを通した後最後のベクトルにReLUを通して全結合層を一層追加してsigmoidを噛ませています。

import numpy as np
import chainer
from chainer import cuda, Function, gradient_check, report, training, utils, Variable
from chainer import datasets, iterators, optimizers, serializers
from chainer import Link, Chain, ChainList
import chainer.functions as F
import chainer.links as L
from chainer.training import extensions

def v(x):
    return Variable(np.asarray(x, dtype=np.float32))


def vi(x):
    return Variable(np.asarray(x, dtype=np.int32))


class RNN(Chain):
    def __init__(self):
        super(RNN, self).__init__()
        input_dim = 1
        hidden_dim = 5
        output_dim = 1

        with self.init_scope():
            self.lstm = L.NStepLSTM(n_layers=1, in_size=input_dim,
                      out_size=hidden_dim, dropout=0.3)
            self.l1 = L.Linear(hidden_dim, hidden_dim)
            self.l2 = L.Linear(hidden_dim, output_dim)

    def __call__(self, xs):
        """
        Parameters
        xs : list(Variable)

        """
        _, __, h = self.lstm(None, None, xs)
        h = v([_h[-1].data for _h in h])
        h = F.relu(self.l1(h))
        y = self.l2(h)
        return F.sigmoid(y)

学習

上記で作ったクラスとデータセットを用いて、学習を行なっていきます。今回は2値分類問題なので誤差関数にはsigmoid_cross_entropyを利用します。またoptimizerはRMSPropを用いています。

def forward(x, y, model):
    t = model(x)
    loss = F.sigmoid_cross_entropy(t, y)
    return loss

def train(max_epoch, train_size, valid_size):
    model = RNN()

    # train に1000サンプル、 testに1000サンプル使用
    x_train, x_test, y_train, y_test = dataset(train_size + valid_size, train_size)

    optimizer = optimizers.RMSprop(lr=0.03)
    optimizer.setup(model)

    early_stopping = 20
    min_valid_loss = 1e8
    min_epoch = 0

    train_loss, valid_loss = [], []

    for epoch in range(1, max_epoch):
        _y = model(x_test)
        y = _y.data
        y = np.array([1 - y, y], dtype='f').T[0]
        accuracy = F.accuracy(y, y_test.data.flatten()).data

        _train_loss = F.sigmoid_cross_entropy(model(x_train), y_train).data
        _valid_loss = F.sigmoid_cross_entropy(_y, y_test).data
        train_loss.append(_train_loss)
        valid_loss.append(_valid_loss)

        # valid_lossが20回連続で更新されなかった時点で学習を終了
        if min_valid_loss >= _valid_loss:
            min_valid_loss = _valid_loss
            min_epoch = epoch

        elif epoch - min_epoch >= early_stopping:
            break

        optimizer.update(forward, x_train, y_train, model)
        print('epoch: {} acc: {} loss: {} valid_loss: {}'.format(epoch, accuracy, _train_loss, _valid_loss))

    loss_plot(train_loss, valid_loss)
    serializers.save_npz('model.npz', model)


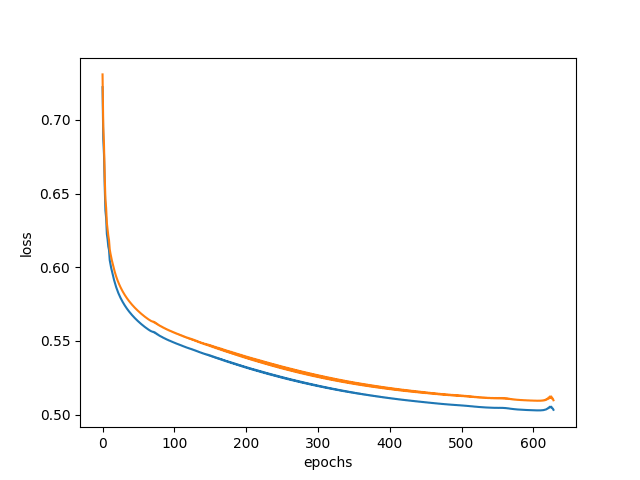
def loss_plot(train_loss, valid_loss):
    import matplotlib.pyplot as plt
    x = np.arange(len(train_loss))
    plt.plot(x, train_loss)
    plt.plot(x, valid_loss)
    plt.xlabel('epochs')
    plt.ylabel('loss')
    plt.savefig('loss.png')


if __name__ == '__main__':
    train(max_epoch=1000, train_size=1000, valid_size=1000)

結果

以下のような結果になりました。ほぼ100%の正解率を出しています。

epoch: 628 acc: 0.9990000128746033 loss: 0.5041547417640686 valid_loss: 0.5109608769416809

乱数列とsin列を入れてみます。出力が1に近いほどsin波っぽいことを表します。

In [36]: x = np.random.rand(15, 1)

In [37]: model([v(x)])
Out[37]: variable([[ 0.01768693]])

In [40]: x2 = np.sin(np.arange(0, 20)) + np.random.rand(20) * 0.1

In [41]: model([v(x2[:, np.newaxis])])
Out[41]: variable([[ 1.]])

確かにちゃんと予測できています。

In [56]: x2 = np.sin(np.arange(0, 20, 0.5)) + np.random.rand(40) * 0.5

In [57]: model([v(x2[:, np.newaxis])])
Out[57]: variable([[ 0.99997497]])

周期を変えてノイズを増やしてもほぼ1のままです。ロバスト。

まとめ

可変長のデータで学習の方法を学ぶということで、chainerのNStepLSTMを用いて簡単な波形の分類問題を解きました。

今度は実際の音声データなどで分類問題を解いてみたいなと思います。