はじめに
Microsoft の Kinect Azure などのデプス付きのRGB-Dカメラも普及していますが,近年,単眼カメラで人間の3次元姿勢を推定できる手法が発展しています.本記事では,RGB情報のみを用いた単眼カメラによる 3D Human Pose Estimationに関する,以下の論文について紹介します.
Coherent Reconstruction of Multiple Humans from a Single Image
CVPR 2020
Paper : https://arxiv.org/abs/2006.08586
Code : https://github.com/JiangWenPL/multiperson
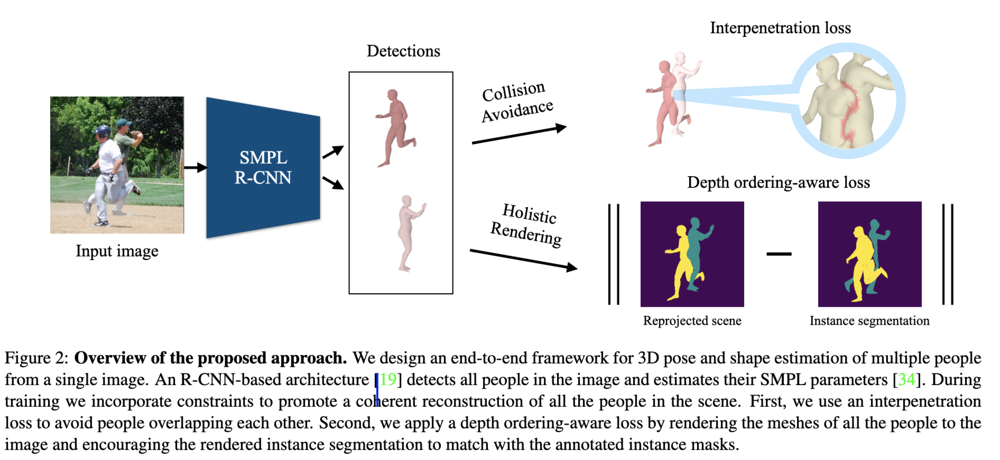
この論文を一言でいうと,画像中に複数人が映っているシーンにおいて,複数人の3次元姿勢の位置関係(接触 collision・前後 ordering)が正しくなるように,改善をした論文になります.
(論文の理解不足から誤った記述があるかもしれませんが,ご了承ください.)
論文のポイント
- 複数人推定した場合の Collision について,SMPL の Mesh からで算出した SDF をもとに Collision が発生しないようにする Interpenetration loss を提案.
- また,2D画像から検出した複数人の前後関係が,3D空間上でも正しくなるように,Depth ordering-aware loss も提案.
Architecture
R-CNNをベースの Human Mesh Recovery (HMR) を Baseline Architecture にしており,提案する Loss を加えて最適化しています.
End-to-end Recovery of Human Shape and Pose (CVPR2018)
Interpenetration loss
以下の論文にインスパイアされた Loss を提案しています.
Resolving 3D Human Pose Ambiguities with 3D Scene Constraints (ICCV2019)
先行研究では,SDF を用いた Penetration Loss という Loss が提案されています.

重なった人の Collision を計算するために,SDF をもとにして,人のMeshの内側に対してだけ負の距離,外側に対しては制約をかけないため 0 となるように,uSDF ($\phi$) を以下の式で求めます.
$$ \phi(x, y, z)=-\min (\operatorname{SDF}(x, y, z), 0) $$
uSDF で求められた $\phi$ を用いて,2人のPerson ( $i, j$ ) が Collision しないようにする関数を以下のように定義しています.
$$ \mathcal{P}_{i j}=\sum_{v \in M_{j}} \tilde{\phi}_{i}(v) $$
ここで,uSDF で求められた $\phi$ は,離散的な表現であるため,頂点 $v$ の座標をもとに線形補間してサンプリングして $\tilde{\phi}$ を計算しています.
しかしながら,Collisionが大きいシーンでは,平行移動に関する勾配が大きくなりすぎるため,Robust Estimator として,Geman-McClure ( $\rho$ ) を使い,複数人( $N$ )に対する Interpenetration loss を以下のように定義しています.
$$ L_{\mathcal{P}}=\sum_{j=1}^{N} \rho\left(\sum_{i=1, i \neq j }^{N} \mathcal{P}_{i j}\right) $$
Depth ordering-aware loss
2D画像から検出した複数人の前後関係が,3D空間上で一致するように,Loss を提案しています.
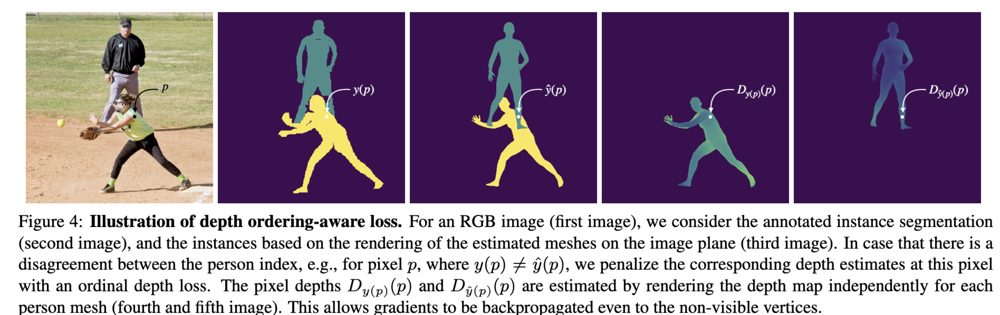
それぞれの Person に対して,SMPL のパラメータをもとに,Neural Mesh Rendering (NMR) でレンダリングして,Depth画像 ( $ D_i $ )を作成します.
Ground Truth と Depth を近づけるように,以下のように Depth ordering-aware loss を定義しています.
$$ L_{\mathcal{D}} =\sum_{p \in \mathcal{S}} \log \left(1+\exp \left(D_{y(p)}(p)-D_{\hat{y}(p)}(p)\right)\right) $$
ここで,集合 $\mathcal{S} ={p \in I: y(p)>0, \hat{y}(p)>0, y(p) \neq \hat{y}(p)}$ であり,各pixel ( $p$ )における person index の Ground Truth ( $y_p$ ) と 推定結果 ( $ \hat{y}(p)$ ) が一致しない pixel に対して,Loss を計算します.
ここで先行研究との大きな違いとして,先行研究では見える (visibleな) Person にしか Backpropagation できませんでした.これに対して提案手法では,一番手前の Occlusion がない Person だけでなく,どちらの人にも Mesh に対して,Backpropagation できます.
実験結果
Human3.6M データセットで,3D 関節座標(PA-MPJPE [mm])で評価した結果,従来手法のHMRベース手法と比較して,精度を上回っています.

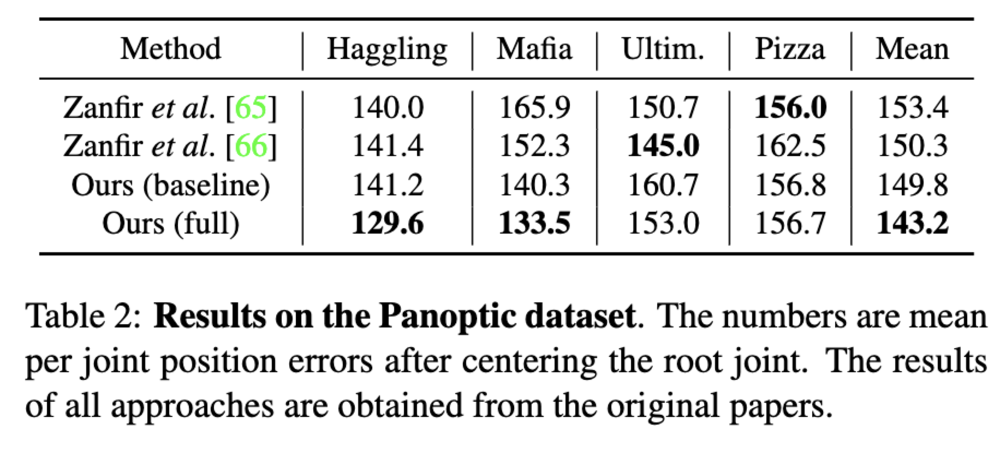
さらに,CMU Panoptic データセットに対しても,MPJPE[mm] で評価しています.結果として,SMPL で得られる Mesh から直接的な体積をを用いていない従来手法と比較して,各Protocol で精度を上回っています.
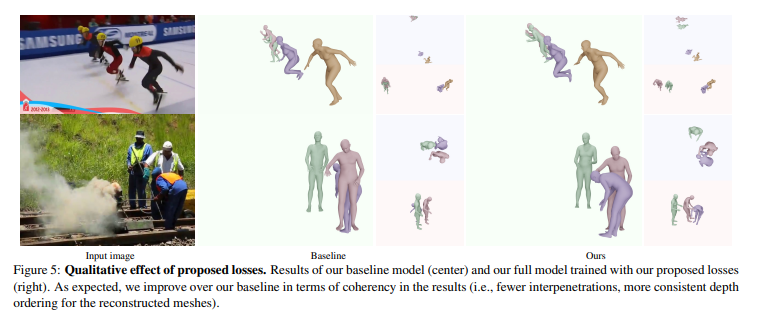
定性的な評価結果は,以下の通りで,3D空間上の人の位置関係が正しく求まることが示されています.
おわりに
- 従来手法では,SMPL で得られる Mesh に近くなるように,複数の3D球体を当てはめる手法が多く行われていたのに対して,SMPL の Mesh から直接的な変換に近い形で,Collision を表現できており,エレガントだと感じました.
- Geman-McClure の Robust Estimator を用いることは,時々他の研究でも行われていますが,どれだけ効果があるのか気になります.
参考文献
[1] Wen Jiang, et al. Coherent Reconstruction of Multiple Humans from a Single Image, CVPR2020
[2] Angjoo Kanazawa, et al. End-to-end Recovery of Human Shape and Pose, CVPR2018
[3] Mohamed Hassan, et al. Resolving 3D Human Pose Ambiguities with 3D Scene Constraints, ICCV2019