パーセプトロンとニューラルネットワークの違い
パーセプトロンの応用がニューラルネットワーク
具体的には、最終的な出力の活性化関数が異なる
| 活性化関数 | 伝達方法 | |
|---|---|---|
| パーセプトロン | ステップ関数 一択 |
ステップ関数 $ b + w_1 + x_1 + w_2$ が $0$ を超えたら1、それ以外は $0$ を出力 |
| ニューラルネットワーク | 目的によって使い分ける 例) 回帰:恒等関数 分類:ソフトマックス関数 |
$h(b + w_1 + x_1 + w_2) $ を出力 |
を採用している
ニューラルネットワークの概要図$

第1層目の活性化関数の1番目のニューロン の活性化関数 $h()$ の入力は $a_1$
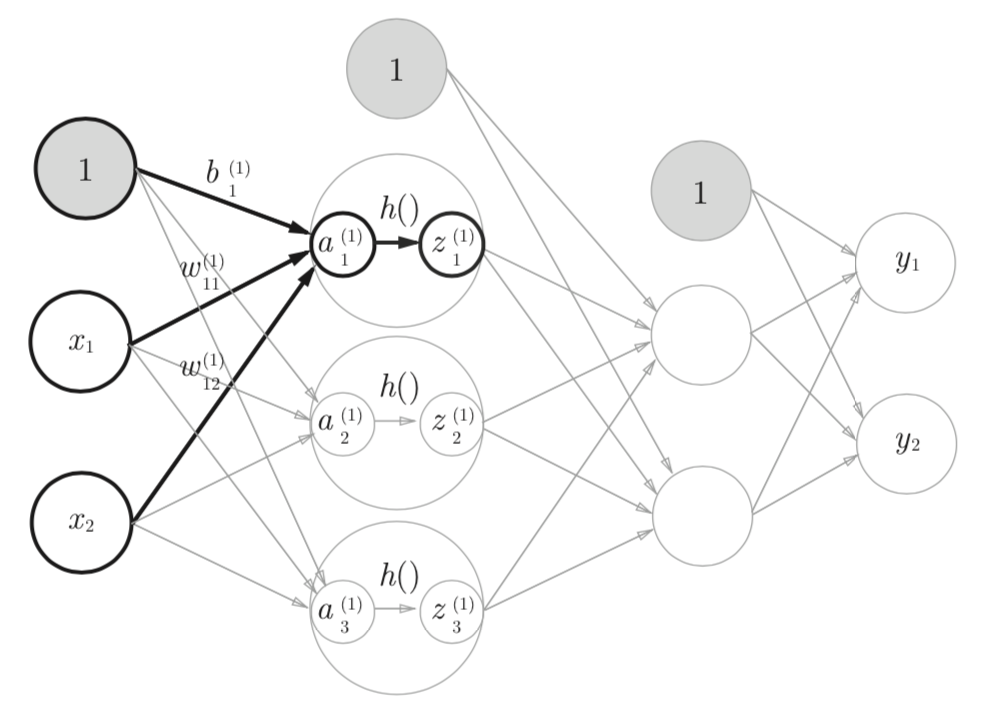
| 記号 | 意味 |
|---|---|
| X | 入力層 |
| $W^{(1)}$ | 1層目め重み |
| $B^{(1)}$ | 1層目のバイアス |
| $A^{(1)}$ | 1層目の重み付き和 |
| $h$ | 1層目の活性化関数 |
| $z^{(1)}$ | 1層目の活性化関数の出力 |
$$ A^{(1)} = XW^{(1)} + B^{(1)}$$
$$ Z^{(1)} = h(A^{(1)})$$

活性化関数
入力信号の総和
$$ 例: \ b + w_1 + x_1 + w_2 \ $$
を出力信号に変換する関数
$$ 例:h \ ( \ b + w_1 + x_1 + w_2 \ ) $$
を**活性化関数 ( activation function )**という
以下の活性化関数 $h(x)$ は入力が $0$ を超えたら $1$ を返し、そうでなければ $0$ を返す
\begin{align}
h \ (\ x \ )
&=
\begin{cases}
0 & ( \ x \leqq 0 \ ) \\
1 & ( \ x \gt 0 \ )
\end{cases}
\end{align}
多層ネットワークにおいて活性化関数に線形関数を用いると単層ネットワークで表現できるため、非線形関数を用いる
例)活性化関数 $$ h(x) = cx $$ である3層ネットワークを考えた場合
\begin{align}
y(x) &= h(h(h(x))) \\
&=cx \times cx \times cx \\
&=c^3 \times x
\end{align}
となり係数だけが異なる単層ネットワークの関数として表現できる為
恒等関数
入力値をそのまま出力する関数
回帰問題などで採用される
$$h \ (\ x \ ) = x $$

ステップ関数
閾値が考慮された入力値に対して、入力値が $0$ 以下ならば $0$、それ以外は $1$ を返却する
\begin{align}
h \ (\ x \ )
&=
\begin{cases}
0 & ( \ x \leqq 0 \ ) \\
1 & ( \ x \gt 0 \ )
\end{cases}
\end{align}
シグモイド関数 (sigmoid function)
ステップ関数に類似させた微分可能な関数
微分は勾配法によりパラメータを更新させる事が目的
$$
h \ ( x ) = \frac{1}{1 + e^{-x}}
$$
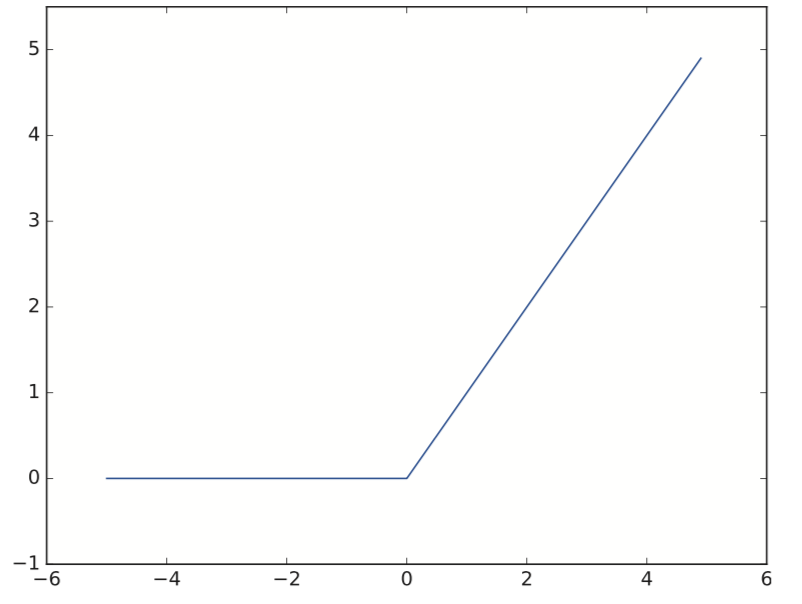
ReLU
入力が $0$ 以下であれば、$0$ を出力し、$0$ を超えていれば、その値を出力する関数
\begin{align}
h \ (\ x \ )
&=
\begin{cases}
0 & ( \ x \leqq 0 \ ) \\
x & ( \ x \gt 0 \ )
\end{cases}
\end{align}
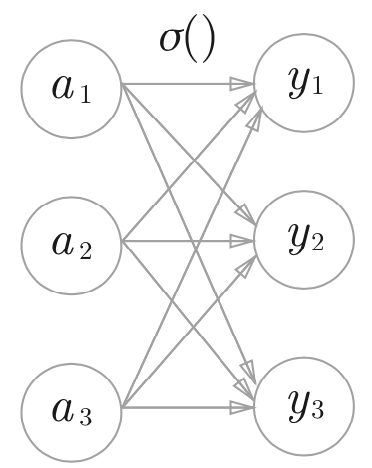
ソフトマックス
出力層が $n$ 個ある場合、$k$ 番目の出力 $y_k$ を求める場合
$$ y_k = \frac{e^{a_k}}{\displaystyle\sum_{i=1}^{n} e^{a_i}} $$
で定義される
但し、素で計算すると直ぐオーバーフローを起こしてしまう為
\begin{align}
y_k
&= \frac{e^{a_k}}{\displaystyle\sum_{i=1}^{n} e^{a_i}} \\\\
&= \frac{Ce^{a_k}}{C\displaystyle\sum_{i=1}^{n} e^{a_i}} \\\\
&= \frac{e^{a_k + logC}}{\displaystyle\sum_{i=1}^{n} e^{a_i + logC}} \\\\
&= \frac{e^{a_k + C'}}{\displaystyle\sum_{i=1}^{n} e^{a_i + C'}} \\\\
\end{align}
とする。但し
$ C=\max (e^{a_i}) \ (i = 1, 2, \cdots , n) \qquad C = e^{logC} \Longleftrightarrow log_e C = log_e e^{logC} $
各出力は、下記に示すように全ての入力から影響を受ける
$0〜1.0$ までの値を取り、総和は$1$であるので、確率とみなす事ができる