相関関係
2変数間の直線的な関係の事
一方の変数が増加する時、他方の変数も増加する傾向があるならば、正の相関関係
一方の変数が増加する時、他方の変数が減少する傾向があるならば、負の相関関係
があると言う
相関係数(correlation coefficient)
相関の程度を示す指標であり、一般にはピアソンの積率相関係数が使われる
$n$組みの2変数($x_i, y_i) \quad(i =1,2,・・・n)$ に対して相関係数$r_{xy}$は
\begin{align}
r_{xy} & = \frac{\frac{1}{n}\displaystyle\sum_{i=1}^{n}(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{\frac{1}{n}\displaystyle\sum_{i=1}^{n}(x_i-\overline{x})^2}\sqrt{\frac{1}{n}\displaystyle\sum_{i=1}^{n}(y_i-\overline{y})^2}} \\[5pt]
& = \frac{C_{xy}}{S_x S_y}\\[5pt]
& = \frac{\displaystyle\sum_{i=1}^{n}(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{\displaystyle\sum_{i=1}^{n}(x_i-\overline{x})^2}\sqrt{\displaystyle\sum_{i=1}^{n}(y_i-\overline{y})^2}}
\end{align}
と定義される。
但し
$\overline{x} = \displaystyle\sum_{i=1}^{n}x_i \quad\overline{y} = \displaystyle \sum_{i=1}^{n}y_i
$
$C_{xy}:共分散$、$S_x, S_y: x,yの標準偏差$
相関係数と因果関係
相関係数(correlation)と因果関係(causality)は異なる
例)身長と体重
相関関係とは2つのデータの直線的な関係のことであるが、因果関係は直線よりも複雑な関係も含まれる
例)$y=(x-8)^2$
(結果 $y$ は原因 $x$ の2次関数で表されるが、相関係数はゼロ)
みかけ上の相関
2つの変数AとB間には相関はないにも関わらず、A,Bと相関関係にある変数CによってA,B間にも相関があるように見えてしまう状態
例)飲食店が多いところは、金融機関も多い(p52)=> 相関係数 0.892
実際は、昼間人口数という変数が、飲食店数と金融機関数との間に相関がある
偏相関係数(partial correlation coefficient)
みかけ上の相関の対策として、偏相関係数 がある
変数1,2,3がある時、変数3の影響を除いた後に、変数1と変数2の間の相関係数を考えれば良い
$$
r_{12 \cdot 3} = \frac{r_{12}-r_{13}r_{23}}{\sqrt{1-r_{13}^2} \ \sqrt{1-r_{23}^2}}
$$
上式は次のように考える。
例えば、変数 $x$ ,$y$ $t$ の間に
$$ w_i = x_i + at_i \hspace{ 10pt }(1)$$
$$ z_i = y_i + bt_i \hspace{ 10pt }(2)$$
という関係があり、$x$ ,$y$の相関関係を知りたいとする。
この時、$z$の影響を除くと言うことは
$$ bw_i = bx_i + abt_i \hspace{ 10pt }(1)'$$
$$ az_i = ay_i + abt_i \hspace{ 10pt }(2)'$$
から
$$ bw_i - az_i = bx_i - ay_i (3)$$
$$ a\color{red}{y_i} = az_i - bw_i + b\color{red}{x_i}(3)'$$
と式変形して変数 $x$ ,$y$間の相関係数を求める事に他ならない
(導出は偏相関係数の意味と式の導出を参照)
層別と相関
全体では相関はないが、グループ分けした場合、相関が現れる事がある
順位相関係数
相関係数はデータがともに量的変数である場合に限られるが、2つの質的変数の相関を示す指標として スピアマンの定義とケンドールの定義によるものが使われる
両方とも順位が完全に一致している場合は +1 、完全に逆の場合は -1 となり
どの程度から相関があるかを判断する数値は簡約統計数値表で示されている
例)性別と好きな花の順位
| 桜 | 菊 | バラ | 梅 | ユリ | チューリップ | カーネーション | 椿 | |
|---|---|---|---|---|---|---|---|---|
| $R_{男}$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| $R_{女}$ | 3 | 1 | 2 | 5 | 4 | 7 | 6 | 8 |
今、男性のデータを$x_i$ 女性のデータを $y_i$ とすると
$ \overline{x} = \overline{y} = \frac{n+1}{2} $
$ \overline{x}^2 = \overline{y}^2 = \frac{(n+1)^2}{4} $
$ \displaystyle\sum_{i=1}^{n}x_i = \displaystyle\sum_{i=1}^{n}y_i =1 + 2 + \cdots + n = \frac{n(n+1)}{2} $
$ \displaystyle\sum_{i=1}^{n}x^2_i = \displaystyle\sum_{i=1}^{n}y^2_i =1^2 + 2^2 + \cdots + n^2 = \frac{n(n+1)(2n+1)}{6} $
を量的相関係数の式に当てはめたものがスピアマンの定義
$$ スピアマン \ r_s = 1 - \frac{6}{n^3 -n} \displaystyle\sum_{i=1}^{n}(R_i -R'_i)^2 $$
一方、ケンドールは $n$ 個の組み合わせデータ $(x_1, y_1), (x_2, y_2) \cdots (x_n, y_n)$を次のようにカウントする
| カウント | 条件1 | または | 条件2 | |
|---|---|---|---|---|
| 正順 G | +1 | $R_{男i} > R_{男j} \quad かつ \quad R_{女i} > R_{女j}$ | $ R_{男i} < R_{男j} \quad かつ \quad R_{女i} < R_{女j} $ | |
| 逆順 H | -1 | $R_{男i} > R_{男j} \quad かつ \quad R_{女i} < R_{女j}$ | $R_{男i} < R_{男j} \quad かつ \quad R_{女i} > R_{女j}$ |
$$ ケンドール \ r_K = \frac{G- H}{\frac{n(n-1)}{2}}$$
ここで、$ _nC_2 = \frac{n(n-1)}{2} $ は$n$この中から任意に2つピックアップしてくるパターン数
ケンドールの定義はどの程度、順位($Rank$)が離れているかは考慮しない。
あくまで順位の順序だけを見ており、同順位(タイ)があった場合は、一定の方式で修正(タイ修正)を行う事になっている
尚、ケンドールの順位相関係数を使って独立性の検定を行う事もできる
時系列
データが $x_1, x_2, \cdots , x_n $ が時間的に観測されたものである時、これらを時系列(time series)と呼ぶ
例)デーパートの毎月の売り上げ60ヶ月(n=60)
時系列データでは、番号の添え字が大きい程、未来のデータを表わす
現象の因果関係を調べようとする時、$i < j$ ならば $x_j$ は $x_i$ の結果と考えることは出来ても逆は考えられない
時間を表す添え字は分析時に強い制約を課す
自己相関係数(auto-correlation coefficient)
同じ観測対象 $x$ でも異時点間の相関係数を表すものを自己相関係数
例)遅れ=1の自己相関係数
| $x$ | $x_1$ | $x_2$ | $x_3$ | $\cdots$ | $\cdots$ | $x_{n-1}$ |
| $y$ | $x_2$ | $x_3$ | $x_4$ | $\cdots$ | $\cdots$ | $x_n$ |
$$ \overline{x} = \frac{(x_1 + x_2 + \cdots + x_{n})}{n}$$
とした場合
$$
r_1 = \frac{\displaystyle\sum_{i=1}^{n-1}\frac{(x_i-\overline{x})(x_{i+1} - \overline{x})}{n-1}}{\displaystyle\sum_{i=1}^{n}\frac{(x_i-\overline{x})^2}{n}}
= \frac{n}{n-1}\frac{\displaystyle\sum_{i=1}^{n-1}(x_i-\overline{x})(x_{i+1} - \overline{x})}{\displaystyle\sum_{i=1}^{n}(x_i-\overline{x})^2}
$$
を遅れ $lag1$ の自己相関係数 と呼ぶ
$r_1 < 0$ ならば、この時系列において各時点の傾向は1時点先には反転(数値が上昇していたならば、下降)する傾向がある事を示す
逆に$r_1 > 0$ ならば、1時点先も同じ傾向の持続がある事を示す
遅れ$h$の自己相関係数とは
$$
r_h = \frac{n}{n-h}\frac{\displaystyle\sum_{i=1}^{n-h}(x_i-\overline{x})(x_{i+h} - \overline{x})}{\displaystyle\sum_{i=1}^{n}(x_i-\overline{x})^2}
$$
の事であり、時間的隔たりの大きい2時点間の相関係数を見る事である
(年次など周期性を観る)
コレログラム(correlogram)
横軸が遅れ、縦軸が自己相関係数としてプロットしたもの
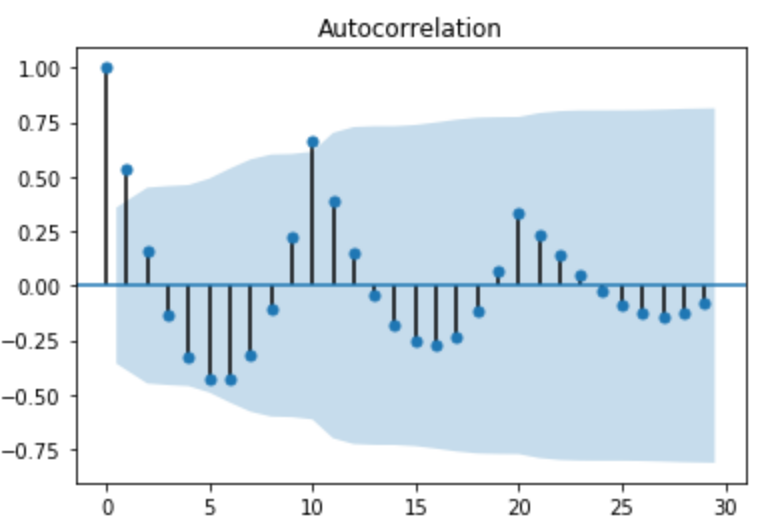
遅れ0とは時間差がない自分自身との相関であるため1
遅れ10、20で正の相関、遅れ5や15で負の相関が高くなっていると言うことは遅れ10の周期性があるデータである事を示している。
(グラフの青の帯は95%信頼区間)