sklearnのSpectralCoclusteringのアルゴリズムが数理的に面白かったのでまとめてみる。
元論文はこちら。
Dhillon, Inderjit S. (2001). "Co-clustering documents and words using bipartite spectral graph partitioning". Proceedings of the seventh ACM SIGKDD international conference on Knowledge discovery and data mining. pp. 269–274.
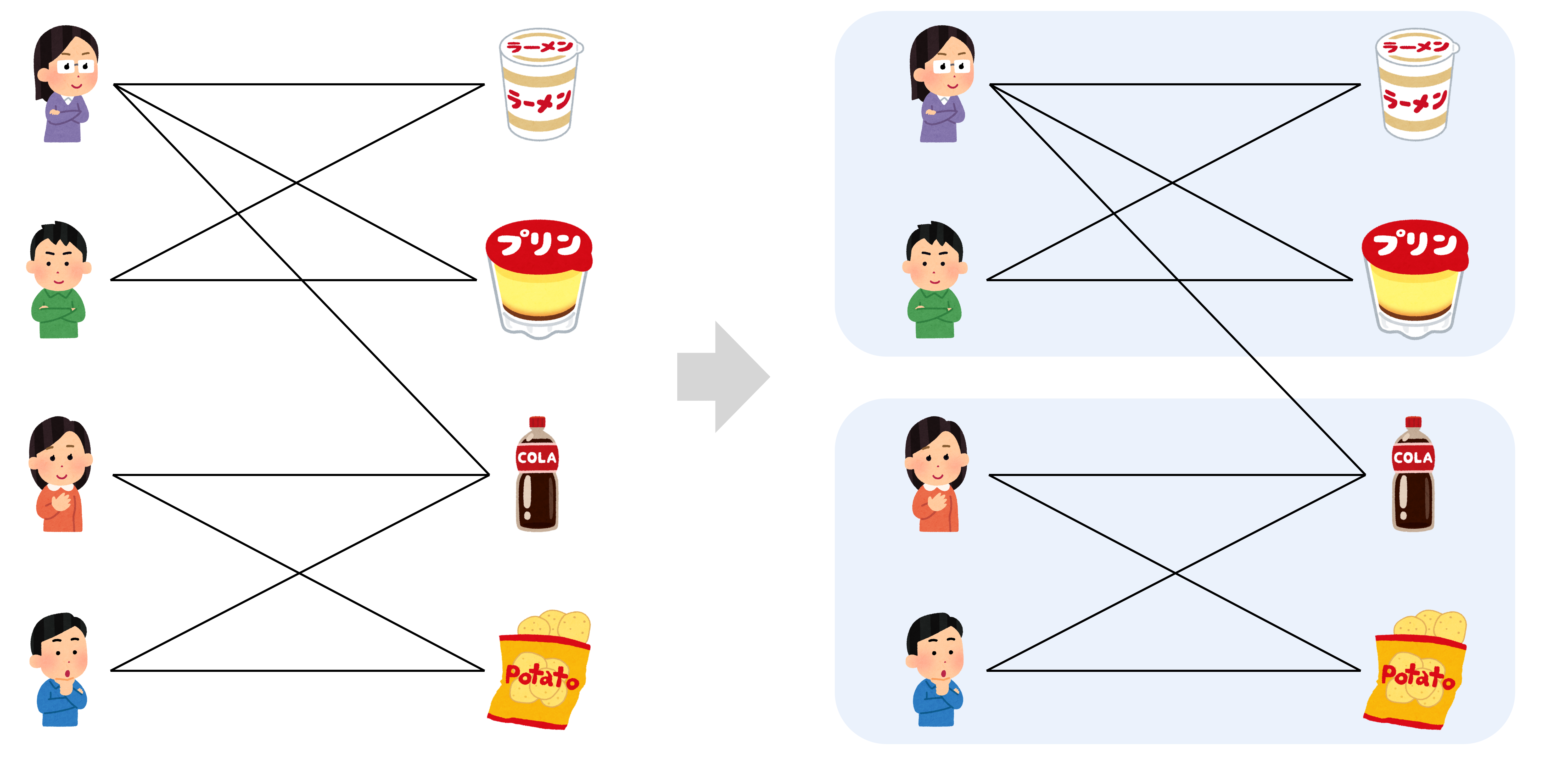
バイクラスタリング
バイクラスタリングは2つのオブジェクトの関係性に着目してクラスタリングを行う手法である。
例えば、ある店舗で顧客がどのような商品を購入したかというデータは、2部グラフで表現することができる。バイクラスタリングの目的は、この2部グラフを関係の近い顧客・商品のまとまりに分割することである。これにより相性の良い顧客・商品の組み合わせを抽出することができる。
バイクラスタリングは通常のクラスタリングと比較して、2つのオブジェクトのまとまりを同時にクラスタリングできるという点で嬉しさがある。
グラフの行列表記
データに対応する2部グラフを$G = (\mathcal{V}, E)$とし、2部グラフで表現される2つのオブジェクトそれぞれの頂点数を$m, n$とする(つまり$|\mathcal{V}| = m + n$)。
手法の説明にあたり、いくつか重要な行列を定義する。
2部グラフの行列表現を$A \in \mathbb{R}^{m \times n}$とする。
A_{ij} = \begin{cases}
1 \quad &(\{i,j\} \in E) \\
0 \quad &(\rm{otherwise})
\end{cases}
隣接行列を$M \in \mathbb{R}^{|\mathcal{V}| \times |\mathcal{V}|}$とする。2部グラフの構造から$M$は次のように書ける。
M = \begin{bmatrix}
\mathbf{0} & A \\
A^{T} & \mathbf{0}
\end{bmatrix}
次数行列、つまり各頂点の次数$\mathrm{deg}(v_i)$を並べた対角行列を$D \in \mathbb{R}^{|\mathcal{V}| \times |\mathcal{V}|}$とする。$D$の中で各オブジェクトに対応する小行列をそれぞれ$D_1, D_2$とする。
D = \begin{bmatrix}
D_1 & \mathbf{0} \\
\mathbf{0} & D_2
\end{bmatrix}
最後にラプラシアン行列を$L \in \mathbb{R}^{|\mathcal{V}| \times |\mathcal{V}|}$とする。ラプラシアン行列は対角成分には各頂点の次数、非対角成分には辺が存在する場合は-1、それ以外は0が入るような行列である。
L = D - M = \begin{cases}
\mathrm{deg}(v_i) \quad &(i = j) \\
-1 \quad &(i \neq j \ \mathrm{and} \ \{i, j\} \in E) \\
0 \quad &(\rm{otherwise})
\end{cases}
アルゴリズム
分割するクラスタの数を$k$とする。
1.データ行列$A$に対して頂点の次数でスケーリングした行列$A_n = D_1^{-1/2} A D_2^{-1/2}$を求める。
2.$A_n$の第2特異ベクトル以降の$l = \lceil \log_2 k \rceil$個の特異ベクトル
U = [u_2, \dots, u_{l+1}], \quad V = [v_2, \dots, v_{l+1}]
をもとに各頂点ごとの$l$次元ベクトル
Z = \begin{bmatrix}
D_1^{-1/2} U \\
D_2^{-1/2} V
\end{bmatrix} \in \mathbb{R}^{|\mathcal{V}| \times l}
を求める。
3.$Z$をもとにk-meansで頂点を$k$つの集合にクラスタリングする。
数理的背景
2部グラフの分割の問題がなぜ特異値分解に帰着されるのか、以下ではその数理的な背景について見ていく。
まず簡単のためクラスタ数を2とする。
問題の定式化
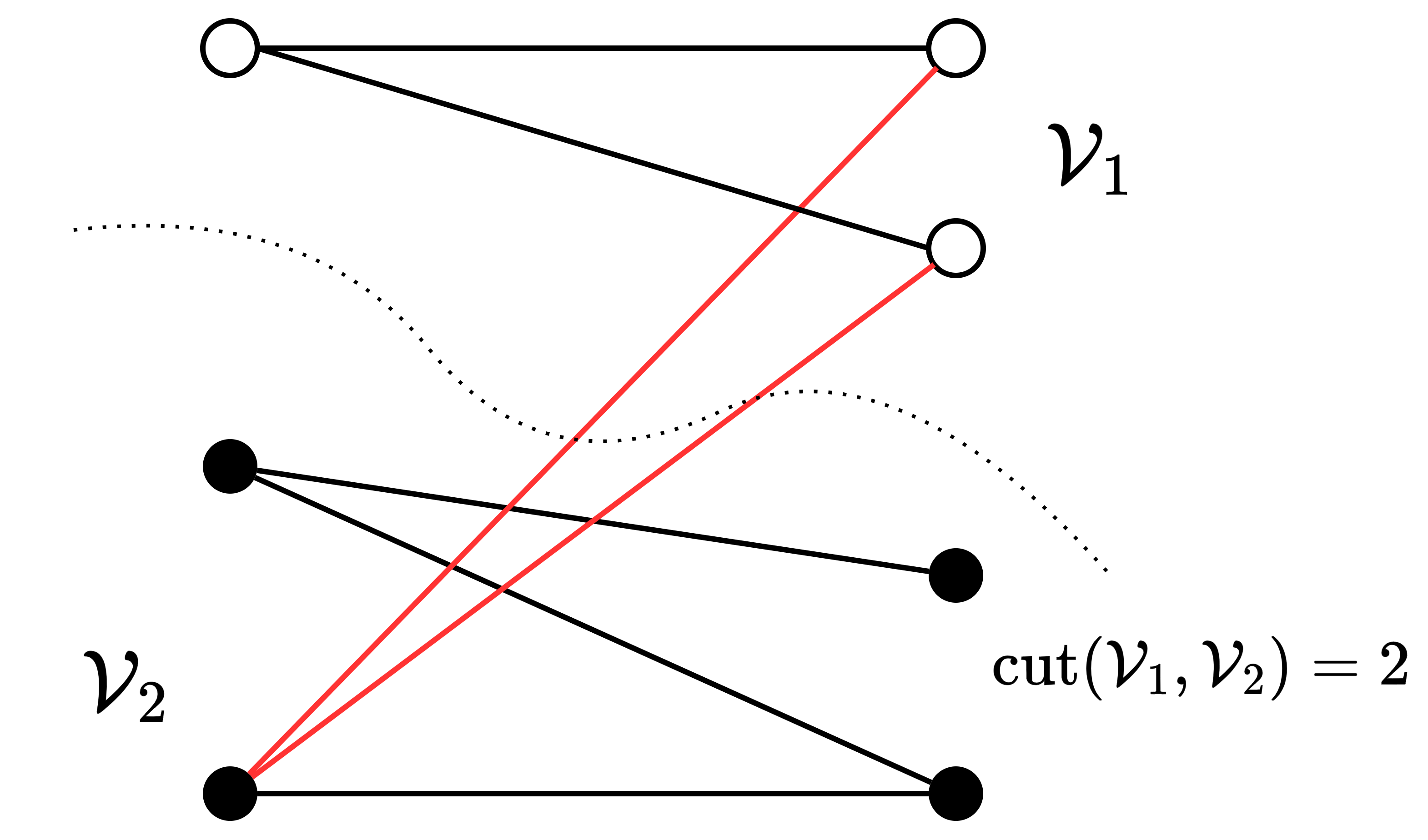
バイクラスタリングではグラフの最小カット問題を解くことで最適な頂点の分割を見つける。
カットとは頂点集合$\mathcal{V}$の分割$\mathcal{V}_1, \mathcal{V}_2$のことであり、$\mathcal{V}_1$と$\mathcal{V}_2$の間に接続された辺の本数をカットのサイズと呼ぶ。
\mathrm{cut}(\mathcal{V}_1, \mathcal{V}_2) = \sum_{i \in \mathcal{V}_1, j \in \mathcal{V}_2} M_{ij}
クラスタリングを行う上では、カットのサイズが小さいほど望ましいと考えられる。ただし、単にサイズの小さいカットを求めると、偏ったクラスタが得られる可能性がある。そこで、クラスタ同士のバランスを考慮した次の目的関数を最小化することを目標とする。
\mathcal{Q}(\mathcal{V}_1, \mathcal{V}_2) = \frac{\rm{cut}(\mathcal{V}_1, \mathcal{V}_2)}{\eta_1} + \frac{\rm{cut}(\mathcal{V}_1, \mathcal{V}_2)}{\eta_2}
ここで、$\eta_l$は頂点集合に含まれる頂点の次数の合計$\sum_{i \in V_l} \mathrm{deg}(v_i)$である。
実はこの目的関数は、ベクトル$z \in \mathbb{R}^{|\mathcal{V}|}$
z_i = \begin{cases}
+ \sqrt{\eta_2 / \eta_1} \quad &(i \in \mathcal{V}_1) \\
- \sqrt{\eta_1 / \eta_2}\quad &(i \in \mathcal{V}_2)
\end{cases}
を用いると、次のように行列を用いて簡潔に表現できる1。
\mathcal{Q}(\mathcal{V}_1, \mathcal{V}_2) = \frac{z^{T} L z}{z^{T} D z}
したがって、バランスを考慮した最小化カットを求める問題は、次のような最適化問題として定式化することができる。
\min_z \frac{z^{T} L z}{z^{T} D z} \quad \mathrm{s.t.} \ z_i \in \left\{ +\sqrt{\eta_2 / \eta_1}, \
-\sqrt{\eta_1 / \eta_2} \right\}
緩和問題と一般化固有値問題
$z$は2値ベクトルなので本質的には整数計画問題であり、一般には解くのが困難である。そこで、次の緩和問題を考える。
\min_{z \in \mathbb{R}^{|\mathcal{V}|} \setminus \mathbf{0}} \frac{z^T L z}{z^T D z}
この問題はよく知られているように、次の一般化固有値問題に帰着し、最小固有値とその固有ベクトルがそれぞれ最適値、最適解に対応する2。
Lz = \lambda D z
実は今回の設定においては、最小固有値は$\lambda = 0$、その固有ベクトルは$z \propto \mathbf{1}$となるが、これは全ての頂点を同一のクラスタに割り当てるナンセンスな解である。したがって実際に求めたいものは、0を除いた2番目に小さい固有値とその固有ベクトルとなる。
まとめると、グラフの最小カット問題は、緩和問題を通してラプラシアン行列の2番目に小さい固有値を求める問題に帰着する。このように、グラフのラプラシアン行列の固有ベクトルを利用してクラスタリングを行う手法を一般にスペクトラルクラスタリングと呼ぶ。
2部グラフと特異値分解
ここまでの話はグラフが2部グラフであるという情報を利用していないスペクトラルクラスタリングに関する一般的な結果である。ここから2部グラフの構造を利用することで、バイクラスタリングにおいて解くべき問題が最終的に特異値分解に帰着することを見る。
2部グラフにおいて次数行列、ラプラシアン行列がそれぞれ
D = \begin{bmatrix}
D_1 & \mathbf{0} \\
\mathbf{0} & D_2
\end{bmatrix}, \quad
L = \begin{bmatrix}
D_1 & -A \\
-A^{T} & D_2
\end{bmatrix}
と書けることを思い出すと、上記の一般化固有値問題は次のように書き下せる(固有ベクトルを$z = [x^T, y^T]^T$と置いた)。
\begin{align*}
D_1^{-1/2} A y &= (1 - \lambda) D_1^{1/2} x, \\
D_2^{-1/2} A^T x &= (1 - \lambda) D_2^{1/2} y
\end{align*}
これに対して
u = D_1^{1/2} x, \quad v = D_2^{1/2} y, \quad A_n = D_1^{-1/2} A D_2^{-1/2}, \quad \sigma = 1 - \lambda
と置くと、解くべき問題は結局以下の式で表すことができる。
A_n v = \sigma u, \quad A_n^{T} u = \sigma v
これはまさに特異値分解の式である。したがって、$\sigma = 1 - \lambda$の関係に注意すると、一般化固有値問題の2番目に小さい固有値とその固有ベクトルを求めることは、データ行列$A$を頂点の次数に応じてスケーリングした行列$A_n$に対して特異値分解を行い、第2特異値と第2特異ベクトルを求めることに相当する。
$A_n$は$L$よりも行列としてのサイズが小さいため、特異値分解として解くことは計算量の観点から嬉しさがある。
解の離散化
以上、バイクラスタリングにおけるグラフの最小カットを求める問題の緩和問題が、行列の第2特異ベクトルを求める問題に帰着することを見た。
第2特異ベクトル$u_2, v_2$が得られると、そこから以下のように緩和問題の最適解を復元できる。
z_2 = \begin{bmatrix}
D_1^{-1/2} u_2 \\
D_2^{-1/2} v_2
\end{bmatrix} \in \mathbb{R}^{|\mathcal{V}|}
これはあくまで緩和問題を解いて得られた実数ベクトルであるため、最終的なクラスタリングのためには、これを2値ベクトルに変換することを通して頂点を2つの集合に分割する必要がある。いくつかのアプローチが考えられるが、例えばk-means($k=2$)を用いることで、1次元データをもとに2つのクラスタに分離することができる。
手続きのまとめ
以上をまとめると、クラスタ数2の場合のバイクラスタリングの手続きは次のようになる。
- データ行列$A$に対して頂点の次数でスケーリングした行列$A_n = D_1^{-1/2} A D_2^{-1/2}$を求める。
- $A_n$の第2特異ベクトル$u_2, v_2$から緩和問題の解$z_2$を構成する。
- $z_2$に対してk-means($k=2$)を適用して最終的なクラスタリング結果を得る。
以上では簡単のためにクラスタ数が2の場合を考えたが、一般の$k$の場合でも基本的な考え方は同様である。クラスタ数が2の時に1本の特異ベクトル(第2特異ベクトル)を取ってきたところを、クラスタ数が$k$の時には$l = \lceil \log_2 k \rceil$本の特異ベクトルを取ってくる。
U = [u_2, \dots, u_{l+1}], \quad V = [v_2, \dots, v_{l+1}]
そして、各頂点に対応して得られる$l$次元ベクトル
Z = \begin{bmatrix}
D_1^{-1/2} U \\
D_2^{-1/2} V
\end{bmatrix} \in \mathbb{R}^{|\mathcal{V}| \times l}
をk-meansにかけることで頂点を$k$個のクラスタに分割する。
クラスタ数が$k>2$の場合には、$k=2$の時のような「グラフの最小カット問題の緩和問題を解く」というような直接的な解釈はできないと思われる(私見)が、経験的にはうまく機能するようだ。
まとめ
- グラフをベースとしたクラスタリングの問題は最小カット問題として定式化される。
- 最小カット問題の緩和問題はグラフのラプラシアン行列に対する(一般化)固有値問題に帰着する。
- バイクラスタリングにおける2部グラフの構造を利用すると、緩和問題は最終的にはデータ行列に対する特異値分解に帰着する。
2部グラフと特異値分解という一見関係の薄い対象が、バイクラスタリングを通してつながって見えるのが面白い。