因果推論と因果探索を学びたい初心者の方を対象に、因果分析のPythonプログラムを実際にGoogle Colaboratoryで実装しながら学ぶ書籍を執筆しました。
単著としては、「つくりながら学ぶ! PyTorchによる発展ディープラーニング」、以来、約1年ぶりの新刊となります。
本記事では、因果分析の書籍を執筆したモチベーション、Pythonによる因果推論、因果探索の概要について解説します。
「つくりながら学ぶ! Pythonによる因果分析 ~因果推論・因果探索の実践入門」
●2020年6月30日発売
●著者:小川雄太郎(自己紹介、[Twitter] (https://twitter.com/ISID_AI_team))@電通国際情報サービス(ISID)
●出版社: マイナビ出版
本記事の内容
● 0. 本書を執筆したモチベーション
● 1. 因果推論が必要な事例
● 2. 因果推論をしたいデータ
● 3. 因果推論の方法
● 4. 因果探索の手法
● 5. ディープラーニング × 因果探索
0. 本書を執筆したモチベーション
最近ではDXが流行りの言葉となり、ビジネスのデジタル化、そして、データ駆動型ビジネス実践の重要性がますます向上しています。
それにともない、データ駆動型ビジネスの各種施策を実施した結果を分析し、その効果をきちんと検証する必要があります。
そこで因果推論が必要になってきます。
しかしながら(私の実感では)、
-
因果推論と因果探索を両方扱っている本がない(少ない)
-
因果推論の分析プログラムをPythonで実装・解説してくれる、初心者向けの本がない
(少ない、とくにビジネスパーソン向け) -
因果探索の分野ではベイジアンネットワークも気になるが、因果探索本でベイジアンネットワークも一緒に説明してくれている本がない(少ない)
-
機械学習・ディープラーニングを使った最近の因果推論・因果探索の分析方法を解説してくれている本がない(少ない)
と、感じました(あくまで私の主観ですが)。
1冊で因果推論・因果探索がある程度理解でき、Pythonでの実装・分析まで解析してる入門書がないな~
それでは自分で書こう!と思ったのが、本書を執筆したモチベーションとなります。
1. 因果推論が必要な事例
本書籍、つくりながら学ぶ! Pythonによる因果分析 ~因果推論・因果探索の実践入門、の内容を抜粋しながら、因果推論・因果探索について解説します。
はじめに因果推論が必要となる架空事例を紹介します。
あなたは、企業に勤めており、人事部の部長として働いています。
社員研修の実施を担当するAさんから、
部下を持つ社員のうち、参加を希望した社員全員に実施した
「上司向け:部下とのキャリア面談のポイント研修」
の研修実施効果について報告を受けています。
期待する効果は、この研修を受けた上司が部下と良いキャリア面談を実施できるようになり、
部下社員のキャリア面談に対する満足度が向上することです。
Aさんからは具体的に以下のような報告を受けました。
-
部下社員(上司が、上記のキャリア面談のポイント研修を受講)と、部下社員(上司が研修を未受講)の中から、ランダムに100名ずつを抽出し、【キャリア面談の満足度】をアンケート調査しました
-
各100名ずつの【キャリア面談の満足度】の平均を計算した結果、上司が本研修を受講した社員の満足度平均値は、上司が研修を受けていない社員の満足度平均値よりも高い値となりました
-
今回アンケート調査を実施した部下社員100名ずつはランダムに抽出しています。異なる点は上司が研修を受けたか否かのみです
-
よって「上司向け:部下とのキャリア面談のポイント研修」は、部下のキャリア面談の満足度を向上させる効果があります
-
なお、研修実施による効果の大きさは、今回調査した部下の【キャリア面談の満足度】の平均値の差となります
以上が、部下のAさんから受けた報告です。
このように報告を受けたあなたは、違和感を覚えるかと思います。
そして次のような会話が続くでしょう。
「Aさん、研修の実施、そして効果検証までありがとう。ただ気になることがあるんだ。
研修を受講したことによる【当該社員の部下のキャリア面談の満足度】への効果を検証しているんだよね。
確認するが、今回の研修は参加希望者を募って、参加を希望した上司社員全員に実施したんだね?」
「はい。」
「う~ん・・・
わざわざ、この**「上司向け:部下とのキャリア面談のポイント研修」を自ら希望して受講する上司は、
そもそも【部下育成の熱心さ】**が高い上司だと思う。
そんな部下育成に熱心な上司を持つ社員なら、“もし仮にその上司が今回の研修を受けていなくても”、
その部下の**【キャリア面談の満足度】**は、研修を受講していない上司を持つ部下の満足度より高くなる気がするんだ。」
・・・
おそらく、このような会話が展開されるかと思います。
● 因果推論に向けて
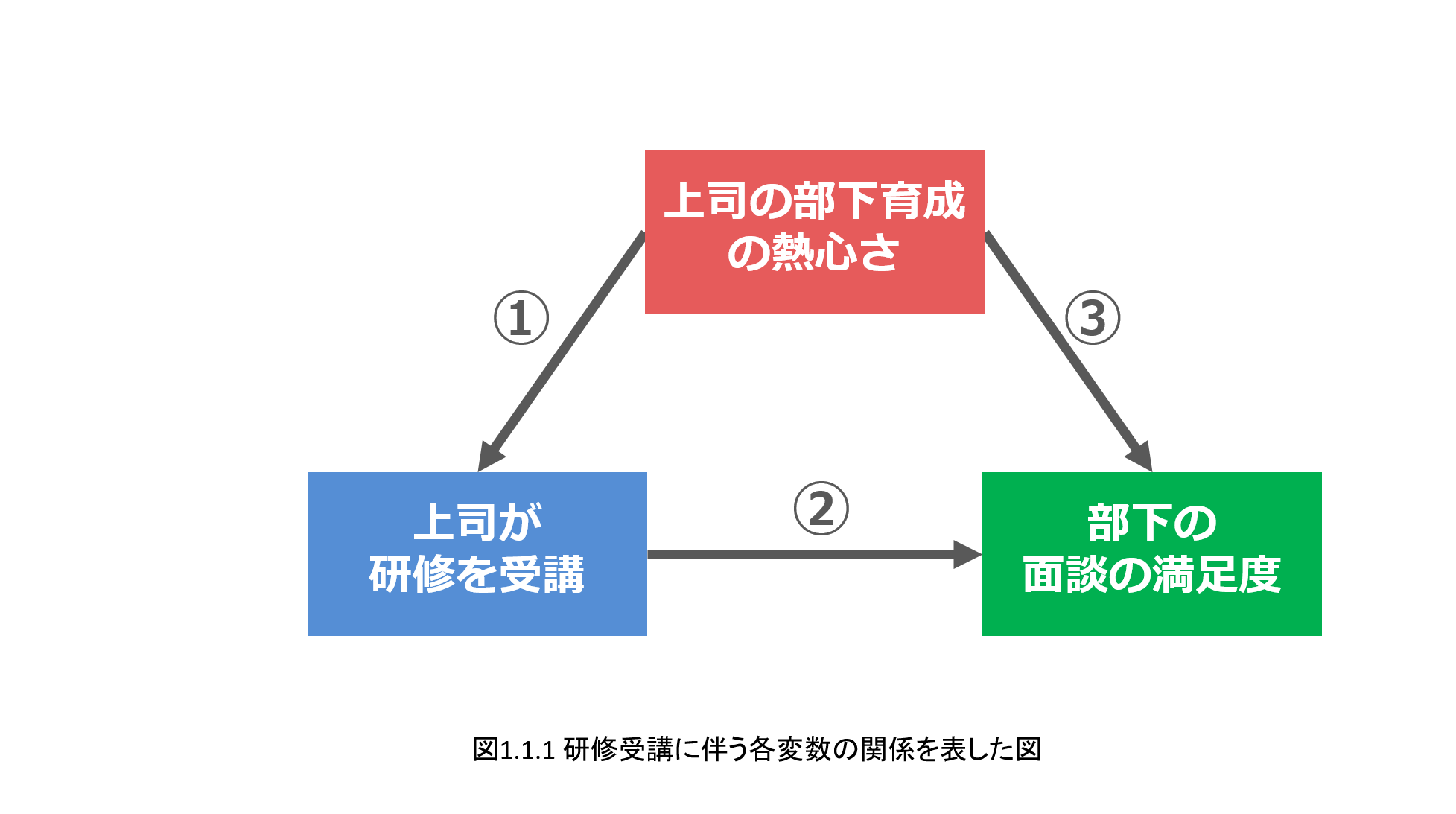
それでは、人事部長であるあなたが疑問に感じた、今回の会話内容を絵にしてみましょう(図1.1.1)。
図1.1.1を見ると、
・矢印①:【上司の部下育成の熱心さ】が高いと、上司が【「上司向け:部下とのキャリア面談のポイント研修」を受講】する確率は高くなる
・矢印②:【上司が研修を受講する】と、【部下のキャリア面談への満足度】が高くなる
という関係性があります。この矢印②が今回検証している研修の実施効果を示します。
矢印①、②の2本だけであれば、Aさんの報告は正しいのですが、人事部長のあなたが懸念を抱く通り、
・矢印③:【上司の部下育成の熱心さ】が高いと、【部下のキャリア面談への満足度】が高くなる
という矢印(関係性)も十分に想像できそうです。
よって図1.1.1においては、矢印③の存在も考慮しながら、矢印②による効果を推定しないと、研修実施による効果を正確に推定することはできません。
このように他の変数(要因)からの因果の効果(矢印の影響)も考慮しながら、求めたい直接的な因果の効果を推定する手法が因果推論です。
※なお、現実世界の職場においては、【部下のキャリア面談の満足度】は図1.1.1のような単純な3変数では表現できないと思います。この図1.1.1は、現実世界を単純にモデル化したものです。そのため、図1.1.1に描かれていない様々な要因は、この3つの変数にそれぞれ独自に影響する(すなわち、各変数にノイズとして加わる)という想定となります。
2. 因果推論をしたいデータ
今回の例に挙げた人事研修のデータを確認してみましょう。
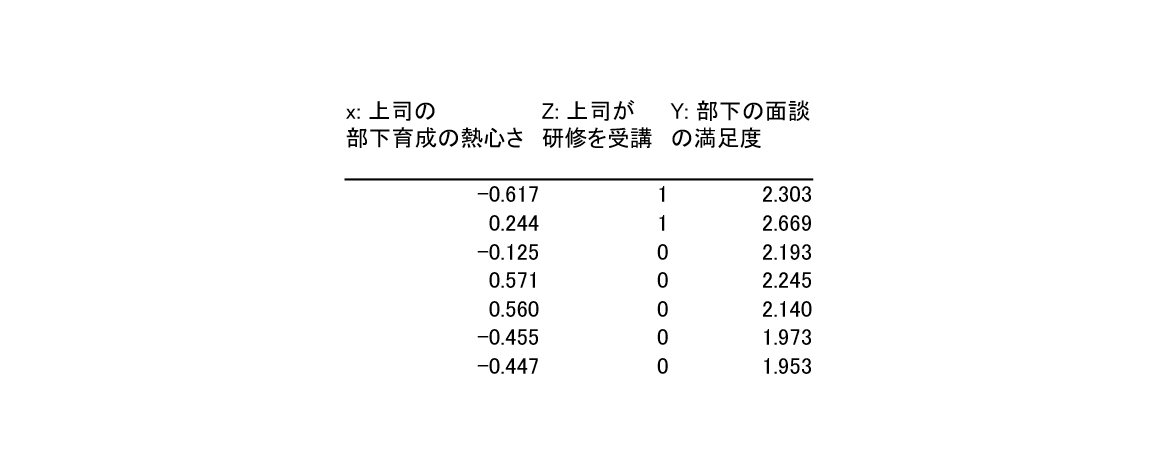
こんな感じのデータが続いています。
変数Zが研修の受講を示し、1が受講、0が未受講を示します。
この変数Zが1の場合、どれだけ、部下社員の面談の満足度は向上しているのでしょうか?
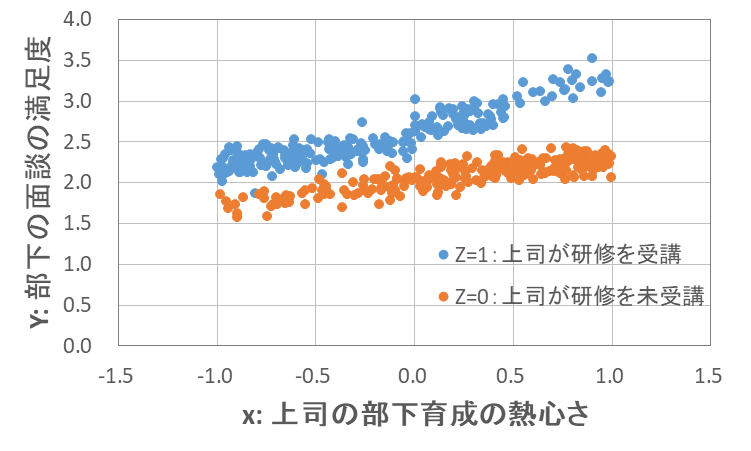
続いて、データをグラフで確認してます。
グラフより、
- 研修を受講している方が(Z=0よりZ=1の方が)、Y: 部下の面談の満足度が高いことが分かります
- 青点もオレンジ点もデータが右上がりの傾向があり、x: 上司の部下育成の熱心さが高いほど、Y: 部下の面談の満足度も高くなることが分かります。
「では、このデータから、研修Zの効果を求めてください。」
これが、企業で働くデータサイエンティストに与えられる課題(の一例)になります。
3. 因果推論の方法
それでは上記のデータを因果推論します。
ただし、本記事で因果推論の内容をすべて解説することは困難です。
つくりながら学ぶ! Pythonによる因果分析 ~因果推論・因果探索の実践入門では、第1章から第3章で、因果推論に必要な事前知識を解説しています。
**「第1章 相関と因果の違いを理解しよう」**では、人事研修とテレビCMを例に、施策を受けた集団と受けていない集団で単純に平均値の差を計算するだけでは、処置の効果は求められない点を解説します。
また平均値の差による推定が上手くいかない原因である疑似相関の概念を解説し、疑似相関が生まれる3つのパターンを解説します。
そして第1章の最後に、Google Colaboratory上で、疑似相関が生まれる3パターンを実際にプログラム実装して確認します。
**「第2章 因果効果の種類を把握しよう」**では、反実仮想、潜在的結果変数、そして種々の因果効果(ATEやATTなど)を紹介します。
そして、介入操作であるdoオペレータの紹介と、間接的な因果効果で疑似相関が生まれていると因果推論が困難であるが、介入操作で因果の矢印を消せることを解説します。
最後にこの介入操作を、doオペレータを使用せずに数式で記述する調整化公式について説明します。
**「第3章 グラフ表現とバックドア基準を理解しよう」**では、構造方程式モデル、因果ダイアグラム、そして有向非循環グラフDAGを導入します。
続いてDAGにおいて因果推論を実施するために、考慮すべき変数と無視すべき変数を整理しバックドアパスを閉じるd分離を解説します。
第1章から第3章で順番に因果推論に必要な知識を解説し、第4章から、具体的に因果推論の分析プログラムを実装・解説します。
**「第4章 因果推論を実装しよう」**では、基本的な因果推論手法である回帰分析、傾向スコアを用いたIPTW法、そして回帰分析とIPTW法を組み合わせたDR法について解説、実装を行います。
ただし、本記事で紹介しているさきほどの人事研修のデータはこの第4章の基本的な因果推論の手法では正確に効果が推定できない問題になっています。
具体的には、各変数(要因)が線形ではなく非線形に効いており、研修Zの効果が、x: 上司の部下育成の熱心さによって変化する、という問題に設定しています。
具体的には、
Y = Z×t(x) + 0.3x + 2.0 + 0.1×noize
で疑似データを作成しています。
まず、0.3xの項が存在するので、x: 上司の部下育成の熱心さ、が高いほど、Y: 部下の面談の満足度が高くなります
Z×t(x)の項があるので、研修を受講(Z=1)の上司は、t(x)の効果が追加されます(これが研修受講による効果です)。
このt(x)は今回、
・上司の部下育成の熱心さxが、0より小さいと効果が低く、満足度Yは0.5だけ上昇
・xが0以上で0.5より小さいと、満足度Yは0.7上昇
・xが0.5以上だと満足度Yは1.0上昇
とします。
すなわち研修効果が変数x: 上司の部下育成の熱心さ、によって変化するという、Zとxが絡む交互作用&非線形状態とします。
部下育成に熱心な上司ほど、同じ研修を受講してもその効果が大きいという状況は、現実問題としても妥当なシチュエーションかと思います。
最後に、そもそも研修を受講するかどうかのZですが、これは
Z_prob=sigmoid(5.0x-5.0*noise)
という、シグモイド関数で各人の研修受講確率Z_probを求め、確率Z_probで各人が受講するかどうか決まるとしています。
x: 上司の部下育成の熱心さ、が高いほど**「上司向け:部下とのキャリア面談のポイント研修」**を受講する確率が高くなる状況です。
以上が、疑似データの生成ルールです。
ですが、実際にデータとして取得できているのは、先に示した3つの変数の値、
x: 上司の部下育成の熱心さ
Y: 部下の面談の満足度
Z: 上司が研修を受講したかどうか
だけです。
今回は非線形な現象の因果推論を行いたいので、非線形な回帰モデルを構築する必要があります。
ここで機械学習が出てきます。
機械学習を使用した因果推論の手法としては、Meta-Learners(T-Learner、S-Learner、X-Learner)や、Doubly Robust Learningが一般的であり、本書ではこれらの手法を解説・実装しています。
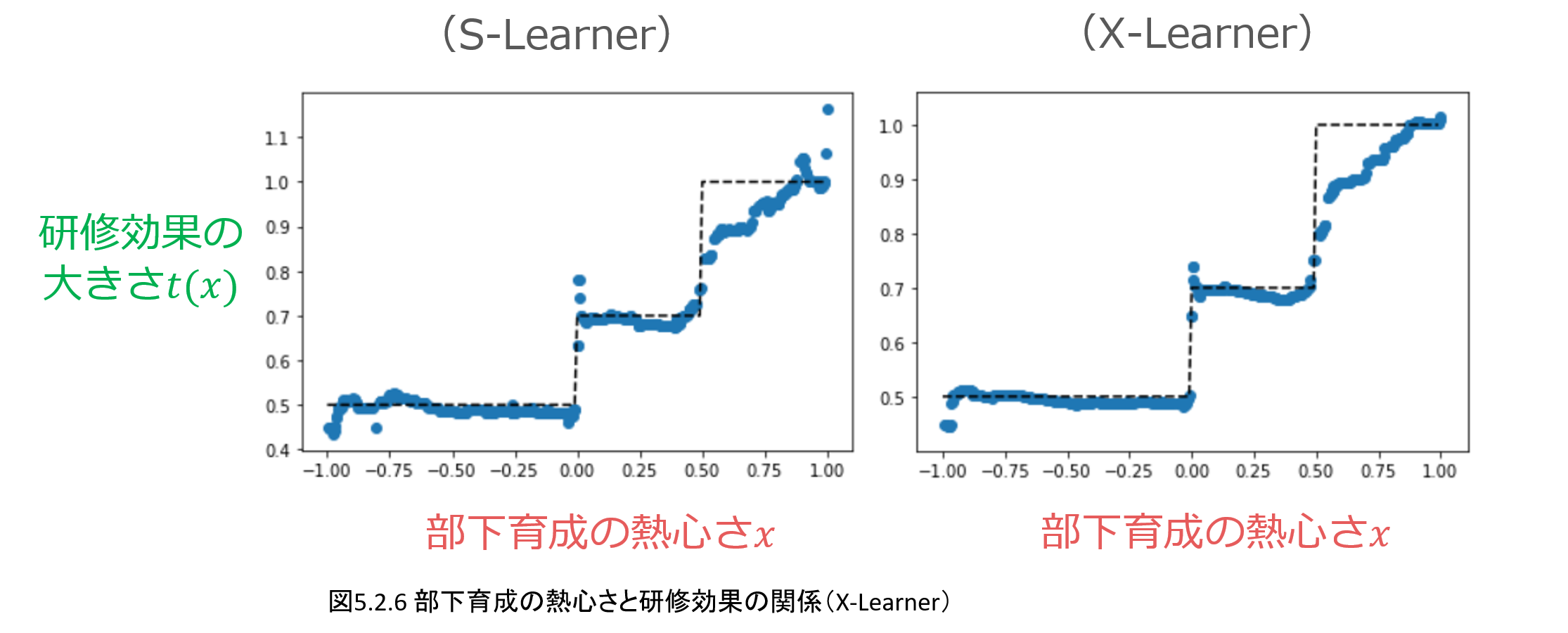
その具体的な手続きは本記事では解説しきれないのですが、S-Learner、X-Learnerを使用して研修効果を求めると以下のような結果になります。
S-LearnerよりはX-Learnerの方が正確に求まります。
どちらの手法も、x: 上司の部下育成の熱心さ、によって段階的に研修効果が変化している点がきちんと求まっています。
この因果推論の結果が、
「以下のデータから、研修Zの効果を求めてください。」
というビジネス課題に対する、解です。
この因果推論分析ができる能力を身につけることが、企業で働くデータサイエンティストとしては重要です。
本書籍、つくりながら学ぶ! Pythonによる因果分析 ~因果推論・因果探索の実践入門、の第1章から第5章までが「第1部 因果推論」です。
ここまでの因果推論の手法について、一歩ずつ解説します。
4. 因果探索の手法
第6章から第8章は「第2部 因果探索」です。
因果推論では因果の関係性、因果の向きを既知としていました。
因果探索ではこの因果関係が不明で、その関係性を推定します。
例えば、
●生活習慣と疾病の大規模アンケート
●企業における、働きやすさ、仕事のやりがい、組織や上司への満足度など、働き方改革に伴う社員の意識調査
など、
多くの項目をアンケート調査などで収集した後に、調査項目間に存在する因果関係を求める手法です。
**「第6章 LiNGAMの実装」**では線形で非巡回、そして非ガウスなノイズによる構造方程式モデルを前提としたLiNGAMによる因果探索について、解説、実装します。
独立成分分析と密接に関係していること、構造方程式モデルを求めることがLiNGAMのポイントであり、その点を解説しながら、実際に実装しながら、アルゴリズムの流れを解説します。
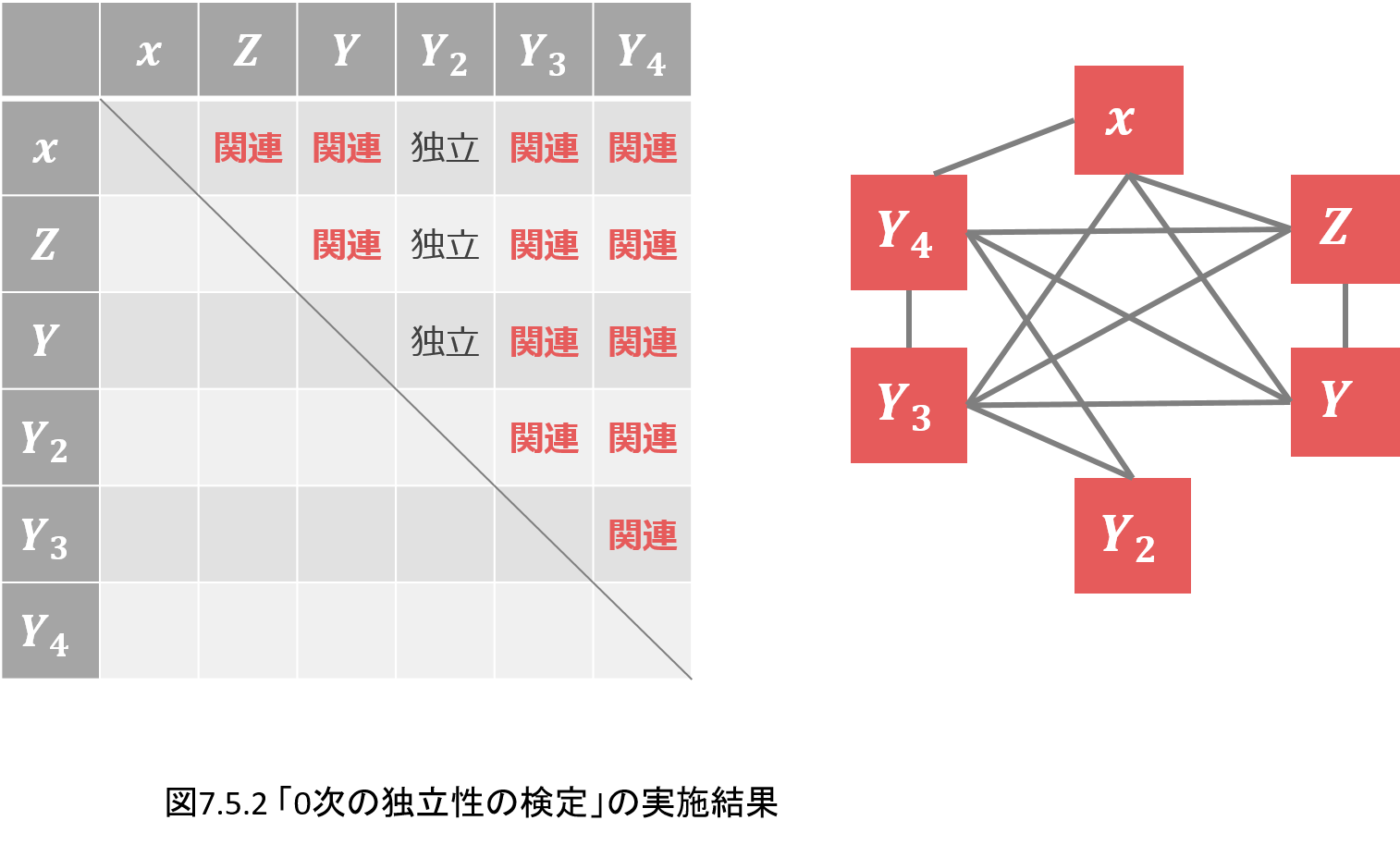
**「第7章 ベイジアンネットワークの実装」**ではベイジアンネットワークの解説として、はじめにスケルトン、PDAG、条件付き確率表CPTを紹介します。
そして、ベイジアンネットワークに対する観測データの当てはまりの良さを示すベイジアンスコアとしてBICを取り挙げ、その計算を解説、実装します。
続いて2つの変数の独立性を検定する手法について解説、実装し、3種類のネットワーク推定手法を紹介します。
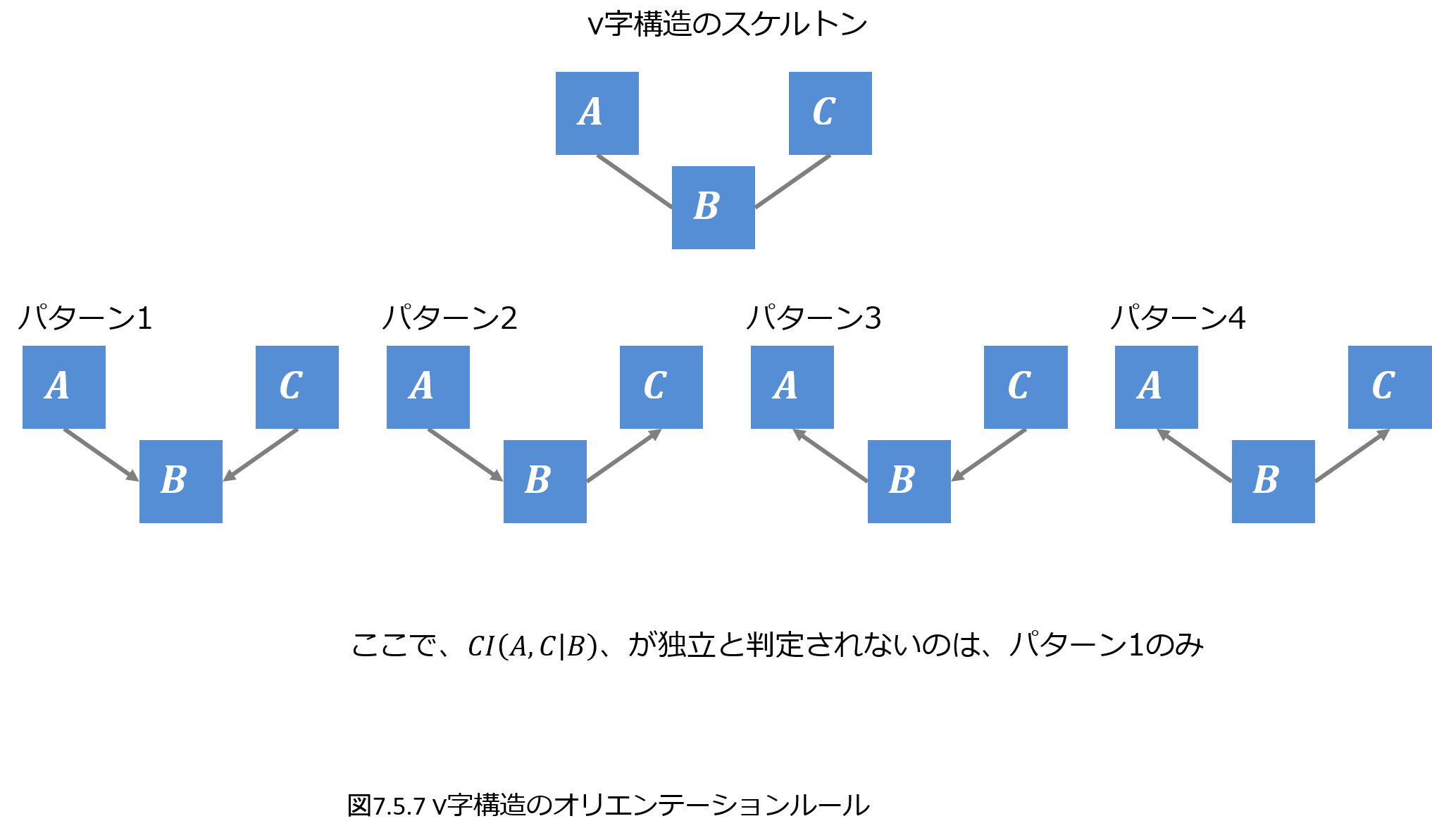
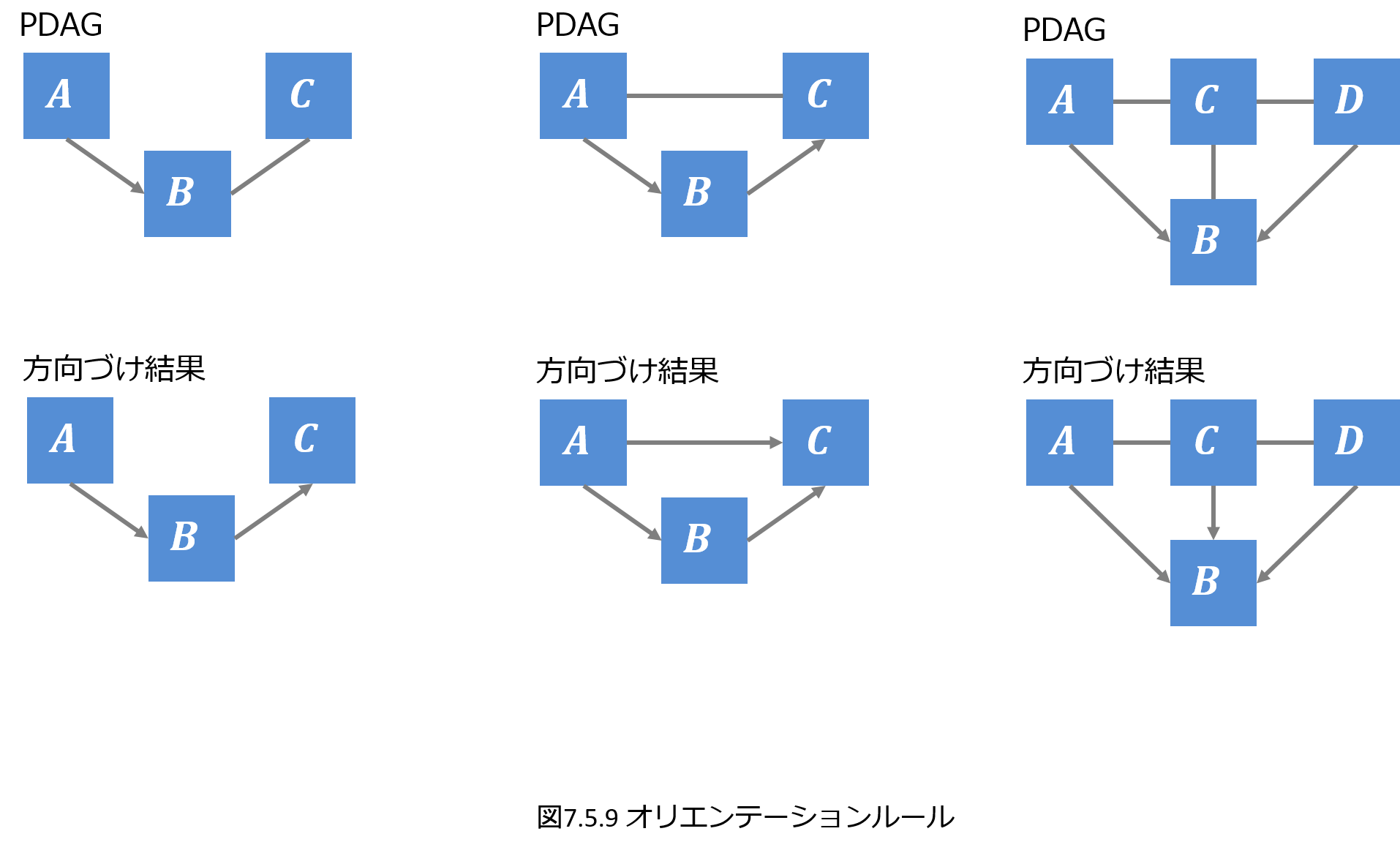
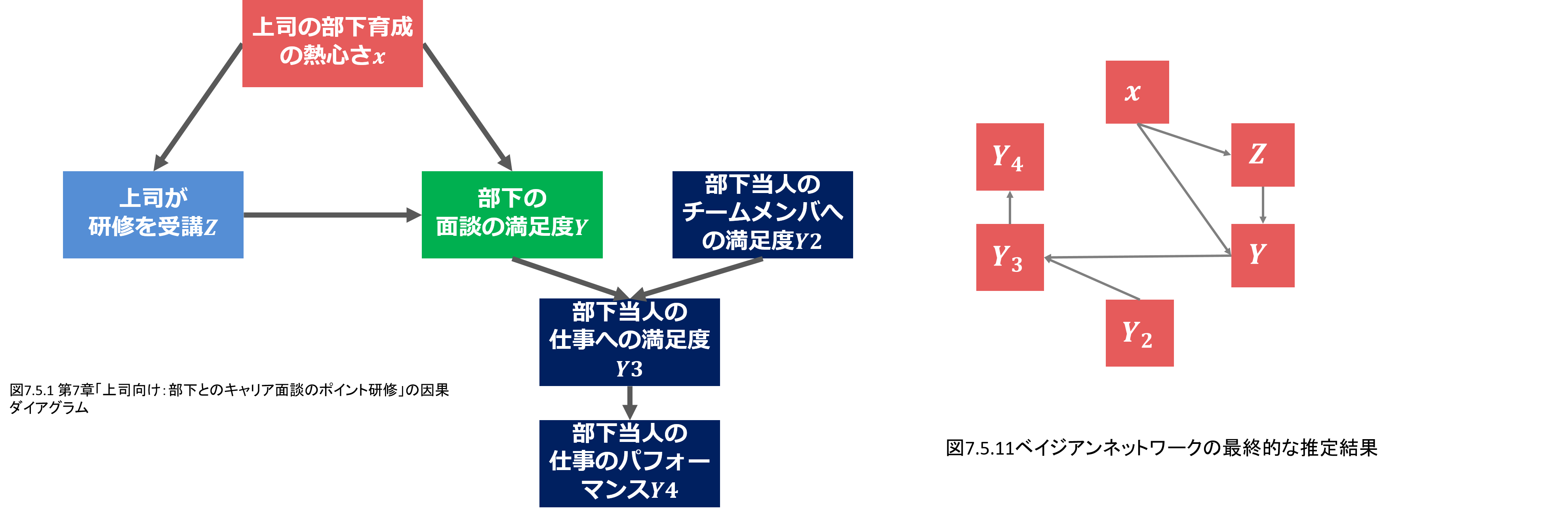
最後に7.5節では条件付き独立検定による構造学習の手法としてPCアルゴリズムを紹介し、「上司向け:部下とのキャリア面談のポイント研修」を少し複雑にしたデータで、ベイジアンネットワークを推定、推定したネットワークから未観測の変数の値の推定を実施します。
因果分析・因果探索においては機械学習やディープラーニングだけでなく、ベイジアンネットワークも重要ですが、ベイジアンネットワークについて、簡潔に書かれた書籍は少ないように感じます。
本書がベイジアンネットワークの入門として、ベイジアンネットワークの世界観を学べる良い入門書になるように心がけました。
本章の内容は、以下のようなイメージです。
5. ディープラーニング × 因果探索
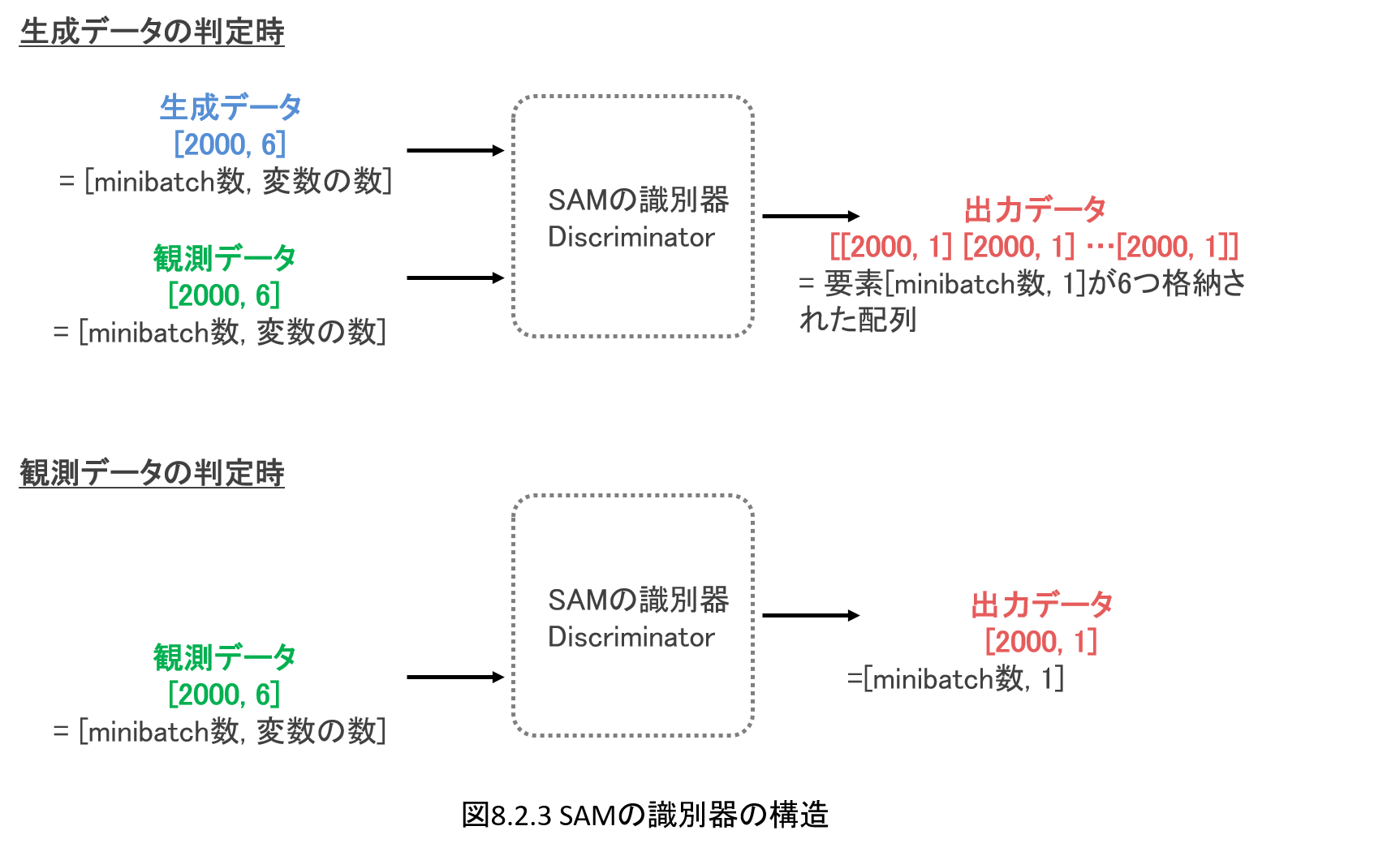
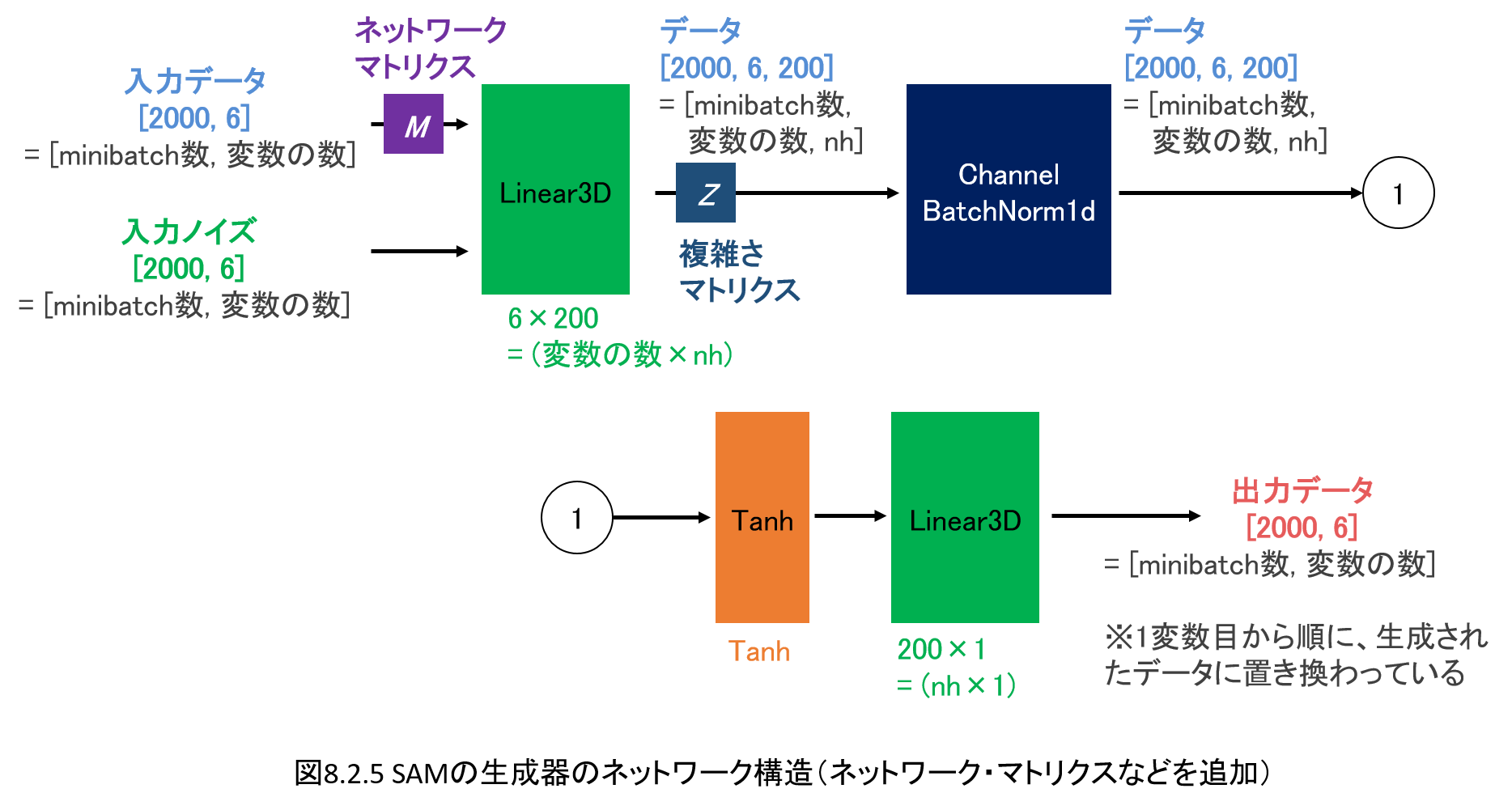
本書の最後、**「第8章 ディープラーニングを用いた因果探索」**では、ディープラーニングのGAN(敵対的生成ネットワーク)の技術をベースとした因果探索をとりあげ、その概要、ネットワーク構造、そして実際の因果探索の実施について、解説、実装を行います。
2020年現在、ディープラーニングを様々な領域で利用する研究が増えており、因果探索の分野でもディープラーニングを利用した研究が進んでいます。
例えば、
・グラフニューラルネットワークを用いた因果探索
・深層強化学習を用いた因果探索
・GAN(Generative Adversarial Networks)を用いた因果探索
などが発表されています。
ディープラーニングを用いた因果探索手法は、まだまだ研究が始まったばかりの分野であり、今後より洗練された手法が発表されると考えています。
そのため本書にてディープラーニングを用いた因果探索を掲載するか迷いましたが、読者の皆様に、今後発展が期待される分野を感じていただきたいと考えて、本書の最後で解説、実装することとしました。
本書ではディープラーニングを用いた因果探索手法の中でも、GANを用いた因果探索手法である**SAM(Structural Agnostic Model)**について、解説、実装を行います。
以下のようなイメージで、図解でSAMの概念やネットワーク構成を解説したのちに、実際にコードを実装し、因果探索を実施します。
本書の内容はすべてGoogle Colaboratoryで実施できるようにしており、SAMによる因果探索もGoogle ColaboratoryでGPUを使用して実施します。
本書の8.5節でGoogle ColaboratoryでGPUを使用する方法も解説します。
さいごに
以上、Pythonによる因果推論と因果探索(初心者向け)書籍の紹介でした。
「つくりながら学ぶ! Pythonによる因果分析 ~因果推論・因果探索の実践入門」
●2020年6月30日発売
●著者:小川雄太郎(自己紹介、[Twitter] (https://twitter.com/ISID_AI_team))@(株)電通国際情報サービス(ISID)
●出版社: マイナビ出版
以上、ご一読いただき、ありがとうございました。
【文責】電通国際情報サービス(ISID) AIトランスフォーメーションセンター 開発グループ
小川 雄太郎
【免責】本記事の内容そのものは著者の意見/発信であり、著者が属する企業等の公式見解ではございません
【備考】電通国際情報サービス(ISID)のAI部開発チームではメンバを絶賛募集中です。興味がある方は是非こちらから