More than 3 years have passed since last update.

ワルラス法則とミクロ主体予算制約式を用いたインフレ目標達成への検討

Last updated at 2021-06-09Posted at 2021-06-09

はじめに

ワルラス法則とミクロ主体予算制約式¹を用いて、インフレ目標達成への検討を行なった。

レポジトリーはこちらです。

ワルラス法則とミクロ主体予算制約式¹


P1(t)*(y(t) - c(t)) + P2(t)*(b(t-1) - b(t)) +P2(t)*(bc(t-1) - bc(t)) + W(t)*(ls(t) - Id(t)) = MD(t) - MS(t)

P1:財価格 y:財供給 c:財消費 P2:債券価格 b:家計保有債券 bc:政府保有債券 W:賃金 ls:労働供給 ld:労働需給マネー需要:MD MS:マネー供給

上式の意味は以下の通りである。

マネーの超過供給量は、通貨発酵益を経由して、財の超過需要を生み出している。¹

本論では、以下の政策を実施する。

政府政策
・インフレ目標2%
・GDP600兆円を目指す

日銀政策
・フォワードガイダンス
・量的緩和(毎年80兆円の国債買い入れ、内民間と統合政府それぞれの保有残高増しは25兆円とする)

また、上式の制約として、

一般の政府と中央銀行の統合政府を考える。ただし、簡単のために一般の政府は重要な役割を果たさず、統合政府は中央銀行とする。¹

次回以降、
・イールドカーブコントロール
・為替とGDPの関係(消費、投資、政府支出、輸出入)

の検討とそれらを加味したモデルの検討を行いたい。

フィリップス曲線

インフレ率と失業率には強い逆相関(フィリップス曲線)があることが知られている。そこで、フィリップス曲線を用いて、インフレ率から失業率を導出する。

インポート

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from google.colab import drive
import time

from sklearn.linear_model import LinearRegression

drive.mount('/content/drive/')
nov_dir = 'Colab Notebooks/dataset/phillips_curve/'
work_dir = 'Colab Notebooks/workspace/export/'
uer_path = '/content/drive/My Drive/' + nov_dir + 'UnemploymentRate.csv'
cpi_path = '/content/drive/My Drive/' + nov_dir + 'corecoreCPI.csv'
save_path = '/content/drive/My Drive/' + work_dir


df_uer = pd.read_csv(uer_path, index_col='DATE', parse_dates=True)
df_cpi = pd.read_csv(cpi_path, index_col='DATE', parse_dates=True)
df_cpi = df_cpi[df_cpi.index != '2021-04-01']

print(df_uer.shape)
print(df_cpi.shape)
print(df_uer.head())
print(df_cpi.head())

Mounted at /content/drive/
(603, 1)
(603, 1)
            UnemploymentRate
DATE                        
1971-01-01               1.1
1971-02-01               1.2
1971-03-01               1.2
1971-04-01               1.2
1971-05-01               1.2
            corecoreCPI
DATE                   
1971-01-01          6.5
1971-02-01          6.2
1971-03-01          6.2
1971-04-01          6.8
1971-05-01          7.3

描写

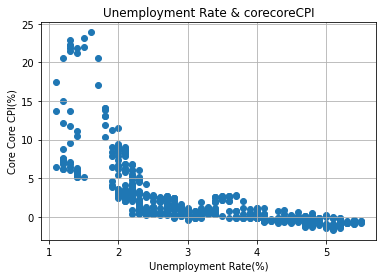
plt.scatter(df_uer['UnemploymentRate'], df_cpi['corecoreCPI'])

plt.title('Unemployment Rate & corecoreCPI')
plt.xlabel('Unemployment Rate(%)')
plt.ylabel('Core Core CPI(%)')
plt.grid()

plt.savefig(save_path+'PhillipsCurvePlot.png')

plt.show()

教育

model = LinearRegression()

X = df_uer[['UnemploymentRate']].values
Y = df_cpi['corecoreCPI'].values

model.fit(X, Y)

a=model.intercept_
b=model.coef_
r2=model.score(X,Y)

p_y=a/X+b

描写と保存

plt.scatter(X, Y)
plt.plot(X, p_y, color='red', label="Phillips Curve")
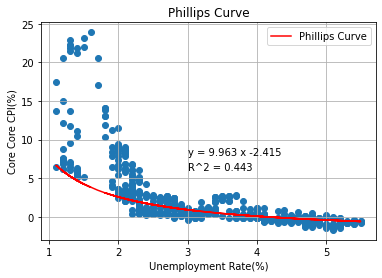
plt.title('Phillips Curve')

plt.xlabel('Unemployment Rate(%)')
plt.ylabel('Core Core CPI(%)')
plt.grid()

plt.text(3, 8, 'y = %s x %s' % (round(a,3),round(b[0],3)))
plt.text(3, 6, 'R^2 = %s' % round(r2,3))

plt.legend()

plt.savefig(save_path+'PhillipsCurve.png')
plt.show()

フィリップス曲線の結果より、
(インフレ率,失業率) = (2,2.567)
となることがわかった。

乗数効果

内閣府の調査によれば、以下の乗数があることがわかった。(ともに2015年)²

名称	乗数
公共投資	1.14
減税	0.30

以上より以下のことがわかる。

公共投資の乗数効果は、短期目的には減税のそれよりも大きい。²

また、乗数効果の式は以下の式である。

\Delta Y = \alpha \Delta G \\

\Delta Y:国民所得,\alpha:乗数,G:政府支出

ここで、政府支出は一般会計の国費と限定する。

令和3年の12ヶ月会計

名称	額面(兆円)
国費	23.8

信用乗数(貨幣乗数)の推定

一般にマネタリーベースとマネーストックとの関係がある。

\Delta M = m \Delta H \\
\Delta M: マネタリーベース,m: 信用乗数,\Delta H: マネーストック

しかし、景気循環にタイムラグがあり、定数が一定でないことが知られている。
そこで、関係性を調査し、可能であれば、推定を行いたい。

マネタリーベースのデータ加工

df = pd.read_excel(mbase_path, sheet_name=excel_sheet_name)
df = df.drop(range(6))
df = pd.concat([df['Unnamed: 1'], df['Unnamed: 7']], axis=1)
df = df.rename(columns={'Unnamed: 1': 'DATE', 'Unnamed: 7': 'MONETTALYBASE'})
df['DATE'] = pd.to_datetime(df['DATE'], format='%Y%m%d')
df = df.reset_index(drop=True)
drop_index = df.index[(df.index >= 612)]
df = df.drop(drop_index)
drop_index = df.index[(df.index <= 551)]
df = df.drop(drop_index)
df = df.set_index('DATE')
df.index = df.index.strftime('%Y/%m')
df.tail()

マネーストックのデータ加工

df2 = pd.read_csv(mstock_path,encoding='cp932')
df2 = df2[df2.index != 0]
df2 = df2.rename(columns={'データコード': 'DATE','MD02\'MAM1NAM2M2MO': 'MONEYSTOCK'})
df2 = df2.drop(['MD02\'MAM1NAM3CCMO','MD02\'MAM1NAM3DMMO'], axis=1)
df2 = df2.reset_index(drop=True)
drop_index = df2.index[(df2.index >= 60)]
df2 = df2.drop(drop_index)
df2 = df2.set_index('DATE')
df2.tail()

信用乗数

df3 = pd.concat([df['MONETTALYBASE'], df2['MONEYSTOCK']], axis=1)
df3['MONEYSTOCK'] = df3['MONEYSTOCK'].astype(int)
df3['MoneyMultiplier'] = df3['MONEYSTOCK']/df3['MONETTALYBASE']
df3 = df3.drop(['MONEYSTOCK','MONETTALYBASE'], axis=1)
serial_num = pd.RangeIndex(start=1, stop=len(df.index) + 1, step=1)
df3['No'] = serial_num
df3.tail()

描画

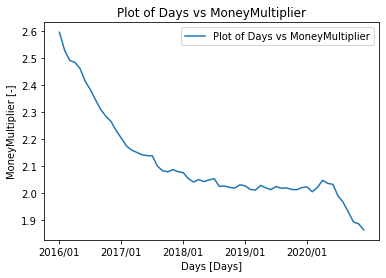
plt.plot(df3.index,df3['MoneyMultiplier'], label="Plot of Days vs MoneyMultiplier")
plt.title('Plot of Days vs MoneyMultiplier')
plt.ylabel('MoneyMultiplier [-]')
plt.xlabel('Days [Days]')
plt.xticks(['2016/01','2017/01', '2018/01','2019/01', '2020/01'])
plt.legend()
plt.show()

教育

model = LinearRegression()

X = df3[['No']].values
Y = df3['MoneyMultiplier'].values

model.fit(X, Y)
a=model.coef_[0]
b=model.intercept_
r2=model.score(X,Y)
print('coefficient = ', model.coef_[0])
print('intercept = ', model.intercept_)

coefficient =  -0.008187783320053916
intercept =  2.3618821612964167

描画と保存

fig = plt.figure()

plt.plot(df3.index,df3['MoneyMultiplier'], color = 'blue', label="Plot of Days vs MoneyMultiplier")
plt.plot(X, model.predict(X), color = 'red', label="Estimated Money multiplier")

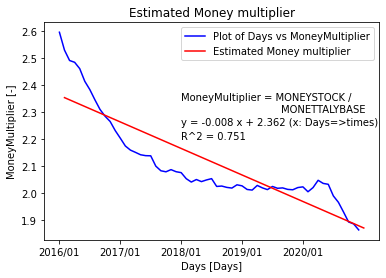
plt.title('Estimated Money multiplier')
plt.ylabel('MoneyMultiplier [-]')
plt.xlabel('Days [Days]')
plt.xticks(['2016/01','2017/01', '2018/01','2019/01', '2020/01'])

plt.text(24, 2.3, 'MoneyMultiplier = MONEYSTOCK / \n                                MONETTALYBASE')
plt.text(24, 2.25, 'y = %s x + %s (x: Days=>times)' % (round(a,3),round(b,3)))
plt.text(24, 2.2, 'R^2 = %s' % round(r2,3))
plt.legend()
fig.savefig(save_path)
plt.show()

以上より、信用乗数を2.0と推定する。

マネタリーベースの平均変化率

マネタリーベースの定義は以下の通りである。

マネタリーベース＝「日本銀行券発行高」＋「貨幣流通高」＋「日銀当座預金」³

EXCELデータの読み込み加工

df = pd.read_excel(mbase_path, sheet_name=excel_sheet_name)
df = df.drop(range(6))
df = pd.concat([df['Unnamed: 1'], df['Unnamed: 7']], axis=1)
df = df.rename(columns={'Unnamed: 1': 'DATE', 'Unnamed: 7': 'MONETTALYBASE'})
df['DATE'] = pd.to_datetime(df['DATE'], format='%Y%m%d')
df = df.reset_index(drop=True)
drop_index = df.index[(df.index >= 612)]
df = df.drop(drop_index)
df = df.set_index('DATE')
df.head()

年の増加率

df2 = df[(df.index.month == 1)]
df2.index = df2.index.year
df2 = df2.rename(columns={'MONETTALYBASE':'JAN'})

df3 = df[(df.index.month == 12)]
df3.index = df3.index.year
df3 = df3.rename(columns={'MONETTALYBASE':'DEC'})

dfy = pd.concat([df2['JAN'], df3['DEC']], axis=1)
dfy['MONETTALYBASE'] = dfy['DEC'] - dfy['JAN']
dfy = dfy.drop(['DEC', 'JAN'], axis=1)
dfy.to_csv(save_path, sep=",")
dfy.tail()

描画

fig = plt.figure()

plt.plot(dfy.index,dfy['MONETTALYBASE'], label="Plot of Years vs Average rate of change")

plt.title('Plot of Days vs MoneyMultiplier')
plt.ylabel('Average rate of change [-]')
plt.xlabel('Years [Years]')
plt.legend()

fig.savefig(save_path4)
plt.show()

期待GDPとマネタリーベースの算出

GDP=23.8*1.14
print('GDP  =' + str(round(GDP,2)))
now_GDP=df2['REAL'][0]
print(now_GDP)
for_GDP=now_GDP+GDP
print('for_GDP  =' + str(for_GDP))
all_wage = df2['REAL'][2] * df2['REAL'][3]*0.000000000001
print('all_wage  =' + str(all_wage))
for_mometqary_base=(50+all_wage+GDP)/2
print('for_mometqary_base  ='+str(round(for_mometqary_base,2)))

now_GDP  =27.13
535.7
for_GDP  =562.832
all_wage  =9.3075
for_mometqary_base  =43.22

以上より、
完全雇用(インフレ率2%)を達成した時の
予想名目GDPは、562兆円
予想マネタリーベースは43兆円
と妥当性が高く、可能性は高い。
GDP600兆円は達成できないと思われる。

岩田喜久男編、まずデフレを止めよ、日本経済新聞社、2003年 ↩ ↩² ↩³ ↩⁴
社会資本整備等の現状 ↩ ↩²
「マネタリーベース」とは何ですか？ ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up