はじめに
近年、人工知能ブームにより、人工知能を使ったトレーディング手法が盛んである。そこで、今回は深層強化学習を用いたシステムトレーディングを実施した。
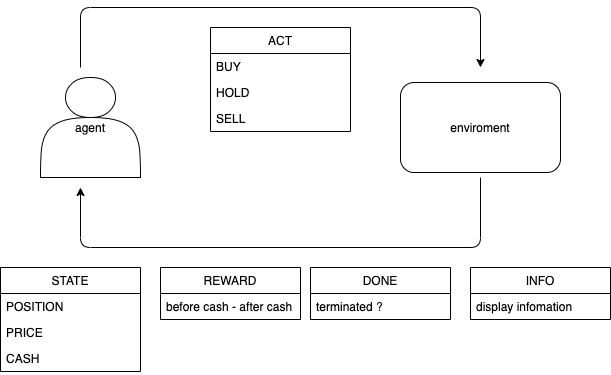
まず、基本的な深層強化学習を用いたトレーディングモデルである。agentの行動として、 BUY、HOLD、SELLの三つの内一つを選択する。環境の戻り値として、状態(今現在保有しているポジションの価格、市場価格、手持ちのキャッシュ)、報酬(手持ちのキャッシュの変化値(含む益も含む))、終了(取引の終了か否か)、情報(ターミナルにディスプレイする情報)を返す。
使用データについて
トレンド傾向の掴みやすさから、yahoo financeからGSPCの日足を使用した。
訓練データの期間:2015/1/1 - 2017/6/30
テストデータの期間:2017/7/1 - 2021/1/1
以下ソースコード
TD学習
TD学習(時間的差分学習: Temporal Difference Learning)とは、代表的な価値ベース手法一つである。逐次的にデータ更新ができるのが特徴。
以下、TD学習での状態価値の更新式。
\Delta V(s) = r + \gamma V(s_{t+1}) - V(s_t) \\
A2C1
A2C(Advantage Actor-Critic)とは、A3C(Asynchronous Advantage Actor-Critic)から、非同期の部分を抜いたものであり、A3Cと比べてGPUの負荷が低い。
Q学習で使用したQ値は、状態価値関数V(s)とアドバンテージ値A(s, a)の2つに分解できる。このアドバンテージ関数とは、ある状態において、ある行動が他の行動に比較しどの程度優れているかを表す。価値関数とは、その状態に優位度を表す。
つまり、Actorはアドバンテージ値を通しQ値を学ぶ。これによりある行動の評価は、その行動がどれだけ良いかだけでなく、どれだけ良くなるかにも基づいて行われる。アドバンテージ関数の利点は、状態価値関数V(s)をベースラインとして使用することで、政策ネットワークの高い分散を減らし、モデルを安定させる。
A(s_t,a_t) = Q(s_t,a_t) - V(s_t) \\
A3C2
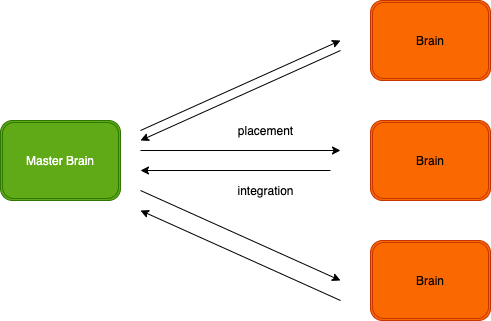
A3Cは並列分散処理を行なってる。処理速度が早い。個別のスレッドが学習した重みはmasterBrainに蓄積される。新しい、学習が始まる時に、各スレッドがmasterBrainから重みをコピーする。
マルチスレッド
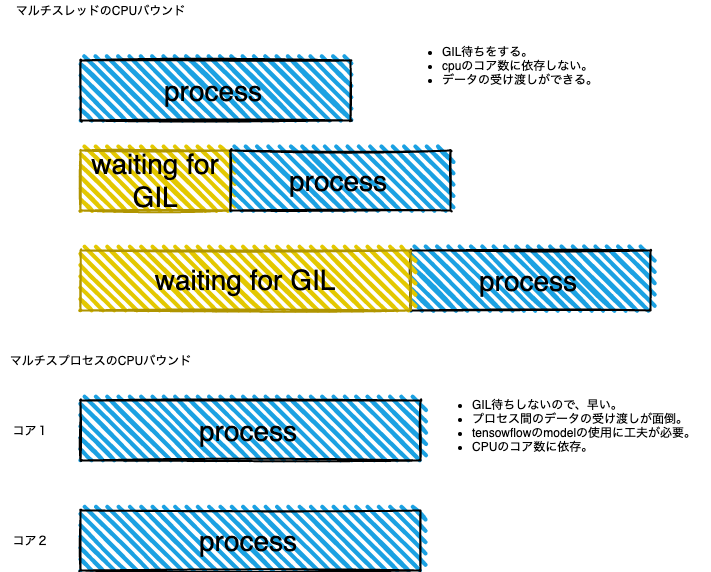
マルチスレッドの特徴は以下の通り
・平行処理
・GILロックを持っているスレッドのみ、実行可能、他のスレッドは待機する。
・cpuのコア数に依存しない。
マルチプロセスの特徴は以下の通り
・並列処理
・メモリーが共有されていないので、値の受け渡しが大変。
・tensowflowだと、modelが動かないことがある。
・cpuのコア一つにプロセスを割り当てする。
cpuバウンドとはcpu内で行なっている数値計算などの処理
ループ
class Task:
def __init__(self, name):
self.name = name
self.num = 0
self.sum = 0.0
def run(self):
while True:
sleep(1)
if self.num == 3:
break
print('roop_name = ' + self.name + ' :num = '+ str(self.num) + ' :sum = '+ str(self.sum))
self.num += 1
self.sum += random.random()
name = 'nomal-roop'
start = time.time()
for i in range(4):
w = Task('roop_point_'+str(i))
w.run()
end = time.time() - start
arr.append("name:" + name + " process_time:{0}".format(end) + "[s]")
roop_name = roop_point_0 :num = 0 :sum = 0.0
roop_name = roop_point_0 :num = 1 :sum = 0.642469181212962
roop_name = roop_point_0 :num = 2 :sum = 1.5964812171373977
roop_name = roop_point_1 :num = 0 :sum = 0.0
roop_name = roop_point_1 :num = 1 :sum = 0.8876820994429431
roop_name = roop_point_1 :num = 2 :sum = 1.627826300716026
roop_name = roop_point_2 :num = 0 :sum = 0.0
roop_name = roop_point_2 :num = 1 :sum = 0.03546302344611851
roop_name = roop_point_2 :num = 2 :sum = 1.0239282875765587
roop_name = roop_point_3 :num = 0 :sum = 0.0
roop_name = roop_point_3 :num = 1 :sum = 0.602393530385244
roop_name = roop_point_3 :num = 2 :sum = 1.555539488491399
マルチスレッド
class Task:
def __init__(self, name):
self.name = name
self.num = 0
self.sum = 0.0
def run(self):
while True:
sleep(1)
if self.num == 3:
break
print('roop_name = ' + self.name + ' :num = ' + str(self.num) + ' :sum = ' + str(self.sum))
self.num += 1
self.sum += random.random()
name = 'thread-pool'
start = time.time()
thread_num = 4
threads = []
for i in range(thread_num):
threads.append(Task(name=f'thread_{i}'))
datas = []
with ThreadPoolExecutor(max_workers = thread_num) as executor:
for task in threads:
job = lambda: task.run()
datas.append(executor.submit(job))
end = time.time() - start
arr.append("name:" + name + " process_time:{0}".format(end) + "[s]")
roop_name = thread_0 :num = 0 :sum = 0.0
roop_name = thread_1 :num = 0 :sum = 0.0
roop_name = thread_2 :num = 0 :sum = 0.0
roop_name = thread_3 :num = 0 :sum = 0.0
roop_name = thread_0 :num = 1 :sum = 0.7829927782861958
roop_name = thread_2 :num = 1 :sum = 0.7264674393557742
roop_name = thread_1 :num = 1 :sum = 0.4721450639806136
roop_name = thread_3 :num = 1 :sum = 0.2746835685320669
roop_name = thread_0 :num = 2 :sum = 0.8189509274906515
roop_name = thread_1 :num = 2 :sum = 0.7522106668563098
roop_name = thread_2 :num = 2 :sum = 1.3346477522815392
roop_name = thread_3 :num = 2 :sum = 0.33216049073474685
損失関数3
損失関数(更新式)は、損失関数(Actor)と損失関数(Critic)に分解できる。
L = L_v + L_π
損失関数(Actor)と損失関数(Critic)は以下の式に分解できる。アドバンテージ値A(s, a)は、一般的なTD学習での状態価値の更新式より、時系列を加味した形式になっている。Hはエントロピー。
L_v = (A(s_t,a_t))^2 \\
L_π = -log(π(a_t,s_t))A(s_t,a_t) - \beta H(π(s_t)) \\
A(s_t,a_t) \approx TD error = r + \gamma V(s_{t+1}) - V(s_t) \\
H(π(s_t)) = 1/2(log(2π \sigma ^2) + 1) \\
\beta:ハイパーパラメータ、\gamma:割引係数、\sigma:分散
売買ルール
1.空売りは認めない
2.ポジションを持っている場合、追加注文を出せない。
3.最後のステップでポジションを全て売却する。
4.ポジションは全買い、全売り
5.所持金は1000000ドル
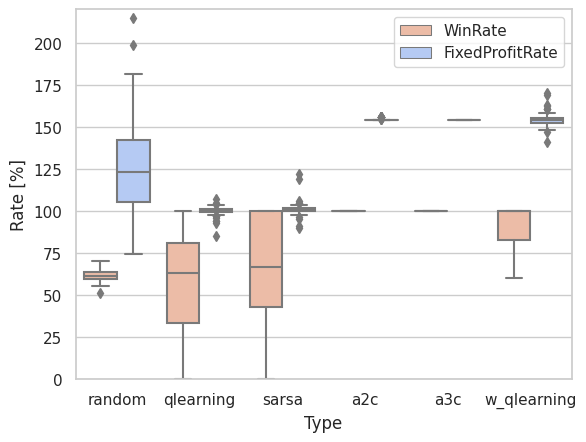
実装と結果
ソースコードはこちら
当然の事ながら、A2Cと同じパフォーマンスである。
ソースコードはこちら
-
V. Mnih, A. P. Badia, M. Mirza, A. Graves, T. Lillicrap, T. Harley, D. Silver, and K. Kavukcuoglu, “Asynchronous methods for deep rein- forcement learning,” in International conference on machine learning, (2016), pp. 1928–1937. ↩
-
V. Mnih, A. P. Badia, M. Mirza, A. Graves, T. P. Lillicrap, T. Harley, D. Silver, K. Kavukcuoglu, "Asynchronous Methods for Deep Reinforcement Learning",(2016), pp. 1602–1783. ↩
-
S. Kuutti, R. Bowden, H. Joshi, R.D Temple, and S. Fallah, "End-to-end Reinforcement Learning for Autonomous Longitudinal Control Using Advantage Actor Critic with Temporal Context", IEEE Intelligent Transportation Systems Conference (ITSC),(2019) ↩