突然だけど、persistent homologyをRで計算してみたのでまとめておく。
パッケージ
TDA
https://cran.r-project.org/web/packages/TDA/index.html
sample data
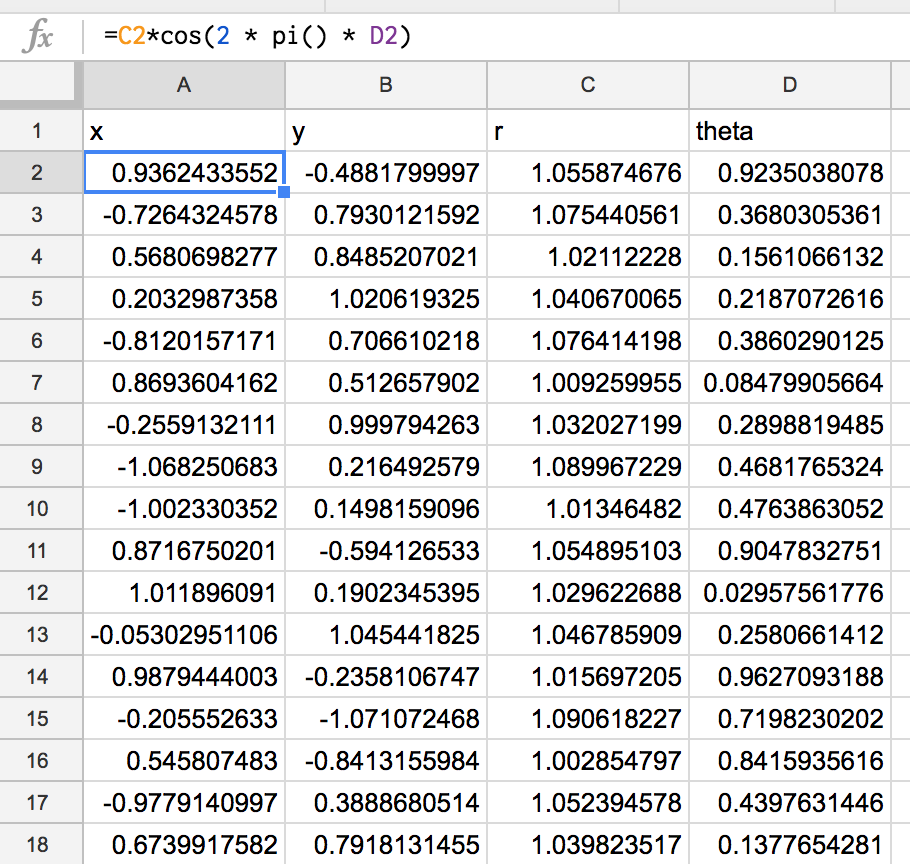
spreadsheetで適当にデータを生成。
今回は$S^1$と$T^2$
円周
x = r \cos(\theta) \\
y = r \sin(\theta)
この式と、
r = 1 + .1 * rand(), (theta) = 2 * pi() * rand()
をあわせて、spreadsheetで1000dataを生成
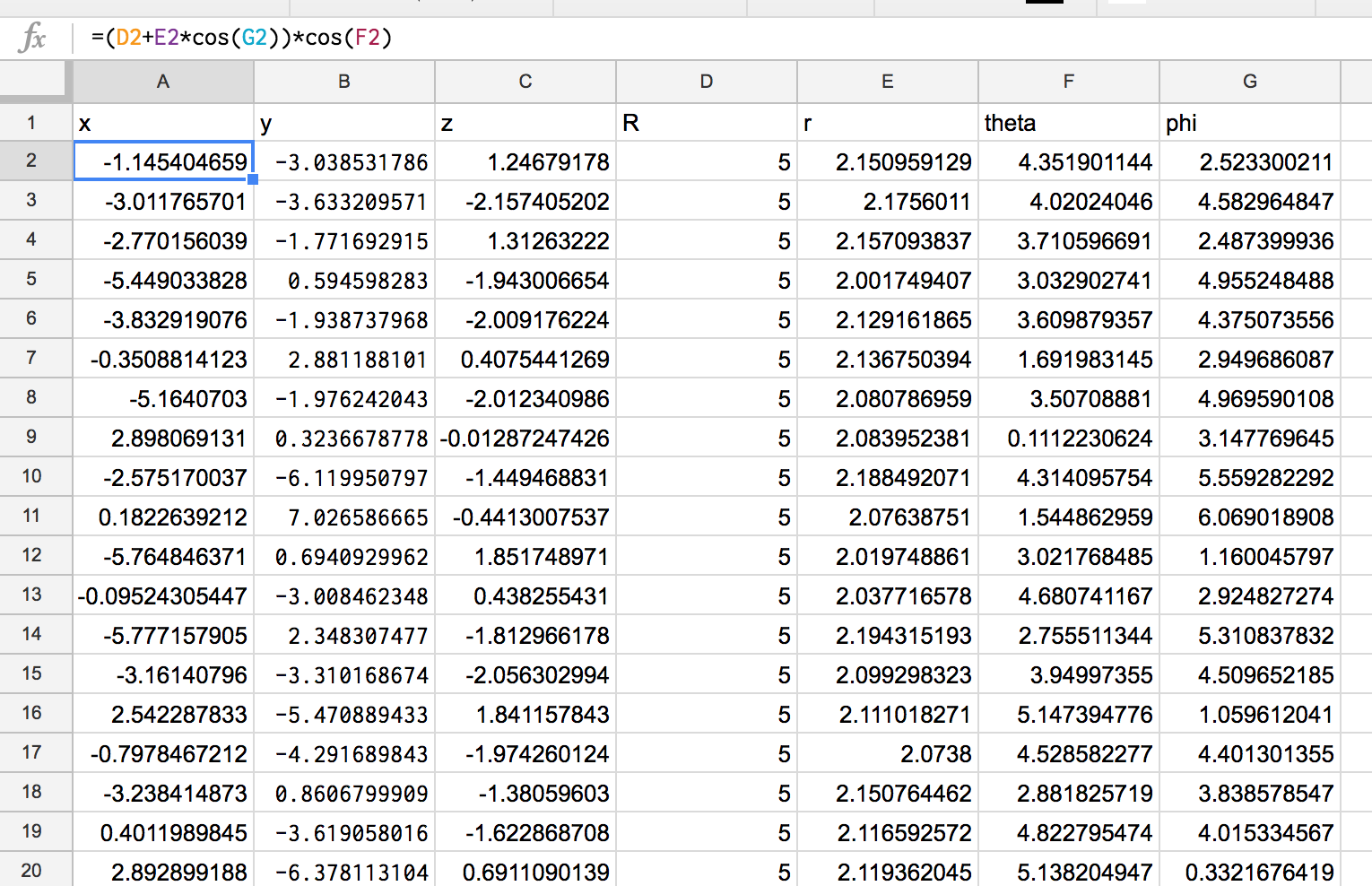
トーラス
x = (R+r \cos(\varphi))\cos(\theta) \\
y = (R+r \cos(\varphi))\sin(\theta) \\
z = r\sin(\varphi)
と、
R=5、r = 2+.2*rand()
をあわせて、spreadsheetで1000dataを生成
snippet
$T^2$の場合
data名はd_torus
d_torus %>>% (.[1:1000,]) %>>% (select(., x, y, z)) %>>% (alphaComplexDiag(.)) %>>% (.[["diagram"]]) %>>% (plot(., diagLim=c(0,10), rotated=F))
RStudioにて。
libraryはTDAに加えてdplyrとpipeRとを使用。
pipeRの2つめの部分(.[1:1000,])で使用するデータ量を選択。
例えば、(.[1:10,])とすれば、最初の10行をサンプルとしてPersistent Homologyを計算。
結果
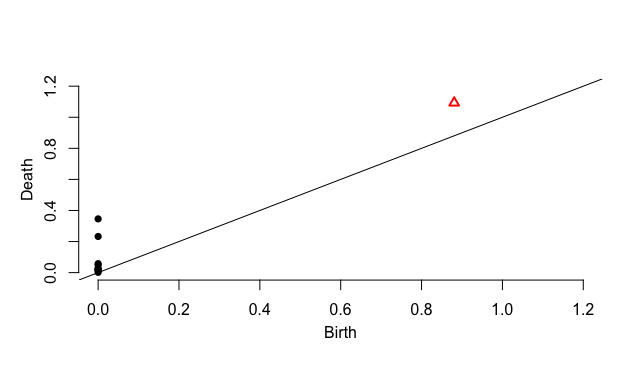
出力はpersistent diagramで。
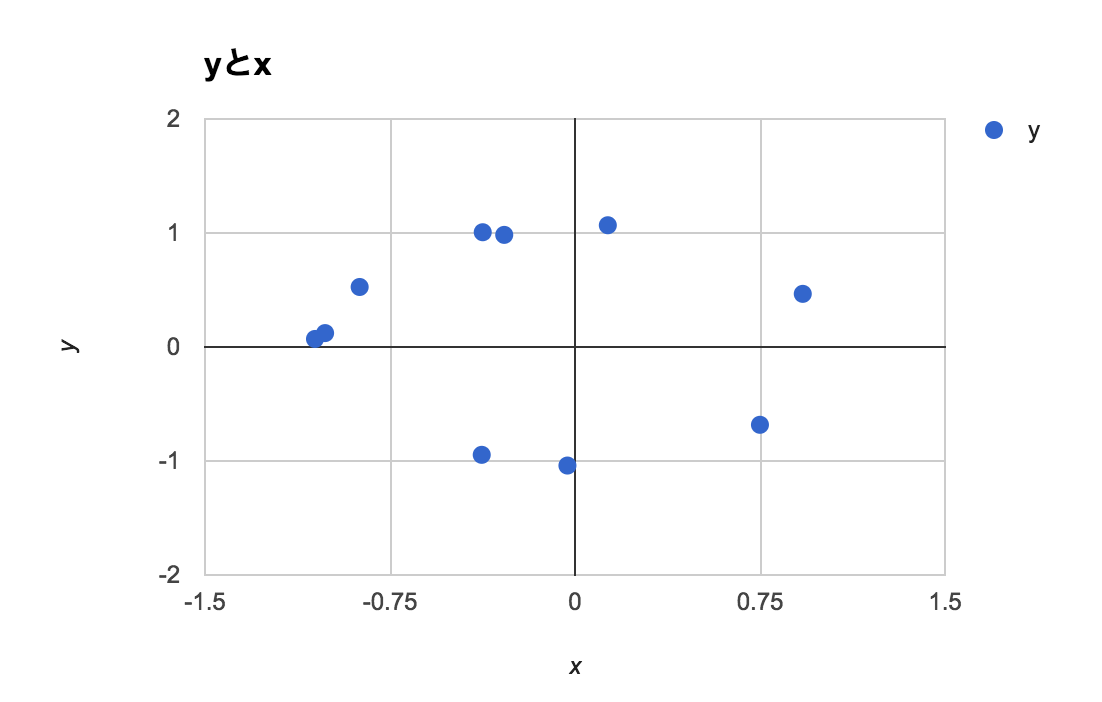
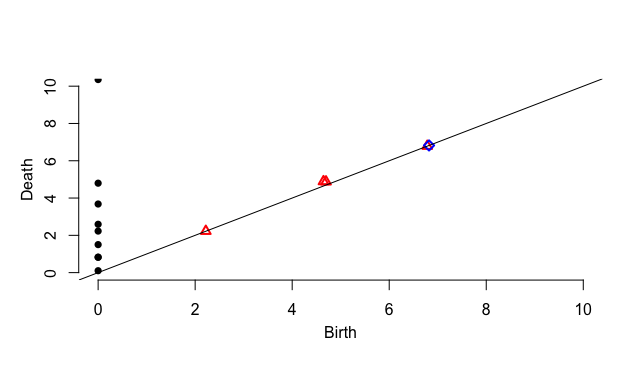
円周
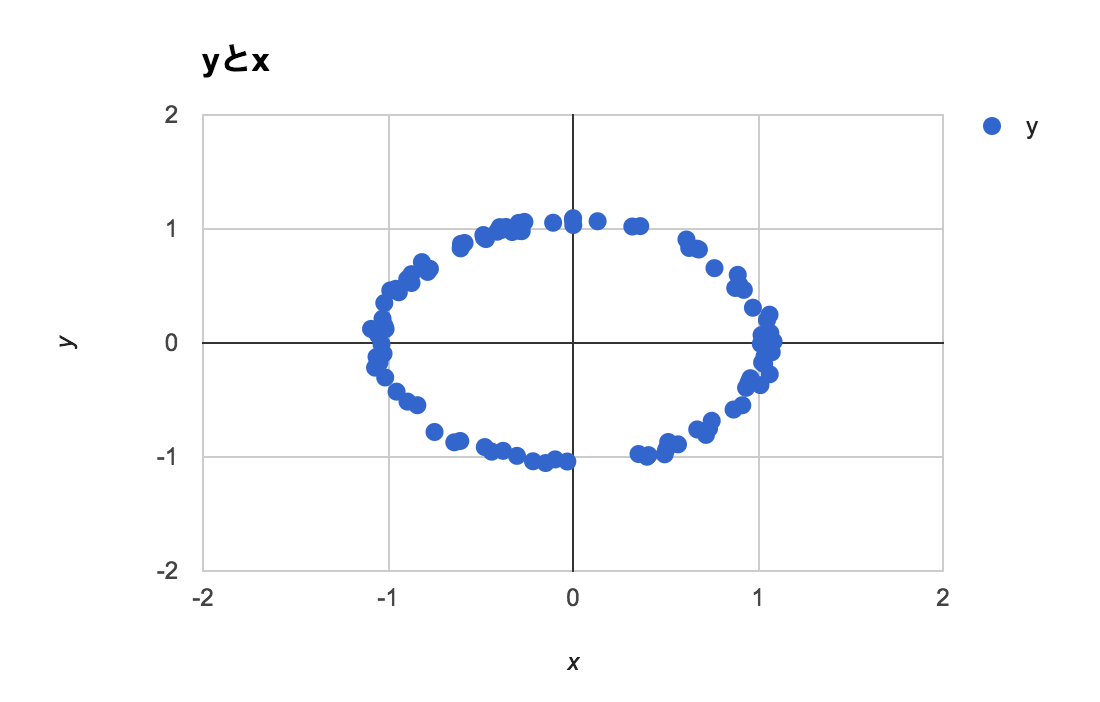
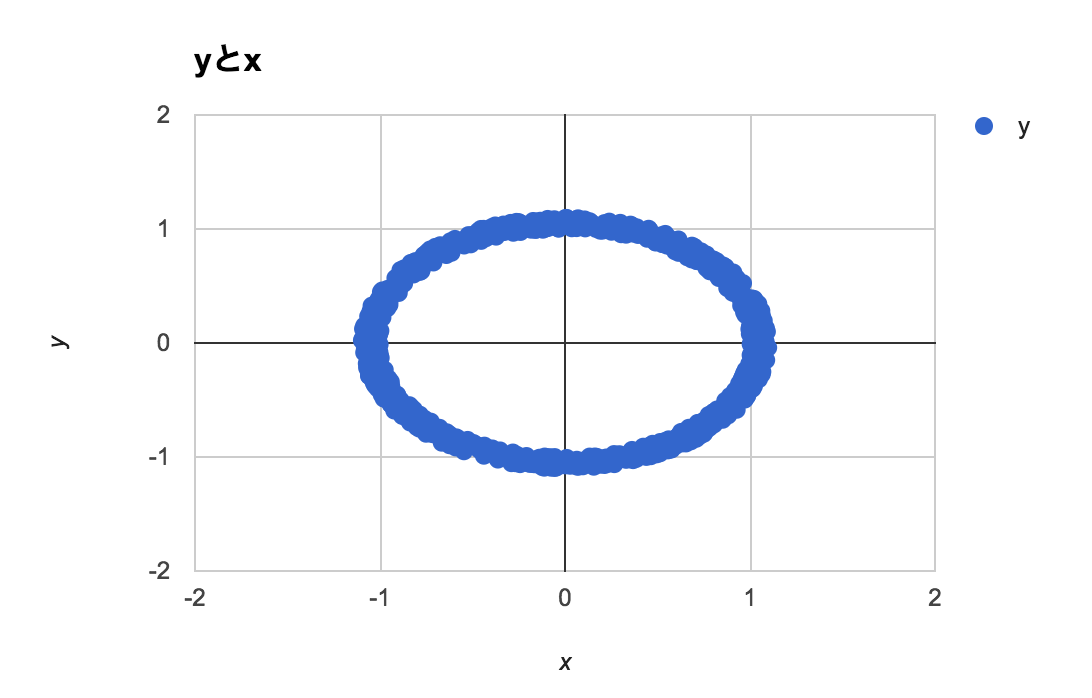
それぞれ、10点、100点、1000点での散布図とpersistent diagramを。
10点
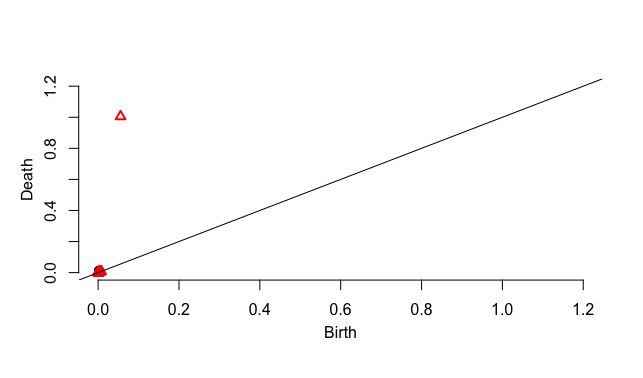
100点
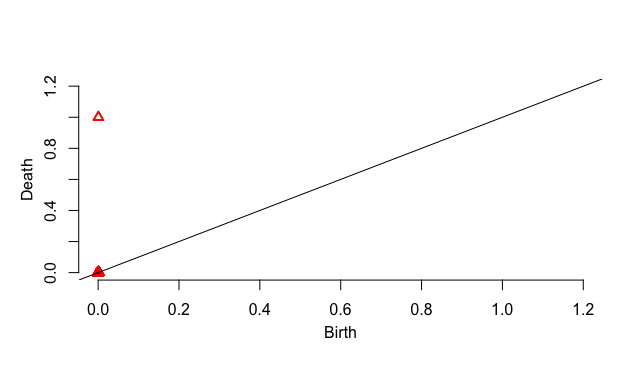
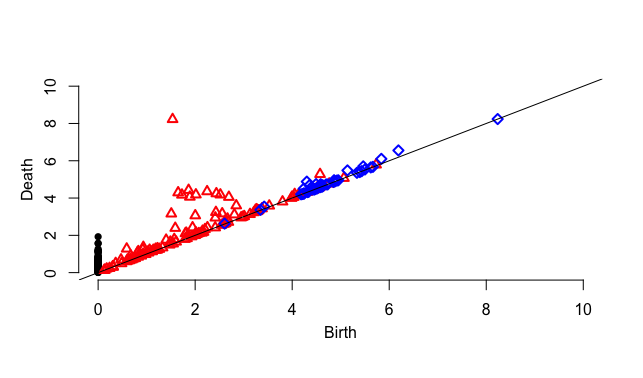
1000点
講評
10点だけだと、$S^1$と認識するのはかなり厳しい。
単純にdeath - birth$b_1 = 1$と評するためには連結成分が複数あることを認めなければならなさそう。
100点以上あれば、明らかに半径1程度の円でありそうであることを認めて良さそう。
100点から1000点になると、1次元のホモロジー類の生成のタイミングが早いことが見て取れる。
トーラス
spreadsheetで立体的な出力ができなかったので、こちらはpersistent diagramのみ
10点
100点
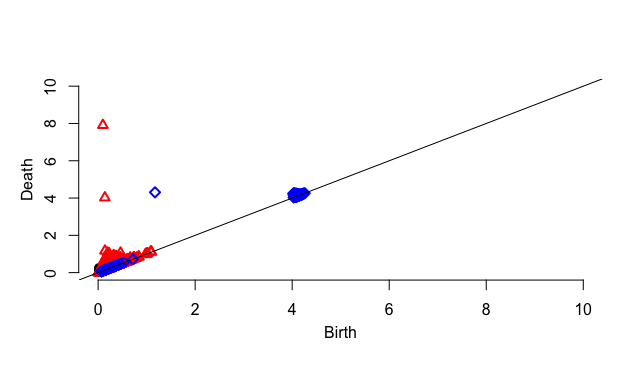
1000点
講評
1000点あれば、$b_0 = 1, b_1 = 2, b_2 = 1$の$T^2$であろうことが見て取れる。
が、100点ではそういう認識をするのは厳しい。
(100点では$S^1$とhomotopy equivalentな物体に見える)
persistent homologyは、次元に呪われそうな予感がプンプンしますね。