1. 概要
先日、大西洋沖において潜水艇タイタンが深海において遭難する事故が発生したことは記憶に新しい。事故原因についての詳細は不明であるが、深海での水圧に耐えられずに潜水艇は圧潰したのではないかと言われている。
そこで、今回は流体力学的観点から、深海において気泡の爆縮が発生するとどのようになるのかをシミュレーションを行った。
なお、計算に際してはいくつかの仮定、モデル化を行っているがこれらの妥当性については今後、機会を見て検討して行きたいと思う。
想定した流れは、深海3000mにおける半径1mの気泡の爆縮に伴う流れである。
2. 気泡の挙動を表す方程式
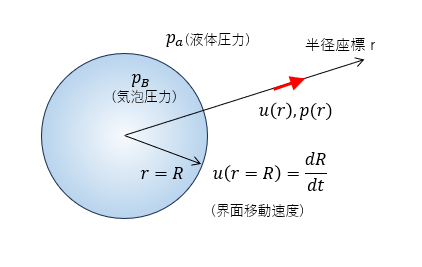
無限領域内に置かれた球(気泡)周囲の液体の流れを考える(対象とするのは、球内部ではなく球周囲の液体部分である)。液体は非圧縮性で層流とする。気泡は原点に置かれているとする。気泡周囲の流れは半径方向のみとする。
2.1. 運動方程式
気泡周囲の液体部について運動量保存式を球座標系で記述すると以下のようになる。速度成分は$r$方向のみであるから、以下のように簡略化される。
$$
\rho_l \left(\frac{\partial u}{\partial t} + u\frac{\partial u}{\partial r} \right)= - \frac{\partial p}{\partial r} + \mu_l \left[ \frac{1}{r^2}\frac{\partial}{\partial r} \left( r^2 \frac{\partial u}{\partial r} \right) -\frac{2u}{r^2} \right]
\tag{1}
$$
ここで、$t$は時間、$r$は気泡中心からの半径方向距離、$u$は半径方向速度、$\rho_l$は液体密度、$\mu_l$は液体粘度、$p$は圧力である。
2.2. 連続方程式
非圧縮性流体では質量が保存することから以下の関係式が成り立つ。
$$
u r^2 = \dot{R} R^2 = \frac{d R}{dt}R^2
\tag{2}
$$
$R(t)$は気泡の半径である。変形すると
$$
u(r,t) = \frac{R^2 \dot{R}}{r^2}
\tag{3}
$$
非回転流れであることから速度ポテンシャルが存在する。
半径方向速度は速度ポテンシャル$\Phi$を使い、$u=\frac{\partial \Phi}{\partial r}$と表されることから
$$
\Phi = \frac{-R^2 \dot{R}}{r^2}
\tag{4}
$$
(1)式右辺の粘性項は(3)式を使うと相殺されてゼロになる。従って最終的に(1)式は以下のようになる。
$$
\rho_l \left[ \frac{\partial}{\partial r} \left(\frac{\partial\Phi}{\partial t}\right)+ \frac{\partial}{\partial r} \left(\frac{u^2}{2}\right) \right] +\frac{\partial p}{\partial r} =0
\tag{5}
$$
この式を$r$について積分すると、非定常ベルヌイ式が得られる。$F(t)$は積分定数である。
$$
\rho_l \left[ \frac{\partial\Phi}{\partial t}+ \frac{u^2}{2} \right] +p =F(t)
\tag{6}
$$
$r\rightarrow \infty$の場合、$\Phi=0,p=p_\infty$であることから $F(t)=p_\infty$となる。従って
$$
p=p_\infty - \rho_l \left( \frac{\partial\Phi}{\partial t}+\frac{u^2}{2} \right)
\tag{7}
$$
(4)式を代入すると
$$
p(r,t)=p_\infty - \rho_l \left[ -\frac{R^2\ddot{R}}{r}-\frac{2R\dot{R}^2}{r}+\frac{\dot{R}^2R^4}{2r^4} \right]
\tag{8}
$$
(8)式において$r=R(t)$とすると、以下のRayleigh 方程式が得られる。
$$
R\ddot{R}+\frac{3}{2}\dot{R}^2=\frac{p_a-p_\infty}{\rho_l}
\tag{9}
$$
ここで $p_a$は、液体-気泡界面における液体側圧力である。
2.3. Rayleigh-Plesset方程式
気泡表面での液体側応力は次式で表される。
\begin{align}
\sigma_{rr}&=-p_a + 2\mu\frac{\partial u}{\partial r}-\frac{2}{3}\mu\left( \frac{\partial u}{\partial r}+\frac{2u}{r} \right) \\
&=-p_a+\frac{4\mu}{3} \left( \frac{\partial u}{\partial r} - \frac{u}{r} \right)
\end{align}
\tag{10}
ここで$\partial u/\partial r$は次式で表される。
$$
\frac{\partial u}{\partial r}=\frac{\partial}{\partial r} \left(\frac{R^2\dot{R}}{r^2} \right)= -2\frac{R^2\dot{R}}{r^3}
\tag{11}
$$
$r=R$とすると、以下の応力表現式が得られる。
$$
\sigma_{rr}(r=R)=-p_a - 4\mu\frac{\dot{R}}{R}
\tag{12}
$$
気泡の表面においてラプラスの式が成り立つと仮定すると
$$
p_B+\sigma_{rr}=\frac{2S}{R}
\tag{13}
$$
ここで $S$は気液界面での表面張力である。
液体-気泡界面における気体側圧力を $p_B$とすると、界面における力の釣り合いから次式が成り立つ。
$$
p_a = p_B - 4\mu_l \frac{\dot{R}}{R} - \frac{2S}{R}
\tag{14}
$$
気泡圧力$p_B$を使ってRayleigh方程式を整理すると以下のRayleigh-plesset方程式が得られる。
$$
\frac{p_B-p_\infty}{\rho_l} = R\ddot{R}+\frac{3}{2}\dot{R}^2+\frac{4\mu_l}{\rho_l}\frac{\dot{R}}{R}+\frac{2S}{\rho_l R}
\tag{15}
$$
気泡が極めて短い時間で爆縮する場合、気泡内外での熱の移動は起こらないとみなしてもよい。気泡内部では均一の圧力になっていると仮定すると、気泡半径$R$と気泡圧力$p_B$には以下の等エントロピー関係式が成り立つ。
$$
\frac{p_B}{p_{B0}}=\left(\frac{V_0}{V}\right)^\gamma=\left(\frac{R_0}{R}\right)^{3\gamma}
\tag{16}
$$
ここで、$V,R$はそれぞれ、気泡体積、気泡半径を表しており、添字ゼロは初期値を表している。$\gamma$は比熱比である。
これらの式を組み合わせると最終的に$R$に関する二階常微分方程式が得られる。
$$
R\ddot{R}+\frac{3}{2}\dot{R}^2+\frac{4\mu_l}{\rho_l}\frac{\dot{R}}{R}+\frac{2S}{\rho_l R}-\frac{1}{\rho_l}\left[ p_{B0}\left( \frac{R_0}{R} \right)^{3\gamma} - p_\infty \right]=0
\tag{17}
$$
液相内の圧力の空間分布は次式で表される。
$$
p(r,t)=p_\infty\left[ 1-\frac{R}{r} \right]
+p_B\frac{R}{r}
-\frac{2}{r}(2\mu\dot{R}+\sigma)
+\rho_l\frac{R\dot{R}^2}{2r}\left[1-\frac{R^3}{r^3} \right]
\tag{18}
$$
3. Juliaを使った気泡挙動の計算
3.1. 連立一階常微分方程式
Rayleigh-plesset方程式は、二階常微分方程式となっているため連立一階常微分方程式に変換して計算を行った。以下に連立微分方程式を示す。
\begin{align}
\frac{d R}{d t}&=U
\tag{19} \\
\frac{d U}{d t}&=
\frac{1}{R}\left[
\frac{1}{\rho_l}\left\{ p_{B0}\left( \frac{R_0}{R} \right)^{3\gamma} - p_\infty \right\}
-\frac{3}{2}U^2-\frac{4\mu_l}{\rho_l}\frac{U}{R}-\frac{2S}{\rho_l R}
\right]
\tag{20}
\end{align}
ここで、$R$:気泡半径、$U$:気泡界面の速度(外向きを正)、$\rho_l$:液体密度(=1000[kg/m^3])、$\mu_l$:液体粘度(=1e-3[Pa.s])、$S$:表面張力係数(=0.07[N/m])、$\gamma$:比熱比(=1.4)、$p_{B0}$:初期気泡圧力(=大気圧=1e5[Pa])、$p_\infty$:気泡周囲の液相圧力(=3e7[Pa])、$R_0$:初期気泡半径(=1[m])
3.2. 解析プログラム
常微分方程式を計算するためにJuliaを使用した。式中に含まれるパラメータは、深度3000mにおける、半径1[m]の球形気泡を想定した。なお気泡内部は人間が滞在できる環境を想定し20℃、大気圧の空気とした。具体的な数値は以下のプログラムリストに記述している。解析は時刻ゼロにおいて水深3000[m]に配置した球形気泡が爆縮する様子を計算する。
using ParameterizedFunctions, DifferentialEquations
using Plots
using Printf
# 常微分方程式の定義
eqns = @ode_def bubble begin
dR = V
dV = ((patm*(Rini/R)^(3.0*gamma)-pinf)/rhoL-1.5*V^2-4.0*nuL*V/R-2.0*sigma/(rhoL*R))/R
end patm pinf Rini rhoL nuL gamma sigma
patm = 1e5 # [Pa]
pinf = 3e7 # [Pa]
rho0 = 1.2 # [kg/m3]
Tini = 293.0 # [K]
Rini = 1.0e-0 # [m]
rhoL = 1000.0 # [kg/m3]
nuL = 1e-6 # [m2/s]
gamma = 1.4 # [-]
sigma = 0.07 # [N/m]
# 問題定義
u0 = [Rini; 0.0] # 初期 R, V
tspan = (0.0, 1e-2) # 時間積分期間
p = [ patm, pinf, Rini, rhoL, nuL, gamma, sigma ]
prob = ODEProblem(eqns,u0,tspan,p)
# 計算
@time sol = solve(prob,Tsit5(),reltol=1e-8,abstol=1e-8)
(nrow,ncol)=size(sol)
times=zeros(Float64,0)
radis=zeros(Float64,0)
velos=zeros(Float64,0)
press=zeros(Float64,0)
temps=zeros(Float64,0)
@printf("j : time radi velo pres rho temp\n")
for j=1:ncol
time = sol.t[j]
radi = sol.u[j][1]
velo = sol.u[j][2]
pres = patm*(Rini/radi)^(3.0*gamma)
rho = rho0*(Rini/radi)^3.0
temp = Tini*(Rini/radi)^(3.0*(gamma-1.0))
append!(times,time)
append!(radis,radi)
append!(velos,velo)
append!(press,pres)
append!(temps,temp)
@printf("j=%d : %16.8e %16.8e %16.8e %16.8e %16.8e %16.8e\n",
j,time,radi,velo,pres,rho,temp)
end
p1 = plot(times, radis, title="history of radius[m]",
legend=:bottomleft, linewidth=1, linestyle=:solid,
xlabel="time[sec]", ylabel="r[m]", label="radius" )
savefig("radi.png")
p2 = plot(times, velos, title="history of velocity[m/s]",
legend=:bottomright, linewidth=1, linestyle=:solid,
xlabel="time[sec]", ylabel="v[m/s]", label="velocity" )
savefig("velo.png")
p3 = plot(times, press, title="history of pressure[Pa]",
legend=:topleft, linewidth=1, linestyle=:solid,
xlabel="time[sec]", ylabel="p[Pa]", label="pressure" )
savefig("pres.png")
p4 = plot(times, temps, title="history of temperature[K]",
legend=:topright, linewidth=1, linestyle=:solid,
xlabel="time[sec]", ylabel="T[K]", label="temperature" )
savefig("temp.png")
plt = plot(p1, p2, p3, p4; layout=(4,1), size=(640, 960) )
savefig("all.png")
3.3. 解析結果
計算結果によれば気泡半径は周期的に増減を繰り返し、またそれに付随して、気泡界面速度、圧力、温度も周期的に増減を繰り返していることがわかった。
今回の計算では気泡が崩壊、移動する影響は考慮していないため、長期間に渡ってこのような振動する解になっているが、実際の現象は最初の振動ピーク時刻の手前において気泡は破壊するものと考えられる。
以下に時刻 0から0.01[秒]までの結果図を示す。
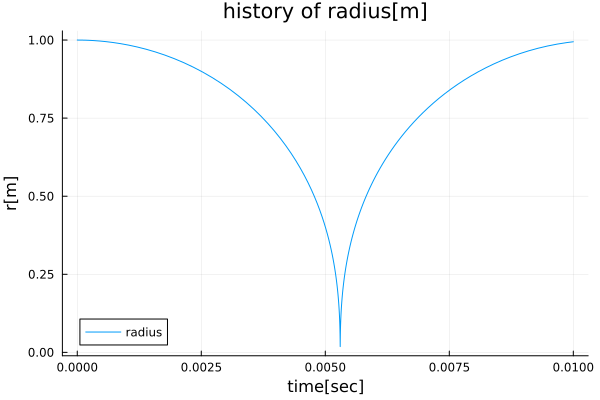
3.3.1. 気泡の半径$R$
以下に気泡半径の経時変化を示す。気泡半径は初期値1.0[m]から時間と共に減少し、時刻$t=5.3\times10^{-3}[sec]$で最小値$R=1.84\times10^{-2}[m]$となる。その後、動きが反転し半径は時間と共に増大するような結果となった。
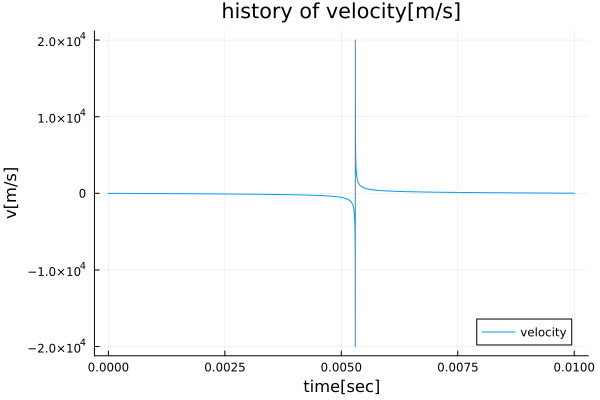
3.3.2. 気泡界面の速度
気泡半径が増減することから、気泡界面速度は周期的に符号が反転している。ピークとなる流速絶対値は$O(10^4)$となっており、実際にはこのようなピークは発生しないと考えられる。
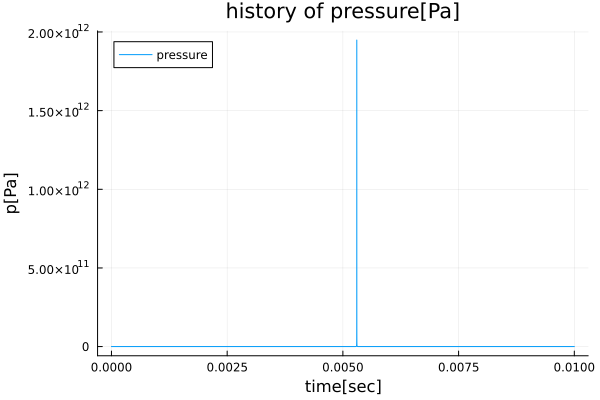
3.3.3. 気泡の圧力
気泡の圧力は気泡半径が最小となる時刻において最大となっている。ただし圧力のピーク値は$O(10^{12})$[Pa]となっており非現実的な値となっている。
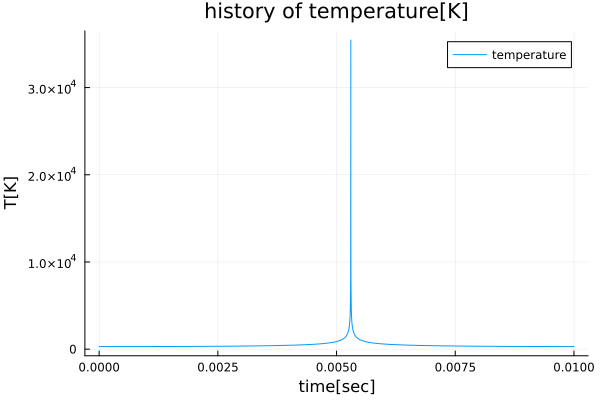
3.3.4. 気泡の温度
気泡の温度は気泡半径が最小となる時刻において最大となっている。ただし温度のピーク値は$O(10^{4})$[K]となっており非現実的な値となっている。
3.3.5. 圧力の空間分布
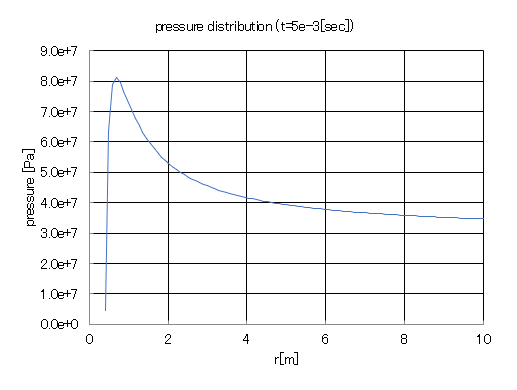
時刻$t=5\times10^{-3}[sec]$における圧力の空間分布を示す。
この図は気泡半径$R(=0.402[m])$から$r=10[m]$の範囲の圧力分布を示している。気泡表面付近において圧力が急激に上昇していることがわかる。
4. 結論
潜水艇タイタンの事故で発生したと思われる爆縮現象のシミュレーションを行ってみた。計算結果によれば、気泡半径は時刻t=5.3[msec]で最小値1.8[cm]程度となった。しかし、この時刻では速度、圧力、温度は非現実的な値となっており、実際にはもっと早い時点で気泡は崩壊していると想像される。
今回の計算では、不自然な仮定も含まれているが、今後の調査、研究の何らかの参考になれば幸いである。
参考:こちらでは 数値流体力学 を使った流れ計算 も行われているようである。