はじめに
OpenFOAMでメッシュを作成する場合、OpenFOAM付属のメッシャーとして
- blockMesh
- snappyHexMesh
が利用可能です。 blockMeshは構造格子タイプのメッシュを組み合わせる(すなわち領域をブロッキングする)ことで任意の形状にも対処できるようになっています。しかし、形状が複雑になってくると形状をブロッキングするのは難しいため、複雑な形状は必然的にsnappyHexMeshなどを使いメッシュを作成することになります。このような事情もあって、最近はblockMeshを使用していなかったのですがOpenFOAMの例題を見てみるとblockMeshが想像以上に使い易くなっていたので紹介します
形状エンティティに名前をつけることができる
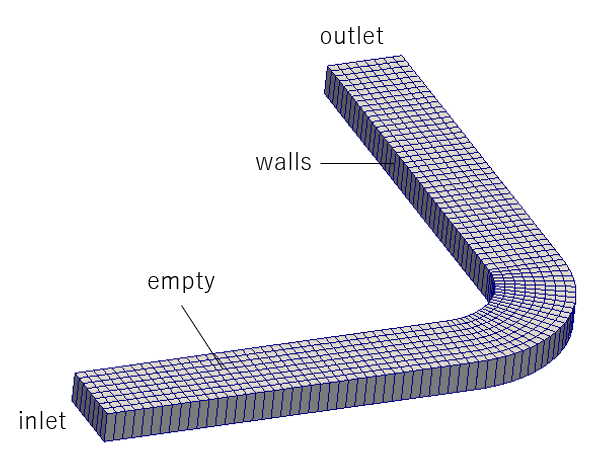
これは、自分が知らなかっただけで以前から存在していた機能かもしれません。現在のblockMeshDict辞書では、vertices、blocksなどに名前を付けてその形状を参照することができます。例えば、二次元のエルボー管の例を示します。
/*--------------------------------*- C++ -*----------------------------------*\
| ========= | |
| \\ / F ield | OpenFOAM: The Open Source CFD Toolbox |
| \\ / O peration | Version: v2206 |
| \\ / A nd | Website: www.openfoam.com |
| \\/ M anipulation | |
\*---------------------------------------------------------------------------*/
FoamFile
{
version 2.0;
format ascii;
class dictionary;
object blockMeshDict;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
// パラメータの定義
nl1 40;
nc 24;
nl2 40;
nw 8;
zmin -0.2;
zmax 0.2;
width 1.0;
length1 5.0;
length2 5.0;
radius 1.0;
angle 90;
// 頂点(vertex)の座標値の定義
xi1 #eval{ -$length1 };
yi1 #eval{ -$radius };
xi2 #eval{ $xi1+$length1 };
yi2 #eval{ $yi1 };
xi3 #eval{ $radius*sin(degToRad($angle)) };
yi3 #eval{-$radius*cos(degToRad($angle)) };
xi4 #eval{ $xi3+$length2*cos(degToRad($angle)) };
yi4 #eval{ $yi3+$length2*sin(degToRad($angle)) };
xo1 #eval{ -$length1 };
yo1 #eval{ -($radius+$width) };
xo2 #eval{ $xo1+$length1 };
yo2 #eval{ $yo1 };
xo3 #eval{ ($radius+$width)*sin(degToRad($angle)) };
yo3 #eval{-($radius+$width)*cos(degToRad($angle)) };
xo4 #eval{ $xo3+$length2*cos(degToRad($angle)) };
yo4 #eval{ $yo3+$length2*sin(degToRad($angle)) };
// 頂点(vertex)の定義
vertices
(
name vi1 ($xi1 $yi1 $zmin)
name vi2 ($xi2 $yi2 $zmin)
name vi3 ($xi3 $yi3 $zmin)
name vi4 ($xi4 $yi4 $zmin)
name vo1 ($xo1 $yo1 $zmin)
name vo2 ($xo2 $yo2 $zmin)
name vo3 ($xo3 $yo3 $zmin)
name vo4 ($xo4 $yo4 $zmin)
name vi1e ($xi1 $yi1 $zmax)
name vi2e ($xi2 $yi2 $zmax)
name vi3e ($xi3 $yi3 $zmax)
name vi4e ($xi4 $yi4 $zmax)
name vo1e ($xo1 $yo1 $zmax)
name vo2e ($xo2 $yo2 $zmax)
name vo3e ($xo3 $yo3 $zmax)
name vo4e ($xo4 $yo4 $zmax)
);
blocks
(
name inblk hex (vi1 vo1 vo2 vi2 vi1e vo1e vo2e vi2e) ($nw $nl1 1) grading (1 1 1)
name crvblk hex (vi2 vo2 vo3 vi3 vi2e vo2e vo3e vi3e) ($nw $nc 1) grading (1 1 1)
name outblk hex (vi3 vo3 vo4 vi4 vi3e vo3e vo4e vi4e) ($nw $nl2 1) grading (1 1 1)
);
edges
(
arc vi2 vi3 origin (0 0 $zmin)
arc vo2 vo3 origin (0 0 $zmin)
arc vi2e vi3e origin (0 0 $zmax)
arc vo2e vo3e origin (0 0 $zmax)
);
defaultPatch
{
name empty;
type empty;
}
boundary
(
walls
{
type patch;
faces
(
(inblk 0)
(inblk 1)
(crvblk 0)
(crvblk 1)
(outblk 0)
(outblk 1)
);
}
inlet
{
type patch;
faces ((inblk 2)); // faces ((0 4 12 8));
}
outlet
{
type patch;
faces ((outblk 3)); // faces ((7 3 11 15));
}
);
// ************************************************************************* //
このblockMeshDictを使い作成したメッシュは以下のようになります
verticesの記述を見ると (x,y,z)座標値の前に名前が追加されているのがわかります。例えば
以下の例ではvi1という名前で頂点を定義しています。
vertices
(
name vi1 ($xi1 $yi1 $zmin)
...
またブロックの定義では、頂点名を参照して新しくinblkという名前のブロックを作成していることがわかります
blocks
(
name inblk hex (vi1 vo1 vo2 vi2 vi1e vo1e vo2e vi2e) ($nw $nl1 1) grading (1 1 1)
...
場合によっては、エンティティを定義する際に、数字ではなく名前を使うようにしたほうがわかりやすいかもしれません。
面(face)を定義する際に、ブロック名+面番号が使用できる
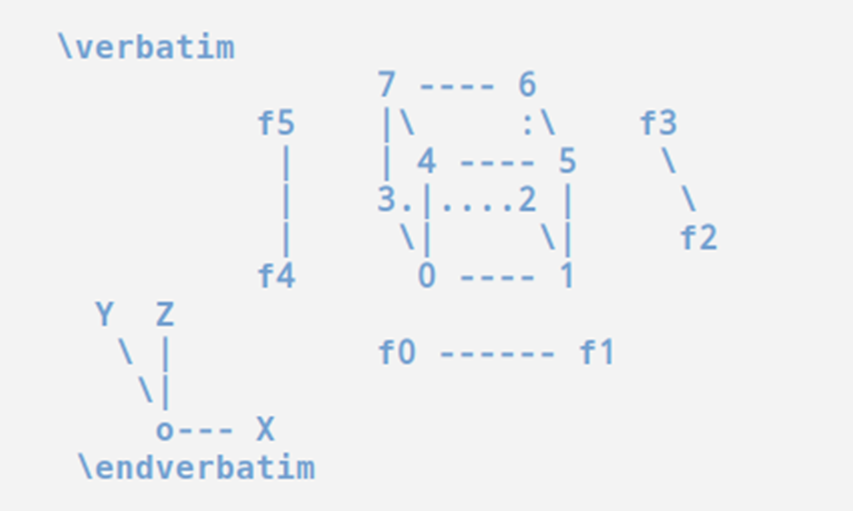
境界面を定義する場合、面を構成する4頂点を指定しますが、代わりの方法としてブロック名(あるいはブロック番号)と面番号を定義する方法も使用できます。ここで面番号とはブロックを構成する6面に対して定義されるものであり、頂点の並びに従って自動的に場所が特定されます。マニュアルを見ればこの規約が書かれていると思いますが、blockMesh -help と実行することで、以下のようにヘルプメッセージとして図示することが可能です(f0~f5が面番号)。ブロックの8頂点にかかれている数字がブロック構成頂点番号です。
blockMesh -help
上に示したblockMeshDictの例だと境界面の定義は以下のようになっています。なお、従来の方法に従い4頂点の並びで面を定義しても構いません(混在も可)。面番号を使えば、境界上の頂点並び順を気にしなくてもよいため、わかりやすいかもしれません。
boundary
(
walls
{
type patch;
faces
(
// (ブロック名あるいはブロック番号 面番号)
// 以下の inblkは最初に定義されたブロックなのでブロック番号=0としても可
(inblk 0)
(inblk 1)
(crvblk 0)
(crvblk 1)
(outblk 0)
(outblk 1)
);
}
inlet
{
type patch;
faces ((inblk 2)); // faces ((0 4 12 8));
}
outlet
{
type patch;
faces ((outblk 3)); // faces ((7 3 11 15));
}
);
頂点番号を図表示することができる
blockMeshコマンドを実行する際に -write-vtk オプションを指定することでblockMeshDictのブロッキング定義状態を可視化することができます。実際に図を見てもらったほうがわかりやすいかと思いますので以下に示します。
blockMesh -write-vtk
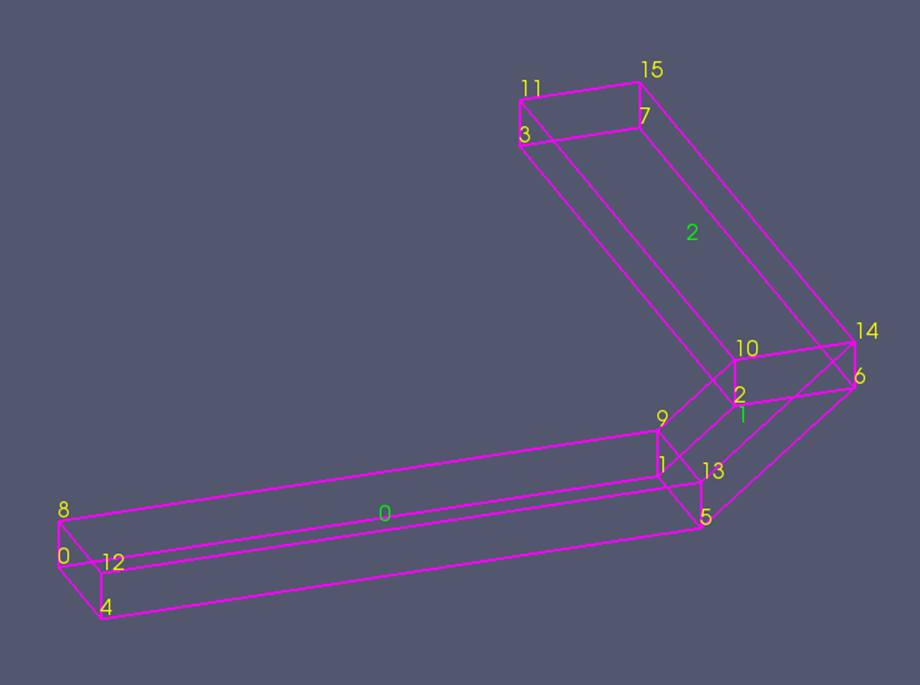
これにより blockTopology.vtuおよび blockFaces.vtp という名前のファイルが作成されます。paraviewを起動し、blockTopology.vtuファイルを読み込みます。次にすべての表示セルを選択します。その後、find dataボタンを押し、 cell ID、point ID を表示するように指定します。
すべての表示セルを選択(予めワイヤーフレーム表示にしておく)

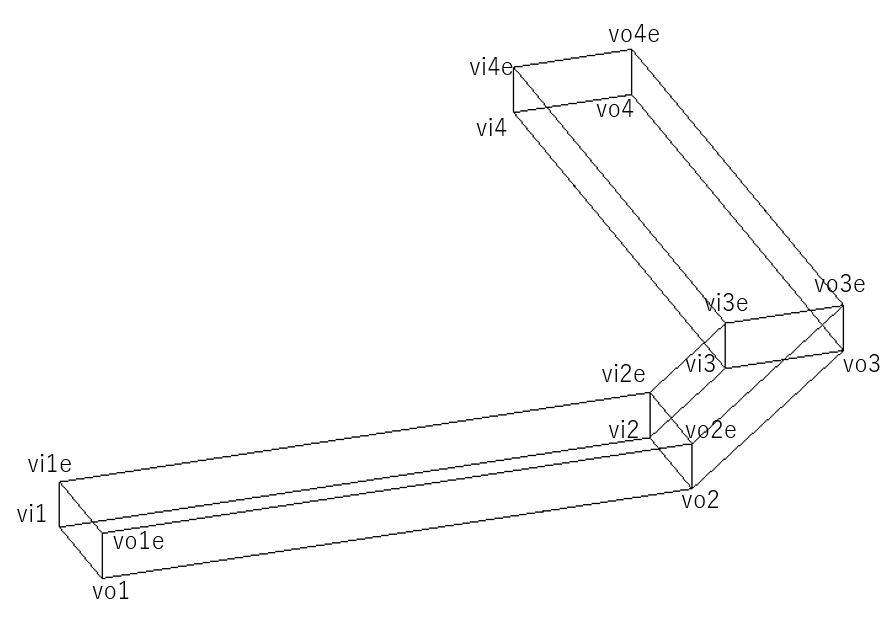
参考までに頂点名で表示した図も示しておきます
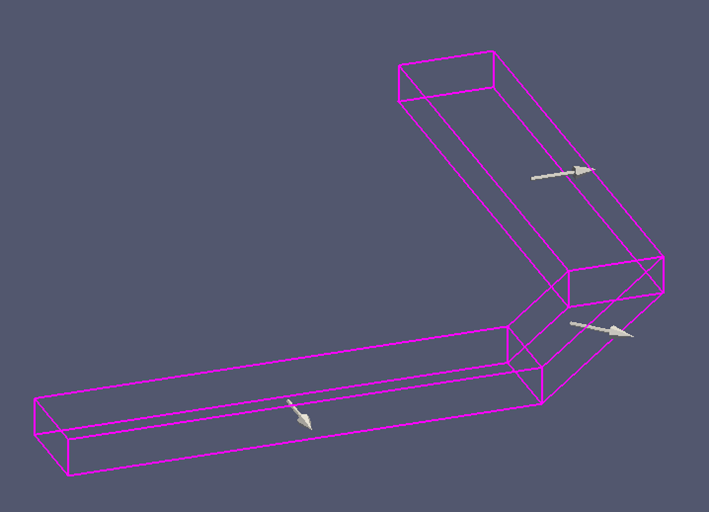
ブロックの配置方向を矢印で表示できる
ブロックには頂点配置により配置方向が決まります。この配置方向をベクトル図として表示することができます。
ベクトルを適当に選ぶ(ここではlocal-direction0)
このように図示することでブロックの方向(および面の位置)が容易に把握できるようになります。
まとめ
blockMeshを便利に使うためのいくつかのtipsを紹介しました。何らかの参考になれば幸いです。