はじめに
ここに載せるコードはプログラミングを初めて3ヶ月ほどの時に書き、書いてから1年ほど経つが、それをまとめておこうと思う。言語はfortran。
使う人が少ない言語だと思うが、アルゴリズムは同じなので誰かの役に立つといいなぁ...
ここでは簡単な三次方程式の解をニュートン法と二分法を用いて近似的に求めるプログラムを載せておく。
なお、この記事では数学的に厳密な説明をしていません。
また、このサイトを参照したことによって生じたいかなる損害やトラブルの責任は一切負いかねますので予めご了承ください(^^)/
ニュートン法とは
ニュートン法とは、簡単に言うと方程式の解を近似的に求める方法。
手で解けない方程式を数値的に解く際によくこの方法が用いられる。
ニュートン法の具体的な方法
ニュートン法は以下の図のようにして近似的に方程式 f(x) = 0 の解(赤点)を求めていく。
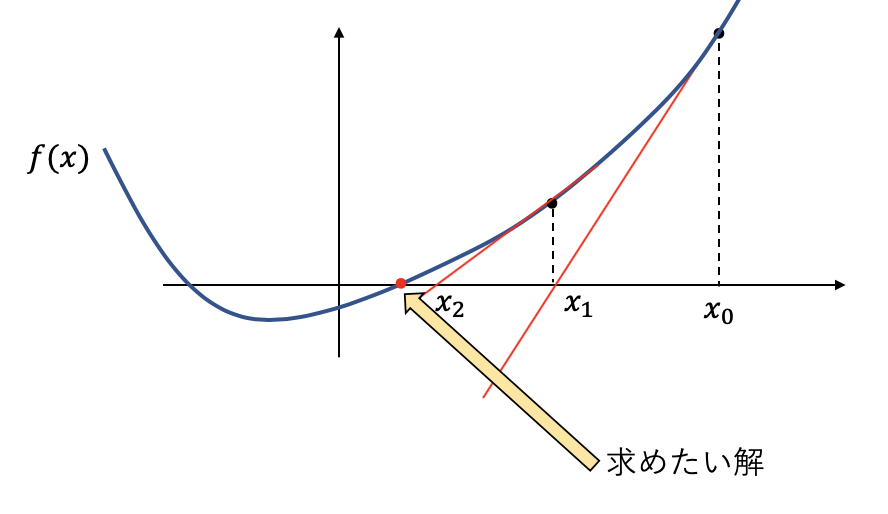
まず、適当な位置に開始位置 $x_0$ を定め、$x = x_0$ においての接線を求める。
その接線とx軸との交点を $x_1$ として同様に $x = x_1$ での接線を求め、そのx軸との交点を $x_2$ とする。
以上のことを繰り返し、n本目の接線とn+1本目の接線のx軸との交点の差 $|x_n - x_{n+1}|$ の値が小さくなれば、そのx座標を方程式の解とみなし計算を終了する。
また、今回の図ではもう1つ解が存在する。
それを求めるためには、最初に与えるx座標の値を的確に小さくして同様に計算すれば良い。
二分法とは
二分法は以下の図のようにして近似的に方程式 f(x) = 0 の解を求めていく。
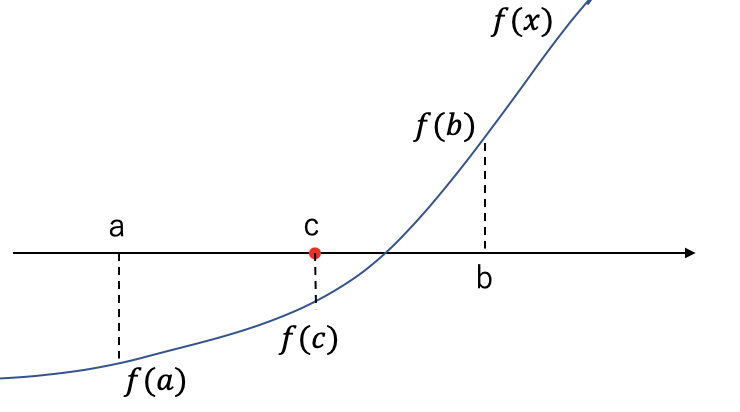
まず最初に適当なx座標の値 $a, b$ を(解を挟むように)2つ与える。
ここで、$c = (a + b)/2$ として、$f(c)$ の正負を考える。
(1)もし、$f(c)<0$ ならば関数が単調に増加する場合、方程式の解は$c$よりも大きい。
したがって、$c$ を $a$ に置き換えて新たに $c$ を求める。
(2)もし、$f(c)>0$ ならば関数が単調に増加する場合、方程式の解は$c$よりも小さい。
したがって、$c$ を $b$ に置き換えて新たに $c$ を求める。
図の場合、$f(c)<0$ から、方程式の解はcの右側にあるので、(1)が該当する。
以上を繰り返し、$f(c)$ の値が任意の値よりも小さくなれば計算終了とし、方程式の解を近似的に求めることができる。
実装
ここに簡単な三次方程式の解を求めるプログラムを載せておく。
もっとこう書いた方が良い!!などありましたら教えてくださると幸いです。
module functions_module
implicit none
contains
double precision function func(x) !func: 解を求めたい関数
double precision, intent(in)::x
func = x**3 - 2.d0*x**2 - x + 2.d0
end function func
double precision function dfunc(x) !dfunc: funcの導関数
double precision, intent(in) :: x
dfunc = 3.d0*x**2 - 4.d0*x - 1.d0
end function dfunc
end module functions_module
!--------メインプログラム--------------------
program newton
use functions_module
implicit none
integer::i, j
real(8):: a, b, c
real(8):: xold1, xold2, xnew1, xnew2 !xold:計算開始するx座標,xnew:新たに求まったx座標(接線との交点)
real(8), parameter :: eps = 1.0d-5 !誤差
xold1 = -5.d0 !初期値
xold2 = 5.d0
!---------------2つor1つの解を求める(ニュートン法)--------
i = 0
do
i = i + 1
xnew1 = xold1 - func(xold1)/dfunc(xold1)
if (abs(xnew1 - xold1) < eps) exit
xold1 = xnew1
if (i == 100) then
exit
end if
end do
j = 0
do
j = j + 1
xnew2 = xold2 - func(xold2)/dfunc(xold2)
if (abs(xnew2 - xold2) < eps) exit
xold2 = xnew2
if (j == 100) then
xnew2 = xnew1
exit
end if
end do
if (i == 100) then
xnew1 = xnew2
end if
if (xnew1 /= xnew2) then
print *, xnew1, xnew2
else
print *, xnew1
end if
!------3つ目の解( c )を求める(二分法)-----------
a = xnew1 + eps
b = xnew2 - eps
if ((xnew1 /= xnew2).AND.(func(a)*func(b)<0)) then
do while((func(c)>eps).OR.(abs(a-b)>eps))
c = (a + b)/2.d0
if (func(c)>0) then
a = c
else if (func(c)<0) then
b = c
else
exit
end if
end do
print *, c
end if
end program newton
三次方程式の3つの解のうち、最大のものと最小のものをニュートン法を用いて求め、残りの1つの解を二分法を用いて求めている。
また、このプログラムは、解が3つまでの方程式に対して、その導関数を与えれば方程式の解を数値的に求めるものとして書いたつもりだ。
しかし、関数によってはうまく答えが求められない場合があるかもしれない。
1つのプログラムであらゆる場合に対して処理を行うコードを書くのはなかなか難しいですね。