第0章 復習
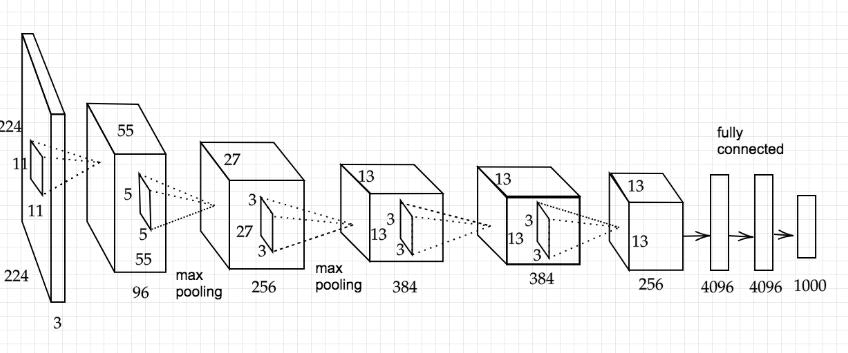
0.1 AlexNet
AlexNetとは2012年に開かれた画像認識コンペティション(ILSVRC)で、
2位(東京大学原田研究室のチーム:サポートベクターマシーンを利用)に大差をつけて優勝したモデル。
エッジやグラデーションをとらえるようなフィルタを自動で学習しているところが画期的
それまでのILSVRCでは年2%ずつのエラー改善だったが、AlexNetは一気に10%以上改善した。
AlexNetの登場で、ディープラーニングが大きく注目を集めた。
0.2 AlexNetのモデルの構造
5層の畳み込み層およびプーリング層など、それに続く3層の全結合層から構成される。
CNNの登場により、画像の縦横方向のつながりを意識しながら情報を伝達して学習を進められる。
RNNの問題
・勾配爆発
⇒学習時に層を遡るにつれて勾配が大きくなりすぎる問題
対策:勾配クリッピングなどが有効
勾配クリッピング
⇒勾配の大きさに制限をかけることで勾配爆発を抑制
勾配の$L^2$ノルムがしきい値より大きい場合、次の式により勾配を調整
$$勾配 \Longrightarrow \frac{しきい値}{L^2 ノルム}\times 勾配$$
・勾配消失
⇒勾配が小さくなりすぎる問題がある。
対策:LSTM
確認テスト:サイズ5x5の入力画像をサイズ3x3のフィルタで畳み込んだ時の出力画像のサイズを答えよ。
なおストライドは2、パディングは1とする。
答:$3\times 3$
\begin{eqnarray}
O_H&=&\frac{5+2\times 1-3}{2}+1=3\\
O_W&=&\frac{5+2\times 1-3}{2}+1=3
\end{eqnarray}
参考:公式
\begin{eqnarray}
O_H&=&\frac{(画像の高さ)+2\times (パディング)-(フィルターの高さ)}{ストライド}+1\\
O_W&=&\frac{(画像の幅)+2\times (パディング)-(フィルターの幅)}{ストライド}+1\\
\end{eqnarray}
確認テスト(追加):サイズ5x5の入力画像をサイズ5x5のフィルタで畳み込んだ時の出力画像のサイズを答えよ。
なおストライドは2、パディングは1とする。
答:$2\times 2$
\begin{eqnarray}
O_H&=&\frac{5+2\times 1-5}{2}+1=2\\
O_W&=&\frac{5+2\times 1-5}{2}+1=2
\end{eqnarray}
第1章 再帰型ニューラルネットワーク(RNN)の概念
1.1 RNNとは
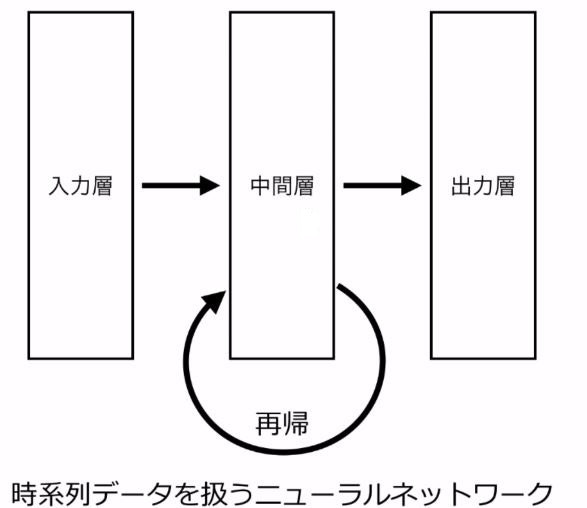
時系列データを扱うことが得意なニューラルネットワークの一種
⇒入力と正解が「時系列データ」となる。
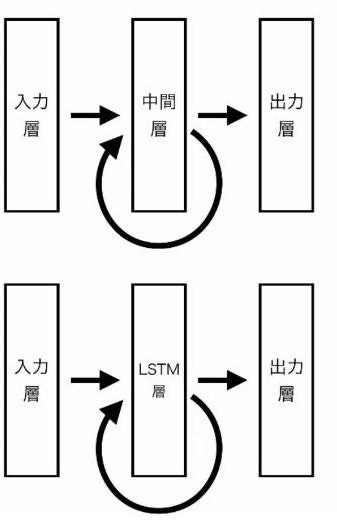
⇒中間層が再帰(Reccurent)の構造を持ち、前後の時刻の中間層を繋ぐ。
時間に遡って逆伝播が行われる。
全ての時刻の中間層で、パラメータは共有される。
1.2 時系列データ
時系列データの定義
時間的順序を追って一定時間ごとに観測され、しかも相互に統計的依存関係があるデータの系列
⇒ 時間的なつながりのあるデータ
時系列データの具体例は?
・株価のデータ(昨日の株価⇒今日の株価⇒明日の株価)
・音声データ(時間的に意味のない音声はノイズになる。時間的なつながりがある。)
・動画
・産業用機器の状態
・テキスト(単語を1つ1つをある時点のデータとして扱う。)
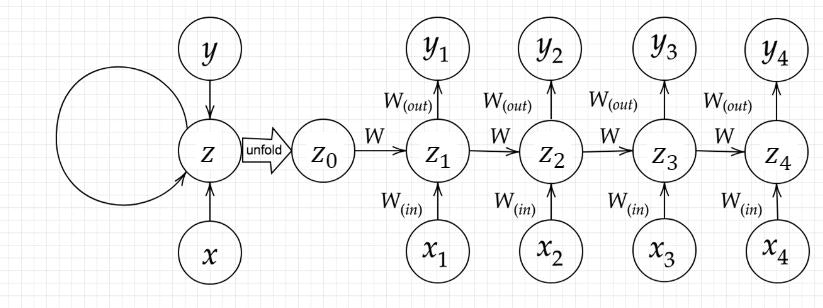
基本の考え方はこれまでと変わらないが、前の層からのWzt−1Wzt−1が増えていることが下記の式から分かる。
RNNの数学的記述
u^t=W_{(in)}x^t+Wz^{t−1}+b\\
z^t=f\left(W_{(in)}x^t+Wz^{t−1}+b \right)\\
v^t=W_{(out)}z^t+c\\
y^t=g\left(W_{(out)}z^t+c\right)
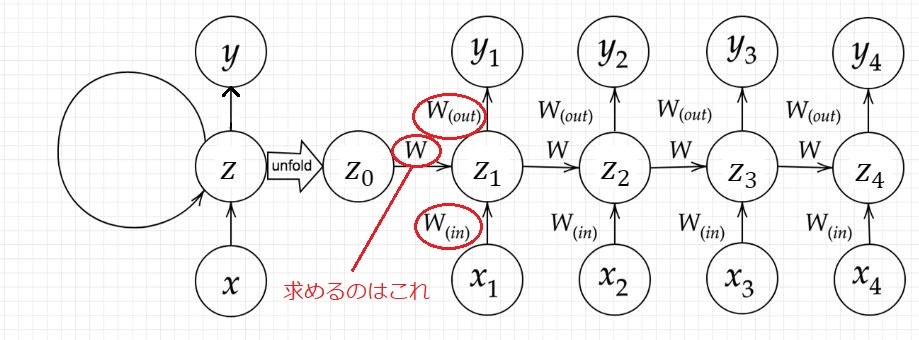
確認テスト:RNNのネットワークには大きく分けて3つの重みがある。
1つは入力から現在の中間層を定義する際にかけられる重み$W_{(in)}$、
1つは中間層から出力を定義する際に掛けられる重み$W_{(out)}$、
残り1つの重みについて説明せよ。
答:
求める1つの重みは、前の中間層から現在の中間層を定義する際にかけられる重み$W$、
これがRNNで一番大事。これがないとRNNではない。
このように、前の前のもの...と数珠つながりのものを再帰構造と言う。
RNNの正式名称は、Recurrent Neural Networkで、「Recurrent」が再帰。
特徴RNNの特徴とは?時系列モデルを扱うには、初期の状態と過去の時間$t-1$の状態を保持し、そこから次の時間でのtを再帰的に求める再帰構造が必要になる
実装
import numpy as np
from common import functions
import matplotlib.pyplot as plt
# def d_tanh(x):
# データを用意
# 2進数の桁数
binary_dim = 8
# 最大値 + 1
largest_number = pow(2, binary_dim)
# largest_numberまで2進数を用意
binary = np.unpackbits(np.array([range(largest_number)],dtype=np.uint8).T,axis=1)
input_layer_size = 2
hidden_layer_size = 16
output_layer_size = 1
weight_init_std = 1
learning_rate = 0.1
iters_num = 10000
plot_interval = 100
# ウェイト初期化 (バイアスは簡単のため省略)
W_in = weight_init_std * np.random.randn(input_layer_size, hidden_layer_size)
W_out = weight_init_std * np.random.randn(hidden_layer_size, output_layer_size)
W = weight_init_std * np.random.randn(hidden_layer_size, hidden_layer_size)
# Xavier
# He
# 勾配
W_in_grad = np.zeros_like(W_in)
W_out_grad = np.zeros_like(W_out)
W_grad = np.zeros_like(W)
u = np.zeros((hidden_layer_size, binary_dim + 1))
z = np.zeros((hidden_layer_size, binary_dim + 1))
y = np.zeros((output_layer_size, binary_dim))
delta_out = np.zeros((output_layer_size, binary_dim))
delta = np.zeros((hidden_layer_size, binary_dim + 1))
all_losses = []
for i in range(iters_num):
# A, B初期化 (a + b = d)
a_int = np.random.randint(largest_number/2)
a_bin = binary[a_int] # binary encoding
b_int = np.random.randint(largest_number/2)
b_bin = binary[b_int] # binary encoding
# 正解データ
d_int = a_int + b_int
d_bin = binary[d_int]
# 出力バイナリ
out_bin = np.zeros_like(d_bin)
# 時系列全体の誤差
all_loss = 0
# 時系列ループ←時間的なつながり
for t in range(binary_dim):
# 入力値
X = np.array([a_bin[ - t - 1], b_bin[ - t - 1]]).reshape(1, -1)
# 時刻tにおける正解データ
dd = np.array([d_bin[binary_dim - t - 1]])
u[:,t+1] = np.dot(X, W_in) + np.dot(z[:,t].reshape(1, -1), W)
z[:,t+1] = functions.sigmoid(u[:,t+1])
y[:,t] = functions.sigmoid(np.dot(z[:,t+1].reshape(1, -1), W_out))
#誤差
loss = functions.mean_squared_error(dd, y[:,t])
delta_out[:,t] = functions.d_mean_squared_error(dd, y[:,t]) * functions.d_sigmoid(y[:,t])
all_loss += loss
out_bin[binary_dim - t - 1] = np.round(y[:,t])
for t in range(binary_dim)[::-1]:
X = np.array([a_bin[-t-1],b_bin[-t-1]]).reshape(1, -1)
delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * functions.d_sigmoid(u[:,t+1])
# 勾配更新
W_out_grad += np.dot(z[:,t+1].reshape(-1,1), delta_out[:,t].reshape(-1,1))
W_grad += np.dot(z[:,t].reshape(-1,1), delta[:,t].reshape(1,-1))
W_in_grad += np.dot(X.T, delta[:,t].reshape(1,-1))
# 勾配適用
W_in -= learning_rate * W_in_grad
W_out -= learning_rate * W_out_grad
W -= learning_rate * W_grad
W_in_grad *= 0
W_out_grad *= 0
W_grad *= 0
if(i % plot_interval == 0):
all_losses.append(all_loss)
print("iters:" + str(i))
print("Loss:" + str(all_loss))
print("Pred:" + str(out_bin))
print("True:" + str(d_bin))
out_int = 0
for index,x in enumerate(reversed(out_bin)):
out_int += x * pow(2, index)
print(str(a_int) + " + " + str(b_int) + " = " + str(out_int))
print("------------")
lists = range(0, iters_num, plot_interval)
plt.plot(lists, all_losses, label="loss")
plt.show()
iters:0
Loss:1.880882000449014
Pred:[1 1 1 1 1 1 1 1]
True:[0 1 1 0 0 0 1 1]
89 + 10 = 255
iters:100
Loss:0.9179459561218519
Pred:[0 0 0 0 0 0 0 0]
True:[1 0 0 0 0 0 1 1]
32 + 99 = 0
iters:200
Loss:1.0965026306191943
Pred:[0 0 0 0 0 0 0 1]
True:[1 0 0 1 1 1 1 1]
96 + 63 = 1
iters:300
Loss:0.9844578468607753
Pred:[0 0 0 0 0 1 0 1]
True:[1 0 0 1 1 0 0 0]
78 + 74 = 5
iters:400
Loss:0.7575751666845291
Pred:[0 0 0 0 0 1 0 0]
True:[1 0 0 0 0 0 0 0]
103 + 25 = 4
iters:500
Loss:0.9899325418492222
Pred:[1 0 0 1 0 1 0 0]
True:[1 1 0 0 0 0 1 0]
102 + 92 = 148
iters:600
Loss:0.9744139886372228
Pred:[1 0 0 1 1 1 0 1]
True:[1 0 0 1 0 0 0 1]
74 + 71 = 157
iters:700
Loss:0.8601892579828597
Pred:[0 0 0 0 0 1 0 0]
True:[1 1 0 0 0 1 0 0]
115 + 81 = 4
iters:800
Loss:0.9704463498081195
Pred:[0 0 0 1 0 1 1 1]
True:[0 1 1 1 0 0 1 0]
46 + 68 = 23
iters:900
Loss:0.9184389404373193
Pred:[0 1 0 0 0 0 0 0]
True:[0 1 1 0 0 0 0 1]
54 + 43 = 64
iters:1000
Loss:0.9079700028329265
Pred:[1 0 0 0 0 1 0 0]
True:[1 0 0 1 0 1 1 0]
70 + 80 = 132
iters:1100
Loss:0.8648275278966141
Pred:[0 0 0 1 0 1 1 1]
True:[0 0 1 1 1 0 1 1]
45 + 14 = 23
iters:1200
Loss:1.0486213598781107
Pred:[0 1 1 1 1 1 0 1]
True:[1 0 0 0 0 0 0 1]
107 + 22 = 125
iters:1300
Loss:0.7456177507994118
Pred:[1 0 1 1 1 1 1 1]
True:[1 0 1 0 1 1 1 1]
86 + 89 = 191
iters:1400
Loss:1.0743843341286294
Pred:[1 1 1 0 1 1 0 1]
True:[1 0 0 1 0 0 0 1]
22 + 123 = 237
iters:1500
Loss:0.5386517637177797
Pred:[0 0 0 0 0 0 1 1]
True:[0 0 0 1 0 0 1 1]
17 + 2 = 3
iters:1600
Loss:0.962249738749221
Pred:[1 1 0 0 1 1 1 0]
True:[1 0 1 0 1 1 1 1]
48 + 127 = 206
iters:1700
Loss:0.9979620466402395
Pred:[1 0 1 0 0 0 0 0]
True:[1 0 1 0 1 1 0 0]
79 + 93 = 160
iters:1800
Loss:1.003557511553837
Pred:[1 0 0 0 0 0 0 0]
True:[1 0 1 1 1 1 0 0]
81 + 107 = 128
iters:1900
Loss:0.6553679926958368
Pred:[0 1 1 0 0 1 1 0]
True:[0 1 1 0 0 1 1 0]
92 + 10 = 102
iters:2000
Loss:0.7188275648093572
Pred:[0 1 1 0 1 0 0 0]
True:[0 1 1 0 1 1 0 0]
23 + 85 = 104
iters:2100
Loss:0.9539025563239608
Pred:[1 0 0 1 0 0 1 0]
True:[1 1 0 0 1 0 1 0]
108 + 94 = 146
iters:2200
Loss:0.4018997350257209
Pred:[0 0 1 1 0 0 0 1]
True:[0 0 1 1 0 0 0 1]
48 + 1 = 49
iters:2300
Loss:0.5644487880271725
Pred:[0 1 1 1 1 0 1 1]
True:[0 1 1 1 1 0 0 1]
53 + 68 = 123
iters:2400
Loss:0.647044199818138
Pred:[1 0 1 0 1 0 1 0]
True:[1 0 1 1 0 0 1 0]
84 + 94 = 170
iters:2500
Loss:0.5606520643631321
Pred:[1 0 0 0 1 1 0 0]
True:[1 0 1 0 1 1 0 0]
120 + 52 = 140
iters:2600
Loss:1.0174085823089247
Pred:[1 0 0 0 0 1 0 0]
True:[1 0 1 0 1 0 0 0]
127 + 41 = 132
iters:2700
Loss:0.7937846982899546
Pred:[1 0 0 0 0 0 1 1]
True:[1 0 1 0 0 0 0 1]
117 + 44 = 131
iters:2800
Loss:0.24726918337503054
Pred:[0 1 0 1 1 0 0 1]
True:[0 1 0 1 1 0 0 1]
87 + 2 = 89
iters:2900
Loss:0.69653255811168
Pred:[1 0 0 0 1 1 0 0]
True:[1 0 1 0 1 1 0 1]
56 + 117 = 140
iters:3000
Loss:0.250642136394793
Pred:[0 1 1 1 0 1 1 1]
True:[0 1 1 1 0 1 1 1]
43 + 76 = 119
iters:3100
Loss:0.4377399020863038
Pred:[1 0 1 0 0 1 1 1]
True:[1 0 0 0 0 1 1 1]
83 + 52 = 167
iters:3200
Loss:0.8071033561770065
Pred:[1 0 0 0 0 1 1 1]
True:[1 0 1 0 1 1 1 1]
123 + 52 = 135
iters:3300
Loss:0.12170468798372641
Pred:[1 0 0 0 1 1 0 0]
True:[1 0 0 0 1 1 0 0]
72 + 68 = 140
iters:3400
Loss:0.609934678127145
Pred:[1 0 0 0 0 0 1 1]
True:[1 1 0 0 0 0 1 1]
85 + 110 = 131
iters:3500
Loss:0.8533755449069229
Pred:[1 0 0 0 0 0 1 0]
True:[1 0 0 0 1 0 0 0]
125 + 11 = 130
iters:3600
Loss:0.4736081186043328
Pred:[0 0 1 1 1 0 0 0]
True:[0 0 1 1 1 0 1 0]
3 + 55 = 56
iters:3700
Loss:0.2505611468189348
Pred:[1 0 0 0 1 0 1 1]
True:[1 0 0 0 1 0 1 1]
118 + 21 = 139
iters:3800
Loss:0.15200380148120854
Pred:[0 1 0 1 1 0 1 0]
True:[0 1 0 1 1 0 1 0]
21 + 69 = 90
iters:3900
Loss:0.3843905235316184
Pred:[1 1 0 0 1 0 0 1]
True:[1 0 0 0 1 0 0 1]
57 + 80 = 201
iters:4000
Loss:0.500410736166812
Pred:[1 0 0 0 1 0 0 1]
True:[1 0 1 0 1 0 0 1]
121 + 48 = 137
iters:4100
Loss:2.432719111399627
Pred:[0 1 1 1 0 0 1 1]
True:[1 0 0 0 0 1 0 0]
121 + 11 = 115
iters:4200
Loss:0.09492870755259682
Pred:[0 0 0 1 1 1 0 1]
True:[0 0 0 1 1 1 0 1]
8 + 21 = 29
iters:4300
Loss:0.7466329570533933
Pred:[1 0 0 0 1 1 1 1]
True:[1 1 0 0 1 0 0 0]
113 + 87 = 143
iters:4400
Loss:0.8451692890571653
Pred:[0 1 0 0 0 0 0 0]
True:[0 1 0 1 1 0 1 0]
31 + 59 = 64
iters:4500
Loss:1.7506820618177794
Pred:[0 1 1 0 1 1 1 0]
True:[0 1 1 1 0 0 0 0]
34 + 78 = 110
iters:4600
Loss:0.07786234824649915
Pred:[0 1 1 0 0 1 1 1]
True:[0 1 1 0 0 1 1 1]
27 + 76 = 103
iters:4700
Loss:0.3362267241982123
Pred:[1 0 0 0 0 0 1 0]
True:[1 0 0 0 1 0 1 0]
30 + 108 = 130
iters:4800
Loss:0.31985358710133216
Pred:[0 1 0 1 0 1 0 0]
True:[0 1 0 1 0 1 1 0]
83 + 3 = 84
iters:4900
Loss:0.07352044799726921
Pred:[1 0 0 0 0 1 1 0]
True:[1 0 0 0 0 1 1 0]
34 + 100 = 134
iters:5000
Loss:0.2241604076393991
Pred:[0 1 0 1 0 1 0 1]
True:[0 1 0 1 0 1 0 0]
41 + 43 = 85
iters:5100
Loss:0.4761439669474385
Pred:[1 0 0 0 0 0 0 1]
True:[1 0 0 1 0 1 0 1]
119 + 30 = 129
iters:5200
Loss:0.012644357534140739
Pred:[0 1 1 1 0 1 0 0]
True:[0 1 1 1 0 1 0 0]
12 + 104 = 116
iters:5300
Loss:0.349483918299702
Pred:[1 0 1 0 0 0 0 0]
True:[1 0 1 0 0 0 0 0]
125 + 35 = 160
iters:5400
Loss:0.10073319208308
Pred:[0 1 1 1 1 0 1 1]
True:[0 1 1 1 1 0 1 1]
33 + 90 = 123
iters:5500
Loss:0.10126713680619047
Pred:[0 1 1 1 1 1 0 0]
True:[0 1 1 1 1 1 0 0]
121 + 3 = 124
iters:5600
Loss:0.14471654750370752
Pred:[1 0 0 0 0 0 0 0]
True:[1 0 0 0 0 0 0 0]
77 + 51 = 128
iters:5700
Loss:0.10221272021127785
Pred:[0 1 0 0 0 0 1 1]
True:[0 1 0 0 0 0 1 1]
63 + 4 = 67
iters:5800
Loss:0.016597011507277833
Pred:[1 0 0 1 1 0 0 0]
True:[1 0 0 1 1 0 0 0]
112 + 40 = 152
iters:5900
Loss:0.03340415721504745
Pred:[1 0 0 1 0 1 1 0]
True:[1 0 0 1 0 1 1 0]
40 + 110 = 150
iters:6000
Loss:0.010583662185066003
Pred:[1 0 1 0 0 1 1 0]
True:[1 0 1 0 0 1 1 0]
68 + 98 = 166
iters:6100
Loss:0.23280717643482976
Pred:[1 0 1 0 0 0 0 0]
True:[1 0 1 0 0 0 0 0]
51 + 109 = 160
iters:6200
Loss:0.04648384233865519
Pred:[1 0 1 0 1 0 1 0]
True:[1 0 1 0 1 0 1 0]
54 + 116 = 170
iters:6300
Loss:0.006462744445722863
Pred:[0 0 1 1 0 0 1 0]
True:[0 0 1 1 0 0 1 0]
40 + 10 = 50
iters:6400
Loss:0.10109790159812973
Pred:[1 0 0 1 0 1 0 1]
True:[1 0 0 1 0 1 0 1]
102 + 47 = 149
iters:6500
Loss:0.0429515029496157
Pred:[1 0 0 1 0 0 1 1]
True:[1 0 0 1 0 0 1 1]
101 + 46 = 147
iters:6600
Loss:0.004182186925407523
Pred:[0 1 0 1 1 1 1 0]
True:[0 1 0 1 1 1 1 0]
50 + 44 = 94
iters:6700
Loss:0.04824084602627439
Pred:[0 1 1 1 0 1 1 1]
True:[0 1 1 1 0 1 1 1]
91 + 28 = 119
iters:6800
Loss:0.05815328931730915
Pred:[1 1 0 0 1 0 1 1]
True:[1 1 0 0 1 0 1 1]
87 + 116 = 203
iters:6900
Loss:0.015508494679495218
Pred:[1 0 0 0 1 1 0 1]
True:[1 0 0 0 1 1 0 1]
44 + 97 = 141
iters:7000
Loss:0.028835911989802142
Pred:[1 0 1 0 0 0 1 1]
True:[1 0 1 0 0 0 1 1]
77 + 86 = 163
iters:7100
Loss:0.0065328152429834
Pred:[0 1 1 0 0 1 0 0]
True:[0 1 1 0 0 1 0 0]
72 + 28 = 100
iters:7200
Loss:0.0263647736234224
Pred:[0 1 0 1 1 0 0 1]
True:[0 1 0 1 1 0 0 1]
86 + 3 = 89
iters:7300
Loss:0.009269665901022605
Pred:[0 1 0 1 1 1 0 1]
True:[0 1 0 1 1 1 0 1]
72 + 21 = 93
iters:7400
Loss:0.0663000089290625
Pred:[1 0 0 0 1 1 0 1]
True:[1 0 0 0 1 1 0 1]
31 + 110 = 141
iters:7500
Loss:0.0382769830900471
Pred:[0 1 1 0 1 1 0 1]
True:[0 1 1 0 1 1 0 1]
50 + 59 = 109
iters:7600
Loss:0.03410697088323891
Pred:[0 1 1 0 1 1 0 0]
True:[0 1 1 0 1 1 0 0]
101 + 7 = 108
iters:7700
Loss:0.007293635641616147
Pred:[0 1 1 1 1 1 0 1]
True:[0 1 1 1 1 1 0 1]
16 + 109 = 125
iters:7800
Loss:0.005691477257042054
Pred:[0 1 1 1 0 0 1 1]
True:[0 1 1 1 0 0 1 1]
76 + 39 = 115
iters:7900
Loss:0.004038425412700082
Pred:[0 1 1 1 1 0 1 0]
True:[0 1 1 1 1 0 1 0]
104 + 18 = 122
iters:8000
Loss:0.006741143585235675
Pred:[0 1 0 0 1 1 0 1]
True:[0 1 0 0 1 1 0 1]
56 + 21 = 77
iters:8100
Loss:0.022208309842287808
Pred:[1 0 1 1 0 1 1 1]
True:[1 0 1 1 0 1 1 1]
59 + 124 = 183
iters:8200
Loss:0.016476340750261376
Pred:[0 1 1 1 0 0 0 0]
True:[0 1 1 1 0 0 0 0]
43 + 69 = 112
iters:8300
Loss:0.0033983326619467127
Pred:[0 1 1 1 1 1 1 0]
True:[0 1 1 1 1 1 1 0]
120 + 6 = 126
iters:8400
Loss:0.002033625830187354
Pred:[0 1 0 1 0 1 1 0]
True:[0 1 0 1 0 1 1 0]
70 + 16 = 86
iters:8500
Loss:0.01222149836495782
Pred:[0 1 1 0 0 0 0 0]
True:[0 1 1 0 0 0 0 0]
26 + 70 = 96
iters:8600
Loss:0.006205040005362372
Pred:[0 1 0 0 1 1 1 1]
True:[0 1 0 0 1 1 1 1]
67 + 12 = 79
iters:8700
Loss:0.005285430492698029
Pred:[0 0 1 1 1 1 1 0]
True:[0 0 1 1 1 1 1 0]
9 + 53 = 62
iters:8800
Loss:0.014395636336412363
Pred:[0 1 0 1 0 0 0 1]
True:[0 1 0 1 0 0 0 1]
3 + 78 = 81
iters:8900
Loss:0.0027323916060502124
Pred:[0 1 1 1 1 1 0 1]
True:[0 1 1 1 1 1 0 1]
116 + 9 = 125
iters:9000
Loss:0.006617991871368012
Pred:[1 0 0 1 0 0 1 1]
True:[1 0 0 1 0 0 1 1]
115 + 32 = 147
iters:9100
Loss:0.00376737574781922
Pred:[0 1 1 0 0 0 1 1]
True:[0 1 1 0 0 0 1 1]
26 + 73 = 99
iters:9200
Loss:0.00313782205668562
Pred:[0 0 1 0 0 1 1 1]
True:[0 0 1 0 0 1 1 1]
6 + 33 = 39
iters:9300
Loss:0.004458775642844024
Pred:[0 0 1 0 0 1 1 0]
True:[0 0 1 0 0 1 1 0]
9 + 29 = 38
iters:9400
Loss:0.006498236031182415
Pred:[0 1 1 0 1 0 1 0]
True:[0 1 1 0 1 0 1 0]
53 + 53 = 106
iters:9500
Loss:0.015262103181597838
Pred:[0 1 1 1 1 0 0 1]
True:[0 1 1 1 1 0 0 1]
27 + 94 = 121
iters:9600
Loss:0.012604253152994425
Pred:[1 1 1 0 0 1 0 1]
True:[1 1 1 0 0 1 0 1]
114 + 115 = 229
iters:9700
Loss:0.0019401503419889093
Pred:[1 0 1 0 0 0 0 0]
True:[1 0 1 0 0 0 0 0]
92 + 68 = 160
iters:9800
Loss:0.01015307506660753
Pred:[0 0 0 1 1 0 0 0]
True:[0 0 0 1 1 0 0 0]
10 + 14 = 24
iters:9900
Loss:0.003820552982528546
Pred:[1 0 1 1 1 1 1 1]
True:[1 0 1 1 1 1 1 1]
83 + 108 = 191
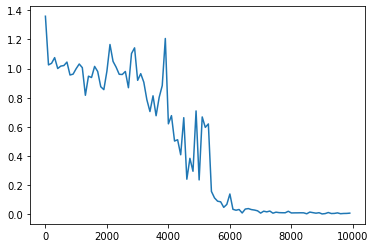
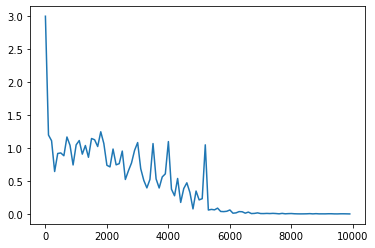
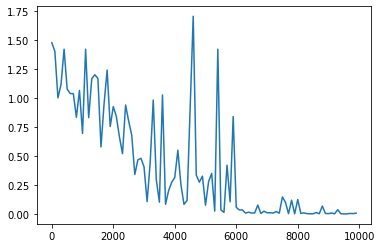
weight_init_std = 1、learning_rate = 0.1、hidden_layer_size = 16
weight_init_std = 1、learning_rate = 0.1、hidden_layer_size = 4
weight_init_std = 1、learning_rate = 0.1、hidden_layer_size = 8
weight_init_std = 1、learning_rate = 0.1、hidden_layer_size = 32
weight_init_std = 1、learning_rate = 0.1、hidden_layer_size = 64
・構文木(こうぶんぎ)
昨日/私/は/ラーメン/を/食べ/ました。
⇒単語間の特徴量を取っていくと最終的には1つの特徴量(木構造)になる。
⇒単語間のつながりは何らかの数字の集まり(特徴量)で表される。
⇒その数字の集まりが保たれた状態。
第2章 BPTT
2.1 BPTTとは
RNNにおける誤差逆伝播法の1つで時系列の考え方を取り入れたもの。
⇒ 誤差逆伝播の一種
2.1 誤差逆伝播法の復習
\begin{eqnarray}
E(\mathbb{y})&=&\frac12\sum_{j=1}^{l}\left(y_j-d_j \right)^2=\frac12\|\mathbb{y}-\mathbb{d}\|^2\\
\mathbb{y}&=&\mathbb{u}^{(l)}\\
\mathbb{u}^{(l)}&=&\mathbb{w}^{(l)}\mathbb{z}^{(l-1)}+\mathbb{b}^{(l)}\\
\frac{\partial E}{\partial w_{ji}^{(2)}}&=&\frac{\partial E}{\partial \mathbb{y}}\times \frac{\partial \mathbb{y}}{\partial \mathbb{u}}\times \frac{\partial \mathbb{u}}{\partial w_{ji}^{(2)}}\\
\frac{\partial E(\mathbb{y})}{\partial \mathbb{y}}&=&\frac{\partial }{\partial \mathbb{y}}\frac12\|\mathbb{y}-\mathbb{d}\|^2=\mathbb{y}-\mathbb{d}\\
\frac{\partial \mathbb{y(\mathbb{u})}}{\partial \mathbb{u}}&=&\frac{\partial \mathbb{u}}{\partial \mathbb{u}}=1
\end{eqnarray}
計算結果(=誤差)から微分を逆算することで、不要な再帰的計算を避けて微分を算出できる。
確認テスト:連鎖率を使い、$\displaystyle\frac{dz}{dx}$を求めよ。
\left\{
\begin{array}{l}
z=t^2 \\
t=x+y
\end{array}
\right.
答:微分の連鎖率は
$$\frac{dz}{dx}=\frac{dz}{dt}\times\frac{dt}{dx}$$
\left\{
\begin{array}{l}
\frac{dz}{dt}=2t \\
\frac{dt}{dx}=1
\end{array}
\right.
より
$$\frac{dz}{dx}=\frac{dz}{dt}\times\frac{dt}{dx}=2t\times 1=2(x+y)$$
2.2 BPTTの数学的記述1
\frac{\partial E}{\partial W_{(in)}}=\frac{\partial E}{\partial u^t}\left[\frac{\partial u^t}{\partial W_{(in)}}\right]^T=\delta^t[x^t]^T
np.dot(X.T, delta[:,t].reshape(1,-1))
\frac{\partial E}{\partial W_{(out)}}=\frac{\partial E}{\partial v^t}\left[\frac{\partial v^t}{\partial W_{(out)}}\right]^T=\delta^{out,t}[z^t]^T
np.dot(z[:,t+1].reshape(-1,1), delta_out[:,t].reshape(-1,1))
\frac{\partial E}{\partial W}=\frac{\partial E}{\partial u^t}\left[\frac{\partial u^t}{\partial W}\right]^T=\delta^t[z^{t-1}]^T
np.dot(z[:,t].reshape(-1,1), delta[:,t].reshape(1,-1))
2.3 BPTTの数学的記述2
u^t=W_{(in)}x^t+Wz^{t−1}+b\\
z^t=f\left(W_{(in)}x^t+Wz^{t−1}+b \right)\\
v^t=W_{(out)}z^t+c\\
y^t=g\left(W_{(out)}z^t+c\right)
確認テスト:下図の$y_1$を$x_1,s_0,s_1,w_{in},w,w_{out}$を用いて数式で表わせ。
また、中間層の出力にシグモイド関数を作用させよ。
答:
z_1=sigmoid \left( s_0 W+x_1W_{in}+b \right)\\
y_1=sigmoid \left( z_1 W_{out}+c \right)
2.4 BPTTの数学的記述3
$b$:中間層のバイアス、$c$:出力層のバイアス
W^{t+1}_{(in)}=W^{t}_{(in)}-\epsilon\frac{\partial E}{\partial W_{(in)}}=W^t_{(in)}-\epsilon\sum_{z=0}^{T_t}\delta^{t-z}[x^{t-z}]^T\\
W^{t+1}_{(out)}=W^{t}_{(out)}-\epsilon\frac{\partial E}{\partial W_{(in)}}=W^t_{(out)}-\epsilon\delta^{out,t}[z^{t}]^T\\
W^{t+1}=W^{t}-\epsilon\frac{\partial E}{\partial W}=W^t_{(in)}-\epsilon\sum_{z=0}^{T_t}\delta^{t-z}[z^{t-z-1}]^T\\
b^{t+1}=b^t−\epsilon \frac{\partial E}{\partial b}=b^t−\epsilon \sum_{z=0}^{T_t} \sigma^{t−z}\\
c^{t+1}=c^t−\epsilon\frac{\partial E}{\partial c} =c^t−\epsilon \delta^{out,t}
第3章LSTM(Long Short Term Memory)
RNNの課題
⇒ 時系列を遡れば遡るほど勾配が消失する。
⇒ 長い時系列の学習が困難
勾配消失の解決(活性化関数や重み等の初期化の手法を変える)方法もあるが、
他に構造自体を変えて解決したものがLSTM(Long Short Term Memory)
LSTMそうではゲートと呼ばれる仕組みを導入
過去の情報を忘れるか・忘れないかを判断しながら、必要な情報だけ次の時刻に引き継ぐことができる。
LSTMは、RNN(Recurrent Neural Network)の拡張として1995年に登場
由来は長期記憶(Long term memory)と短期記憶(Short term memory)という用語から
勾配消失問題の復習
誤差逆伝播法が下位層に進んでいくに連れて、勾配がどんどん緩やかになっていく。
そのため、勾配降下法による、更新では下位層のパラメータはほとんど変わらず、訓練は最適値に収束しなくなる。
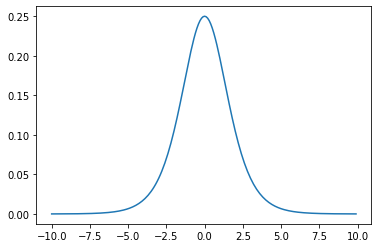
確認テスト:シグモイド関数を微分した時、入力値が0の時に最大の値を取る。
その値はいくつか。
答:シグモイド関数の微分は、
$$f′(x)=(1−f(x))\times f(x)$$
となる。シグモイド関数$f(x)=sigmoid(x)$ に入力値$x=0$を代入すると
f(x)=\frac{1}{1+e^{−x}}\\
f(0)=\frac{1}{1+e^{0}}=\frac12=0.5
となるので、$f′(x)=(1−f(x))\times f(x)$ に $x=0$ を代入すると
$$f′(0)=(1−f(0))\times f(0)=(1−0.5)\cdot 0.5=0.25$$
3.1 CEC(Constant Error Carousel)
過去のデータを保存するためのユニット。
CEC単独では以下のような問題があるためゲート、覗き穴結合で解決する。
CECの課題
⇒入力データについて、時間依存度に関係なく重みが一律である。
⇒ニューラルネットワークの学習特性が無いということ。
過去の情報をすべて持っているため、その情報がいらなくなってもずっと影響を及ぼしてしまう問題
CEC自身の値はゲートの制御に影響を与えないためCECの過去の情報を任意のタイミングで伝搬させたり忘却させたり出来ない問題。
3.2 入力・出力ゲート
入力・出力ゲートを追加することで、それぞれのゲートへの入力値の重みを、重み行列$W$ , $U$で可変可能とすることで、CECの課題を解決。
入力ゲート:1つ前の時刻の出力をどの程度反映するか調整する。
$$i=\sigma(W_ih_{t−1}+U_ix_t)$$
出力ゲート:過去の出力を入力にフィードバックする。
$$o=\sigma(W_oh_{t−1}+U_ox_t)$$
3.3 忘却ゲート
CECの中身をどの程度残すか(いらない情報を忘却する)を調整する。
$$f=\sigma(W_fh_{t−1}+U_fx_t)$$
確認テスト:以下の文章をLSTMに入力し、空欄に当てはまる単語を予測したいとする。
文中の「とても」という言葉は空欄の予測においてなくなっても影響を及ぼさないと考えられる。
このような場合、どのゲートが作用すると考えられるか。
「映画おもしろかったね。ところで、とてもお腹が空いたから何か____。」
答:忘却ゲート
3.4 メモリセル
g=\tan h\left(W_gh_{t−1}+U_gx_t \right)\\
c_t=(c_{t−1} \otimes f)\oplus(g\otimes i)
3.5 出力
$$h_t=\tan h(c_t)\otimes o$$
3.6 覗き穴結合
CEC自身の値に、重み行列を介して伝搬可能にした構造。
3.7 GRU(Gated Recurrent Unit)
LSTMでは、パラメータ数が多く、計算負荷が高くなる問題があった ⇒ GRU
GRU(Gated Recurrent Unit)とは?
GRUは、LSTMを改良したもの。
従来のLSTMでは、パラメータが多数存在していたため、計算負荷が大きかった。
しかし、GRUでは、そのパラメータを大幅に削減し、精度は同等またはそれ以上が望める様になった構造
入力ゲートと忘却ゲートが統合され更新ゲート(Update gate)になっている。
記憶セルと出力ゲートがなく、値を0にリセットするリセットゲートがある。
メリットは、計算負荷が低い。
確認テスト:LSTMとCECが抱える課題について、それぞれ簡潔に述べよ。
答:LSTM:パラメータ数が多く、計算負荷が高い
CEC:ニューラルネットワークの学習特性がない
確認テスト:LSTMとGRUの違いを簡潔に述べよ。
LSTMでは、パラメータが多数存在していたため、計算負荷が大きかった。
GRUでは、パラメータを大幅に削減し、精度は同等またはそれ以上が望める様になった構造で、計算負荷が低い。
第4章 双方向RNN(Bindirectional RNN)
第4章 双方向RNN
通常のRNNは過去の情報を保持することで時系列データの学習モデル
双方向RNNは過去の情報に加えて「未来の情報も加味」することで制度を向上させるためのモデル
第5章RNNでの自然言語処理 Seq2Seq(Sequence to Sequence)
Seq2Seqは、Sequence(系列)を受け取り、別のSequence(系列)に変換するモデル。
自然言語処理でよく用いられる。
RNNをベースにした文章などの入力を圧縮する(Encoder)と、出力を展開する(Decoder)からなるモデル(Encoder-Decoderモデルの一種)
機械翻訳、文章要約、対話(自分の発言⇒相手の発言、チャットボット)などに用いられる。
Seq2Seqの具体的な用途
⇒ 機械対話や機械翻訳等に使用されている。
例えば機械翻訳の場合、Encoderに日本語を入力し、Decoderの出力で英語を得る等といった形となる。
一問一答しかできないという課題がある。
文脈もなくただ応答するというイメージ。
5.1 Encoder RNN
Taking:文章を単語等のトークンごとに分割し、さらにトークンごとのIDに分割する。
Embedding:IDからそのトークンを表す分散表現ベクトルに変換する。
Encoder RNN:ベクトルを順にRNNに入力していく。
5.2 Encoder RNN処理手順
単語分散表現ベクトル1を入力して隠れ層の値を得る。
↓
次の単語分散表現ベクトル2と単語分散表現ベクトル1の隠れ層の値を入力して隠れ層の値を得る。
↓
上記を繰り返して最後の単語分散表現ベクトルと前までの隠れ層の値から得た隠れ層の値をFinal state(Thought vector)とする。
Thought vectorは入力した分の意味を表すベクトルであり、これがDecoderへの入力となる。
5.3 Decoder RNN
システムがアウトプットデータを、単語等のトークンごとに生成する構造。
5.4 Decoder RNNの処理の流れ
Encoder RNNのfinal state(thought vector)から各トークンの生成確率を出力していく。
↓
生成確率に基づいてトークンをランダムに選ぶ。
↓
選ばれたトークンの単語分散表現ベクトルを次の入力とする。
↓
上記を繰り返して得られたトークンを文字列に戻すことで文章を生成する。
DecoderはEncoderの逆のことをしているイメージ。
確認テスト:下記の選択肢から、seq2seqについて説明しているものを選べ。
(1)時刻に関して順方向と逆方向のRNNを構成し、それら2つの中間層表現を特徴量として利用するものである。
(2)RNNを用いたEncoder-Decoderモデルの一種であり、機械翻訳などのモデルに使われる。
(3)構文木などの木構造に対して、隣接単語から表現ベクトル(フレーズ)を作るという演算を再帰的に行い(重みは共通)、文全体の表現ベクトルを得るニューラルネットワークである。
(4)RNNの一種であり、単純なRNNにおいて問題となる勾配消失問題をCECとゲートの概念を導入することで解決したものである。
答:(2)seq2seqはRNNを用いたEncoder-Decoderモデルの一種であり、機械翻訳などのモデルに使われる。
(1)は「双方向RNN」
(3)は「Recursive Neural Network」
(4)は「LSTM」
Seq2seqの課題
⇒ 一問一答しかできない
⇒ 問に対して文脈も何もなく、ただ応答が行われる続ける
⇒ そこで、HRED(A Hierarchical Recurrent Encoder-Decoder)
5.5 HRED(エイチレッド:A Hierarchical Recurrent Encoder-Decoder)
過去$n−1$の発話から次の発話を生成する。
前の単語の流れに即して応答されるため、Seq2Seqより人間らしい文章が生成される。
参考:Seq2seqでは、会話の文脈無視で応答がなされた。
5.6 HREDの構造
HRED=Seq2Seq + Context RNN
Context RNN: Encoder のまとめた各文章の系列をまとめて、これまでの会話コンテキスト全体を表すベクトルに変換する構造。
⇒ 過去の発話の履歴を加味した返答をできる。
HRED は確率的な多様性が字面にしかなく、会話の「流れ」のような多様性が無い。
⇒ 同じコンテキスト(発話リスト)を与えられても、答えの内容が毎回会話の流れとしては同じものしか出せない。
HRED は短く情報量に乏しい答えをしがちである。
⇒ 短いよくある答えを学ぶ傾向がある。
⇒ やる気のないLINEの返答のような解答
「うん」「そうだね」「・・・」など。
5.7 VHRED(Latent Variable Hierarchical Recurrent Encoder-Decoder)
HREDにVAEの洗潜在変数の概念を追加したもの。
⇒ HREDの課題を、VAEの潜在変数の概念を追加することで解決した構造。
確認テスト:Seq2SeqとHRED、HREDとVHREDの違いを簡潔に述べよ。
答:Seq2SeqとHRED:Seq2Seqは一問一答しかできないが、HREDは$n−1$の発話から文脈に応じた回答ができる。
HREDとVHRED:HREDは発話に多様性がなく情報量に乏しいが、VHREDはそれらの課題を解決し、多様性ある発話ができる。
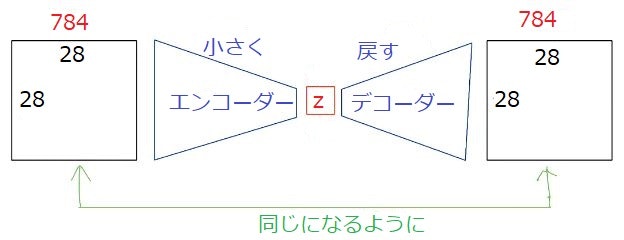
5.8 オートエンコーダ(Auto Encoder)
教師なし学習の1つ。
教師なし学習:人間がラベル付けしたデータを使わずに入力と出力を行うモデル。
初めは画像で使われた
⇒ MNIST(0~9の数字を予測するモデル)
自己符号化器とも呼ぶ。
例えば入力した画像と同じ画像を出力する。
可視層と隠れ層の2層のネットワークであり、入力および出力が可視層のため、隠れ層で次元削減し元データを復元するため、データを圧縮することができる。
可視層⇒隠れ層⇒可視層の順で学習する。これを順に実施することにより多層へ応用しても学習の収束が可能になった。
Encoder:入力データから潜在変数$z$に変換するニューラルネットワーク
Decoder:潜在変数$z$から元画像を復元するニューラルネットワーク
出力した画像の潜在変数zzが入力画像より小さくなっていれば次元削減とみなすことができる。
その他、ノイズ除去や異常検知にも使われる。
5.8 VAE(変分オートエンコーダ:Variational Autoencoder)
通常のオートエンコーダの場合、潜在変数$z$の中身はブラックボックスになっている。VAE(変分オートエンコーダ)は、潜在変数を調整することで出力の特徴を調整することができます。
VAEは確率分布を利用することで連続的に変化する画像を生成することができます。
VAEは潜在変数$z$に確率分布$z$~$N(0,1)$を仮定したもの。
生成モデル:訓練データを学習し、それらのデータと似たような新しいデータを生成するモデルのこと。
⇒訓練データの分布と生成データの分布が一致するように学習する。
識別モデルは、所属確率を求めることで入力をグループ分けする。
生成モデルは、確率分布を推定することでデータそのものを作ることができる。
代表的なものはVAE、GAN
確認テスト:VAEに関する下記の説明文中の空欄にて当てはまる言葉を答えよ。
自己符号化器の潜在変数に_____を導入したもの。
答:確率分布
第6章 Word2vec
単語をベクトル化し、次元を圧縮する。
課題:RNNでは、単語のような可変長の文字列をNNに与えることはできない。
⇒ 固定長形式で単語を表す必要がある。
自然言語処理の流れ
Word2vecで小さなベクトル表現に単語を置き換えたものをNN(seq2seq)
に放り込んで、自分がやりたいことをやる。
メリット
⇒大規模データの分散表現の学習が、現実的な計算速度とメモリ量で実現可能にした
×:ボキャブラリ×ボキャブラリだけの重み行列が誕生。
○:ボキャブラリ×任意の単語ベクトル次元で重み行列が誕生。
6.1 one-hot ベクトル
私は刺身を食べた
| 私 | は | 刺身 | を | 食べた | |
|---|---|---|---|---|---|
| ID | 0 | 1 | 2 | 3 | 4 |
「私」のone-hotベクトル:[1 0 0 0 0]
「は」のone-hotベクトル:[0 1 0 0 0]
「刺身」のone-hotベクトル:[0 0 1 0 0]
「を」のone-hotベクトル:[0 0 0 1 0]
「食べた」のone-hotベクトル:[0 0 0 1 0]
6.2 単語分散表現
one-hotベクトルと違い、単語を低次元の実数値ベクトルで表すこと。
単語同士の計算ができる。
one-hotベクトルでは単語間の関連性を得られないため分散表現にする必要がある。
単語分散表現ベクトルとすることで単語の意味に基づいたような計算もできるようになる。
King - Man + Woman = Queen
王-男+女=女王
6.3 Word2vec
Word2vecは分散表現を作成することができるツール
分散表現では、CBOW(Continuous Bag-of-Words)もしくはSkip-gramというNNが用いられる。
CBOW:前後の単語から対象の単語を予測するNNで、学習に要する時間がSkip-gramより短くなる。
Skip-gram:ある単語から、前後の単語を予測するNN。CBOWよりも学習時間がかかるが、制度が良い。
第7章 AttentionMechanism
Attentionは、時系列データの特定部分に注意を向けて学習させていく方法
Encoderの各時刻に、Decoderに渡す。
Decoderの各時刻に、Encoderから渡された出力のうち注意すべきベクトルを選んで合流させる。
Attention
⇒ 文章中のどの単語に注目すればよいのかを表すスコア
⇒ Query、key、Valueの3つのベクトルで計算される。
Query:Inputのうち検索をかけたいもの。
Key:検索対象とQueryの近さを測る
Value:keyにもとづき適切なValueを出力する。
seq2seq の問題は長い文章への対応が難しい
⇒ seq2seq では、中間層・隠れ層の大きさは決まっている。
⇒ 2単語でも、100単語でも、固定次元ベクトルの中に入力しなければならない。
解決策:文章が長くなるほどそのシーケンスの内部表現の次元も大きくなっていく(歯抜けになってしまう)、仕組みが必要
入力
私はペンを持っている
私\は\ペン\を\持って\いる
出力
I have a pen.
「a」については、そもそも関連度が低く、(重要ではない)
「I」については「私」との関連度が高い。
このようにすることで、途中の中間層・隠れ層の情報が一定でも、重要な情報だけを拾い集めて、その中で使っていくことができる。
近年、特に性能が上がっている自然言語のメカニズムは全部AttentionMechanism
確認テスト:RNNとWord2vec、Seq2Seq、Seq2Seq+Attentionの違いを簡潔に述べよ。
答:
RNNとWord2vec:
RNN:時系列データを処理するのに適したNN
Word2vec:単語の分散表現ベクトルを得る手法
Seq2SeqとAttention:
Seq2Seq:一つの時系列データから別の時系列データを得るネットワーク
時系列の中身に対して、関連性に重みをつける手法。