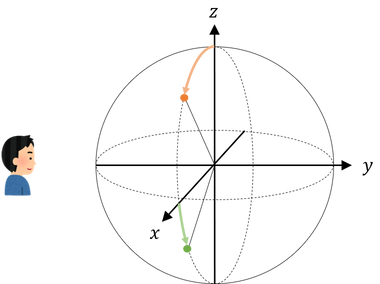Quantum Katas で始める量子コンピュータ入門 |3⟩: Measuerment

前書き

本記事では、Quantum Katas の Mesurement について解説します。Q# や Quantum Katas って何よという方は Quantum Katas で始める量子コンピュータ入門 |0⟩ をご参照ください。

また、既に BasicGates や SuporePosition を実施された方はなんとなくブロッホ球上の量子ビットが想像でき始めていて、ちょっと気を抜くと壊れてしまう量子ビットに対する愛着が芽生え始めているのではと思いますが、この Kata では片っ端から観測し、量子ビットを壊します。ただ、何も考えずに観測してしまうと結果は確率的にしか得ることができず、意味のある結果が得られないため、想定される状態を踏まえた上で量子ビットを操作して観測を行います。この操作にこれまでの BasicGates 等の知識が必要となります。

それでは早速進めていきましょう。

各 Task の解説

Task 1.1. |0⟩ or |1⟩ ?

問題

入力: $|1⟩$ もしくは $|0⟩$ であることが保証された 1 量子ビット

出力: 量子ビットが $|1⟩$ なら True を、$|0⟩$ なら False を返す。

解説

まずは初めての観測です。この問題は入力が $|1⟩$ もしくは $|0⟩$ であることが保証されているため、単純に観測した結果に基づいて条件分岐をすれば回答になります。

operation IsQubitOne (q : Qubit) : Bool
{
    body
    {
        if(M(q) == One) {
            return true;
        }
        else{
            return false;
        }
    }
}

観測をした結果は Result 型で、One もしくは Zero という値をとるという点に注意してください。

Task 1.2. |+⟩ or |-⟩ ?

問題

入力: $|+⟩ = \frac{|0⟩ + |1⟩}{\sqrt 2}$ もしくは $|-⟩= \frac{|0⟩ + |1⟩}{\sqrt 2}$ であることが保証された 1 量子ビット

出力: 量子ビットが $|+⟩$ なら True を、$|-⟩$ なら False を返す。

解説

先ほどの問題は単純に観測すればよさそうですが、今回入力として与えられる $|+⟩$ と $|-⟩$ はどちらも確率 0.5 で $|0⟩$ をとるため、そのまま観測すると区別がつきません。とはいえそんなに難しく考える必要はなく、アダマール ゲートを使えば $|+⟩$ は $|0⟩$に、$|-⟩$ は $|1⟩$になるため、アダマール処理後に観測すれば区別できそうです。回答は以下となります。

operation IsQubitPlus (q : Qubit) : Bool
{
    body
    {
        H(q);
        if(M(q) == Zero) {
            return true;
        }
        else{
            return false;
        }
    }
}

Task 1.3. |A⟩ or |B⟩ ?

問題

入力: Double 型の角度 $\alpha$、および以下の$|A⟩$ または $|B⟩$ であることが保証された量子ビット
$$ |A⟩ = \cos \alpha |0⟩ + \sin \alpha |1⟩ $$
$$ |B⟩ = -\sin \alpha |0⟩ + \cos \alpha |1⟩ $$

出力: 量子ビットが $|A⟩$ なら True を、$|B⟩$ なら False を返す。

回答

これもどこかで見たことのある問題ですね。BasicGates でも SuperPosition でも出てきましたが、$R_y$ ゲートを使えば上記の状態が作れるのでした。それぞれの Kata では角度 $\alpha$ だけ変化させて上記の状況を作ったので、逆に $-\alpha$ だけ変化させれば元の $|0⟩$ と $|1⟩$ を作成できそうです。回答は以下となります。

operation IsQubitA (alpha : Double, q : Qubit) : Bool
{
    body
    {
        Ry(-2.0 * alpha, q);
        // ...
        if(M(q) == Zero) {
            return true;
        }
        else{
            return false;
        }
    }
}

Task 1.4. |00⟩ or |11⟩ ?

問題

入力: $|00⟩$ または $|11⟩$ であることが保証された 2 量子ビット

出力: 量子ビットが $|00⟩$ なら 0 を、$|11⟩$ なら 1 を返す。

解説

2 量子ビットになりましたが、やることは最初と変わりません。

operation ZeroZeroOrOneOne (qs : Qubit[]) : Int
{
    body
    {
        if(M(qs[0]) == Zero) {
            return 0;
        }
        else{
            return 1;
        }
    }
}

Task 1.5. Distinguish four basis states

問題

入力: $|00⟩$, $|01⟩$, $|10⟩$, または $|11⟩$ であることが保証された 2 量子ビット

出力: $|00⟩$ なら 0、 $|01⟩$ なら 1, $|10⟩$ なら 2, $|11⟩$ なら 3 を返す。

解説

この問題もやることは最初と変わりません。それぞれの量子ビットを観測して、結果を返せばよさそうです。

operation BasisStateMeasurement (qs : Qubit[]) : Int
{
    body
    {
        if(M(qs[0]) == Zero && M(qs[1]) == Zero) {
            return 0;
        }
        elif(M(qs[0]) == Zero && M(qs[1]) == One) {
            return 1;
        }
        elif(M(qs[0]) == One && M(qs[1]) == Zero) {
            return 2;
        }
        else{
            return 3;
        }
    }
}

Task 1.6. Distinguish two basis states given by bit strings

問題

入力: Bool 型で記述される長さ $N$ の 2 つのビット列 $a$ と $b$

および $a$ もしくは $b$ と同じ値を持つことが保証されている $N$ 量子ビット

出力: 量子ビットが $a$ と同じ （言い換えると$|a⟩$) なら 0、 $b$ と同じなら 1を返す。

解説

どちらかの古典ビットと同じ値を持つことが保証されているので、一つずつ観測して $a$ と比較し、全て同じなら 0 を、1 つでも違うところがあれば 1 を返せばよさそうです。先にも記載したとおり、観測結果は Result 型なので、Bool と比較するためには変換が必要です。ここでは ResultFromBool という関数を使いました。

operation TwoBitstringsMeasurement (qs : Qubit[], bits1 : Bool[], bits2 : Bool[]) : Int
{
    body
    {
        for(i in 0..Length(qs)-1) {
            if(M(qs[i]) != ResultFromBool(bits1[i])) {
                return 1;
            }
        }
        return 0;
    }
}

Task 1.7. |0...0⟩ state or W state ?

問題

入力: $|00\dots00⟩$ もしくは W 状態であることが保証されている $N$ 量子ビット

出力: 量子ビットが $|00\dots00⟩$ なら 0、W 状態なら 1を返す。

解説

W 状態とは？ と思った方は SuperPosition の復習を。ハミング距離が 1 となる量子ビットが等しい確率振幅で重ねあわされた状態をいうんでしたね。W 状態をつくるのは難しかったのですが、$|00\dots00⟩$ かどうかを判別するだけならどこかに $|1⟩$ があるかどうかだけを見ればいいので、簡単ですね。

operation AllZerosOrWState (qs : Qubit[]) : Int
{
    body
    {
        for(i in 0..Length(qs)-1) {
            if(M(qs[i]) == One) {
                return 1;
            }
        }
        return 0;
    }
}

Task 1.8. GHZ state or W state ?

問題

入力: GHZ 状態もしくは W 状態であることが保証されている $N$ 量子ビット

出力: 量子ビットが GHZ 状態なら 0、W 状態なら 1を返す。

解説

GHZ 状態とは？ と思った方も SuperPosition の復習を。全部 $|0⟩$ か全部 $|1⟩$かが確率 0.5 で重ねあわされた状態を GHZ 状態というんでしたね。GHZ 状態の場合はすべての量子ビットの観測結果が一致するので、同じかどうかを見ていけば判別ができそうです。回答は以下となります。

operation GHZOrWState (qs : Qubit[]) : Int
{
    body
    {
        for(i in 1..Length(qs)-1) {
            if(M(qs[0]) != M(qs[i])) {
                return 1;
            }
        }
        return 0;
    }
}

Task 1.9. Distinguish four Bell states

問題

入力: 下記のいずれかの Bell 状態であることが保証された 2 量子ビット
1. $|\phi^+⟩ = \frac{| 00 \rangle + | 11 \rangle}{\sqrt 2}$
2. $|\phi^-⟩ = \frac{| 00 \rangle - | 11 \rangle}{\sqrt 2}$
3. $|\psi^+⟩ = \frac{| 01 \rangle + | 10 \rangle}{\sqrt 2}$
4. $|\psi^-⟩ = \frac{| 01 \rangle - | 10 \rangle}{\sqrt 2}$

出力:
- $|\phi^+⟩$ なら 0 を返す。
- $|\phi^-⟩$ なら 1 を返す。
- $|\psi^+⟩$ なら 2 を返す。
- $|\psi^-⟩$ なら 3 を返す。

解説

さて、この問題では 4 つの Bell 状態を区別しなければいけません。どうやればいいでしょう？ここで、Bell 状態の作り方について思い出してみると、私たちは $|00⟩$ から $|\phi^+⟩$ を作るためにアダマール ゲートと $\rm CNOT$ ゲートを利用したのでした。なので今度は $\rm CNOT$ ゲートを利用してからアダマール ゲートを利用してやれば、 $|\phi^+⟩$ を $|00⟩$ に収束させることができそうです。同じ操作を他の 3 状態に行うとどうなるでしょうか？

\begin{pmatrix}
|\phi^-⟩ \\
|\psi^+⟩ \\
|\psi^-⟩ 
\end{pmatrix}
= \frac{1}{\sqrt 2}
\begin{pmatrix}
| 00 \rangle - | 11 \rangle \\
| 01 \rangle + | 10 \rangle \\
| 01 \rangle - | 10 \rangle 
\end{pmatrix} \Rightarrow
\frac{1}{\sqrt 2}\begin{pmatrix}
| 00 \rangle - | 10 \rangle \\
| 01 \rangle + | 11 \rangle \\
| 01 \rangle - | 11 \rangle 
\end{pmatrix} \Rightarrow
\begin{pmatrix}
| 10 \rangle \\
| 01 \rangle \\
| 11 \rangle 
\end{pmatrix} 

いずれも特定の状態に収束することが確認できました。これをもとに観測して判定してやればよさそうですね。回答は以下。

operation BellState (qs : Qubit[]) : Int
{
    body
    {
        CNOT(qs[0], qs[1]);
        H(qs[0]);
        if(M(qs[0]) == Zero && M(qs[1]) == Zero) {
            return 0;
        }
        elif(M(qs[0]) == One && M(qs[1]) == Zero) {
            return 1;
        }
        elif(M(qs[0]) == Zero && M(qs[1]) == One) {
            return 2;
        }
        else {
            return 3;
        }
    }
}

Task 1.10*. Distinguish four orthogonal 2-qubit states

問題

入力: 下記のいずれかの状態であることが保証された 2 量子ビット
1. $|S_0⟩ = \frac{|00⟩ + |01⟩ + |10⟩ + |11⟩}{2}$
2. $|S_1⟩ = \frac{|00⟩ - |01⟩ + |10⟩ - |11⟩}{2}$
3. $|S_2⟩ = \frac{|00⟩ + |01⟩ - |10⟩ - |11⟩}{2}$
4. $|S_3⟩ = \frac{|00⟩ - |01⟩ - |10⟩ + |11⟩}{2}$

出力:
- $|S_0⟩$ なら 0 を返す。
- $|S_1⟩$ なら 1 を返す。
- $|S_2⟩$ なら 2 を返す。
- $|S_3⟩$ なら 3 を返す。

解説

一見難しそうにみえますが、実は単純な問題です。まずは $|S_0⟩$ をみてみると、符号はいずれも正で、位相のずれはありません。この状態は $|00⟩$ から双方をアダマールすることで実現できそうです。ほかも見てみましょう。$|S_1⟩$ は 2 ビット目が 1 の時だけ位相が反転しています。これは $|01⟩$ から双方をアダマールしたように見えます。$|S_2⟩$ は逆に先頭ビットが 1 の時だけ位相が反転しているので、$|10⟩$ から双方をアダマールすることで作成できます。ここまでくれば $S_3$ の解説は不要でしょう。
まとめると、観測する前にそれぞれのビットをアダマールすれば各状態を収束させることができます。

operation TwoQubitState (qs : Qubit[]) : Int
{
    body
    {
        H(qs[0]);
        H(qs[1]);
        if(M(qs[0]) == Zero && M(qs[1]) == Zero) {
            return 0;
        }
        elif(M(qs[0]) == Zero && M(qs[1]) == One) {
            return 1;
        }
        elif(M(qs[0]) == One && M(qs[1]) == Zero) {
            return 2;
        }
        else {
            return 3;
        }
    }
}

Task 1.11**. Distinguish four orthogonal 2-qubit states, part two

問題

入力: 下記のいずれかの状態であることが保証された 2 量子ビット
1. $|S_0⟩ = \frac{ |00⟩ - |01⟩ - |10⟩ - |11⟩}{2}$
2. $|S_1⟩ = \frac{-|00⟩ + |01⟩ - |10⟩ - |11⟩}{2}$
3. $|S_2⟩ = \frac{-|00⟩ - |01⟩ + |10⟩ - |11⟩}{2}$
4. $|S_3⟩ = \frac{-|00⟩ - |01⟩ - |10⟩ + |11⟩}{2}$

出力:
- $|S_0⟩$ なら 0 を返す。
- $|S_1⟩$ なら 1 を返す。
- $|S_2⟩$ なら 2 を返す。
- $|S_3⟩$ なら 3 を返す。

解説

似たような問題に見えますが、先ほどのように単純にアダマールするだけでは解けそうにありません。とりあえず、アダマールして項を減らしましょう。

\begin{pmatrix}
|S_0⟩ \\
|S_1⟩ \\
|S_2⟩ \\
|S_3⟩ \\
\end{pmatrix}
= \frac{1}{2}
\begin{pmatrix}
 |00⟩ - |01⟩ - |10⟩ - |11⟩\\
-|00⟩ + |01⟩ - |10⟩ - |11⟩\\
-|00⟩ - |01⟩ + |10⟩ - |11⟩\\
-|00⟩ - |01⟩ - |10⟩ + |11⟩
\end{pmatrix} \Rightarrow
\frac{1}{\sqrt 2}\begin{pmatrix}
 | 10 \rangle - | 01 \rangle \\
-| 00 \rangle + | 11 \rangle \\
-| 10 \rangle - | 01 \rangle \\
-| 00 \rangle - | 11 \rangle 
\end{pmatrix} 

ちょっとはすっきりとしました。ただし、すべて 2 ビットことなる状況なので、もう一度アダマールしても収束しそうにありません。ビットを反転する必要がありそうなので、こういう時は $\rm CNOT$ ですね。

\frac{1}{\sqrt 2}\begin{pmatrix}
 | 10 \rangle - | 01 \rangle \\
-| 00 \rangle + | 11 \rangle \\
-| 10 \rangle - | 01 \rangle \\
-| 00 \rangle - | 11 \rangle 
\end{pmatrix} \Rightarrow
\frac{1}{\sqrt 2}\begin{pmatrix}
 | 11 \rangle - | 01 \rangle \\
-| 00 \rangle + | 10 \rangle \\
-| 11 \rangle - | 01 \rangle \\
-| 00 \rangle - | 10 \rangle 
\end{pmatrix} 

いい感じですね。あとは再度先頭ビットをアダマールすれば収束できそうです。

\frac{1}{\sqrt 2}\begin{pmatrix}
 | 11 \rangle - | 01 \rangle \\
-| 00 \rangle + | 10 \rangle \\
-| 11 \rangle - | 01 \rangle \\
-| 00 \rangle - | 10 \rangle 
\end{pmatrix} \Rightarrow
\begin{pmatrix}
-| 11 \rangle\\
-| 10 \rangle\\
-| 01 \rangle\\
-| 00 \rangle 
\end{pmatrix} 

位相は反転していますが、観測したあとでは特に意味はないので、そこも気にしなくてよさそうです。というわけで回答は以下になります。

operation TwoQubitStatePartTwo (qs : Qubit[]) : Int
{
    body
    {
        H(qs[0]);
        CNOT(qs[0], qs[1]);
        H(qs[0]);
        if(M(qs[0]) == One && M(qs[1]) == One) {
            return 0;
        }
        elif(M(qs[0]) == One && M(qs[1]) == Zero) {
            return 1;
        }
        elif(M(qs[0]) == Zero && M(qs[1]) == One) {
            return 2;
        }
        else {
            return 3;
        }
    }
}

Task 2.1*. |0⟩ or |+⟩ ?

問題

入力: $|0⟩$ か $|+⟩$ であることが保証された量子ビットで、それぞれが発生する確率は等しい

出力: $|0⟩$ なら True を、 $|+⟩$ なら False を返す。なお、このタスクでは 80% 以上の精度で回答すること。

解説

今までは「判別せよ」という問題だったのに、いきなり 80 % 以上の精度で回答せよ （言い換えると、20 % までは間違ってもいい） という問題に変わりました。それもそのはず、BasicGates や SuperPosition を経てブロッホ球が思い浮かぶ方ならわかる通り、$|0⟩$ は真上を、$|+⟩$ は手前を向いています。この状態から双方の量子ビットに同じ操作をして、$|0⟩$ か $|1⟩$ に収束させるということは無理であることが直感的にも理解できるかなと思います。

ではどうすればいいでしょうか？2割は間違ってもいいので、$y$ 軸回りに 45 度回転しちゃいましょう。そうすると、次の図のようになります。

さらに、図の左から $x$ 軸と $y$ 軸を見るとこうなります。

ここから、元々 $|0⟩$ であった量子ビットが再度 $|0⟩$ をとる確率は $\Big(1+\frac{1}{\sqrt 2}\Big)/2.0 \simeq 0.85$ となり、課題の 8 割は達成できそうです。$|+⟩$ が $|1⟩$ となる確率も同じですね。回答は以下です。

operation IsQubitPlusOrZero (q : Qubit) : Bool
{
    body
    {
        Ry(PI() / 4.0, q);
        if(M(q) == Zero) {
            return true;
        }
        return false; 
    }
}

$\pi$ は PI() で取得できる点に注意してください。

Task 2.2**. |0⟩, |+⟩ or inconclusive?

問題

入力: $|0⟩$ か $|+⟩$ であることが保証された量子ビットで、それぞれが発生する確率は等しい

出力: $|0⟩$ なら 0 を、 $|+⟩$ なら 1 を、どちらとも判別がつかなければ -1 を返す。なお、このタスクでは$|0⟩$ の時に 1 と誤回答したり、$|+⟩$ のときに 0 と誤回答することは許されない。ただし、最大 80 % の場合に -1 と回答してよい。また、このタスクでは補助量子ビット（ancilla quibit(s) ）を利用してもよい。

解説

先ほどの問題の亜種です。さっきは適当に観測して間違ってたらごめんね☆で許されたところが、急に厳しい感じですね。間違えないようにするにはどうしたらいいでしょうか？順番に考えていきましょう。

まず、入力そのまま $|0⟩$ か $|+⟩$ の状態を観測したと考えましょう。このとき、$|0⟩$ は定義通り $|0⟩$ しか観測されませんが、$|+⟩$ は 0.5 の確率で $|1⟩$ が観測されます。逆に言えば、$|1⟩$ が観測された場合は初期状態は絶対 $|+⟩$ だったと言えそうです。もしこの観測だけを行うのであれば、絶対 $|+⟩$ だったと言える確率は 0.25 で、残りの 0.75 は -1 を返す羽目になり、要望に合いません。

同じアプローチで、初期状態にアダマールしてみましょう。すると、それぞれ $|+⟩$ か $|0⟩$ になります。今度は $|1⟩$ が観測されたら初期状態は絶対 $|0⟩$ だったといえそうです。この時も絶対 $|0⟩$ だったと言える確率は 0.25 で、残りの 0.75 は -1 を返す羽目になり、要望に合いません。

感の言い方なら既に気づいたかもしれませんが、この 2 つを組み合わせることで回答が可能です。すなわち、確率 0.5 でどちらかの観測を行うのです。そうすれば、$|0⟩$ か $|+⟩$ かを断定できる可能性はそれぞれ 0.125 となり、要件に合います。まあちょっとずるい感じもしますが、回答は以下です。せっかくなので量子ビットを使って確率 0.5 を実現してみました。

operation IsQubitPlusZeroOrInconclusiveSimpleUSD (q : Qubit) : Int
{
    body
    {
        mutable result = -1;
        using (ancilla = Qubit[1]){
            H(ancilla[0]);

            if(M(ancilla[0]) == One) {
                if(M(q) == One) {
                    set result = 1;
                } else {
                    set result = -1;
                }
            } else {
                H(q);
                if(M(q) == One) {
                    set result = 0;
                } else {
                    set result = -1;
                }
            }

            Reset(ancilla[0]);
        }
        return result;
    }
}

最後に

これで Measurement は終了です。筆者は「観測すると重ね合わせ状態が壊れる」くらいの知識しかなかったのですが、一重に観測といっても非常に奥が深いですね。まだまだ観測に関する Kata も登場しそうな気がしました。

次回は何にするか未定ですが、おそらく Deutsch-Jozsa になると思います。いよいよ名前の付いたアルゴリズムや具体的な例が登場し、量子コンピューターの価値がわかるようになってくるはず！