畳み込み演算を用いた残響効果の理論と実装

この記事は Aizu Advent Calendar の5日目の記事です。

• 12/4　後悔
• 12/5　ifft定義に間違いがあったので修正、語弊を招く文章があったので文章校正
• 12/5　ceilの関数定義、nextpow2の説明を修正
• 12/8　出力波形の長さを入力波形の長さとして書き出していた点を修正、結果画像差し替え
• 12/10 ifft定義書き換え

前の人は @misoton665 さんの 軽い気持ちでScalazを使う です。

宣伝

年末に仙台でDJします。

きてね

はじめに

前の年の会津アドベントカレンダーではサウンドプログラミングの先駆けでwavファイルのBPMを解析する記事を書きました（Rubyを使ったWAVファイルのBPM解析）が、今年は本格的にサウンドプログラミングに取り組んでみます。
少し前にRubyによるWAVファイルの音声へのディストーションエフェクト付与って記事も書いたのでこちらも良かったら。
今回は空間系エフェクターの一つであるリバーブの実装、特に畳み込み演算を用いたConvolutionリバーブの実装をRubyで行いたいと思います。
動作環境は以下:

$ ruby -v
ruby 2.2.3p173 (2015-08-18 revision 51636) [x86_64-darwin15]

GitHub:
https://github.com/tspider0176/convolution-reverbrator

リバーブについて

リバーブ（残響）が何なのか分からない人の為に簡単に説明します。と言っても日常に溢れている事象なのでイメージは付きやすいと思います。
風呂場で叫び声を上げた時とかの残響が多分一番良く例に上げられる事象ですが、これは銭湯(会津若松駅前の富士の湯とか)に行ったことある人は良くわかると思います。
他の空間系エフェクトにディレイ、エコーとありますが、イメージ的には

「オアアアアアアアア！！！」
って叫んだ時に
「オアアアアアア！！！！...ォァァァァァァ!!!...ｵｱｱｱｱｱｱ!!!...ｫｧｧｧｧｧｧ!!!」
とエコーして行くのがディレイです。
「オアアアアアアアアァァァァァァンンンンンンﾝﾝﾝﾝﾝﾝ...」
と緩やかに減衰して行くのがリバーブ（残響）です。
以下で詳しく解説されてます。

【今さら聞けない用語シリーズ】リバーブとディレイ、エコーの違い
https://info.shimamura.co.jp/digital/knowledge/2014/01/17108

カラオケでもこう言った空間エフェクトを弄って遊んだことのある人も居るのでは無いでしょうか。
リバーブに話を戻しますが、現状、この残響をハードウェア、ソフトウェア上で実現する為に様々な種類のリバーブが提案されて来てます。
結構深い歴史があるみたいですが趣旨とは外れるので、その種類についてさらっと以下で説明します。

Hall

一番ポピュラーな残響効果。
巨大なコンサートホールを再現した残響効果をもたらす様なリバーブの事。
と言っても実際にコンサートホールを借りて録音なんてとても出来ないので、基本的にはデジタルプラグイン上で実現する。

Room

上のHallリバーブと合わせて箱物リバーブだとか呼ばれてる。
Hallと同じ様な残響効果だが、名前の通りホールよりは狭いスタジオを模したリバーブ効果を指している。
上と同じくデジタルプラグイン上で良く使われている。

Plate

ここから人工的なリバーブの生成法に入る。Plate Reverbは1950年代に誕生。名前から直感的に明らかな様に、鉄板の揺れを利用してリバーブを実現する手法。
デジタル上で再現したプラグインも今なお複数存在している。
ただの鉄板と言っても残響効果を得る為には人の身長か畳一畳分くらいの大きさが必要で、非常に大掛かりな装置になる。

当時は高価だった為金持ちの人しか手に入らなかった様です。

Spring

金属製のバネに振動を加え、その共振で残響効果を得るもの。
1960年に提案、制作された。
Plate Reverbとは違い、比較的狭いスペースでも残響が実現可能。デジタルなリバーブが主流になる前はカラオケの機材にも使われていた。

現在でもギターを触ってる人にとっては結構ポピュラーな存在らしい。
アナログ特有の暖かい残響音が得られるのだとか。

Algorithmic

実際の環境を実現する為に幾つかの（時には膨大な）パラメータを与えて反響を実現する手法。
多くのDigital Audio Workstation (DAW)上のプラグインで用いられている。
色んなツマミを弄って（パラメータを変えて）音を変えるイメージ。
あくまでもパラメータを用いて現実をシミュレートするものの為、クオリティが非常にピンキリ。

現実に存在しない様な環境の反響を実現出来る点には可能性を感じる。
最近流行りのEDM（最近ようやく廃れてきた？）とかで聞く様な「スコォォォォォォオオオオアアアアアアアアンンンンンンンンンンヌ」って音はこの手法じゃないと無理っぽい。

Convolution

Algorithmic Reverbとは対称的に、こちらは実在する環境を元に反響を生成する手法。
具体的には実在する環境の「インパルス応答」と元の音データを畳み込んでリバーブを生成する。
実際に調べてみるとよく上のAlgorithmic Reverbとどっちを使うべきなのかって議論を見かける。
結局適材適所が結論らしい。
反響を再現したい部屋のインパルス応答が存在すれば実際にその部屋で音を鳴らした時の反響をPC上で「完璧に」再現可能。
じゃあそのインパルス応答はどうやって手に入れるのって話になるが、専用の機材を買わなくても以下のサイトの様に無償で配布されている場所もある。（このサイトでは全国各地の教会とか大学の講堂中心）
http://www.openairlib.net/auralizationdb

非常に高品質なリバーブを再現する事もできるが、
インパルス応答の長さが長ければ長いほどそのまま愚直に畳み込み演算を行うと膨大な計算時間が必要になる。
例えば一般的に用いられるサンプリング周波数48000Hzで1秒のインパルス応答を畳み込む場合、 1サンプルの出力を得る為には1秒間に48000回*48000回=23億400万回の積和演算回数が必要。
そこで高速フーリエ変換（FFT）と逆高速フーリエ変換(iFFT)を用いて実現する。

理論的に数学知識モリモリって感じで面白そうだったので学部時代の知識の復習も兼ねて本記事ではこれを実装してみます。

実装する上で理解しておく必要がある理論

インパルス応答と畳み込み演算

インパルス応答

以下引用
インパルスと呼ばれる非常に短い信号を入力したときのシステムTの出力。インパルスとは、時間的幅が無限小で高さが無限大のパルスを示す。実際のシステムでは、テスト用の入力として完全なインパルスを生成するのは不可能。したがって、インパルスの近似として短いパルスを使う。そのパルスがインパルス応答に比較して短ければ、その結果は理論上のインパルス応答に十分近いと言える。(引用:Wikipedia)

これだけでは何のこっちゃ分からないですが、
ざっと調べ回って見たところ、以下の点を頭に入れておけば良さそうです。

あるシステム$T$について、システム$T$に対する入力$f(t)$についての出力$g(t)$を$T[f(t)] = g(t)$と表す時、以下の性質を満たすとする。

• 線形性
  • 入力が2倍になれば出力も2倍に（以下が成立）

T[a \cdot f(t)] = a \cdot T[f(t)] = a \cdot g(t)

• 時不変性
  • 時間に関らず同じ入力には同じ出力（以下が任意の$t_{0}$について成立）

T[f(t - t_{0})] = g(t - t_{0})

まずこれを満たすようなシステム、入力、出力を前提として頭に入れておきます。

畳み込み演算

出力$f(t)$をインパルス（単位）とすると、$g(t)$をインパルス応答と呼ぶ。通常、インパルスは$\delta(t)$、インパルス応答は$h(t)$と表されます。
また、この線形時不変システム$T$の出力$y(t)$はインパルス$\delta(t)$とインパルス応答$h(t)$の畳み込み演算で表され、

y(t) = \sum_{k = - \inf}^{\inf} \delta(k) h(t - k)

と書く事が出来ます。
インパルス応答さえ知っておけばシステムの出力が把握出来る感じですね。インパルス応答すごい。

実装

例えば上の数式は以下の様な関数として実装出来るでしょう。

def y(t)
  (-Float::INFINITY..Float::INFINITY).map{|k| delta[k] * h[t - k]}.sum
end

また、Rubyには畳み込み演算を実現するメソッドEnumerable#injectが既に用意されています。
injectを用いた場合の実装は以下の様になりそうです。

def y(t)
  (-Float::INFINITY..Float::INFINITY).inject(0){|acc, k| acc + (delta[k] * h[t - k])}
end

個人的に愚直に思いつくのは上のコードですが、取り敢えずこの二つの書き方が出来るという事で覚えておきましょう。

※12/5追記
今回Convolution Reverbを実装するに当たって採用したサンプリング・リバーブ法では、周波数領域で畳み込みを行うので、上のコードはどこにも使いません。
何故実装したのか。

高速フーリエ変換(FFT)

大学の講義TAで腐るほど問題は見てきましたが、理論が怪しいのでそもそもフーリエ変換って何の為に使うのってところから軽く復習。

そもそもフーリエ変換は何を変換しているのか？

一言で言えば「時間領域」と「周波数領域」の変換をしている。
通常、グラフ上で我々は横軸を時間として考えているが、フーリエ変換を行うと横軸が周波数になる。

フーリエ変換の何が嬉しいのか？

この世の全ての波形はsin波の合成として見ることが出来る（オイラーの発見より）ので、例えば音の波形から周波数帯域別の強度を表したスペクトルアナライザへの変換が可能になる。
どの帯域の音が鳴っているかが一目で分かるので曲作りには必要不可欠。
他にもCTスキャンだとかの医療分野にも利用されているとか。
フーリエ変換強過ぎる。もうちょっとちゃんと講義を履修すれば良かった。
ただ、実際にリアルタイムで流される音声の周波数を解析する場合は、ある程度速度も重要な要素となって来ます。
そこで次の節で説明する高速フーリエ変換が役に立ちます。

高速フーリエ変換

簡単に言えばフーリエ変換を高速に動作させるアルゴリズムであり、良くFFTと呼ばれる。
より詳しく言えば、離散フーリエ変換(DFT)を高速に行うアルゴリズムであり、対象となる信号が周期的であるということを仮定し、フーリエ変換を行うものになります。
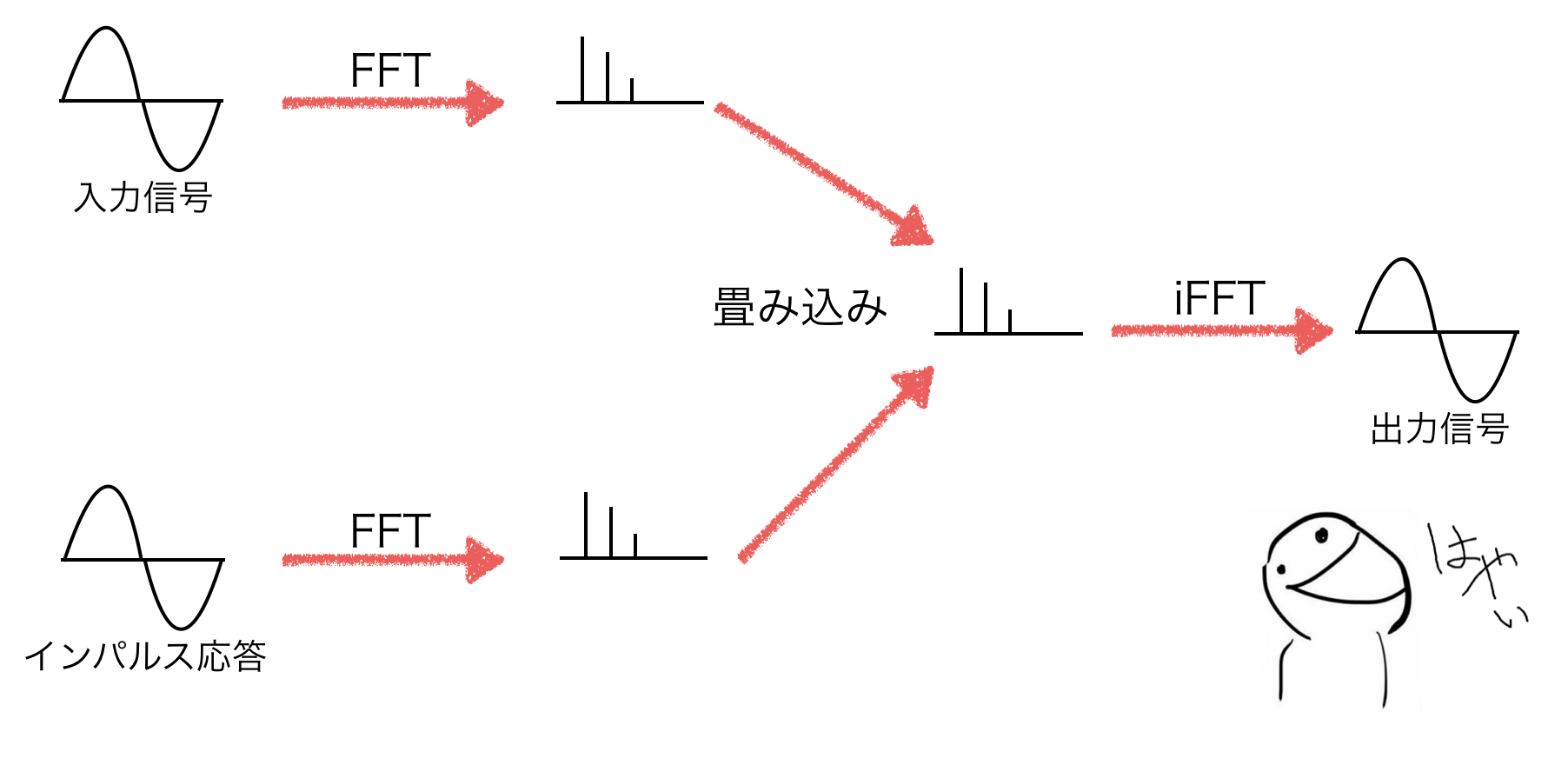
ここでようやく記事の本題に入りますが、インパルス応答を周波数領域で畳み込むサンプリング・リバーブ法というアルゴリズムの存在があります。

サンプリング・リバーブ法

手順を示す簡単な図を下に作りました。

時間領域では畳み込みが必要でしたが、フーリエ変換により周波数領域に落とし込み演算を行う為、単にベクトルを掛け合わせるだけで済みます。

ここで、iFFTとはFFTの逆変換のことであり、通常のフーリエ変換とは逆に「周波数領域」から「時間領域」への変換を表します。
長い入力信号が与えられた場合でも、overlap-add法やoverlap-save法と言った手法が提案されています。説明が長くなってきたので実装パートで触れるとしてここでは割愛します。

以上の点を踏まえて、この記事の目的であるConvolution Reverbの実装は大きく分けて以下のステップで実装出来そうです。

• STEP 1. インパルス応答の長さ調節
  • STEP 1.1. 長さを2の累乗に拡張、それをフレーム長Nとする
  • STEP 1.2. 更に長さを2Nに拡張
• STEP 2. 入力波形の長さを調節
  • STEP 2.1. 入力波形をフレーム長で分割
  • STEP 2.2. overlap-save法に適用する為に先頭にN要素の零配列を結合
• STEP 3. 畳み込み
  • STEP 3.1. 予めインパルス応答をFFT
  • STEP 3.2. 入力波形を2フレームだけ抜き出しFFT
  • STEP 3.3. 周波数領域でインパルス応答と入力波形を畳み込み(積)
  • STEP 3.4. 畳み込み結果を逆高速フーリエ変換で時間領域へ変換
  • STEP 3.5. 円状畳み込み結果を破棄し、直線上畳み込みのみを結果として保持
  • STEP 3.6. 末尾に到達するまでSTEP 3.2から繰り返し

Convolutionリバーブの実装

実際にSTEPに従って順番に実装して行きます。

STEP 1. インパルス応答の長さ調節

まず最初にインパルス応答をFFTした後にoverlap-save法を適用する為に、インパルス応答を適切な長さに調節する必要があります。
順番にして行きましょう。

STEP 1.1. 長さを2の累乗に拡張、それをフレーム長Nとする

まず最初に、FFTの対象となる配列は要素数が2の累乗でなければなりません。
ひとまず現在の配列の要素数を取得します。

impulse.length

次に現在のインパルス応答の長さ以上かつ、最小の2の累乗の値を求めます。
ここではMatlabの全く同じ動作をするnextpow2, ceilという関数を参考に実装しました。

rubyでは例えば以下の様に書くことが出来るでしょう。

def ceil(f)
  f.to_i + 1
end

def nextpow2(n)
  ceil(Math.log2(n))
end

関数ceilは与えられた数値以上の最も近い整数を返す関数（e.g. 1.3が与えられたら2を返す関数）で、nextpow2は与えられた数以上で最も近い2の累乗の指数を返す関数（e.g. 17が与えられたら5を返す関数）です。
以上の関数を使えば、フレーム長Nは以下の様に書けるでしょう。

N = 2**nextpow2(impulse.length).to_i

ここでインパルス応答を長さNの配列に拡張（末尾は0埋め）したいので、以下の様に書きました。

def zeros(n)
  Array.new(n, 0)
end

new_impulse = impulse + zeros(N - impulse.length)

この0で埋めるという操作、畳み込みをする準備段階で結構何回も使うので先を見越してさっさと関数zerosに切り分けました。
ここで実装した関数名zerosもPythonのnumpyライブラリから取ってきています。Python最高。

STEP 1.2. 更に長さを2Nに拡張

さて、長さNのインパルス応答は手に入りました。
次に後々に使うoverlap-save法でインパルス応答を入力波形を畳み込みをする際に長さを合わせなければならないので、更にインパルス応答の長さを2Nまで拡張します。
今回は前半を0埋めしました。

new_impulse_n2 = zeros(N) + new_impulse

※後半を0埋めnew_impulse_n2 = new_impulse + zeros(N)しても問題ありません。
後々のSTEP3.5にて破棄する部分が変わるだけです。

STEP 2. 入力波形の長さを調節

次に上で求めたフレーム長と新しく生成したインパルス応答を元に入力波形の長さを調節します。

STEP 2.1. 入力波形をフレーム長で分割

最初に、入力波形をSTEP 1.1で求めたフレーム長Nで分割します。
イメージ的には下の図の様になります。

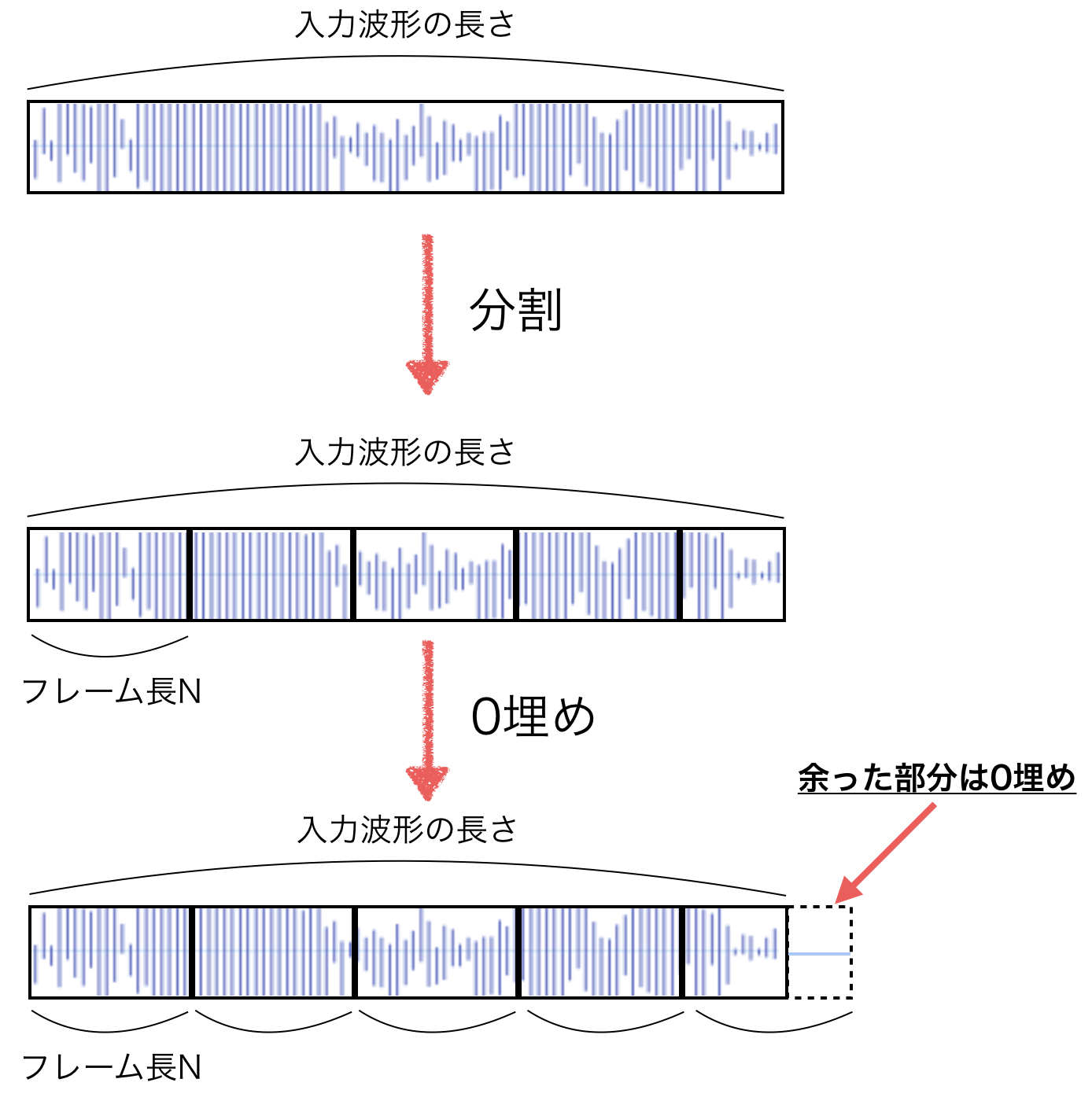
実装してみましょう。
まずフレーム数を求めます。（上の図ではフレーム数5）
入力された波形をinput、フレーム長を$N$とすると、フレーム数$k$は以下の式で計算出来るので

k = \frac{input.length}{N} + 1 \\
 = \frac{input.length + N}{N}

プログラムでは

frame_num = ceil((input.length + N) / N.to_f).to_i

と書けるでしょう。
フレーム数が求まったことにより、拡張された入力波形を求めることが出来ます。

new_sig_length = N * frame_num

STEP 2.2. overlap-save法に適用する為に先頭にN要素の零配列を結合

次にインパルス応答のSTEPで行った様に、畳み込みする際に用いるoverlap-save法用に配列を拡張します。
前の節で簡単に説明しましたが、改めてサンプリング・リバーブ法に使われるoverlap-save法について説明します。
具体的には以下の図の様にプロセスが進みます。

拡張入力波形から2N分取り出して処理を行うというプロセスになっていますが、実際に畳み込みを行った後に残響効果が得られるのはN ~ 2N-1の範囲の波形のみです。（図で緑の枠で囲った場所）
ここで問題となってくるのは、今の拡張入力波形のままでは一番最初の2フレームから畳み込みを開始した場合、0 ~ N-1までの範囲にある波形の残響効果が得られ無くなってしまう点が挙げられます。
じゃあどうするのかという話ですが、単純に拡張入力波形を更にN分だけ拡張します。

new_signal = zeros(N) + input + zeros(new_sig_length - input.length - N)

前半部分に更にフレーム数N分だけ0を追加することによって、残響効果が入力波形の最初から適用されるようになります。

以上で前準備であるインパルス応答と入力波形の拡張が終わりました。
次からいよいよ本題である畳み込みに入ります。

STEP 3. 畳み込み

再掲

STEP 3.1. 予めインパルス応答をFFT

上の図から分かる通り、拡張入力波形は最初から最後まで2Nずつフレームをずらして畳み込み演算していく必要がありますが、インパルス応答については最初から最後まで同じ波形をそのまま畳み込みに使うことが出来ます。
なので、インパルス応答は予めFFTを行って周波数領域に変換して置きましょう。

取り敢えずFFTとiFFTから実装してみます。
が、今回は時間が無かったのでFFTに関しては以下のサイトからソースコードをお借りしました。
リンク：http://d.hatena.ne.jp/ku-ma-me/20111124/p1

def fft(a, tf = 1)
  n = a.size
  return a if n == 1
  w = Complex.polar(1, -2 * Math::PI / n)
  a1 = fft((0..n / 2 - 1).map { |i| a[i] + a[i + n / 2] }, tf)
  a2 = fft((0..n / 2 - 1).map { |i| (a[i] - a[i + n / 2]) * (w**i) }, tf)
  a1.zip(a2).flatten
end

iFFTに関しては良さそうなソースコードが見つからなかったので、ここでちゃんとFFTの定義を見直してみました。
複素関数$f(x)$の離散フーリエ変換である複素関数$F(t)$は以下で定義されます。

F(t) = \sum_{x = 0}^{N-1} f(x) e^{-i\frac{2\pi t x}{N}}

また逆変換は

f(x) = \frac{1}{N} \sum_{t = 0}^{N-1} F(t) e^{i \frac{2 \pi t x}{N}}

となります。
この数式から分かる様に、単純にFFTの結果に$\frac{1}{N}$をかけて符号を反転するだけでしたので、以下の様にfft関数とifft関数を実装し直しました。

def fft(a, tf = 1)
  n = a.size
  return a if n == 1
  w = tf == 1 ? Complex.polar(1, -2 * Math::PI / n) : Complex.polar(1, 2 * Math::PI / n)
  a1 = fft((0..n / 2 - 1).map { |i| a[i] + a[i + n / 2] }, tf)
  a2 = fft((0..n / 2 - 1).map { |i| (a[i] - a[i + n / 2]) * (w**i) }, tf)
  a1.zip(a2).flatten
end

# ※12/6修正
def ifft(a, n)
  fft(a, -1).map{|x| x / n}
end

これでインパルス応答のfft結果を手に入れることが出来ました。

impulse_fft = fft(new_impulse_n2)

STEP 3.2. 入力波形を2フレームだけ抜き出しFFT

STEP 3.3. 周波数領域でインパルス応答と入力波形を畳み込み(積)

次に入力波形の畳み込みの前準備に入ります。
このステップは一気に書いてしまいます。
入力波形に関しては、「拡張入力波形から2フレーム抜き出して拡張インパルス応答と掛け合わせる」という操作を先頭から末尾まで行う必要があります。
つまり、フレーム数を$k$と置くと、全体で$k-1$回の計算が必要なので、以下の様に書けるでしょう。

(0...k).map{|i|
  start_point = N * i
  end_point = N * (i + 2)

  part_fft = fft(new_signal[start_point...end_point])
}

実際にプログラムを追記すると、

(0...k).map{|i|
  start_point = N * i
  end_point = N * (i + 2)

  # convolution new_signal[start_point...end_point] with impulse
  part_fft = fft(new_signal[start_point...end_point])
  convolution = part_fft.zip(impulse_fft).map { |f, s| f * s }
}

以上の様に書けるでしょう。
zip_withメソッドを実装すればもっと綺麗に書けたのですが取り敢えず今回はこの形にしておきます。

STEP 3.4. 畳み込み結果を逆高速フーリエ変換で時間領域へ変換

STEP3.3で手に入った畳み込み結果を逆高速フーリエ変換で時間領域へと移し、実数部分のみを取り出します。

res = ifft(convolution, 2 * N).map(&:real)

STEP 3.5. 円状畳み込み結果を破棄し、直線上畳み込みのみを結果として保持

STEP1.2で軽く触れた通り、拡張インパルス応答を作成する際に先頭か末尾どちらを0埋めしたかによってここの操作は変わってきます。
今回は前半を0埋めしたので、畳み込み結果の前半が直線上畳み込み結果、後半が円状畳み込み結果となっています。
なので、

res[0...N]

で直線上畳み込み結果のみを取得することが出来るでしょう。

STEP 3.6. 末尾に到達するまでSTEP 3.2から繰り返し

以上のSTEP3の内容を拡張入力波形の末尾まで走査し終わるまで続けます。
今までのコードをまとめると以下の様になります。

r = (0...frame_num - 1).map{ |i|
  start_point = N * i
  end_point = N * (i + 2)

  part_fft = fft(new_signal[start_point...end_point])
  convolution = part_fft.zip(impulse_fft).map { |f, s| f * s }

  res = ifft(convolution, 2 * N).map(&:real)

  res[0...N]
}.flatten

最後に手に入れた配列から、入力配列の長さ分だけの配列を切り取れば加工済みの音源が手に入ります。

r[0...input.length]

まとめ

以上のステップで作成したソースコードの全貌は以下の様になります。
以下のコードではwavが符号付きShort型で入力された時の事を考慮しているので、要所要所でインパルス応答及び入力波形値の正規化（値域を-1 ~ 1へ）を行っています。

def ceil(f)
  f.to_i + 1
end

def nextpow2(n)
  ceil(Math.log2(n))
end

def zeros(n)
  Array.new(n, 0)
end

def fft(a, tf = 1)
  n = a.size
  return a if n == 1
  w = tf == 1 ? Complex.polar(1, -2 * Math::PI / n) : Complex.polar(1, 2 * Math::PI / n)
  a1 = fft((0..n / 2 - 1).map { |i| a[i] + a[i + n / 2] }, tf)
  a2 = fft((0..n / 2 - 1).map { |i| (a[i] - a[i + n / 2]) * (w**i) }, tf)
  a1.zip(a2).flatten
end

def ifft(a)
  fft(a, -1).map{|x| x / a.length}
end

N = 2**nextpow2(impulse.length).to_i
new_impulse = impulse + zeros(N - impulse.length)
new_impulse_n2 = zeros(N) + new_impulse
new_impulse_n2 = new_impulse_n2.map { |i| i / SIGNED_SHORT_MAX.to_f }

frame_num = ceil((input.length + N) / N.to_f).to_i

new_sig_length = N * frame_num
new_signal = zeros(N) + input + zeros(new_sig_length - input.length - N)
new_signal = new_signal.map { |i| i / SIGNED_SHORT_MAX.to_f }

impulse_fft = fft(new_impulse_n2)

r = (0...frame_num - 1).map{ |i|
  start_point = N * i
  end_point = N * (i + 2)
  part_fft = fft(new_signal[start_point...end_point])

  convolution = part_fft.zip(impulse_fft).map { |f, s| f * s }

  res = ifft(convolution).map(&:real)

  res[0...N]
}.flatten

new_wavs = r[0...new_sig_length]

結果

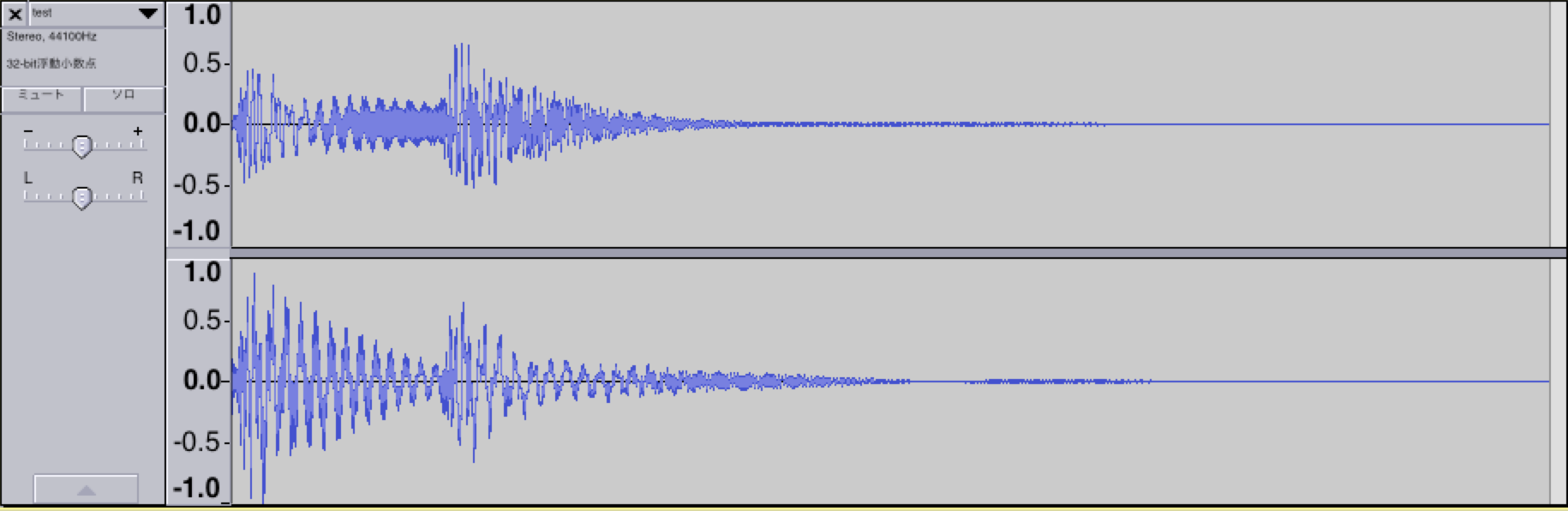
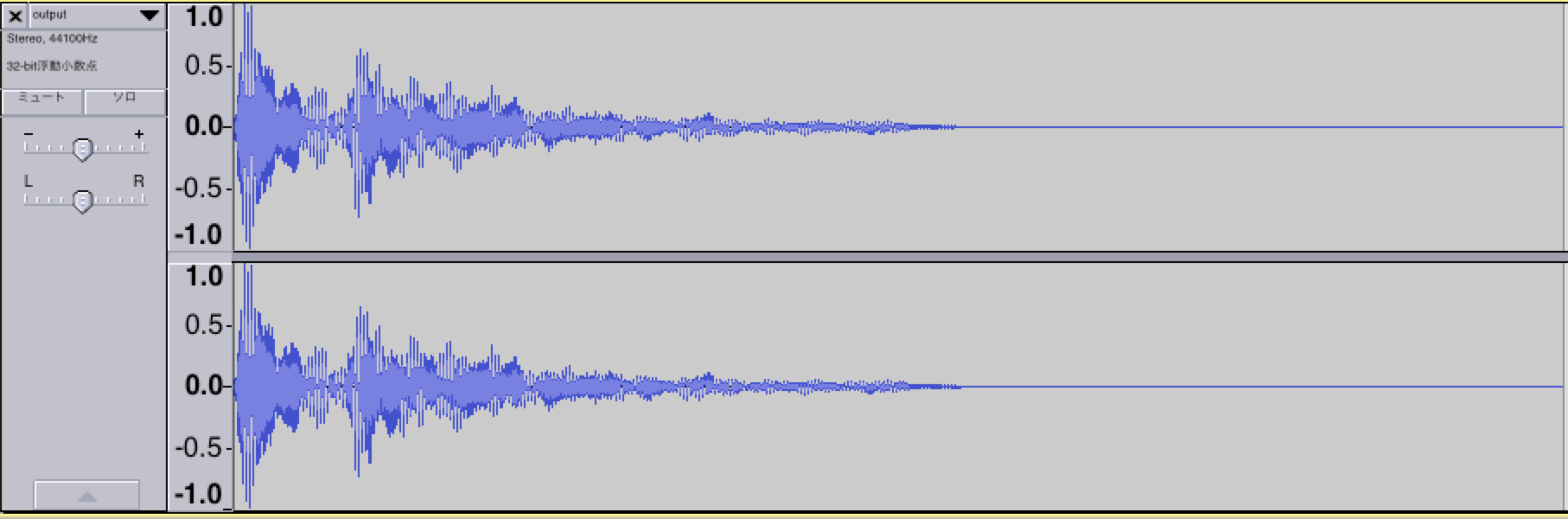
適当にインパルス応答のサンプルと効果音を拾ってきて実際に実行してみました。
Qiita上では音楽ファイルを貼り付けることは出来ないっぽいので入力波形と出力波形から感じ取ってください。

入力波形

インパルス応答

出力波形

今後

• 速度が遅い
  めっちゃ遅い。何が高速なのか分からないくらいには高速フーリエ変換が遅い。多分アルゴリズムが問題。
  引用元にも書かれてましたが改善の余地はかなりあるっぽいので調べる。

• クリッピングに関する処理が無い。
  上の波形を見て分かる通り、出力波形が一部音割れしている。
  Signed Shortを超えた場合の処理を書く必要あり。
  ※12/7 GitHub修正。

• ソースコードが汚い
  きたない。オブジェクト指向したい。
  ※12/7 GitHub修正。

• 単体テストが無い
  そのうち書く。

最後に

アドベントカレンダー書かないとダメじゃんって事に気付いたのが4日前くらいだったので正直このテーマを選んだことに後悔しました。
が、実際に進めていくにつれてあやふやだった知識の再確認（特にフーリエ変換！）が出来たのと、やっぱりサウンドプログラミング楽しいって事が実感出来てとても良かったです。
おそらくこの記事を上げた後にもアップデートを繰り返して行くと思いますが、今回は取り敢えず動くものが出来た、という時点で上げさせて貰いました。
最後まで読んで頂きありがとうございました。

次の人は @Takabatake_Y さんです。
宜しくお願いします。

Reference

https://www.g200kg.com/jp/docs/dic/convolutionreverb.html
http://www.ari-web.com/service/soft/reverb-4.htm
http://yukara-13.hatenablog.com/entry/2013/12/20/094926
http://brian-doyle.com/2011/10/28/convolution-vs-algorithmic-reverbs/
http://www.wave.ie.niigata-u.ac.jp/yamaguchi/education/basic_research/spectrum_signal_processing.pdf
https://en.wikipedia.org/wiki/Reverberation
https://en.wikipedia.org/wiki/Fast_Fourier_transform