はじめに
ビットコインの価格低下が続いています。昨年はバブルだったので、適正価格?に戻りつつあるだけなのかもしれません。
しかし気になるのは、ここ1ヶ月ほどでハッシュレートが急低下していることです。ハッシュレートの低下は51%攻撃の可能性を高めるという見方もあり、心配です。
本記事では、定量的なインセンティブ分析を行い、51%攻撃がどのような条件で成立しうるかと、その費用等について考えたいと思います。
(ここでは大量のハッシュパワーを投入してブロックチェーンの書き換えを行う攻撃を総称して「51%攻撃」と記述しています。実際には51%以下でも攻撃は成立します)
先に結果の概要を書いておきます:
- 長期期待利益が下がると正直なマイニングのインセンティブが低下する
- 特に赤字マイナーは攻撃に傾きやすく、機材も入手しやすいため危険
- ハッシュシェア20%程度でも攻撃のインセンティブが出てくる
注意して分析したつもりですが、間違いや関連研究がありましたら、ぜひコメントやSNS等でお知らせください。
なお、本記事は何らかの投資判断を勧めるものではなく、読者の投資判断について筆者は一切の責任を負いません。
復習:二重支払いの過程
ある商人に対して二重支払いをする過程は下記のようになります:
- はじめに、攻撃者は同一コインに対する2つのトランザクションを用意します。
- 一つは商人への送金トランザクションで、これはメインチェーンにブロードキャストします。
- もう一つが自分への送金トランザクションで、これは密かに分岐させた攻撃者チェーンに含めます。こちらは公開しないまま採掘を進めます。
- 商人はメインチェーン上で一定の承認回数を待ってから、商品を渡します。
- 攻撃者は商品を受け取ったことを確認したのち、次のステップに進みます。
- 攻撃者は攻撃者チェーンがメインチェーンよりも長くなるまで採掘を続けたのち、攻撃者チェーンを公開します。
- 攻撃者チェーンがインチェーンを上書きします。
- 結果として、商人への送金トランザクションがなくなり、自分への送金トランザクションが残ります。攻撃者はコインを手元に残したまま、商品を手に入れることができます。
- 二重支払いそのものの収入とは別に、ネットワーク毀損による値下がりを見越して空売りすることで、収入を得ることができます。
静的な分析
サトシナカモトはどう分析したか
Satoshiは、この問題を2段階に分けて表現しています。
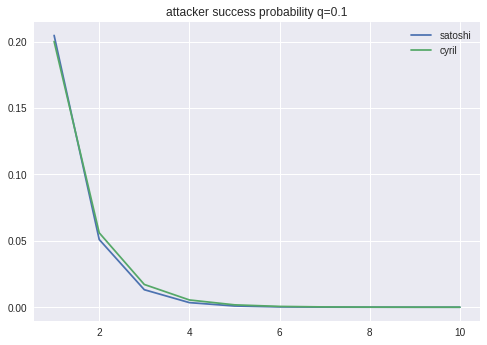
第1段階は、攻撃者がzブロックの遅れから追いつく確率を求めています。これは「ギャンブラー破産問題」と呼ばれる古典的な問題と同等で、答えが知られています。
q_z = \left\{
\begin{array}{}
1 & (p \leq q) \\
(q/p)^z & (else)
\end{array}
\right.
この時点で、攻撃者のハッシュパワーが50%以上になると、成功率が100%になることがわかります。後で詳しく述べますが、この100%という数字は注意して解釈する必要があります。
第2段階は、zブロック承認された取引が覆される確率について近似計算しています。
メインチェーンがzブロック進む平均時間だけ経った時点での攻撃者のブロック高は、$\lambda = z \frac{q}{p}$ としたポアソン分布で表すことが出来ます。ここから追いつく確率は第1段階で求めていますので、これを組み合わせてブロック書換えが成功する確率を計算しています。
p_{satoshi}(q,z) = 1- \sum_{k=0}^{z} \frac{\lambda^k e^{-\lambda} }{k!}(1-(q/p)^{z-k})
pythonコードで書くと:
def attacker_success_probability_satoshi(q,z):
p = 1-q
l = z*(q/p)
s = 1.0
for k in range(0,z+1):
poisson = np.exp(-l)
for i in range(1,k+1):
poisson *= l/i
s -= poisson*(1-(q/p)**(z-k))
return s
サトシナカモトの分析の誤り
上記の第二段階において、確率的に決まるはずの承認時間を平均値1点で近似している箇所に、誤りが指摘されています(参考記事、論文)。論文を見ると様々なケースの結果がありますが、Satoshi論文に対応する攻撃成功確率の正しい計算方法のみpythonコードで書きだしておきます:
from scipy.special import comb
def attacker_success_probability_cyril(q,z):
p = 1-q
s = 1
for k in range(0,z):
s -= (p**z*q**k-q**z*p**k)*comb(k+z-1,k)
return s
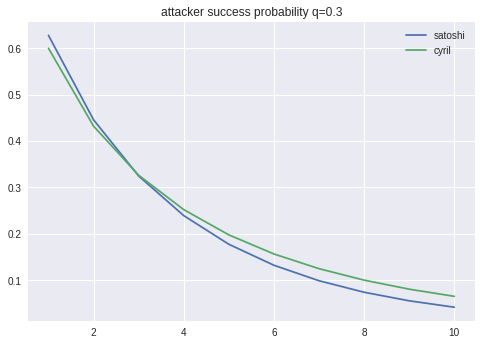
いくつかプロットして比較すると、確かに多少の乖離が見られます。
詳しく知りたい方は元論文を見てください(私は拾い読みしただけです)。
静的な分析の限界
上記の分析は、$t\rightarrow\infty$の極限を考えた、いわば静的な分析であることに注意が必要です。成功するまで攻撃し続けることが想定されています。ハッシュパワーを維持するには電気代がかかりますので、これは現実的ではありません。また、攻撃が長期に渡るのはメインチェーンが偶然先に伸びるような場合で、そのときは攻撃の期待値が小さくなりそもそものインセンティブがなくなるタイミングがあるかもしれません。
静的な分析は、ワーストケースの分析としては十分意味がありますが、これでは現実的なインセンティブの分析はできません。
動的な分析
インセンティブは主に収入・費用・確率で決まりますので、これらを動的な形で定式化していきます。
攻撃者の戦略を考慮することで、より正確な攻撃インセンティブを見積もることができますし、攻撃途中の動的な分析を行うことで、攻撃にかかる平均的な費用を見積もることができます(確率分布として分析することもできると思いますが、今回は平均値で考えます)。
また、法定通貨建てに換算して考えることで、のコイン価格下落の影響を考慮できるようになります。
(以前、戦略を考慮した2重支払いのインセンティブ分析を行いましたが、今回はより詳細かつ現実的な設定で動的な分析をしています)
分析に必要なパラメータ
分析に必要なパラメータは下記の関数コメントに記載しています。以下で補足説明しますが、ひとまず掲載しておきます(コード本体は記事末尾に掲載します):
def attacker_incentive(Z, Hc, Hmain, Hattack, E, C, R, P0, P1, X, G, strategy="optimal", D=12, B=200, Tblock=600, Tstep=6):
"""
Satoshiの分析と同様に追いつく事を攻撃成功の条件としているが、実際はブロック高が追いつくだけでは確実な攻撃にならないことに注意
Parameters
----------
Z: 攻撃者が書き換えようとするブロック数
Hc: 基準ハッシュパワー PHash/s ディフィカルティから導出可能
Hmain: メインチェーンのハッシュパワー PHash/s
Hattack: 攻撃者のハッシュパワー PHash/s
E: 計算エネルギー KJ/PHash
C: 電気代 USD/KWh
R: ブロック採掘報酬+期待手数料 BTC
P0: 攻撃前のコイン価格 USD/BTC
P1: 攻撃実現後のコイン価格 USD/BTC
X: 攻撃実現により得られる収入 USD
G: Tblockあたりの割引率
strategy: 戦略 honest/attack/optimal
D: 解析時間 hour
B: 分析ブロック数上限
Tblock: ブロックタイム sec
Tstep: 解析ステップ時間幅 sec
Returns
----------
t: 攻撃開始からの時刻 hour
income: 各時刻での平均収入 USD
cost: 各時刻での平均費用 USD
prob: 各時刻での成功確率 USD
V: 状態価値 USD
S: 方策
"""
攻撃成功時の収入
もし攻撃が実現するとコインの価格は暴落すると考えられ、$P_0\gt P_1$となります。2重支払いしたコインおよび攻撃開始後に得たブロック報酬は$P_1$で売却することになります。
暴落を見越したコインの空売りなどでも収入を得ることが出来ますが、分析の中では2重支払いと空売りを区別する必要はありませんので、これらの攻撃による収入の合計を$X$としておきます。
長期的な期待利益
前記の価格暴落が長期的な期待利益へ与える影響はどのように表現したらよいでしょうか。
ここでは、長期的な利益は攻撃前後とも正直なマイニングを継続することで得られると考えられます。あるブロックでの正直なマイニングの収益性は、$f$を攻撃失敗または攻撃成功(それぞれ0,1)として、下記のように書けます:
a_f = \frac{H_{attack}}{H_{attack}+H_{honest}}RP_f-EH_{attack}C\frac{T_{block}}{3600} \\
マイニングの収益性は、マイニング設備の進化などにより月日が経つほど下がる傾向があるはずです。多少雑ではありますが、これをブロックあたりの割引率$G$で表現すると、等比級数の和の式から長期の期待利益は$A_f = a_f/(1-G)$となります。
例えば1日あたりの利益が1USDで1年で収益性が半減する設定なら、$a_0 = 1/(624)$、$G = 0.5^{1/(624*365)}$となり、結果として$A_0$は約527USDとなります。
状態空間
インセンティブを分析するために、攻撃途中の状態を定式化します。
メインチェーンのブロック高を$i$、攻撃者チェーンのブロック高を$j$とし、$0\leq i,j \lt B$とします。
$Z$ブロック書き換える攻撃の成功条件は$max(i,Z) \leq j$です(実際は等号なしが正確だと思いますが、Satoshiの分析条件にあわせています)。この条件を満たした場合、それ以降は(攻撃)成功状態とし、攻撃成功よりも先に$i = B$になった場合、それ以降は(攻撃)失敗状態とします。
十分に短い時間ステップ$T_{step}$での状態遷移を考えれば、複数ブロックが同時に発見される確率を無視でき定式化がシンプルになります。
なお、$B$は攻撃成功率が頭打ちになる頃の平均ブロック高よりも多めに設定しておけば、分析精度が確保できるはずです。
最適な方策
攻撃者は、それぞれの状態で停止・正直なマイニング・攻撃継続のいずれかの行動を選ぶことができます。例えばメインチェーンが攻撃者チェーンよりも先に伸びているような状態では、攻撃を停止することが最適になり得るのは直感的にもわかります。最適な行動パターン(方策といいます)は下記のように導出することができます。
最適な方策の導出にあたり、状態価値関数を導入します。状態価値観数は各状態からのある方策をとったときの将来の期待利益を計算したものです。
まず、失敗状態の状態価値は$A_0$、成功状態の状態価値は$A_1$にブロック報酬を足した$A_1+jRP_1$と置けます。その他の状態価値は、次に進む状態の状態価値とその遷移確率を表す下記の式から逆算することができます:
\begin{align}
V^{stop}_{ij} &= (1-P)V^{stop}_{ij}+PV_{i+1 j} \\
V^{honest}_{ij} &= (1-P-Q)V^{honest}_{ij}+PV_{i+1 j}+Q(V_{i j+1}+RP_0)-W \\
V^{attack}_{ij} &= (1-P-Q)V^{attack}_{ij}+PV_{i+1 j}+QV_{i j+1}-W \\
V_{ij} &= max(V^{stop}_{ij},V^{honest}_{ij},V^{attack}_{ij})
\end{align}
ここで$Q,P$はそれぞれ攻撃者チェーンとメインチェーンのステップ時間あたりのブロック発見確率、$W$はステップ時間あたりのコストで、いずれも与えたパラメータから簡単に計算できます。
行動が最適な方策$S_{ij}$の要素は、上記4つ目の式のmaxをargmaxに置き換えれば計算することができます(この問題では状態の巡回がないのでこの方法で解けます)。
攻撃開始時点での状態価値$V_{00}$の値を攻撃の初期費用と比較することで、攻撃のインセンティブがあるかどうかがわかります。
時間推移の計算
攻撃にかかる典型的な費用を見積もるために時間推移も計算します。
各時刻における状態の確率分布を、離散確率分布$M_{ij}$および累積成功確率$M_{success}$、累積失敗確率$M_{fail}$で表します。
前記で計算した各$i,j$での行動$S_{ij}$を反映したうえで遷移確率をかけていけば、$M$全体の時間推移を計算することができます。計算過程は数式で書いてもわかりにくいのでコードを参照してください。
$M$の時間推移がわかれば、目的であった平均収入・平均費用・成功確率それぞれの時間推移を計算することができます。
静的な分析との比較
攻撃優先の戦略を取った際の攻撃成功確率の時間変化をいくつかプロットし、静的な分析との整合性をチェックしておきます。
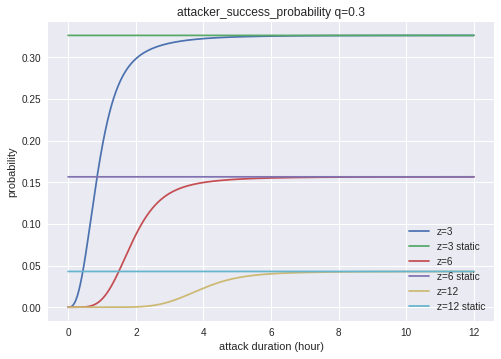
q=0.3の結果を見ると、時間が経つにつれて静的な分析(Cyrilの結果)に正確に漸近していることがわかります。
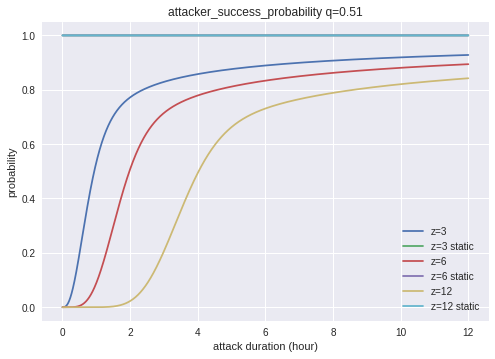
51%攻撃にあたるq=0.51の結果は下記となります。12時間経った時点での攻撃の成功確率は一般的な承認時間のz=6の場合で90%程度にとどまっています。このことから、51%攻撃を確実に成功させるには相当なコストと時間を用意しなければならないことがわかります(コストについては後で別の分析をします)
結果
前置きが長くなってしまいましたが、結果を見ていきます。
ここでは次の数値を共通の仮定とします(価格とハッシュレートは2018/12/1付近での状況を想定しています)。
Z = 10 # 攻撃者が書き換えようとするブロック数
Hc = 38000 # 基準ハッシュパワー PHash/s ディフィカルティから導出可能
R = 13 # ブロック採掘報酬+期待手数料 BTC
P0 = 4100 # 攻撃前のコイン価格 USD/BTC
P1 = P0*0.8 # 攻撃実現後のコイン価格 USD/BTC
G = 0.5**(1/6/24/365) # ブロックあたりの割引率
C = 0.1 # 電気代 USD/KWh
下記の値は都度与えることとします。
q: 攻撃者チェーンのシェア
E: 計算エネルギー KJ/PHash
X: 攻撃実現により得られる収入 USD
なお、特に断らない限りASIC取得費などの初期費用を考慮に入れていないことに注意してください。
攻撃のインセンティブが発生する条件
まずは全体像を把握しましょう。
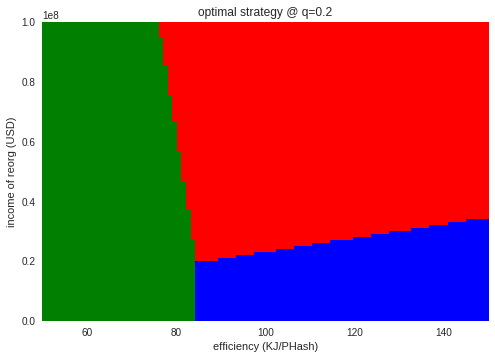
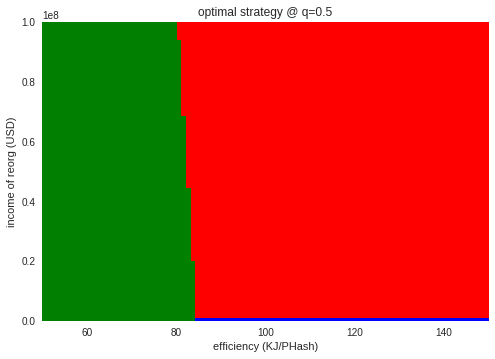
攻撃者のハッシュシェア$q$・攻撃の収入$X$・マイニング機器のエネルギー効率$E$の3変数を動かしたときの最適な戦略を見てみます。それぞれのマップは各パラメータにおける最適な行動を示しています。青が停止、緑が正直なマイニング、赤が攻撃です。
$X=0$の領域(最下端の領域です)では攻撃のインセンティブは存在しないことと、マイニング継続と停止の境界が$E=85$付近であることがわかります。
そして全体を見ると、$E=85$付近の左右どちら側か(マイナーの損益)によって、大きく戦略が異なることもわかります。
続いて、黒字・赤字マイナーそれぞれの詳細な分析結果を見ていきます。
ケースA 黒字マイナー
新型のマイニング機器を利用しており黒字が維持できているマイナーを考えます。例えばAntminerS11はおおよそ、ハッシュパワー20.5TH/s、消費電力1530Wですので、$E=74.6$であり黒字になります。
上記と同様、攻撃の今度は$q$と$X$を動かして最適な戦略を見てみます。
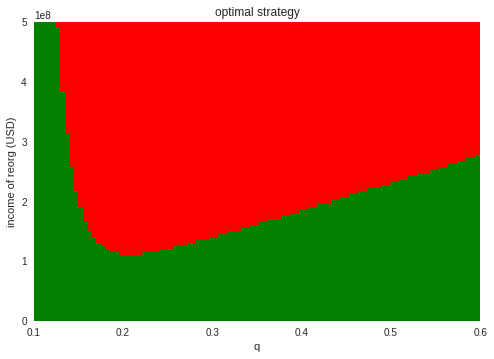
$X$が1億ドル程度から、攻撃が最適な戦略になってきます。
意外なことに、$q=0.2$付近で、攻撃のインセンティブが出てきやすいようです。
次に2つのケースを設定し、最適方策と時間推移を詳細に見ていきましょう。
ケースA-1 ハッシュシェアが高い場合
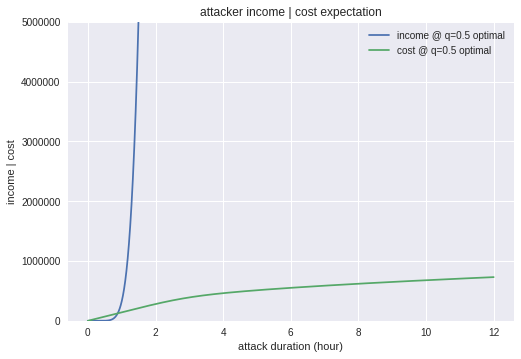
$q=0.5$、攻撃収入は3億ドルとしましょう。
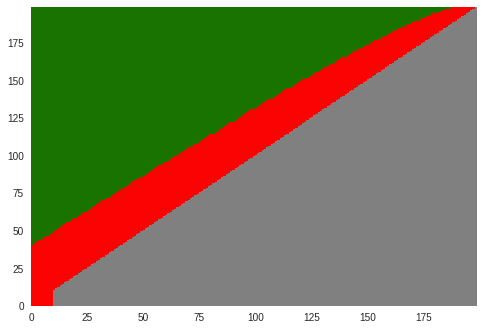
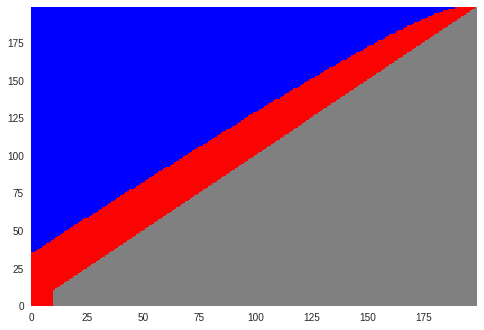
今度は方策を見てみましょう。横軸が攻撃者チェーンのブロック高、縦軸がメインチェーンのブロック高です。灰色の領域は到達しない領域で、その他はこれまでと同様の意味です。
メインチェーンが大きくリードした場合はメインチェーンに戻るような方策ですが、今の設定は$q=0.5$ですのでハッシュパワーは均衡しており、$i=j$のラインから大きくはずれることは稀です。したがって、実際には殆ど攻撃を継続するような動きになりいます。
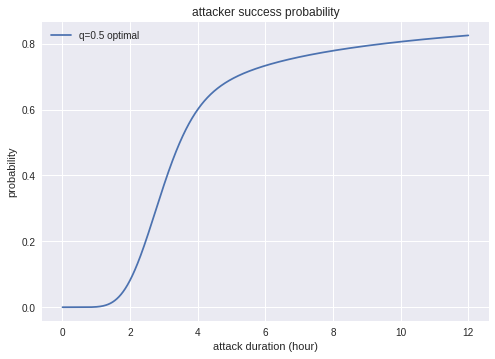
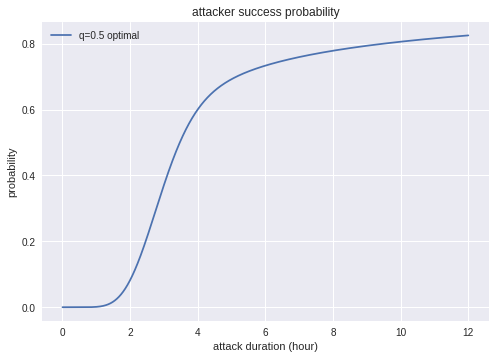
攻撃の成功率です。攻撃の成功率は高く、10時間時点で80%を超えています。
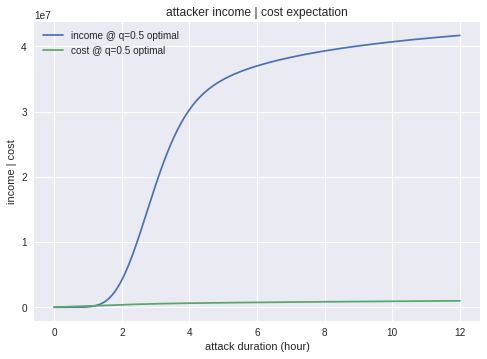
収入と費用です。収入は成功率と同様の立ち上がりで、費用の方は見えなくなってしまっています。
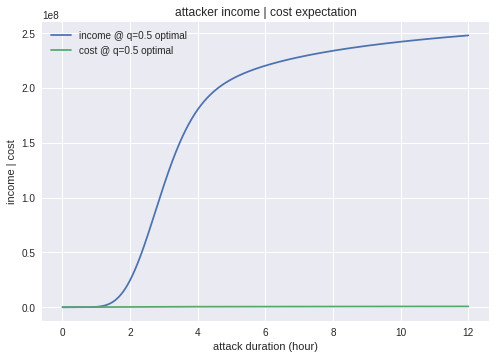
費用を見るためにy軸を拡大しますと、攻撃を維持するコストは100万ドル程度であることがわかります。
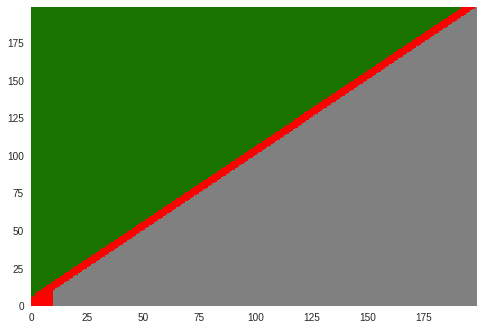
ケースA-2 ハッシュシェアが低い場合
$q=0.2$、攻撃収入は3億ドルとしましょう。
方策を図にすると下記のようになります。シェアが高いときと比べ、ほそぼそと攻撃するような方策です。
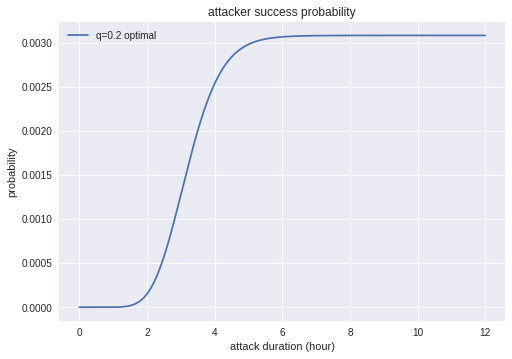
攻撃の成功率です。0.3%程度と非常に小さい値です。
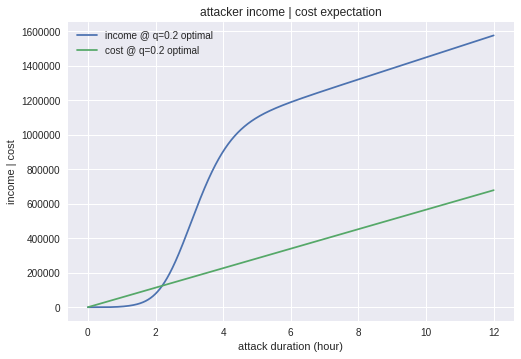
収入と費用です。
はじめの2時間程度は費用が収入を上回っていますが、次第に攻撃成功分の期待値が重なってきます。
概ね攻撃開始から5時間程度のところまで来ると、あきらめて正直なマイニングに切り替えているようです。
ケースB 赤字マイナー
旧型のマイニング機器を利用しており赤字になってしまっているマイナーを考えます。なお、もし十分な供給があればですが、Nicehash等でハッシュパワーを調達する場合も類似の結果になるでしょう。発送電設備や土地建物など不要のため、より効率的に攻撃できるかもしれません。
例えばAntminerS9iはおおよそ、ハッシュパワー14.0TH/s、消費電力1400Wですので、$E=100$であり赤字になります。
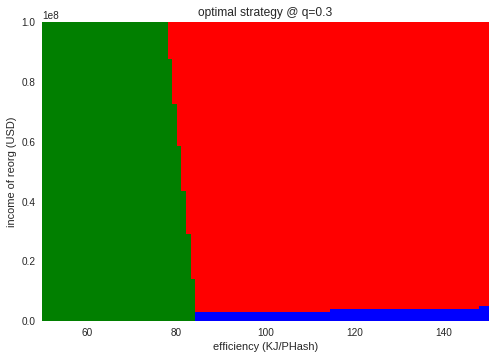
再度、$q$と$X$を動かして最適な戦略を見てみます。
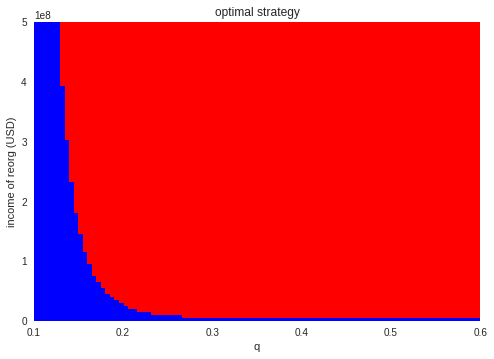
黒字マイナーのケースよりも低い数千万ドル程度の攻撃収入額で、攻撃が最適となっています。
ここでも黒字マイナーの場合と同様、最適方策と時間推移を見てみます。
ケースB-1 ハッシュシェアが高い場合
$q=0.5$、攻撃収入は5000万ドルとしましょう。
正直なマイニングが選ばれないことを除くと、概ねケースA-1と類似の傾向ですので、解説は省略します。
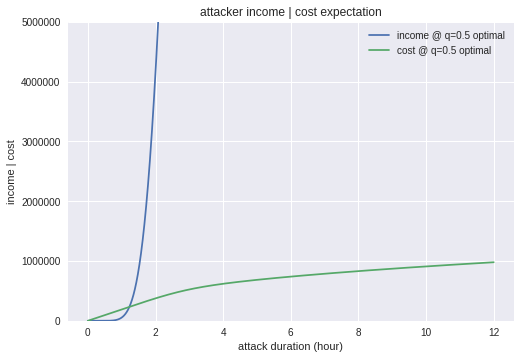
ケースB-2 ハッシュシェアが低い場合
$q=0.2$、攻撃収入は5000万ドルとしましょう。
こちらも概ねケースA-2と類似の傾向ですが、攻撃収入の設定金額を下げているのもありますが、期待利益は5万ドル程度になってしまいました。これは攻撃収入で仕掛けた5000万ドルに対して、リスクの割にリターンが小さいように思えます。
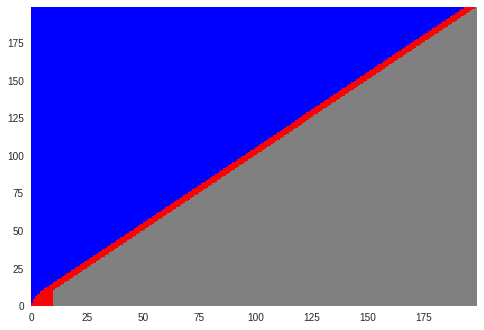
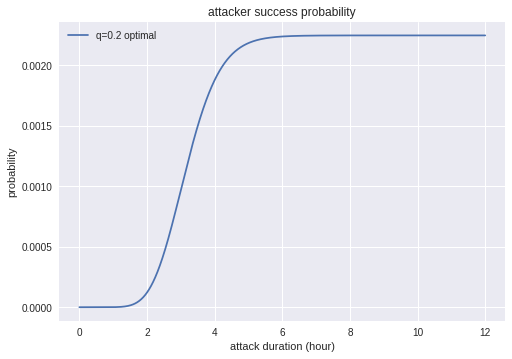
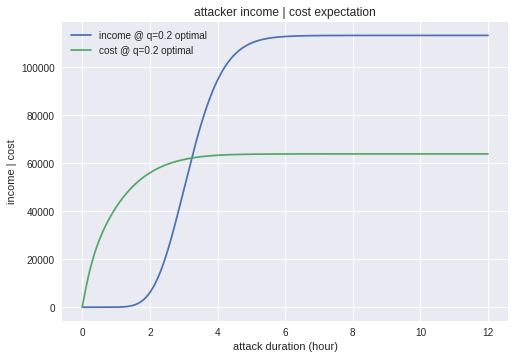
ケースB-2追加 方策の比較
ついでに、ケースB-2について、最適方策と攻撃優先の方策がどのように異なるか見ておきましょう。
まず、成功確率は攻撃優先の場合のほうが高くなります。
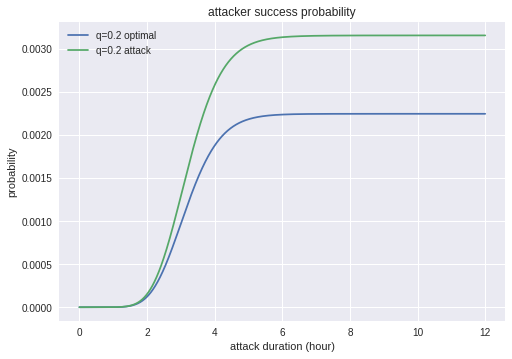
一方収入と費用を見てみると、攻撃優先の場合は収入は大きくなるものの、攻撃のコストがかかり続けるため利益が出ることは無いということが確認できます。
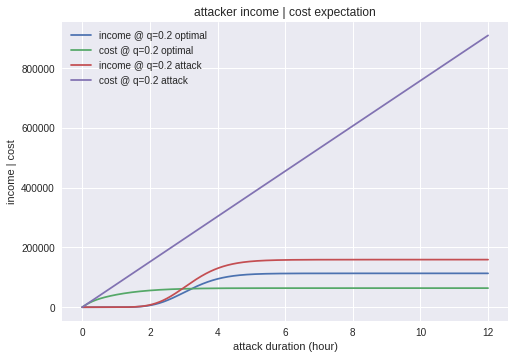
考察とまとめ
黒字のマイナーは、攻撃が実現すると長期的な期待利益に悪影響が出るため、攻撃のインセンティブが正直なマイニングのインセンティブを上回ることが難しくなります。それでも数億ドルレベルの攻撃収入を仕込んだ際には、攻撃のインセンティブが出始めます。
対して赤字のマイナーは、失うものがないため攻撃のインセンティブが現れやすく、1千万ドル程度の攻撃収入であっても攻撃のインセンティブが出てきます。攻撃そのものの期待収入や攻撃成功率は黒字マイナーの場合と大差ありませんが、赤字になるようなASICは安価に手に入れることができるかもしれませんので、その意味で攻撃の実現性は出やすいかもしれません。NiceHashなどで赤字レベルのハッシュパワーを大量購入しての攻撃もありえます。
いずれの場合でもハッシュシェア50%を取ることができればある程度確実に攻撃を成功させられますが、実際にそれだけの数のASICを手に入れるのは難しいと思われます。あるいは、攻撃のインセンティブが出始めるハッシュシェア20%程度は確保できる可能性が高まりますが、その場合の攻撃成功確率は0.3%といったレベルで、実際に攻撃を実行するにはリスクが大きいものになります(期待値自体はプラスですので、巨額の予算があれば問題ないかもしれません)。そしてそもそも数千万ドル〜数億ドルといった攻撃収入を空売りや2重支払いで仕掛ける必要があります。取引所や送金ではこの程度の額が日常的に動いてはいますが、これだけの資金を用意できる人は限られてくるでしょう。
感覚的には51%攻撃の実現性はあまり大きくないように思えます。
(おまけ)赤字マイナーの攻撃を防ぐ方法?
二重支払い自体の成功確率を減らすには、広く理解されているように承認数を増やすのが一番簡単な対策です。
では、ネットワーク毀損(空売り)のインセンティブにはどのような対策ができるでしょうか。
少し考えてみると、なかなかトリッキーな方法が有り得ることがわかります。それは、旧型のASICを入手して破壊するという方法です。これは攻撃者よりも大きい買いポジションを持っている人にとって十分なインセンティブがありそうに思えます。ただ、実際には他の人に率先してこれを行うインセンティブは無いですし、攻撃の画策があるかないかも不透明ですので、実現性は薄いと思います。
(おまけ2)51%攻撃に関連しそうなイベント
51%攻撃に関係しそうなイベントを記載しておきます。
51%攻撃のインセンティブに関係する条件:
- マイニングの長期的な期待利益の低下
- 価格低下
- 規制
- 事件
- 撤退マイナーの増加
- 価格低下
- 半減期
- 新型ASICの発売
- ハッシュレートの低下
攻撃準備に関係する条件:
- 撤退したハッシュパワーの収集
- ハッシュパワーの取引量増加
- 旧型ASICの取引量増加
- 収入源の確保
- 巨額の送金を頻繁に行う
- 先物や取引所の取引高増加
コード
記事中のグラフを再現できるipynbはこちらにありますが、関数部分はここにも掲載しておきます:
import numpy as np
import cv2
import matplotlib.pyplot as plt
def attacker_success_probability_satoshi(q,z):
if q>0.5:
return 1
p = 1-q
l = z*(q/p)
s = 1.0
for k in range(0,z+1):
poisson = np.exp(-l)
for i in range(1,k+1):
poisson *= l/i
s -= poisson*(1-(q/p)**(z-k))
return s
# ref: https://arxiv.org/abs/1702.02867
from scipy.special import comb
def attacker_success_probability_cyril(q,z):
if q>0.5:
return 1
p = 1-q
s = 1
for k in range(0,z):
s -= (p**z*q**k-q**z*p**k)*comb(k+z-1,k)
return s
from functools import lru_cache
@lru_cache(2000)
def attacker_incentive(Z, Hc, Hmain, Hattack, E, C, R, P0, P1, X, G, strategy="optimal", D=12, B=200, Tblock=600, Tstep=6, skip_simulation=False):
"""
Satoshiの分析と同様に追いつく事を攻撃成功の条件としているが、実際はブロック高が追いつくだけでは確実な攻撃にならないことに注意
Parameters
----------
Z: 攻撃者が書き換えようとするブロック数
Hc: 基準ハッシュパワー PHash/s ディフィカルティから導出可能
Hmain: メインチェーンのハッシュパワー PHash/s
Hattack: 攻撃者のハッシュパワー PHash/s
E: 計算エネルギー KJ/PHash
C: 電気代 USD/KWh
R: ブロック採掘報酬+期待手数料 BTC
P0: 攻撃前のコイン価格 USD/BTC
P1: 攻撃実現後のコイン価格 USD/BTC
X: 攻撃実現により得られる収入 USD
G: Tblockあたりの割引率
strategy: 戦略 honest/attack/optimal
D: 解析時間 hour
B: 分析ブロック数上限
Tblock: ブロックタイム sec
Tstep: 解析ステップ時間幅 sec
skip_simulation: 時間シミュレーションをスキップするかどうか
Returns
----------
t: 攻撃開始からの時刻 hour
income: 各時刻での平均収入 USD
cost: 各時刻での平均費用 USD
prob: 各時刻での成功確率 USD
V: 状態価値
S: 方策
"""
N = int(D*3600/Tstep) # ステップ数
# honestマイニングの長期期待利益
# 長期的には難易度調整でHcによらない値となる
q = Hattack/(Hmain+Hattack)
A0 = (P0*R*q-E*Hattack*C*Tblock/3600)/(1-G)
A1 = (P1*R*q-E*Hattack*C*Tblock/3600)/(1-G)
# 解析ステップ時間内にブロックを発見する確率
P = (Tstep/Tblock)*(Hmain/Hc)
Q = (Tstep/Tblock)*(Hattack/Hc)
# 状態価値テーブルと戦略テーブル
V = np.zeros((B,B))
S = 9 + np.zeros((B,B),dtype=np.int32) # 0:stop, 1:honest, 2:attack, 9:N/A
# 終了状態以降の戦略
if strategy == "optimal" or strategy == "attack":
S_fail = 1 if A0>0 else 0
S_success = 1 if A1>0 else 0
elif strategy == "honest":
S_fail = 1
S_success = 1
else:
pass
# 境界値の決定
for k in range(B):
V[B-1,k] = max(0,A0)
j = max(Z,k)
V[k,j] = j*R*P1+X+max(0,A1) # mature期間があるのでP1で換金
# 貪欲法による導出
W = E*Hattack*C*Tstep/3600
for i in range(B-1)[::-1]:
for j in range(max(i,Z))[::-1]:
vh = ((P+Q)*V[i+1,j] + Q*R*P0 - W)/(P+Q) # honest->attackという戦略がないことを仮定して問題ない
va = (P*V[i+1,j] + Q*V[i,j+1] - W)/(P+Q)
V[i,j] = max(0,vh,va)
if strategy == "optimal":
if V[i,j] == 0:
S[i,j] = 0
elif V[i,j] == vh:
S[i,j] = 1
elif V[i,j] == va:
S[i,j] = 2
elif strategy == "honest":
S[i,j] = 1
else:
S[i,j] = 2
# 出力
income = np.zeros((N,)) # 各時刻での平均収入
cost = np.zeros((N,)) # 各時刻での平均費用
prob = np.zeros((N,)) # 各時刻での攻撃成功率
if not skip_simulation:
# 状態の表現
M = np.zeros((B,B)) # 攻撃成功前の各状態の確率分布 dim0がメインチェーン、dim1が攻撃者チェーンのブロック高を表す
M_fail = 0 # 累積の失敗率
M_success = 0 # 累積の成功率
M[0,0] = 1 # 初期状態
# 条件ごとのインデックスを事前計算
i_success, j_success = np.arange(B), np.maximum(np.arange(B),Z)
i_stop, j_stop = np.where(S==0)
i_honest, j_honest = np.where(S==1)
i_attack, j_attack = np.where(S==2)
# 状態遷移の計算
for n in range(N):
M1 = np.copy(M)
# honestブロックが進む場合
d = P*M[(i_stop,j_stop)]
M1[(i_stop+1,j_stop)] += d
M1[(i_stop,j_stop)] -= d
d = (P+Q)*M[(i_honest,j_honest)]
M1[(i_honest+1,j_honest)] += d
M1[(i_honest,j_honest)] -= d
d = P*M[(i_attack,j_attack)]
M1[(i_attack+1,j_attack)] += d
M1[(i_attack,j_attack)] -= d
# attackerブロックが進む場合
d = Q*M[(i_attack,j_attack)]
M1[(i_attack,j_attack+1)] += d
M1[(i_attack,j_attack)] -=d
# 収入と費用の見積もり
p_honest = np.sum(M[(i_honest,j_honest)])
p_attack = np.sum(M[(i_attack,j_attack)])
p_success = np.sum(M1[(i_success,j_success)])
income[n] = p_honest*Q*R*P0 + np.sum(M1[(i_success,j_success)]*j_success)*R*P1 + p_success*X
cost[n] = (p_honest+p_attack)*W
if S_success == 1:
income[n] += M_success*Q*R*P1
cost[n] += M_success*W
if S_fail == 1:
income[n] += M_fail*Q*R*P0
cost[n] += M_fail*W
prob[n] = p_success
# 終了状態の更新
M_fail += np.sum(M1[B-1])
M1[B-1] = 0
M_success += p_success
M1[(i_success,j_success)] = 0
M = np.copy(M1)
t = np.arange(N)*Tstep/3600 # 経過時間 hour
return t, income, cost, prob, V, S
# ref: https://qiita.com/kenmatsu4/items/fe8a2f1c34c8d5676df8
from matplotlib.colors import LinearSegmentedColormap
cmap_bgr = LinearSegmentedColormap.from_list('custom_cmap', [(0.0,"blue"),(0.1,"green"),(0.2,"red"),(1.0,"gray")])