空間分割とは
シューティングゲームの弾の衝突判定について考えてみましょう。自機が赤い丸、敵の弾があおい丸だとしましょう。下の例の場合、弾の数は20個なのでそこまで判定に時間がかからないので、全部の弾に対して衝突判定を行っても時間がかかりません。しかし、1000個・10000個と弾の数が増えてしまうと全部の弾に対して判定を行っていると時間がかってしまいます。しかし工夫次第で実行時間を短くすることができます。
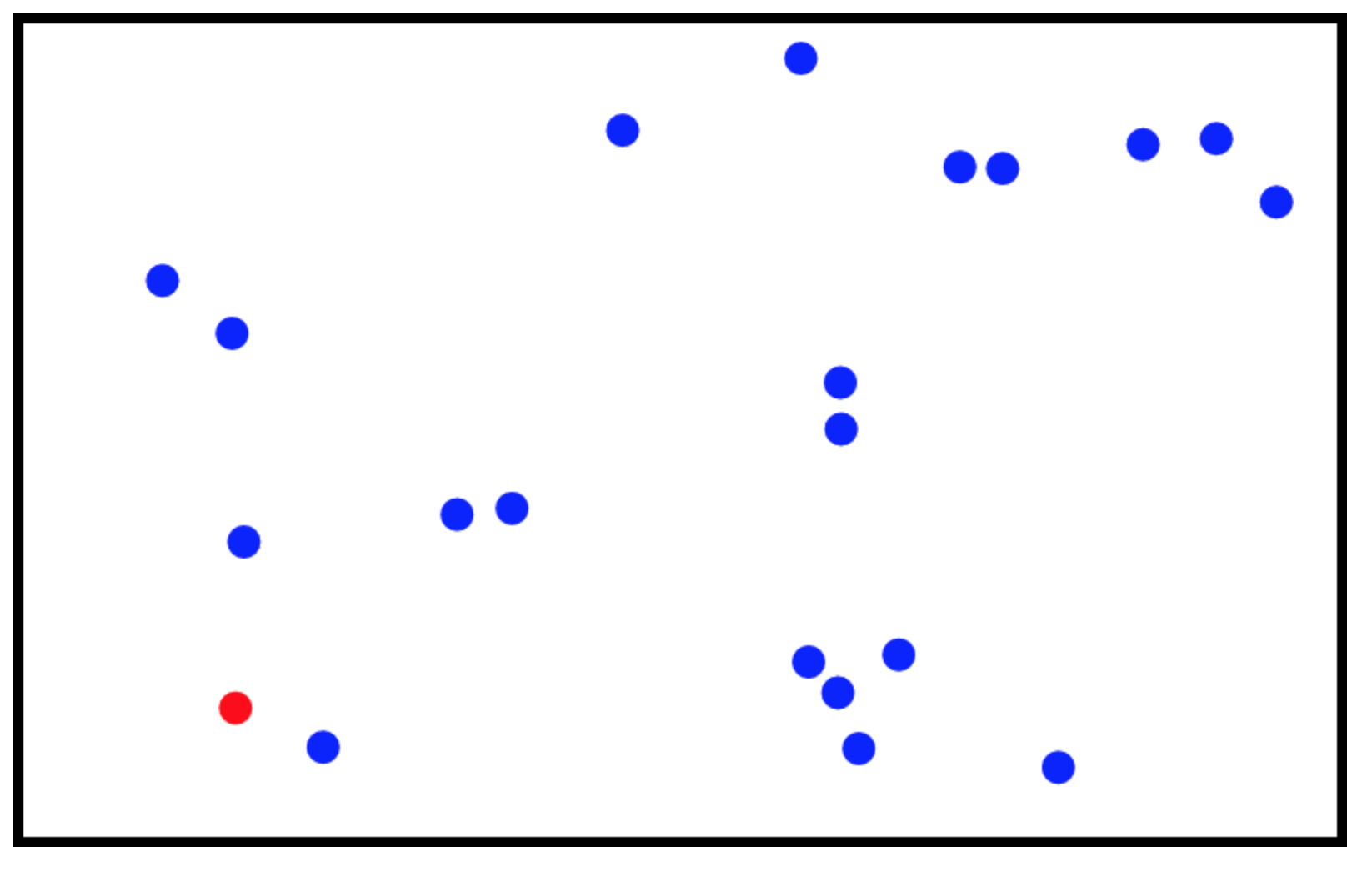
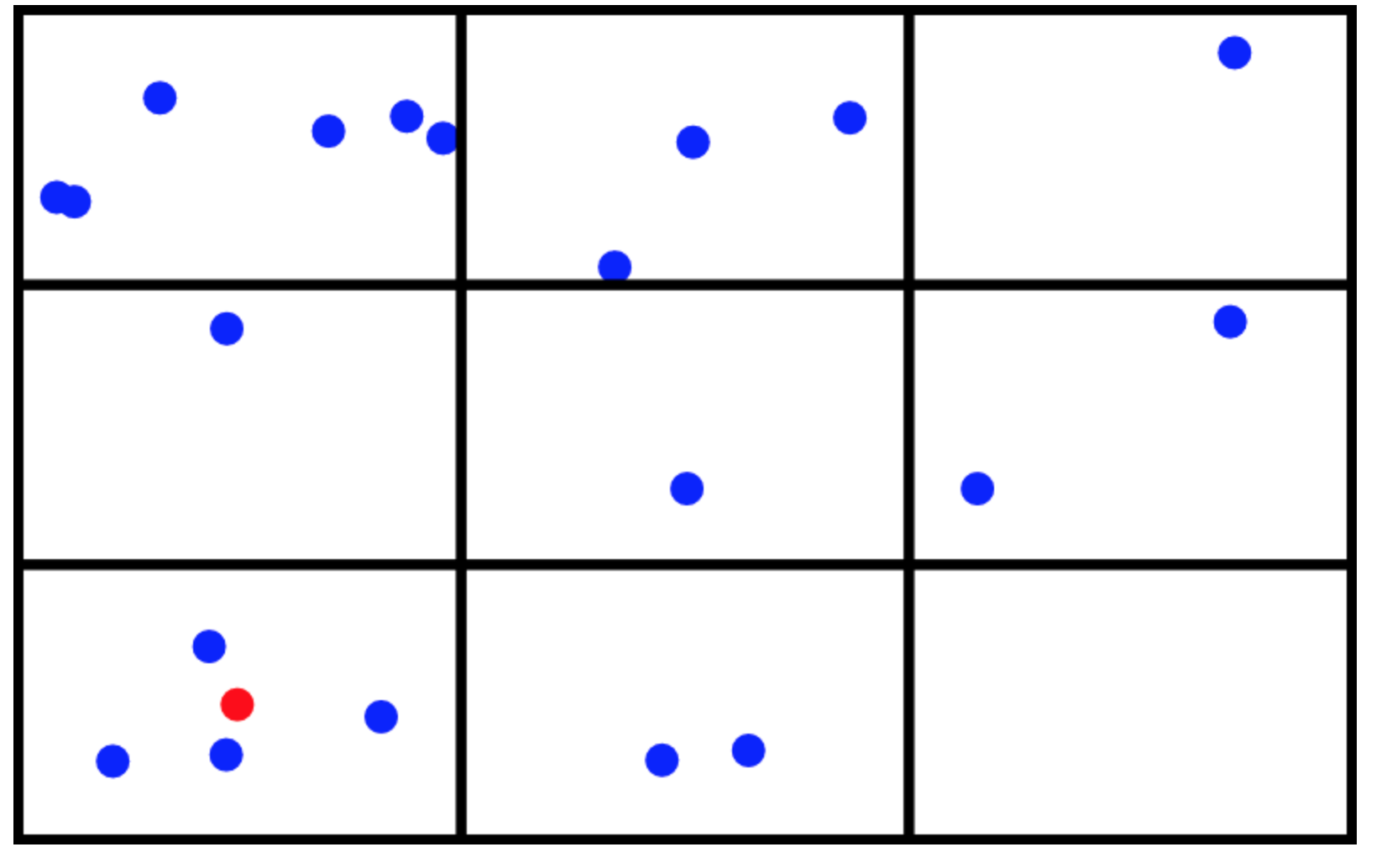
例えば、自機は今左下にいるので、右下/左上/右上にある弾は判定をしなくても良さそうです。自機に近い弾だけを判定する方法を考えます。長方形のケーキを9等分するように、画面縦に3等分、横に3等分をしてみましょう。そうすると分割されたもののうち左下の長方形の中のことだけを考えれば良さそうです。これを使えば一定半径以内にいる弾の情報も簡単に取得できます。この場合、9分割したので計算時間は$
1 / 9 $になります。これが空間分割です。
サンプルコード
JavaScriptで衝突判定を行ってみました。参考程度に見てください。まずは愚直に書いたループです。
let width = 800;
let height = 500;
// 画面の真ん中に自機がいる
let jiki = {x: width / 2.0, y: height / 2.0};
let bullets = [];
for(let i = 0; i < 8; ++i){
// 自機から半径20離れた場所に弾を設置
let theta = i * 2 * Math.PI / 8;
let bullet = {x: width / 2.0 + Math.cos(theta) * 20, y: height / 2.0 + Math.sin(theta) * 20};
bullets.push(bullet);
}
let is_shot = false;
for(let bullet of bullets){
//自機と弾のユークリッド距離を計算
let distance = Math.sqrt(Math.pow(bullet.x - jiki.x, 2) + Math.pow(bullet.y - jiki.y, 2));
// 自機と弾の距離が2以下なら衝突
if(distance < 2.0) {
is_shot = true;
}
}
// 弾との距離は十分大きいので衝突しない
console.log(is_shot ? "衝突した!": "衝突してない!");
// ユークリッド距離1の弾を作り衝突判定
let bullet_x = jiki.x;
let bullet_y = jiki.y + 1.0;
let new_bullet = {x: bullet_x, y: bullet_y};
bullets.push(new_bullet);
// 同じ判定をおこなって衝突するかどうか
is_shot = false;
for(let bullet of bullets){
//自機と弾のユークリッド距離を計算
let distance = Math.sqrt(Math.pow(bullet.x - jiki.x, 2) + Math.pow(bullet.y - jiki.y, 2));
// 自機と弾の距離が2以下なら衝突
if(distance < 2.0) {
is_shot = true;
}
}
// 衝突する
console.log(is_shot ? "衝突した!": "衝突してない!");
次に空間分割を使って衝突判定をしたものです。
let width = 800;
let height = 500;
// 画面の真ん中に自機がいる
let jiki = {x: width / 2.0, y: height / 2.0};
let bullets = [];
// 自機からマンハッタン距離2以上離れた場所に弾を100個設置
for(let i = 0; i <= 10; ++i){
for(let j = 0; j <= 10; ++j){
let margin = 14;
let x = i * (width - margin * 2) / 10 + margin;
let y = j * (height - margin * 2) / 10 + margin;
if(Math.abs(x - jiki.x) + Math.abs(y - jiki.y) < 4.0){
continue;
}
bullets.push({x: x, y: y});
}
}
// 空間分割用の3次元配列を作る
let split_num = 3;
let splited = new Array(split_num);
for(let i = 0; i < split_num; ++i){
splited[i] = new Array(split_num);
for(let j = 0; j < split_num; ++j){
splited[i][j] = [];
}
}
// 一つ前の処理で作った配列に弾を入れておく
let is_shot = false;
for(bullet of bullets){
let x_index = Math.floor(bullet.x / width * split_num);
let y_index = Math.floor(bullet.y / height * split_num);
splited[x_index][y_index].push(bullet);
}
// 弾との距離は20なので衝突しない
console.log(is_shot ? "衝突した!": "衝突してない!");
// ユークリッド距離1の弾を作り衝突判定
let bullet_x = jiki.x;
let bullet_y = jiki.y + 1.0;
let new_bullet = {x: bullet_x, y: bullet_y};
bullets.push(new_bullet);
let new_bix = Math.floor(bullet_x / width * split_num);
let new_biy = Math.floor(bullet_y / height * split_num);
splited[new_bix][new_biy].push(new_bullet);
// 同じように判定をする
is_shot = false;
for(bullet of bullets){
// 自機のいる場所を特定
let x_index = Math.floor(bullet.x / width * split_num);
let y_index = Math.floor(bullet.y / height * split_num);
// 自機の近くだけを判定
for(near_bullet of splited[x_index][y_index]){
let distance = Math.sqrt(Math.pow(near_bullet.x - jiki.x, 2) + Math.pow(near_bullet.y - jiki.y, 2));
if(distance < 2.0){
is_shot = true;
}
}
}
// 弾との距離は20なので衝突しない
console.log(is_shot ? "衝突した!": "衝突してない!");
ここでは半径2以内なら衝突という判定をしています。分割された長方形の大きさは幅$ 266.7 $ 高さ $ 188.9 $なので、半径より十分大きいので一つの長方形しか判定をしなくていいですね。自機がちょうど長方形の境目にいる場合は複数の長方形に対して判定しなければなりませんね。
4分木を使った空間分割
方法
先ほどの方法で縦16、横16個分割したものに対し、自機から半径r以内の弾を全部取り出すことを考えてみましょう。自機から半径rの円を書いてそれと重なった部分を持つ長方形だけを判定すればいいですね。全て長方形に対してこの円との共通部分を持っているかどうかの判定を行うと256通りになりますが、これをもっと減らす方法があります。それが4分木です。
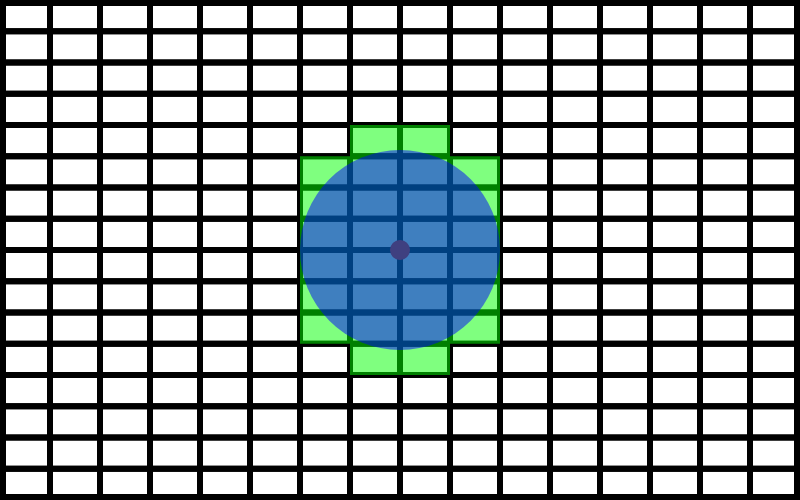
探索数が多い原因は分割された長方形の数が多いというところにあります。この長方形の数を減らせればいいわけですね。
ここで4つで一つの長方形として捉えられるという特徴に注目します。下の絵をみてください。赤い正方形が書かれてますね。この赤い部分には4つの長方形を含んでいますが、これは一つの長方形として捉えることができますね。
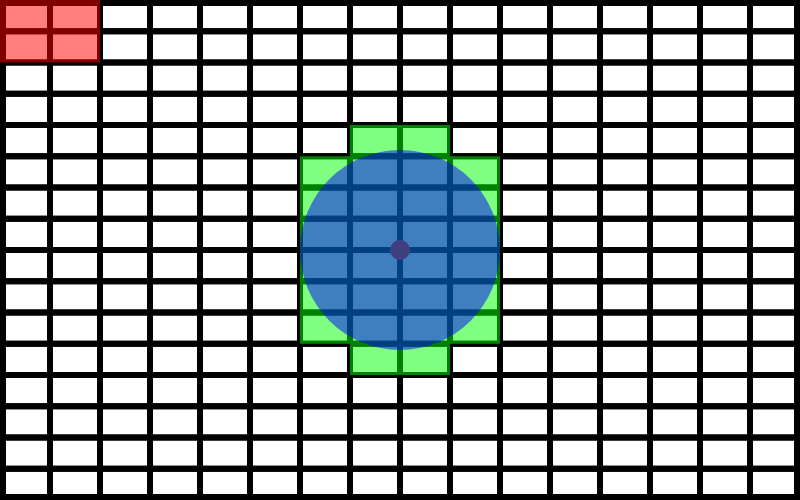
この4つの小さい長方形を一つの大きな長方形として捉えるという操作を全ての長方形に対して行ってみます。そうすると長方形の数が1/4に減りましたね。64個の長方形だけを調べれば良さそうです。
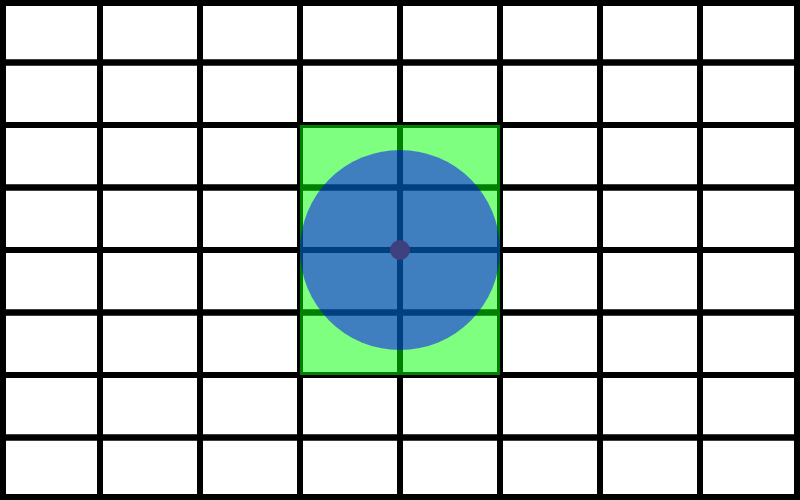
そして、緑の長方形だけがこの円と重なっているので、この緑の長方形を4分割してみましょう。そうすると円の中心だけ細かく探索できるようになりましたね。
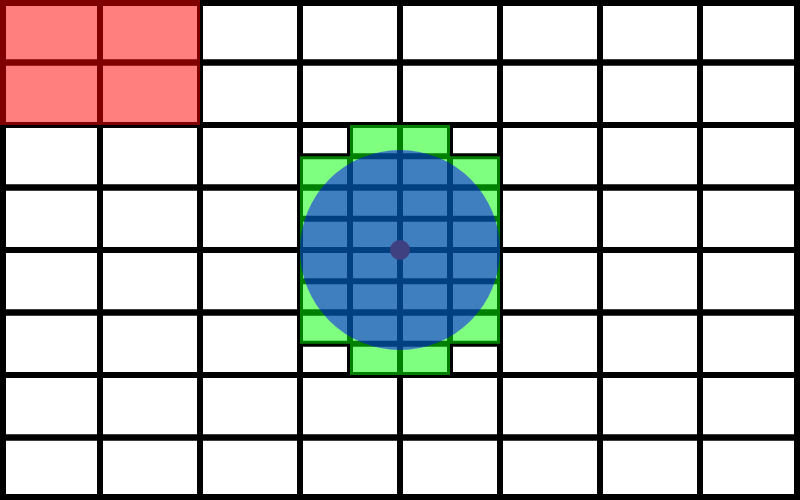
まだ探索数を減らせますね。というのはもう一度この赤い長方形の部分は大きな長方形として認識できるわけです。なので先ほどと同じようにやってみましょう。
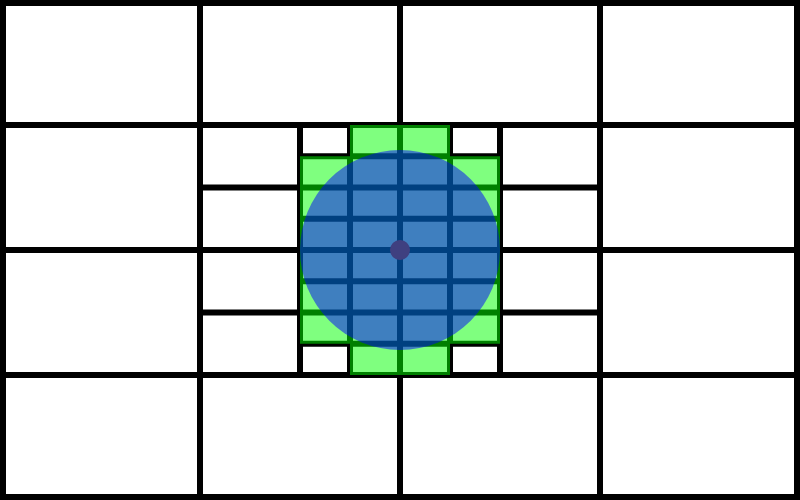
このように必要なときに必要な分だけ長方形を分割するのが4分木です。実際に探索する場合は画面全体を一つの大きな長方形として捉えて、円と長方形が共通部分を持つなら分割し、探索をする感じですね。そして、十分小さい長方形になったら、分割をやめてそこの長方形に含む球を探索します。2次元なので4分割にしましたが、3次元なら8分割します。
実装方法
実装するには円と長方形が共通部分を持っているかどうかを判定しなければなりません。これは頂点もしくは辺の一部が円の中にあるかどうかを判定すれば良さそうです。まずは頂点のことだけを考えてみましょう。各頂点と円の中心の距離をはかり、それが円の半径以下なら円の中にありますね。
次に頂点だけで考えた場合漏れるケースを考えてみましょう。下の絵のような場合は頂点は円の中にないですが、辺の一部は頂点の中にあるのでこれは探索しなければいけないです。この場合は円の中心から垂線を伸ばしてその長さを測ると辺と円の中心の距離になります。その距離が円の半径以下なら共通部分を含みますね。
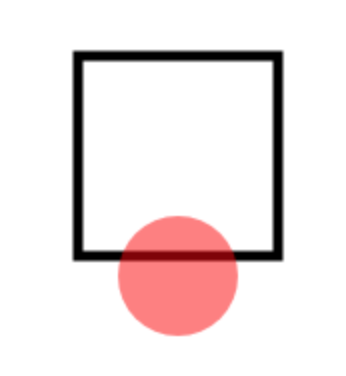
下の辺と共通部分を持つ場合、長方形の左上の頂点のx座標を$ x_1 $、右上の頂点のx座標は$ x_2 $とした場合、円の中心の$ x $座標が$ x_1 $と$ x_2 $の間にあります。上の辺の場合も同じですね。左右の辺の場合もy座標に対して同じことをすればいいです。
あと木構造を扱うので再帰的な判定を行います。人によってはそこがボトルネックになったりします。
サンプルコード
const WIDTH = 800;
const HEIGHT = 500;
// 画面の真ん中に時期がいる
let jiki = {x: WIDTH / 2.0, y: HEIGHT / 2.0};
let bullets = [];
let sum = 0;
// 自機からマンハッタン距離2以上離れた場所に弾を100個設置
for(let i = 0; i <= 100; ++i){
for(let j = 0; j <= 100; ++j){
let margin = 14;
let x = i * (WIDTH - margin * 2) / 100 + margin;
let y = j * (HEIGHT - margin * 2) / 100 + margin;
if(Math.abs(x - jiki.x) + Math.abs(y - jiki.y) < 4.0){
continue;
}
bullets.push({x: x, y: y});
}
}
//長方形クラス
class Rectangle{
constructor(x, y, width, height){
this.x = x;
this.y = y;
this.width = width;
this.height = height;
}
point_dist(point){
let within_x = this.x < point.x && point.x < this.x + this.width;
let within_y = this.y < point.y && point.y < this.y + this.height;
// 自機が長方形の中なら距離は0
if(within_x && within_y){
return 0;
// 上下の辺が一番近い場合
}else if(within_x){
return Math.min(Math.abs(point.y - this.y), Math.abs(point.y - this.y - this.width));
// 左右の辺が一番近い場合
}else if(within_y){
return Math.min(Math.abs(point.x - this.x), Math.abs(point.x - this.x - this.height));
}
// それ以外は頂点が一番近いので頂点の中から一番近いものを探す
return Math.min(
Math.sqrt(Math.pow(point.x - this.x, 2) + Math.pow(point.y - this.y, 2)),
Math.sqrt(Math.pow(point.x - this.x, 2) + Math.pow(point.y - this.y - this.height, 2)),
Math.sqrt(Math.pow(point.x - this.x - this.width, 2) + Math.pow(point.y - this.y, 2)),
Math.sqrt(Math.pow(point.x - this.x - this.width, 2) + Math.pow(point.y - this.y - this.height, 2)),
);
}
}
class Tree{
constructor(rect){
this.rect = rect;
// 横幅が小さくなったら終わり
if(rect.width > 50){
// 子ノードの数は4つ
this.trees = new Array(4);
// 子ノードの大きさは 1/ 2
const child_width = this.rect.width / 2;
const child_height = this.rect.height / 2;
for(let i = 0; i < 4; ++i){
// 左上 -> 右上 -> 左下 -> 右下の順番で追加
let x = this.rect.x + (i % 2) * child_width;
let y = this.rect.y + Math.floor(i / 2) * child_height;
this.trees[i] = new Tree(new Rectangle(x, y, child_width, child_height));
}
}else{
this.bullets = [];
}
}
// 木構造に弾を挿入してみる
insert(bullet){
// 子ノードを持たない時
if(this.bullets !== undefined){
sum++;
this.bullets.push(bullet);
return this;
}
for(tree of this.trees){
if(tree.rect.point_dist(bullet) <= 0){
tree.insert(bullet);
break;
}
}
return this;
}
// 自機の近くにある球を全て取得する
near_bullets(radius){
// 自機と長方形の距離が半径以上の時はからの配列を渡す
if(this.rect.point_dist(jiki) > radius){
return [];
}
// 子ノードを持たない時
if(this.bullets !== undefined){
let ret = [];
for(bullet of this.bullets){
// 距離が近いものだけを選択する
let dist = Math.sqrt(Math.pow(bullet.x - jiki.x, 2) + Math.sqrt(Math.pow(bullet.y - jiki.y, 2)));
if(dist < radius){
ret.push(bullet);
}
}
return ret;
// 子ノードを持つ場合
}else{
let ret = [];
for(tree of this.trees){
if(tree.rect.point_dist(jiki) < radius){
ret = ret.concat(tree.near_bullets(radius));
}
}
return ret;
}
}
}
let tree = new Tree(new Rectangle(0, 0, WIDTH, HEIGHT));
for(bullet of bullets){
tree = tree.insert(bullet);
}
// 半径10以内にある球を全部取得
console.log(tree.near_bullets(10));