オイラー法入門

オイラー法とは

オイラー法はコンピューター上でで常微分方程式を解くための手法です。
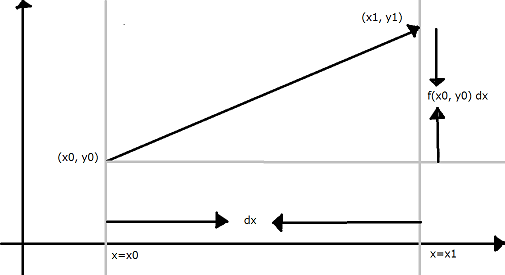
では、具体的にどういう風に常微分方程式を解くのでしょうか？まず、$ \frac{dy}{dx} = f(x, y) $の形にします。まず、初期値$ (x_0, y_0) $を設定します。次の漸化式を使って逐次的に$ (x_n, y_n) $を求めていきます。

\left\{
    \begin{array}{l}
        x_{n+1} = x_n + dx \\
        y_{n+1} = y_n + f(x_n, y_n) dx 
     \end{array}
\right.

これが、オイラー法です。

ソースコードと実行結果

ソースコード

$ \frac{dy}{dx} = 2 x $の解を求めるプログラムです。出力結果をCSVにして保存できるようにしてあります。

euler.c

#include <stdio.h>
#include <math.h>

#define EPS (__builtin_pow(2.0, __builtin_floor(__builtin_log2(1.0e-6))))
#define f(x,y) (2*( x))

int main(){
    double x = 0, y = 0;
    while(x < 2){
        printf("%f, %f \n", x, y);
        y += f(x, y) * EPS;
        x += EPS;
    }
}

実行結果

このプログラムの実行結果は$ y = x ^ 2 $に近い値が得られるはずです。このプログラムの実行結果をCSVにしてグラフにしてみました