C言語で学ぶ台形公式による積分の近似

台形公式とは

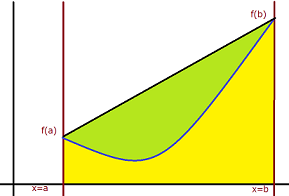
下の絵の青い線がが積分したい関数のグラフ、aからbまでを積分したい範囲(左の茶色の線から右茶色の線）だと思ってください。台形公式とは緑と黄色の部分の面積を積分した値だと考えることです。その値は

 \frac{(f(a) + f(b)) (b - a)}{2} 

になりますね

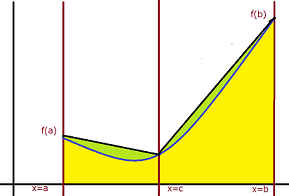
しかし、図で見て分かる通り緑の部分が明らかに余計です。なので、$ a $と$ b $の間に$ c = \frac{a + b}{2} $という点を設けましょう。緑色と黄色の部分の面積の合計は

\frac{(f(a) + f(c)) (c - a) + (f(c) + f(b)) (b - c)}{ 2 }

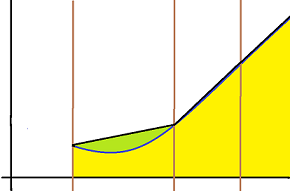
になりますね。するとついさっきの図より緑色の部分が減っているのがわかります。これが台形公式です。$ a $と$ b $の間に点があればあるほど、その値は正確になります。
!　

ソースコード

integral.c

# include <stdio.h>
# include <math.h>

# define EPS (1.0e-6)
# define f(x) ((x)*(x))

int main(){
    double a = 0, b = 2, sum = 0;
    for(double x = a; x < b; x += EPS){
        sum += (f(x) + f(x+EPS));
    }
    sum *= (EPS / 2);

    printf("%f\n", sum);
}