関数型言語でよく使われるReduce処理の活用事例です。これまでどんな時に使うとスマートなのかわからなかったのですが、複利計算なんかでばっちり使え、イメージがつかめたので紹介します。
基本的な使い方なので、いまいち使いどころがつかめない人向けです。
※以下はR言語の例ですがいろいろな言語で使われる考え方です。
Reduceとは
Reduce関数とは…
隣り合う 2 つの要素に対して(左から右へ)同時に関数を適用し、単一の値にします。
なるほど、わからん。
例えば、以下のような配列(ベクトル)があった場合
> data<-c(1,2,5,7)
> data
[1] 1 2 5 7
要素を左から順に取り出して処理、を繰り返して、最終的に1つの値にするみたいです。
例えばこう書いた場合
> Reduce(function(a,b){a+b},data)
- data[1]とdata[2]が関数の引数a,bに入ります
- a+b ("1"+"2")が実行されます
- ↑の結果の"3"とdata[3]が関数の引数a,bに入ります
- a+b("3"+"5")が実行されます
- ↑の結果の"8"とdata[4]が関数の引数a,bに入ります
- a+b("8"+"7")が実行され、15が答えとして出てきます
なお、R言語の場合は引数にaccumulate=TRUEを入れると途中経過が見れます。
> Reduce(function(a,b){a+b},data,accumulate = T)
[1] 1 3 8 15
半分だけ理解できる例
なかなか使いどころがわからず、いろいろ調べているとこんな例がありました。
Reduceで最小値を見つける!
> Reduce(function(a,b){ifelse(a<b,a,b)},data)
[1] 1
>#こっちでいい
> min(data)
[1] 1
Reduceを使うと、小さい方を選ぶだけで最小値が見つかるよ!という例です。
いや、min()でいいじゃんとツッコミましたが、1つずつ値を比較していくという動きはわかります。ただ、順番に結果を受け渡していくメリットがイメージしにくいです。
と、もやもやしているとちょうどいい例を発見しました。
複利計算してみよう
複利とは、預金などで元本に対して利息が発生した場合、元本+利息を次の元本に組み入れるものです。
100万円預けて、年5%(値は適当です)の利息が付く場合。
100 → 105 → 110.25 → 1115.76 → 121.55
と年々増え方が徐々に大きくなっていきます。
では20年後にどうなっているか、を計算してみます。
> 利息<-c(1.05,1.05,1.05,1.05,1.05,1.05,1.05,1.05,1.05,1.05,
> 1.05,1.05,1.05,1.05,1.05,1.05,1.05,1.05,1.05,1.05)
> Reduce(function(a,b){a * b},init=100,利息,accumulate = T)
>
[1] 100.0000 105.0000 110.2500 115.7625 121.5506 127.6282 134.0096
[8] 140.7100 147.7455 155.1328 162.8895 171.0339 179.5856 188.5649
[15] 197.9932 207.8928 218.2875 229.2018 240.6619 252.6950 265.3298
# 途中で利息が変わっても大丈夫
> 利息<-c(1.05,1.05,1.05,1.05,1.05,1.05,1.05,1.04,1.04,1.04,
> 1.03,1.03,1.02,1.02,1.01,1.01,1.01,1.01,1.01,1.01)
> Reduce(function(a,b){a * b},init=100,利息)
[1] 185.4506
年利配列を作り、初期値に100を設定。順に年利をかけていくと推移が計算できます。
おまけ:シミュレーションがしたかった
上の例では単に利息を計算するだけですが、年利がガンガン変わっていくような投資をした場合、数年後に得られる収益のシミュレーションというのを考えていました。
個別に名前は出しませんが、ぱっと目についた投資信託商品で
- 平均年利が4.07%
- 年利のばらつき(標準偏差)が13%
- 年ごとの手数料が1.3%
というものがありました。
年利は定期預金なんかに比べるとかなり高いです、しかし年により当然ばらつきがあるので損するときもあるはずです。
この商品を20年運用した場合、果たしてどのぐらいお金が増えるのか、シミュレーションしてみましょう。
初期資金100万円、さらに毎年20万追加するような場合を考えてみます。
年利は標準偏差13%をベースにランダムに変えます。
それを10000回試してみて、収益がどうなるでしょうか。
年利<-1.04075
標準偏差<-0.1318
初期資金<-100
信託報酬<-0.0135
追加<-20
年数<-20
# 試行回数
sample<-10000
# 計算用ベクトル
data<-c(初期資金,seq(1,1,length=年数)*追加)
# 結果保持用
ret<-data.frame(rep(0,times=sample))
# 複利計算をsample回繰り返して保持する
ret<-apply(ret,1,function(v){
Reduce(function(a,b){
return((a*(年利+rnorm(1)*標準偏差)+b)*(1-信託報酬))
},data)
})
# 損益に換算
ret2 <- ret - sum(data)
# ヒストグラム
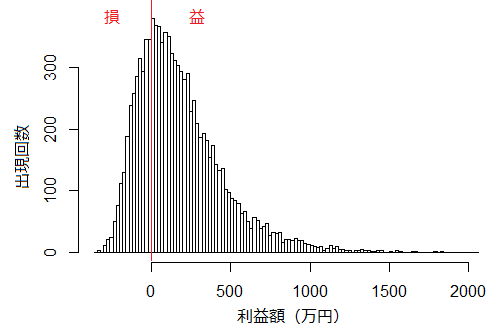
h<-hist(ret2,breaks = 100)
# 黒字率
sum(ret2>0)*(100/sample)
# [1] 73
# 合計投資額
sum(data)
# [1] 500
summary(ret2)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# -343.70 -12.06 128.50 183.00 316.50 2055.00
中央値は+128.5万なので期待できそうです。
しかし、年利4%でもばらつきが多いため、20年後に黒字になる確率は73%程度になってしまうようです。
もちろん、本当に投資シミュレーションしようと思うともっと考慮する要素はあると思いますが、大雑把にでもさくっと計算できるのはプログラマーの特権(?)ですね。
あと、計算~グラフ化・集計までささっとできるR言語は結構便利です。