本記事の内容
おもしろい,興味深い,ためになる,教養としてしっておくとよい,確率と統計学に関する話を書きました。確率,統計学の知識があまりない人が,それらに興味を持つきっかけになるような教科書というような位置づけです。統計学を少しだけ学んだという人向けのすこし詳しい話(詳細話)もありますのでそういう人も是非読んでみてください。
注意事項
記事内容の正確性は保証できません。理由は①私が趣味で書いているだけだから。②正確さよりも分かりやすさを重視しているから。の2点です。ただし,当然ですがもちろん可能な限り正確には書いていきます。
また,「教科書」の位置づけと言いましたが,これを読んだからと言って基礎が身につくわけではないのでご了承ください。
目次
第1章 平均の落とし穴(平均値,中央値,最頻値)
・・・・具体例(年収の分布)
・・・・平均が機能しない理由
・・・・中央値,最頻値
・・・・詳細話(刈り込み平均)
・・・・まとめ
第2章 相関に惑わされるな(擬相関,偏相関,相関と因果)
・・・・相関とは
・・・・擬相関の例(アイスと溺死)
・・・・擬相関が発生する理由
・・・・血圧と年収の関係
・・・・相関と因果の違い(ピアノの例)
・・・・詳細話(偏相関)
・・・・補足話(擬相関の定義)
・・・・まとめ
第3章 全体と部分で結果が違う(シンプソンのパラドックス)
・・・・シンプソンのパラドックス(テストの平均点)
・・・・シンプソンのパラドックス(仕事の現場では)
・・・・まとめ
補足章 参考文献等
章は随時追加予定です。
今後追加予定の章(2022.02.23現在)
第4章 その介入には本当に効果はあるのか(平均への回帰)
第5章 その検査,本当に有効?(条件付き確率)
第1章 平均の落とし穴
私たちはしばしば平均を基準として物事の良し悪しを判断します。たとえば,「テストで平均点以下をとってしまったからダメだなあ」とか「平均体重より重い,もっと痩せなきゃ」といったようなことです。このような判断を下すのは,私たちの中に「平均=ふつう」という認識が暗に存在するためです。平均(=ふつう)以下だから悪い,平均(=ふつう)以上だから良い,というようにです。
しかし,いま一度よく考えてみてください。
「平均=ふつう」という認識は本当に正しいのでしょうか?
実は,「平均=ふつう」という認識は必ずしも正しくはないのです。その具体例を以下で紹介していきます。
具体例(年収の分布)
下の図は,平成21年の所得(=年収)の分布を描いたものです。横軸が年収,縦軸が割合です。この図からは年収の平均が547万5000円であることが読み取れます。また,平均年収以下の人が61.3%いることも分かります。
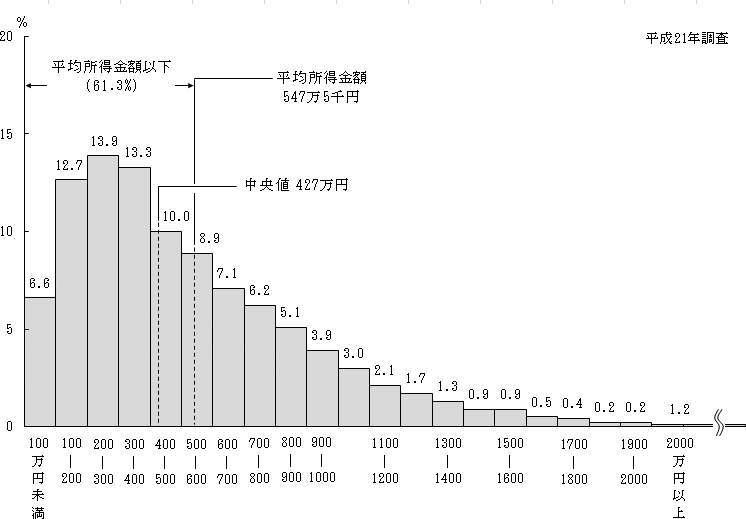
引用:厚生労働省 平成21年
もう一度言います。**61.3%の人が平均年収以下なんです。**逆に言えば,平均よりも多く稼いでいる人は約39%しかいないのです。これでも,「平均=ふつう」であると言えますか?
想像よりも,平均年収を超えるというハードルが高いと思った人が多いのではないでしょうか。上位39%の人しか平均を超えることができないのです。
この例のように,「平均=ふつう」が必ず成り立つとは限らないのです。この平均年収の例は,「平均=ふつう」が上手く機能してないもっともよい例です。こういう場合は平均を判断基準にすると,判断を誤る可能性があるので気をつけなければなりません。
平均が機能しない理由
平均が機能しないのには理由があります。それは外れ値が影響しているからです。外れ値とは極端に大きい値,または極端に小さい値をとるデータのことを指します。年収の例で言えば,年収1000万や年収1億といった人たちのことです。
年収数千万,何億というデータはごくわずかですが存在します。しかし,それらのデータのスケール(規模感)が他の人たちのデータとあまりにも異なります。平均はその計算式上,外れ値の影響を強く受けます。年収が極端に高い人が少しいるせいで,平均の計算結果が上方に吊り上がってしまうのです。
中央値,最頻値
上では平均が上手く機能していない例を見てみました。しかしそうはいってもやはり,私たちは何らかの基準を持ちたいと考えてしまいます。基準を持たないと良しあしを判断できず,不安になってしまうからです。
このように,平均が上手く機能していない,でも何らかの基準が欲しい。そういう時に頼りになるのが,この節で紹介する中央値と最頻値です。
中央値とは,データを小さい順に並べたときの小さい方から数えて丁度真ん中のデータのことです。
最頻値とは,最も頻繁に現れるデータのことです。俗っぽく言えば,
中央値とは,世間のちょうど真ん中に位置する人
最頻値とは,世間の大多数の人 のことです。
前の図で言うと,中央値は427万円,最頻値は200~300万円です。言い換えれば,427万円稼げばちょうど上位50%,200~300万円稼ぐ人の割合が一番多い,ということです。
平均が機能していないときは,**中央値や最頻値の方がきちんと世間の実情を反映していることが多いです。とくに,最頻値なんかは一番イメージがしやすいのではないでしょうか。「最頻値=世間一般」**とイメージできるからです。
したがって,平均が機能していないときは,**平均よりも中央値,最頻値にも目を向ける必要があります。**さらに言えば,これらの値だけを見るのではなく,上の図のように,分布全体を把握するのが一番よいです。
詳細話(刈り込み平均)
平均以外に,中央値,最頻値にも目を向けることが大切だと前述しましたが,では,そのとき平均は役に立たないのかと言うとそうではありません。
平均の欠点は外れ値の影響を強く受けるという点でした。この欠点を改良したのが**刈り込み平均(トリム平均)**です。刈り込み平均は以下のような数式で表されます。
$n$個のデータ$x_1, x_2, ..., x_n$に対して,これらのデータを小さい順に並べ替えたデータをそれぞれ$x_{(1)}, x_{(2)}, ..., x_{(n)}$とする。このとき刈り込み平均$\bar{x_{t_{k}}}$は以下のようになる($k$は自分で設定する整数。ここでは例として$k=3$とする)。
\bar{x_{t_3}} = \frac{x_{(4)}+x_{(5)}+ ... + x_{(n-4)}+x_{(n-3)}}{n-2\times3}
つまり,小さい順に並べ替えたデータのうち,**小さい方からk個と大きい方からk個を除外したデータで平均を計算するということになります。この操作によって,極端に小さいデータや極端に大きいデータを除外できるので外れ値の影響を減らすことができます。**こういった平均もあるんです。
まとめ
平均は必ずしも普通を意味しない!!
中央値や最頻値も確認しましょう!!
第2章 相関に惑わされるな
相関という言葉はほとんどの人が聞いたことがあると思います。相関係数という数学・統計学用語から来ています。しかし,この相関という言葉を使うときにはいくつかの注意すべき点があります。相関というのは広く知られている語であるのに,その注意点はほとんど知られていないことが多いんです。
相関と言う言葉をなんとなくでしか知らない人,注意点を知らない人は,悪意のある人に騙されてしまう可能性があります。ビジネスマンであれば,相関に対して間違った解釈をしてしまった結果,開発商品の売り上げが伸びない,施策の効果が出ないといった事態になります。
こういった事態を防ぐために,相関についての注意点,正しい知識をぜひ身に付けてください。相関についての注意点で今回紹介するのは,以下の2つです。
① 擬相関に騙されるな
② 相関と因果を混同しない
相関とは
相関という語のもと,相関係数とはまず,2つの事柄のあいだの関係を表す用語です。2つの事柄の間に,一方の値が大きいとき,他方の値も大きいという関係がある(言い換えれば,一方の値が小さいとき,他方の値も小さい)とき,正の相関があると言います。
文章より図を見た方が早いですね。下の図は正の相関をもつデータの一例です。
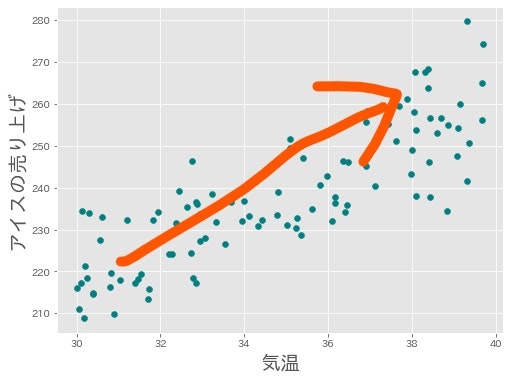
この図は,ある夏100日分の,気温とその日のアイス屋さんのアイスの売り上げ個数をプロットした散布図です。気温が高い日はアイスの売り上げ個数も多いので正の相関があります。このように,正の相関は散布図上では右上がりの傾向として現れます。
暑い日ほど,アイスが良く売れるということが読み取れます。これは,暑いときは涼を求めてアイスが食べたくなるという状況の現れであることが直感的に理解してもらえると思います。
次は負の相関の例です。
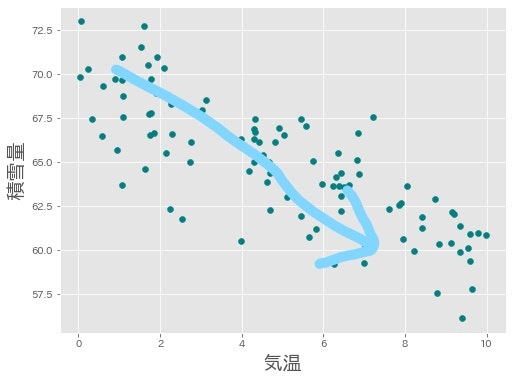
負の相関とは正の相関とは逆で,一方が大きいとき,他方が小さいと言う関係を指します。この散布図は,ある冬100日分の気温と積雪量を描いたものです。気温が低い日ほど,積雪量が多いということが読み取れます。これも,確かにそうですね。
負の相関は散布図には右下がりの傾向として現れます。
擬相関の例(アイスと溺死)
上では,正の相関,負の相関の例を1つずつ見てきました。次の散布図はどうでしょうか。
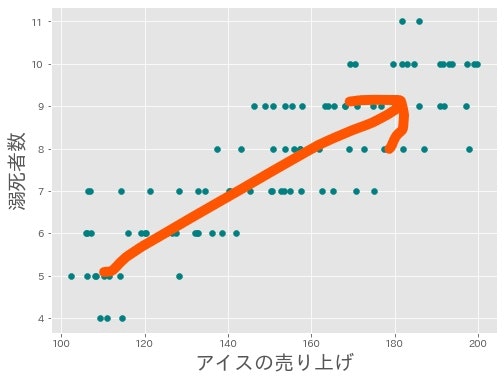
これは夏の100日分のアイスの売り上げ個数とその日の溺死者数をプロットした散布図です。**正の相関があります。**この図からは,
アイスの売り上げが多い日は溺死者数も多いことが分かります。
そんなことあるんでしょうか?**アイスが売れる日は人が良く死ぬ?アイスを売れば売るほど,溺死者が増える?おかしいと思いますよね?**そんなわけないと。じつは,そんなことあるんです!!
とはいっても,
本来的にはアイスの売り上げと溺死者数の間には関連はありません。
なのに,相関がある。
このように,本来は関係がないのに,いかにも相関が存在するように見えることを擬相関があるといいます。擬相関は,擬似相関,見かけの相関,見せかけの相関,偽相関とも言います。その名の通り,見かけ上の相関を指します。
**擬相関が存在すると,本来は関係のない2つの事柄の間にあたかも関連があるように見えてしまうので注意が必要です。**ここからは,擬相関が発生する理由について見ていきます。
擬相関が発生する理由
2つの事柄の間に擬相関が発生する理由は,その背後に2つの事柄に共通な別の要因が存在するからです。下図を見ると分かりやすいと思います。
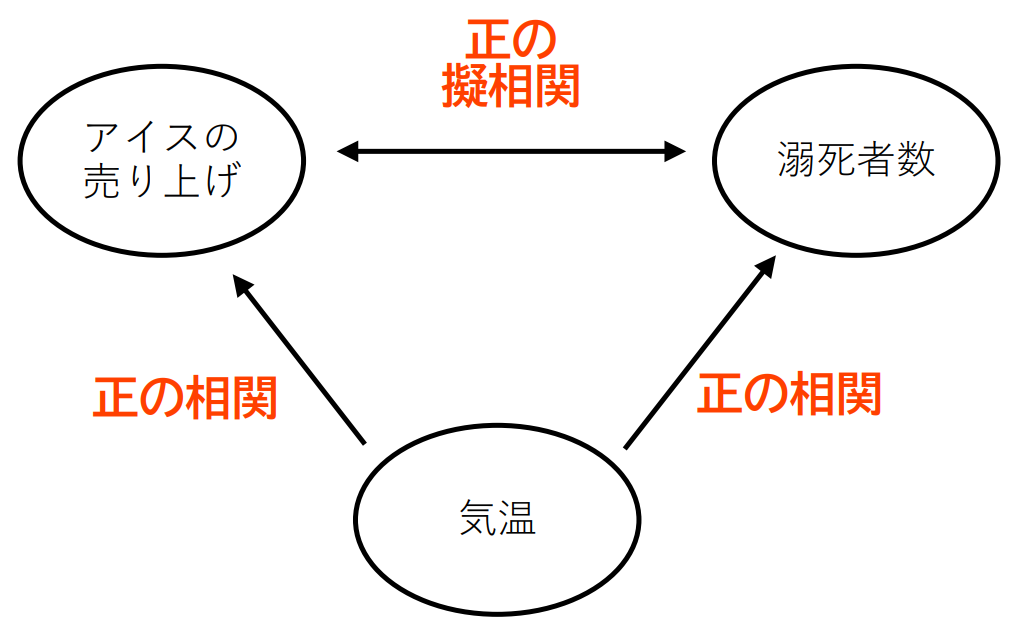
気温が高い日は,アイスが良く売れる。
気温が高い日は,溺死者が増える(水辺に遊びに行くので)。
→アイスの売り上げも溺死者も同時に増える
→正の相関が現れる(疑相関)
上の図のような関係が存在するとき,擬相関が発生します。しかし,あらためて言いますが,**擬相関は見かけ上存在するだけで,実際には2つの事柄の間に関連はないのです。**この点に注意してください。
血圧と年収の関係
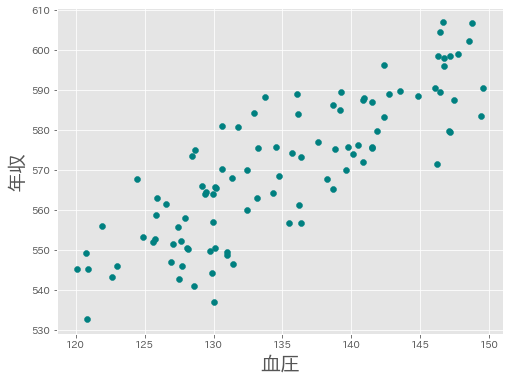
次の図は血圧と年収の散布図です。さて,この図からどのような傾向が読み取れるでしょうか,続きを読み進める前に考えてみてください。
.
.
.
.
.
.
.
.
.
上の図から読み取れるのは,血圧が高い人ほど年収が高いという傾向です。さて,この傾向をもとに,**「もっといっぱい稼ぐために血圧上げるぞ~!」**とあなたは考えますか?そう考える人はすこし早とちりです。
実は,血圧と年収の間にも擬相関が存在しています。つまり,本来は血圧と年収の間に関連はないのです。血圧を上げたところで年収は上がりません。もっと稼ぎたかったら,仕事を頑張りましょう。
さて,血圧と年収の背後で擬相関を引き起こしている要因は何か分かりますか?下にある答えを見る前に少し考えてみてください。
.
.
.
.
.
.
.
.
.
.
正解は年齢です。
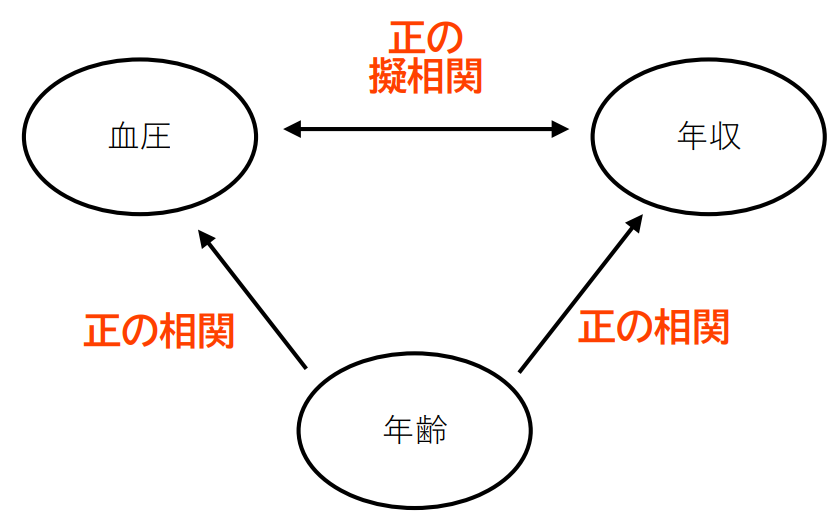
年齢が高い人は生活習慣が乱れてきてることが多いので高血圧になる傾向があります。そして,日本はまだ年功序列の傾向があるので,年齢が高い人ほど年収は高いです。
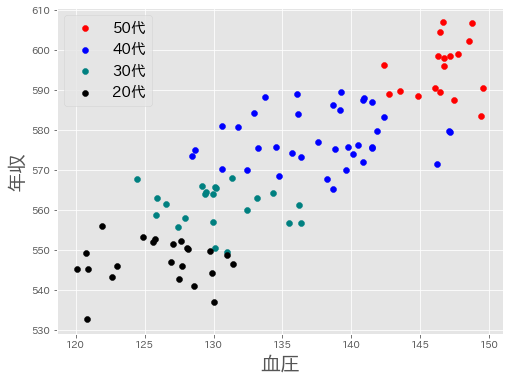
これらが合わさって,血圧が高い人ほど年収が高いという見かけの関係が見えてしまうのです。実際,年代別に見てみると,下図のようになり,血圧と年収にはほとんど関連が無い,または逆にほんのすこし負の相関(右下がりの傾向)があることがわかるでしょう。
相関と因果の違い(ピアノの例)
これまでに,相関,擬相関がある例をたくさん見てきました。また,新しい例を見てみましょう。それは,ピアノを習っていたことがある大学生を対象にしたアンケート調査の結果を散布図にまとめたもので,ピアノを習っていた年数とその人の偏差値を描いたものになっています。これも少し正の相関があることが見てわかります。
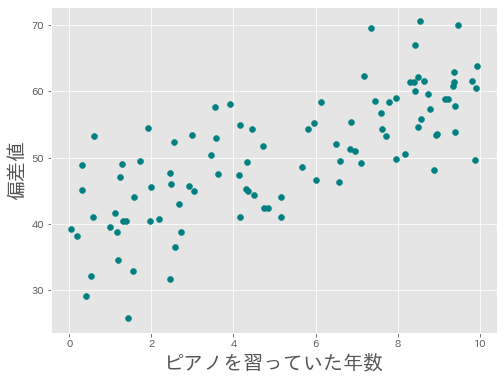
この散布図からは**「ピアノを習っていた年数が長い人は偏差値も高い」と言う傾向が見て取れます。もちろん逆も言えます。つまり偏差値が高い人はピアノを習っていた年数が長い**ということです。
ではここからさらに一歩進んで,**「ピアノを長く習うと偏差値が高くなる」と言えるでしょうか。つい先ほど述べた,「ピアノを習っていた年数が長い人は偏差値も高い」**とは少し違うことに注意してください。
どうでしょうか?ピアノを長く習うと偏差値が高くなる(=賢くなる)でしょうか?たまに聞きますよね,子どもに早いうちからピアノを習わせておくと言い,賢くなるからと。これは正しいのでしょうか。結論を言うと,正しいかどうか,上の散布図だけでは分からない,となります。
その理由は「ピアノを習っていた年数が長い人は偏差値も高い」は相関を言っているのに対して,「ピアノを長く習うと偏差値が高くなる」は因果について述べているからです。
因果関係とは,片方の事柄を操作する(=変化させる)と,それにつれてもう一方の事柄も変化するという関係のことを言います。相関との違いは因果には向きがあると言うことです。
【相関と因果の違い】
相関:相互的な関係,向きは存在しない。
因果:一方向な関係,向きが存在する。
【相関と因果の具体例】
①
相関:気温が高い日は,アイスが良く売れる
因果:気温を高めれば,アイスが良く売れる
②
相関:アイスが良く売れる日は,溺死者も多い
因果:アイスをたくさん売れば,溺死者を増やせる
③
相関:血圧が高い人は,年収も高い
因果:血圧を高めれば,年収が高まる
④
相関:ピアノを習った年数が長いと偏差値も高い
因果:ピアノを長く習うと,偏差値が高くなる
というように,相関と因果は似ているようで全く違うことを言っています。
そして,大事なことがもうひとつあります。それは,
相関があるからと言って必ずしも因果が存在するとは限らない
ということです。
このことはなんとなく理解していただけると思います。すぐ上の4つの具体例では全て相関が存在します(ここでは擬相関も含めて話します)。しかし,②と③には因果は確実に存在しません。だって,アイスを頑張ってたくさん売ったからと言って溺死する人が増えるわけないですから。だって,血圧をグングン高めて高血圧症になったからといって,もらえるお金が増えるわけないですから。
このように,**相関が存在するからと言って因果が存在するとは限りません。**このことは最重要な注意点ですので,よく知っておいてください。
相関があっても因果が存在するとは限らない,ということを知っていれば,「ピアノを長く習うと偏差値が高くなる」と必ずしも言えないということに納得できると思います。散布図からはこのような因果の存在は言い切れないのです。相関はあるのに!です。
でもなぜか,上の図だけを見て,子供にピアノをいっぱい習わせよう!そしたら将来賢くなるから!と考える人が一定数いるんですよね,,,しかし,それは仕方ないことで,このような因果は頭の中で簡単に想像できてしまうからなんです。
例えば,「ピアノ年数と偏差値に相関がある」→「偏差値を高めればピアノを習っていた年数がふえる」とはだれも考えないですよね?相関には向きは存在しないので別にこのように考えることも可能ではあるのに,です。
でも「ピアノ年数と偏差値に相関がある」→「ピアノをたくさん習えば偏差値が高くなる」となったとたん,正しそうに見えてしまいます。しかし,相関から因果は言えないので,この説は正しいとは限らないのです(もちろん,正しい可能性もあります)。
もう一度言います。
相関があるからと言って必ずしも因果が存在するとは限らない
です。**じゃあ,因果が存在するかどうかはどうやって確認するの?**と思う人がいるかもしれません。相関は散布図書けば見た目ですぐ判断できたよね?因果はどうやって?
実は,因果関係が存在することを示すのはとても難しいことなのです。なので,因果があるかは簡単には分かりません。(実際に,2022年現在でも因果推論は未だに統計学界隈ではホットな話題です。)
したがって,大事なのは,因果があるとすぐに思い込まない。よくよく考えるということです。
【付け足し】
ピアノ年数と偏差値の関係については,見た目では相関がありますが,**これは擬相関だと考えられます。ピアノ年数と偏差値の背後に,「親の教育熱心度」**という共通の要因があるのでしょう。親が教育熱心だといろいろな習い事を子供にさせるでしょう,その中にピアノの習い事もあると思います。そして,勉強もいっぱいさせるでしょう,家庭教師をつけたり,塾に行かせたり。
その結果,ピアノ年数と賢さは同時に高まるので,相関があるように見える(と思います)。この要因によって,擬相関が引き起こされているだけで,ピアノを長く習わせても賢くなるとは言えない(と私は考えます。)
他にも,相関があるけど,因果は無い(というか分からない)と言う例はいっぱいあると思ので,皆さんも良かったら探してみてください,そして因果は存在するか考えてみてください。
詳細話(偏相関)
擬相関に騙されないようにしましょうと言いましたが,それが**本当の相関か,擬相関かはどのように見分けるのでしょうか。**それには,偏相関という指標を使います。
偏相関とは背後の要因の影響を除外した相関のことで,以下のような式で計算されます。
\rho_{X_1X_2|Z} = \frac{\rho_{X_1X_2} - \rho_{X_1Z}\rho_{X_2Z}}{\sqrt{1-\rho_{X_1Z}^2}\sqrt{1-\rho_{X_2Z}^2}}
$\rho_{X_1X_2|Z} = X_1$と$X_2$の$Z$の影響を除いた偏相関
$\rho_{X_1X_2} = X_1$と$X_2$の相関係数
$\rho_{X_1Z} = X_1$と$Z$の相関係数
$\rho_{X_2Z} = X_2$と$Z$の相関係数
血圧と年収の例で偏相関を計算してみましょう。
各相関係数を以下のように想定します。
$\rho_{血圧,年収} = 0.77$(散布図をみるにだいたいこれくらい)
$\rho_{血圧,年齢} = 0.85$(年齢が高い人ほど血圧高いという事実より,これくらい)
$\rho_{年収,年齢} = 0.91$(年齢高い人ほど年収多いという事実より,これくらい)
この時の,年齢の影響を除いた偏相関$\rho_{血圧,年収|年齢}$は,
\begin{eqnarray}
\rho_{血圧,年収|年齢} &=& \frac{\rho_{血圧,年収} - \rho_{血圧,年齢}\rho_{年収,年齢}}{\sqrt{1-\rho_{血圧,年齢}^2}\sqrt{1-\rho_{年収,年齢}^2}} \\
&=& \frac{0.77 - 0.85 \times 0.91}{\sqrt{1-0.85^2}\sqrt{1-0.91^2}} \\
&\simeq& -0.016
\end{eqnarray}
となります。$-0.016$はほとんどゼロなので,やはり血圧と年収の間にはほとんど関連が無いことが示されました。(まあ,設定した相関係数は根拠があるわけではなくだいたいなので真相はわかりませんけどね。もし興味を持った方いたら,実際にデータを集めて調査してみてください。)
補足話(擬相関の定義)
擬相関(擬似相関,Spurious Correlations)の意味をインターネットで検索してみた結果,「因果があるように見えるけれど,(それは第3の変数の影響を受けているからで)本来は因果がない」という定義が一番多かったです。一方で「本当は関連(相関)が無いのに,第3の変数のせいで相関があるように見える」という定義もちらほら見られました。この記事では擬相関を後者の意味で捉え,紹介しました。
前者の定義はwikipedia(とwikiが紹介している参考文献)やデータ分析関連の事業を行っている会社の記事,個人的な解説記事などで見られました。後者の定義は日本統計学会の公式Twitter,統計検定2級に準拠した解説記事を掲載しているサイトBellCurveの統計WEB,岩波データサイエンスvol.3の因果推論についての記事などで見られました。
擬相関と言う言葉を最初に定義した論文が見られればそれに倣うのですが,見つけられませんでした。私の主観ですが,本来的な意味は前者,のちに後者の意味も広まったんじゃないかなと思います。
前者が本来の意味であれば,この記事で紹介した擬相関の話はそれすなわち相関は因果を意味しないの話にまるっと包含されるので,話を2つに分けるのは適切ではないと思われるのですが,なんとなく私の個人的な好みで擬相関を後者の意味で捉えて,そして話を2つに分けました。
なんで後者が好みかと言うと,理由はいくつかあって。①"擬似"相関,"見せかけの"相関と言うワードは,「因果に見せかけた相関」というよりは,「相関自体が擬似,見せかけ」という捉え方の方が自然っぽいから。②もし前者の定義を擬相関と呼ぶなら,「本当は相関がないのに相関があるように見える」という現象には名前が無いことになる。ここで,偏相関という指標は第3の変数の影響を除いた相関係数を表すけど,これはどう見ても「本当は相関がないのに,相関があるように見える現象」用の指標で,こういう現象が良くあるからこそ偏相関の指標もあるわけで,この現象に名前が無いのはおかしいと思うから。③よくよく考えてみたんですが,相関があれば因果があるのは"本当であれば"当たり前なはずなんですよね。だって,2つの事柄の値が同時に増える(逆に同時に減る)=正の相関,または片方増えれば片方減る(逆に片方減れば片方増える)=負の相関なんて状況は,どっちかが原因で,どっちかが結果という因果関係がないと現れないはだから(細かい例外を除けば大概そうだと思う)。そうすると,「相関あり=(どっちが原因でどっちが結果かは不明だけども)因果あり」と言えると思います。すると,前者も後者もどっちも同じことを表してるから,どっちでもいいと言えるから。④前者の「因果があるように見えるけれど,(第…………」のところで,因果があるように見えると言ってるけど,それはつまり相関があるからで,これを踏まえると,前者は「相関があるけれど,因果はない」と言い換えられる。これを擬相関と呼ぶなら,「相関はあるけれど,因果はない」の例である,アイスが売れる→気温が上がるという,現象も擬相関と呼ぶことになってしまって,なんかおかしなことになると思うから。⑤「第3の変数の影響で,因果があるように見えるけれど,本当はは因果はない」という前者の意味を持ちだすときには,因果の有無云々のことを考えている時点で相関を暗に考慮している(因果を考えるには相関があることが前提だから)。つまり,前者の意味は因果の有無を考えると同時に相関のことも考えているも考えているので,前者も後者も実質同義。
以上のような理由で,後者の定義が好きなので,この記事でもこの意味で使い,そして話を2つに分けました。日本統計学会が後者の意味で使っているところを見ると,後者の意味が"間違い"とまではいかないはずので,本来の意味は前者かもしれないけどまあいいかなと思います(誤用が増えたことや,年月の経過によって別の意味でも使われるようになった日本語的な感じ)。
まとめ
それは擬相関かもしれない,背後に別の要因が存在していないか,よく考えよう!!
相関があったとしても因果もあるとは限らない!!
第3章 全体と部分で結果が違う
シンプソンのパラドックス(テストの平均点)
A高校の生徒とB高校の生徒に同一のテストを実施しました。その結果を,各高校ともに,男女別に集計,平均点を計算しました。その結果をまとめたのが以下の表です。
| 平均点 | A高校 | B高校 | 比較すると | |
|---|---|---|---|---|
| 男 | 80点 | 75点 | A > B | |
| 女 | 60点 | 55点 | A > B | |
| 全体 | ??? |
男女別にみると,男子の平均も女子の平均もどちらもA高校の生徒の方が優れています。
ここで問題です。
Q:男女合わせた全体の平均点が高いのはA高校?B高校?
.
.
.
.
.
.
.
.
.
.
正解は**「どちらともいえない」**です。
A高校の方が平均点が高いと思った人,はずれです。
実は,上の表だけではAが優れているとは必ずしも言えません。
つまり,B高校の方が平均点が高い可能性もあるのです。
B高校の方が平均が高いかもしれないという答えは直感ではなかなか受け入れがたいのではないでしょうか。そういう人のために具体例を見ていきましょう。この場合のポイントは生徒数です。
| 生徒数 | A高校 | B高校 |
|---|---|---|
| 男 | 30人 | 80人 |
| 女 | 70人 | 20人 |
| 全体 | 100人 | 100人 |
生徒数が上の表のようになっている場合,A高校とB高校の平均点$\bar{x_A}, \bar{x_B}$は以下のような式で計算されます。
\begin{eqnarray}
\bar{x_A} &=& \frac{80点 \times 30人 + 60点 \times 70人}{100} \\
&=& 66点 \\
\bar{x_B} &=& \frac{75点 \times 80人 + 55点 \times 20人}{100} \\
&=& 71点
\end{eqnarray}
**A高校の平均点$=66点$,B高校の平均点$=71点$**と言うわけで,A < Bとなりました!この例のように,生徒数によっては,B高校が勝つということもあり得るのです。もちろん,A高校が勝つこともあります。男女別でみるとA高校が勝ってるのに,全体で見るとB高校が勝っている,なんとも不思議な結果ですね~。
このように,部分で見るか,全体で見るかによって異なる結果が導かれる現象をシンプソンのパラドックスといいます。このパラドックスは知っていないと初見では必ず騙されます。
シンプソンのパラドックス(仕事の現場では)
さきほどは,問題としてあなたに問うたので何か裏があるのではと注意深くなり,騙されなかったかもしれません。タイトルにもパラドックスと書いてありますしね。これが,仕事の現場だったらどうでしょうか。
あなたは製薬会社で働いていて,血圧を下げる新薬の開発計画を任されました。あなたは,まず薬を作りその有効性を検証すべく,治験を行い100のデータを集めてみました。すると以下の散布図のような結果が得られました。
この散布図を見ると,データは全体にまんべんなく散らばっていて,前節で説明した相関は存在しません。本当は投与後の方が血圧が下がっていてほしいので,**右下がりになっていてほしかったわけです。**でも,実際は横一直線と言う感じでした。新薬開発失敗!!やり直し!!
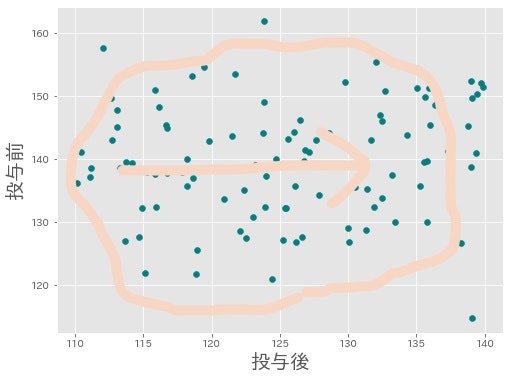
ですが,この図に情報を一つ加えると先ほどとは異なる結果が見えてきます。
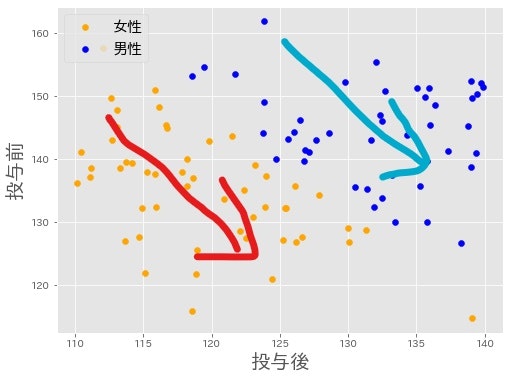
男女別に色分けしてみました。するとどうでしょう,どちらの性別も右下がりの傾向がある,つまり,投与後の方が血圧が改善されているという傾向があるではないですか!!
性別と言う情報を見逃していたら,あなたはせっかく作った新薬をスルーしていたことになります。危うく,人件費,研究費,製造費が無駄になって,上司に怒られていたところですね。
この例でもシンプソンのパラドックスが発生していました。つまり,全体で見ると薬の効果は無いように見えるが,性別ごとに見るときちんと効果があったということです。
まとめ
平均点の例,薬の効果の例の2つを見てみました。今回はシンプソンのパラドックスと言うタイトルをつけていたので,罠を見抜けたかもしれませんが,実際の仕事の現場ではどうでしょうか,セールスに遭った場合はどうでしょうか。パラドックスをきちんと見抜けますか?
パラドックスが存在しているかどうかを見抜くのは正直,簡単ではありません。ですが,このようなパラドックスが存在していることを知っておくだけでも,すこしは対策になります。よかったらぜひ覚えておいてください。
部分を見るか全体をみるかで結果が異なることがある!!
全体で見たり,部分に分けたり,いろいろな視点からデータを眺めよう!!
補足章 参考文献等
第4章
日本統計学会編 (2013). 日本統計学会公式認定 統計検定1級対応 統計学, pp132-133.
日本統計学会編 (2019). 統計検定1級 公式問題集 2014~2015年, pp126-127. {2014年 統計応用(医薬生物学)問2}