StanでCox回帰を実装する: 生存時間のベイズモデリング

慶應義塾大学・株式会社Nospareの菅澤です．
今回は生存時間分析で標準的な方法であるCox回帰をStanで実装してみます．

Cox回帰は頻度論的な推定手法としてパッケージ等で実装されていますが，近年では一般化ベイズと呼ばれる枠組みの中で利用することも可能になっています．Cox回帰をベイズ的に扱うことで，階層化などのモデルの拡張や，縮小事前分布などを使った変数選択とその不確実性評価，欠測データの扱いなどが比較的容易に行えます．

今回は，ベイズ的なCox回帰のStan実装と，欠測データを含んだケースでのベイズ的Cox回帰の利用について考えていきます．

Cox回帰の部分尤度

$i=1,...,n$に対して以下のデータが観測されていることを想定します．

• $y_i$: アウトカム (生存時間)

• $\delta_i$: センサリング変数 (1=イベント発生，0=センサリング)

• $x_i$: 説明変数ベクトル

Cox回帰 (Cox比例ハザードモデル) は$y_i$の条件付きハザード関数$h(t | x_i)$を

h(t | x_i)=h_0(t)\exp(x_i^\top \beta), \ \ \ \ i=1,\ldots,n.

のようにモデル化します．ここで，$h_0(t)$はベースラインハザードと呼ばれる関数です．

応用上，回帰係数$\beta$が興味の対象になることが多く，その場合$h_0(t)$は局外パラメータとして扱われます．$\beta$だけの尤度関数はCoxの部分尤度と呼ばれ，以下のような形で与えられます．

L(y;\beta,\delta, X)=\sum_{i=1}^n \delta_i\ell_i(y; \beta, X), \ \ \ \ \ 
\ell_i(y; \beta, X)=x_i^\top\beta - \log \left\{\sum_{j;\ Y_j\geq Y_i} \exp (x_j^\top \beta)\right\}.

ここで，$y=(y_1,\ldots,y_n)$および$\delta=(\delta_1,\ldots,\delta_n)$，$X=(x_1,\ldots,x_n)$です．

関数$L(y;\beta,\delta, X)$を$\beta$について最大化することで$\beta$の点推定値を得ることができます．

一般化ベイズ法

部分尤度をベイズ統計学の枠組みで扱うことで，モデルの拡張が比較的容易になったり，推定結果の不確実性評価を容易に行うことができます．部分尤度は通常の尤度関数とは異なるものですが，一般化ベイズと呼ばれる枠組みで扱うことが可能です．一般化ベイズ法のより詳しい解説についてはこちらの記事をご覧ください．

一般化ベイズの枠組みでは，$\beta$の一般化事後分布を

\pi(\beta|y,\delta,X)\propto \pi(\beta)\exp\left\{-\omega L(y;\beta,\delta, X)\right\}

のように定義します．ここで，$\pi(\beta)$は事前分布です．$\omega$はlearning rateと呼ばれるチューニングパラメータですが，今回は簡単のために$\omega=1$として考えます．

この事後分布は，$\beta$についての複雑な関数形になっていますが，Stanを使うことで簡単に事後サンプルを生成することができます．

モデルの拡張

ベイズの枠組みで扱うことで，（Stanで実装する場合は特に）比較的容易に追加的な構造を導入することができます． 今回は$x_i$の一部に欠測データが含まれている状況を想定して，従来のCox回帰の拡張を考えてみます．

まず，欠測構造として「無視可能な欠測 (ignorableまたはmissing at random)」を仮定します．このとき，ベイズの枠組みでは欠測値を潜在変数として扱うことができます．例えば，$x_i=(x_{i1},\ldots,x_{ip})$のうち$x_{i1}$が欠測している場合，$x_{i1}$に対して事前分布を与えて，MCMCの過程で$x_{i1}$もサンプリングすることで欠測部分を補完しながらパラメータ推定を行うことができます．

$X$を欠測部分$X_{\rm mis}$と観測部分$X_{\rm obs}$に分けると，以下の事後分布を考えることに相当します．

\pi(\beta, X_{\rm mis} \mid y, \delta, X_{\rm obs})\propto \pi(\beta)\pi(X_{\rm mis})\exp\left\{-\omega L(y; \beta, X)\right\}

Stanを用いる場合，欠測値がカテゴリカル変数などの離散変数の場合は実装することが困難になります．そのため，以下では欠測値は全て連続変数であることを想定します．

離散変数の欠測割合がそこまで大きくない場合など，無理やり連続変数だとみなしても実用上の大きな問題が生じないケースはありますが，離散の欠測変数を正しく扱いたい場合は自前でサンプリングのアルゴリズムを実装する必要があります．

Stanによる実装

欠測データの補完を組み込んだバージョンは以下のようにStanで実装できます．(Cox-missing.stanとして保存しておきます．)

data {
  int<lower=1> n;               // Number of observations
  int<lower=0> p;               // Number of covariates
  matrix[n, p] X;               // Covariate matrix
  real<lower=0> Y[n];           // Survival times
  int<lower=1, upper=n> R[n];   // Ranks for the risk set (1 = earliest event)
  int<lower=0, upper=1> C[n];   // Censoring indicator (1 = event, 0 = censored)
  int<lower=0> n_mis;                    // number of missing data points
  int<lower=1, upper=n> mis_row[n_mis];  // row indices of missing data
  int<lower=1, upper=p> mis_col[n_mis];  // column indices of missing data
}

parameters {
  vector[p] beta;               // Regression coefficients
  vector[n_mis] X_mis;  // missing data points as parameters
}

transformed parameters {
    matrix[n,p] XX = X;  
    for (i in 1:n_mis) {
        XX[mis_row[i], mis_col[i]] = X_mis[i];  // replace missing data with X_mis
    }
}

model {
  // Prior for missing data 
  X_mis ~ normal(0, 1); 
  
  // Normal prior for regression coefficients 
  beta ~ normal(0, 5);
  
  // Partial likelihood
  for (i in 1:n) {
    if (C[i] == 1) {            
      real eta = dot_product(XX[i], beta);         // Linear predictor
      real risk_sum = 0;

      // Calculate the sum of risk scores in the risk set
      for (j in i:n) {
        risk_sum += exp(dot_product(XX[R[j]], beta));
      }

      // Add contribution to partial likelihood
      target += eta - log(risk_sum);
    }
  }
}

上記のコードに関する補足

• 部分尤度を対数尤度として用いるため，target +=を使って直接対数尤度を定義しています．
• 欠測データの位置 (行番号と列番号の情報) をデータとして入力して，該当部分をパラメータとして定義しています．
• 説明変数が基準化されていることを想定して，欠測データに対する事前分布を標準正規分布にしています．(Stanでは連続変数しか扱えないため，欠測している変数は連続変数であるという暗黙の仮定を課しています．)
• 部分尤度を定義するために必要なリスク集合を与えるために，生存時間の順位の情報をデータRとして与える形にしています．

比較のため，完全データ (欠測がないデータ) に対するstanコード (Cox.stanとして保存) も以下に示しておきます．基本的に，上で示したコードから欠測変数を代入するパートを削除したものです．

data {
  int<lower=1> n;               // Number of observations
  int<lower=0> p;               // Number of covariates
  matrix[n, p] X;               // Covariate matrix
  real<lower=0> Y[n];           // Survival times
  int<lower=1, upper=n> R[n];   // Ranks for the risk set (1 = earliest event)
  int<lower=0, upper=1> C[n];   // Censoring indicator (1 = event, 0 = censored)
}

parameters {
  vector[p] beta;               // Regression coefficients
}

model {
  // Normal prior for regression coefficients 
  beta ~ normal(0, 5);
  
  // Partial likelihood
  for (i in 1:n) {
    if (C[i] == 1) {            
      real eta = dot_product(X[i], beta);         // Linear predictor
      real risk_sum = 0;

      // Calculate the sum of risk scores in the risk set
      for (j in i:n) {
        risk_sum += exp(dot_product(X[R[j]], beta));
      }

      // Add contribution to partial likelihood
      target += eta - log(risk_sum);
    }
  }
}

分析例

例として，今回はRのSurvivalパッケージに入っているlungデータ (肺がん患者の臨床試験データ) を解析していきます．基本的なデータの性質は以下の通りです．

• アウトカム: 診断後の生存日数 (イベント=死亡)
• 説明変数: 年齢，性別，体調に関するスコアなど7つの説明変数
• 約30%がセンサリングされている
• サンプルサイズは$228$だが，欠測データを含むサンプルを全て削除するとサンプルサイズが$168$まで減ってしまう

lungデータを二通りの方法（欠測値補完しながら解析する方法と完全データのみで解析する方法）で解析し，7つの説明変数に対する回帰係数の事後推測を行います．

library(rstan)
library(survival)

set.seed(1)

# Data
data(cancer)
Y <- lung$time
C <- lung$status - 1
X <- lung[,-(1:3)]
X$sex <- X$sex - 1
X <- apply(X, 2, scale)

# MCMC (with imputation) 
model1 <- stan_model("Cox-missing.stan")

n_mis <- sum(is.na(X))
Ind <- which(is.na(X), arr.ind=T)
X_stan <- X
for(i in 1:n_mis){
  X_stan[Ind[i,1], Ind[i,2]] <- (-100)
}

data1 <- list()
data1$n <- length(Y)
data1$p <- ncol(X)
data1$X <- X_stan
data1$Y <- Y
data1$C <- C
data1$R <- as.integer(rank(Y))
data1$n_mis <- n_mis
data1$mis_row <- Ind[,1]
data1$mis_col <- Ind[,2]

fit1 <- sampling(model1, data=data1, chain=1)
pos1 <- extract(fit1)

Beta1 <- apply(pos1$beta, 2, mean)
CI1 <- apply(pos1$beta, 2, quantile, prob=c(0.025, 0.975))

# MCMC (without missing)
model2 <- stan_model("Cox.stan")

om <- which(is.na(apply(X, 1, sum)))
data2 <- list()
data2$n <- length(Y[-om])
data2$p <- ncol(X[-om,])
data2$X <- X[-om,]
data2$Y <- Y[-om]
data2$C <- C[-om]
data2$R <- as.integer(rank(Y[-om]))

fit2 <- sampling(model2, data=data2, chain=1)
pos2 <- extract(fit2)

Beta2 <- apply(pos2$beta, 2, mean)
CI2 <- apply(pos2$beta, 2, quantile, prob=c(0.025, 0.975))

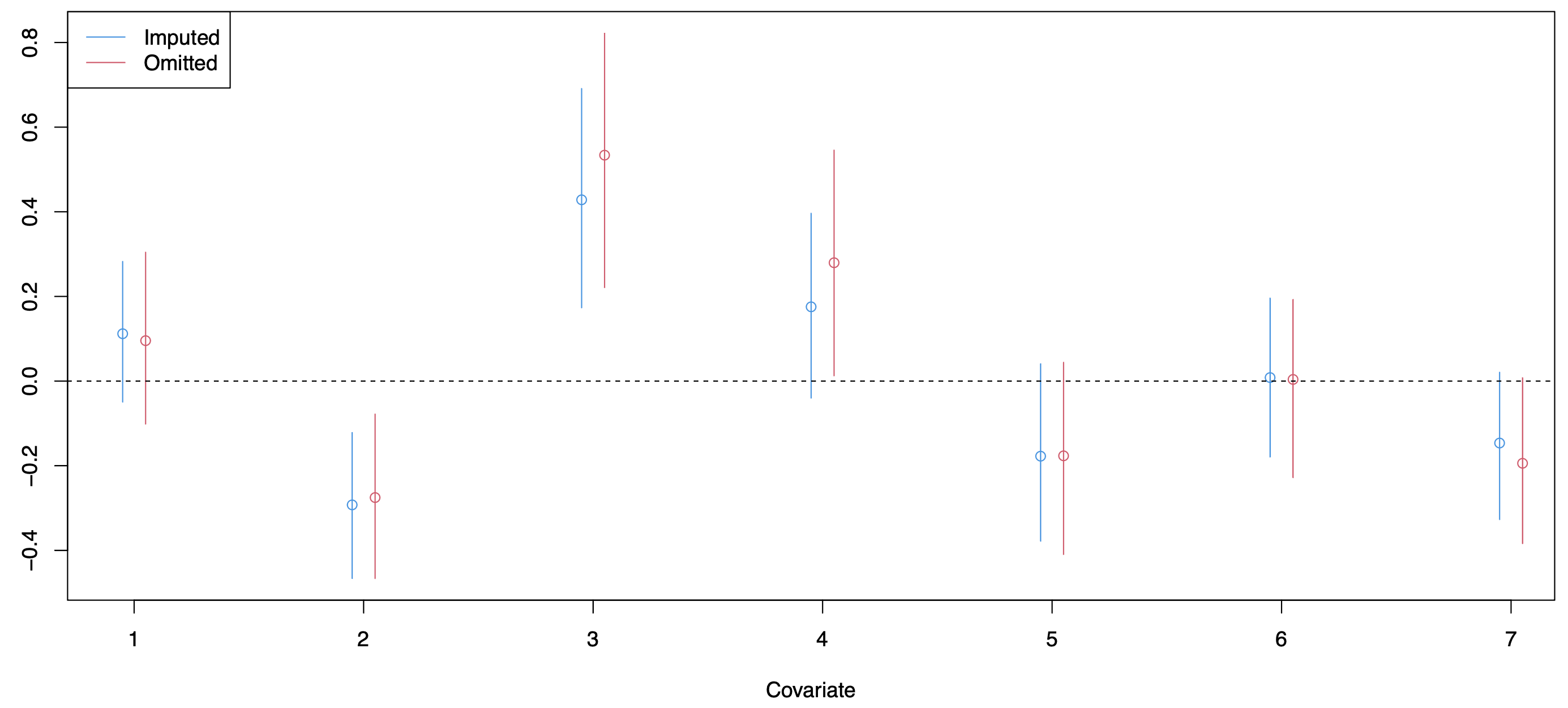
# Figure (posterior summary of coefficients) 
(p <- ncol(X))
plot((1:p)-0.05, Beta1, ylim=range(CI1, CI2), xlab="Covariate", ylab="", col=4)
points((1:p)+0.05, Beta2, col=2)
for(j in 1:p){
  lines(c(j,j)-0.05, CI1[,j], col=4)
  lines(c(j,j)+0.05, CI2[,j], col=2)
}
abline(h=0, lty=2)
legend("topleft", legend=c("Imputed", "Omitted"), col=c(4,2), lty=1)

上記のコードに関する補足

• Stanへ渡すデータにNAを含めることができないので，NA部分は-100という適当な数字に置き換えています．
• Stanによって生成される事後サンプルのサイズはデフォルトの数字 (2000回の繰り返しから半分をburn-inとして捨てた1000個の事後サンプル) にしています．

結果として，以下のような図が得られます．これは7つの回帰係数の事後平均と95%信用区間を図示したものです．

Imputedが欠測データ補完をした分析 (Cox-missing.stan)，Omittedが欠測を含むデータを全て削除した完全データでの分析 (Cox.stan) を表します．全体的に，Imputedの方が信用区間の幅がOmittedと比べて短くなっていることがわかります．これは，Imputedでは欠測値補完によって$228$個全てのデータを使えているのに対し，Omittedでは欠測値を含まない$168$個のデータだけを使っているため情報量が少なくなっていることが原因であると考えられます．

ちなみに，詳細は割愛しますが，生成された事後サンプルのトレースプロット等を確認すると相関の低いサンプルパスがStanによって生成できていることも確認できました．一方で，計算時間がそれなりに（自分のノートPCで10分くらい）かかりました．

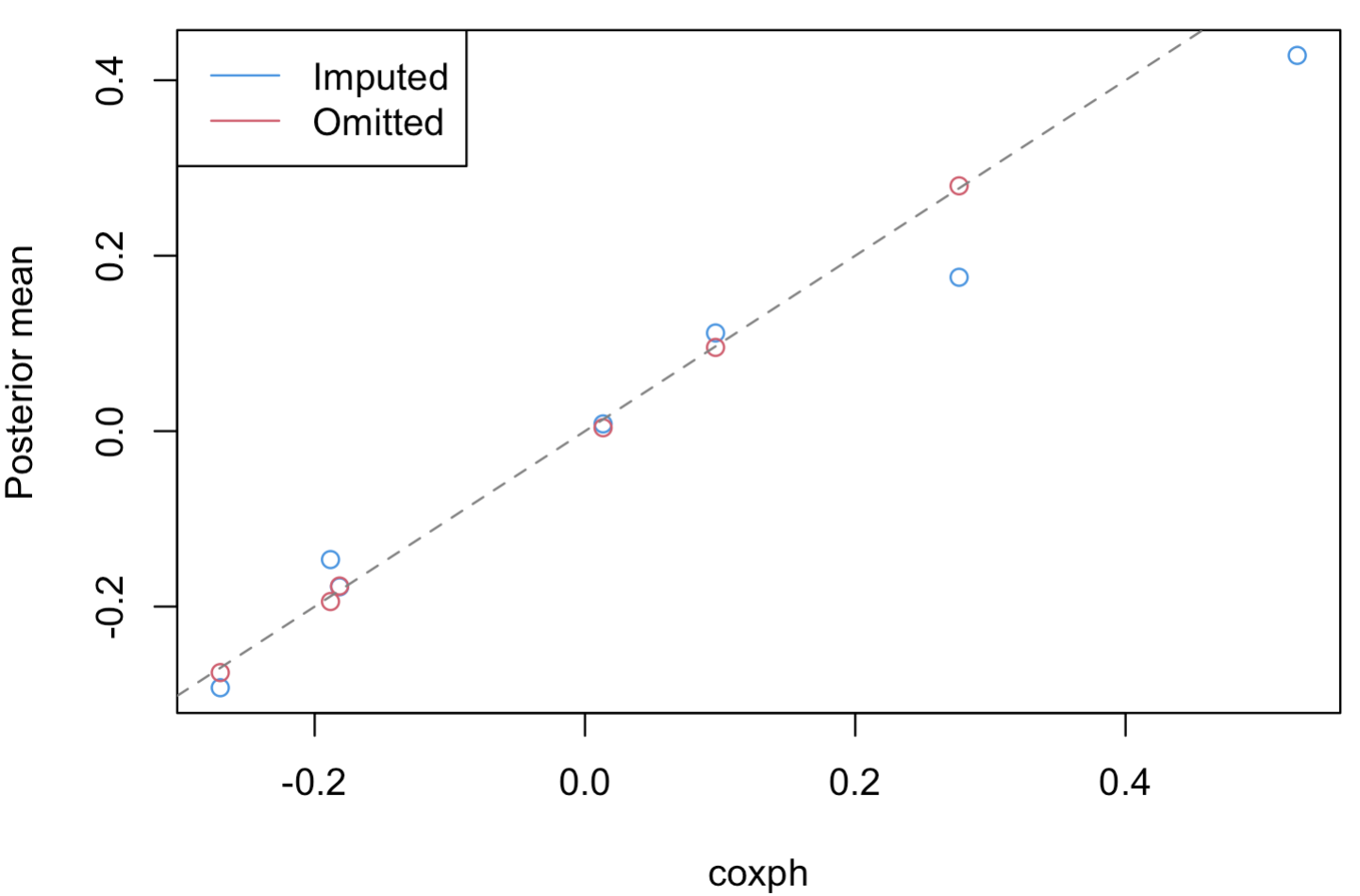
また，頻度論的にCox回帰を推定するツールとしてはsurvivalパッケージのcoxphという関数があります．この方法はOmittedのように欠損値を含まないデータのみで推定するものでして，Omittedと似たような結果になります．

おわりに

今回は説明変数の数が少なかったため回帰係数に対して単に情報の少ない事前分布を与えましたが，説明変数の数が多い状況では何らかの形で変数選択を実施することが望ましいです．ベイズモデリングの枠組みでは，回帰係数に対してラプラス事前分布や馬蹄事前分布などを与えることで回帰係数に対して柔軟な推定が可能となります．具体的にはStanコードでbetaに対する事前分布を変更することで容易に実装することができます．

今回はStanを使ってCox回帰を実装する方法を紹介しました．Stanを使ったモデリングの実装例については今後もいろいろと紹介していこうと考えています．

株式会社Nospareでは統計学の様々な分野を専門とする研究者が所属しております．統計アドバイザリーやビジネスデータの分析につきましては株式会社Nospareまでお問い合わせください．