東京大学・株式会社Nospareの菅澤です.
今回は状態空間モデルによる時系列予測手法を用いた因果効果の推定手法であるCausalImpactについて紹介します.
CausalImpactとは
CausalImpactはGoogleによって開発された因果効果推定の方法です.手法の詳細はBrodersen et al. (2015, AoAS)に記載されており,手法を実装したRパッケージも公開されています.
CausalImpactは,ある介入が時間変化するアウトカムにどのような影響を与えるかを推定(推測)するための手法です.時間変化するアウトカム(時系列データ)に対して因果効果を推定する有名な方法としてDifference-in-Difference (DID)がありますが,DIDよりも緩い仮定のもとで時間変化する因果効果を推定できる方法として知られています.
CausalImpactのコアのアイデアは 「介入前のデータから反実仮想(介入が行われていない仮想世界)のデータを補完して,実際の観測データと比較する」 です.
その際に,反実仮想のデータを精度高く補完することが肝になりますが,論文のタイトルにも記載されているように,状態空間モデルの一種であるBayesian structural time-series modelsを用いて補完(予測)することを提案しています.(以下では,このモデルを単に状態空間モデルと呼ぶことにします.)
設定
$t=1,\ldots,T+m$に対して,アウトカムを$y_{t}$,説明変数を$x_t$とします.($x_t$の候補としては,介入の影響を受けないものが好ましいとされています.)
また,時刻$T$に介入が生じたとします.そのため,時刻$T$以降のアウトカム$y_{T+1},\ldots,y_{T+m}$は介入の影響を受けた系列になります.CausalImpactでは,介入を受けていない反実仮想の系列$y^c_{T+1},\ldots,y^c_{T+m}$を状態空間モデルによって作り出すことを考えます.
具体的には,介入前のデータ$(y_t, x_t) (t=1,\ldots,T)$ から状態空間モデルを推定し,$x_{T+1},...,x_{T+m}$を用いて$y^c_{T+1},\ldots,y^c_{T+m}$を求めていきます.
注意: 状態空間モデルを用いて時刻$T$までのデータから時刻$T+m$までの系列を「予測」しているのですが,その期間には実際の観測データが既に得られており,見えない反実仮想の系列の補完のために用いています.そのため,日本語としてイメージが湧きやすいように以下では「予測」ではなく「補完」という言葉を使います.
補完モデル
系列$y_t$に対して,以下のような状態空間モデルを考えます.
\begin{aligned}
y_t=&Z_t^\top\alpha_t + \varepsilon_t, \ \ \ \ \varepsilon_t\sim N(0, \sigma_t^2),\\
\alpha_{t+1}=& T_t\alpha_t + R_t\eta_t , \ \ \ \ \eta_t\sim N(0, Q_t).
\end{aligned}
ここで,$\varepsilon_t$および$\eta_t$ ($q$次元)は時間ごとに独立な誤差項です.$\alpha_t$は$d$次元の状態変数(時系列構造を決める重要な確率変数)であり,その線形結合$Z_t^\top\alpha_t$に誤差$\varepsilon_t$が乗って実際の観測$y_t$が得られる構造になっています.
このモデルは非常に一般的な形で表現されています.実際に使う場合は,捉えたい$y_t$の時系列構造に応じて,$Z_t$(ベクトル), $T_t$($d\times d$行列), $R_t$($d\times q$行列)および$Q_t$($q\times q$行列)の具体的な形を指定したり,推定する必要があります.また,説明変数$x_t$は多くの場合$Z_t$の一部としてモデルに組み込まれます.
具体的なイメージを持つために簡単なモデルを1つ考えてみます.説明変数$x_t$は1次元(スカラー)で,日次でデータが観測されているとします.このとき,以下の3つの要素に着目して$y_t$をモデル化することを考えてみます.
要素1. $y_t$の時間トレンド
要素2. $x_t$が$y_t$に与える影響
要素3. 祝日・休日が$y_t$に与える影響
上記の点を考慮したモデルの一例は以下の通りです.
\begin{align}
y_t&=\mu_{t}+\beta_{t}x_t+\gamma_{t}d_t+\varepsilon_t, \ \ \ \varepsilon_t\sim N(0, \sigma^2) \\
\mu_{t+1}&=\mu_t+\delta_t+\eta_{\mu, t}, \ \ \ \delta_{t+1}=\delta_t+\eta_{\delta,t}, \ \ \ \eta_{\mu,t}\sim N(0, \sigma_\mu^2), \ \ \eta_{\delta,t}\sim N(0, \sigma_\delta^2), \tag{1} \\
\beta_{t+1}&=\beta_t+\eta_{\beta,t}, \ \ \ \eta_{\beta,t}\sim N(0,\sigma_\beta^2), \\
\gamma_{t+1}&=\gamma_t+\eta_{\gamma,t}, \ \ \ \eta_{\gamma,t}\sim N(0,\sigma_\gamma^2). \\
\end{align}
ここで,$d_t$は祝日・休日のときに1になり,それ以外で0となるダミー変数です.
上記のモデルにおいて,$\mu_t, \beta_t$および$\gamma_t$が潜在変数になりますが,それらの役割は以下の通りです.
- $\mu_t$: $x_t$および$d_t$では捉えきれない時間トレンド (要素1に対応) ⇨ 局所線形トレンドでモデル化
- $\beta_t$: $x_t$が与える時変の影響 (要素2に対応) ⇨ ランダムウォークでモデル化
- $\gamma_t$: $d_t$が与える時変の影響 (要素3に対応) ⇨ ランダムウォークでモデル化
$\mu_t$に対するモデルは$\mu_{t+1}-\mu_t=\delta_t+\eta_{\mu,t}$と書くことができますので,$\mu_t$の一階差分にランダムウォークを入れたモデルと解釈することができます.このようにモデル化することで,局所的に$\mu_t$が線形関数になる (全体では非線形に動く) 柔軟なモデルができます.
また,$\beta_t$や$\gamma_t$は必ずしも時間変化させる必要はなく,$\beta_t=\beta$および$\gamma_t=\gamma$として定数のパラメータとしてモデル化することも可能です.その場合,上記のモデルでは$\sigma_\beta^2=0$および$\sigma_\gamma^2=0$とすることに相当します.
モデル(1)は冒頭で出した一般形で表現することができます.具体的には,$Z_t=(1, 0, x_t, d_t)$,$\alpha_t=(\mu_t, \delta_t, \beta_t, \gamma_t)$,$\sigma_t=\sigma^2$,$R_t=I_4$, $Q_t=diag(\sigma_\mu^2, \sigma_\delta^2, \sigma_\beta^2, \sigma_\gamma^2)$および
T_t=\left(\begin{array}{cccc}
1 & 1 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{array}\right)
と設定した状態空間モデルとみなすことができます.
状態空間モデルを推定する汎用的なパッケージを使う必要がある際には,おそらく一般形での特定化が必要になると思いますが,例えばstanによる実装を考える場合は具体的なモデルの形をそのまま記述するだけですので,一般形との関係性を考える必要はありません.
また,CausalImpactのパッケージ内ではデフォルトで用いる状態空間モデルが指定されている点にも注意が必要です. パッケージの説明文によると,モデル(1)よりも簡素なモデル ($\mu_t, \beta_t, \gamma_t$を全て時間変化しない定数パラメータと想定したモデル) がデフォルトのモデルとして指定されているようです.今回の説明であまり触れていませんが,周期性(1週間ごとの周期的なトレンドなど)もCausalImpactのパッケージでは指定できます.
説明文の中では,より柔軟な状態空間モデルを使いたい場合はbstsパッケージの利用が推奨されています.このパッケージはBayesian structured time-series modelsを当てはめるためのパッケージです.
推定と補完
$y_t$に対するモデルの形を決めたら,$T$期までのデータを使って状態空間モデルを推定します.例えばモデル(1)の場合,分散パラメータ$\sigma^2, \sigma_\mu^2, \sigma_\delta^2, \sigma_\beta^2, \sigma_\gamma^2$と潜在変数の初期値(パラメータ)$\mu_1, \delta_1, \beta_1, \gamma_1$に対する事前分布を設定し,マルコフ連鎖モンテカルロ法(MCMC)によってパラメータおよび潜在変数の事後分布を計算します.
考えているモデルが線形ガウスの状態空間モデルのため,ギブスサンプリングなどで簡単にMCMCを行うこともできますが,既存のパッケージやstanを用いても同じようにMCMCを実行することができます.
パラメータと潜在変数の事後サンプルを得ることができれば,あとはモデルの構造にしたがって$x_{T+1},\ldots,x_{T+m}$を用いて$y^c_{T+1},\ldots,y^c_{T+m}$の予測分布からサンプルを生成します.これにより,反実仮想のデータ$y^c_{T+1},\ldots,y^c_{T+m}$を補完することができるため,あとは単純に実際の観測データ$y_{T+1},\ldots,y_{T+m}$を比較をすることで介入の効果を推定することができます.
冒頭でも述べたように, CausalImpactの手法としての本質は「状態空間モデルによる反実仮想の補完」 ですので,補完ができた後は興味のある量について計算するだけでOKです.例えば,介入効果の時間変化を見たい場合は,$t=T+1,\ldots,T+m$に対して$y_t-y^c_t$について注目し,$y^c_t$の事後予測分布からのサンプルからこの量の事後サンプルを生成することができます.
注意点として,(冒頭でも述べましたが)補完に使う説明変数$x_t$は介入の影響を受けないものを選ぶのが望ましいです.もし$x_t$が介入による影響を受けてしまった場合,補完された$y_{T+1}^c,\ldots,y_{T+m}^c$も介入の影響を受けてしまう可能性があり,反実仮想の補完として妥当ではなくなってしまいます.
CausalImpactのイメージ
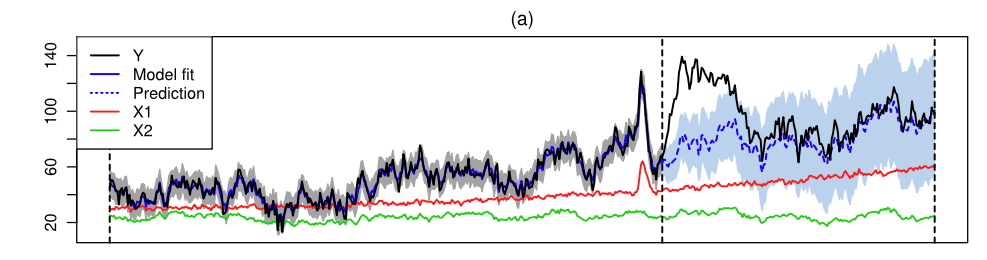
以下の2つの図はBrodersen et al. (2015, AoAS)のFigure 1を抜粋したものです.
図の中央部の点線が介入のタイミングを表しています. 実際の観測$Y$が実際の観測,$X1, X2$が説明変数です.介入前の青の実線が,状態空間モデルによって平滑化された観測値に対応しており,推定されたモデルによる予測(反実仮想の補完)が介入後の青の点線です.介入後に黒線と青点線に乖離がありますが,これが介入の効果として解釈できます.
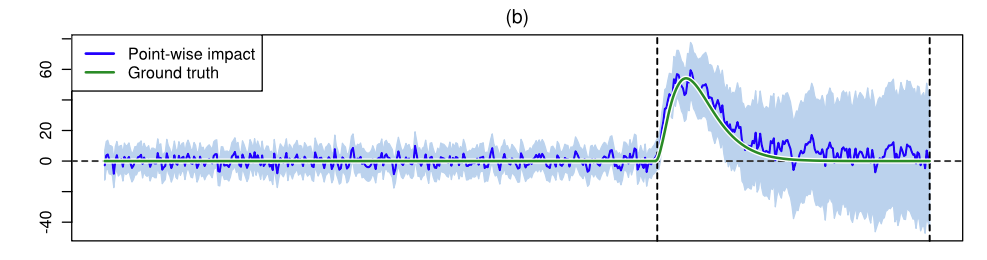
図の青線は介入の効果(実際の観測と補完した観測の差分)を表しています.この例はシミュレーションデータに基づいておりますので,真の効果が緑線として表示されています.介入の効果の時間変化をCausalImpactが適切に捉えていることがわかります.
また,図中の薄い青色の領域は各時刻における介入効果の95%区間を示しています.このように,状態空間モデルをMCMCで推定した手法を用いることで,興味のある量の事後サンプルに基づく直感的な推測も行えます.
CausalImpactの利点と限界
最後にCausalImpactの利点と限界についてまとめておきます.
CausalImpactの利点
- 介入効果の時間変化を捉えることができる
- 複数の説明変数の影響や時間トレンド,自己相関を柔軟に扱うことができる (状態空間モデルを使っている利点)
- パラメータに対する事前情報を導入することができる (ベイズ的なアプローチでは共通の利点)
最初の2つの利点はDIDに対する利点としても捉えることができます.
また,ある一定期間介入をした場合の効果もCausalImpactでは測ることができます.その場合も考え方は変わらず,介入前のデータを用いて介入後の反実仮想のデータを補完すればOKです.そのような具体例はBrodersen et al. (2015, AoAS)で扱われています.
CausalImpactの限界
-
「介入をした」ことに対する因果効果のみを推定している
例えば,広告効果測定などでは,異なった量の広告を複数回実施する可能性が考えられますが,広告量(介入の度合い)による因果効果の違いまで考えたい場面に対してCausalImpacatは直接的に対応することはできません. -
補完する期間が長いと精度が不安定になる可能性がある
時系列予測を考えているため,介入までの期間$T$に対して補完する期間$m$が大きい場合,補完の精度は高くないことが想定されます.また,補完の精度は$y_t$をうまく説明する$x_t$の存在の有無にも大きく左右される可能性があります.
おわりに
今回は時間変化するアウトカムに対して因果効果を推定するCausalImpactについて紹介しました.途中でも述べているように,この方法は「反実仮想のデータをモデルによって補完する」が本質的なアイデアです.そのため,CausalImpact自体は時系列データに対する方法ですが,アイデア自体は時系列に限らない文脈でも有効である可能性があります.
また,時系列データを用いて広告効果を推定する関連手法として,マーケティングの文脈ではMedia Mix Modeling (MMM) という方法もよく知られています. 今後機会があればこちらも紹介していこうと思います.
株式会社Nospareでは統計学の様々な分野を専門とする研究者が所属しております.統計アドバイザリーやビジネスデータの分析につきましては株式会社Nospareまでお問い合わせください.