慶應義塾大学・株式会社Nospareの菅澤です.
今回はガウス過程を用いた空間データの(階層)ベイズモデリングに関して,MCMCを用いた具体的なアルゴリズムの詳細について解説します.
空間データの階層モデリングに関する一般的な導入やモデルの説明については前の記事をご参照ください.
空間効果モデル
$y_i$を被説明変数,$x_i$を説明変数 (ベクトル) として,以下のようなモデルを考えます.
y_i=x_i^\top \beta + \omega_i + \varepsilon_i, \ \ \ \ \varepsilon_i\sim N(0, \sigma^2), \ \ \ i=1,\ldots,n.
ここで,$\omega_i$は各地点固有の切片項で,各地点における相場感を表現するパラメータです.$\omega_i=0$の場合 (空間効果がない場合),通常の線形回帰モデルになります.
以下の議論では,ベクトルによるモデルの表現を用意しておくと便利です.
y=X\beta + \omega +\varepsilon, \ \ \ \ \varepsilon\sim N(0, \sigma^2 I_n).
空間効果$\omega_i$に対しては,ガウス過程に基づく確率モデル
\omega\equiv (\omega_1,\ldots,\omega_n)\sim N(0, \tau^2 C(\phi))
を導入します.$C(\phi)$は$n\times n$の相関行列で各地点同士の距離によって決まる行列です.(ガウス過程と空間効果についての導入は前の記事を参照してください.)
今回は,上記のモデルのパラメータ$\beta, \sigma^2, \tau^2,\phi$および空間効果$\omega$の事後分布を計算するためのMCMCアルゴリズムを考えていきます.
事前分布として,$\beta\sim N(A_\beta, B_\beta), \sigma^2\sim {\rm IG}(a_{\sigma}, b_{\sigma}), \tau^2\sim {\rm IG}(a_\tau, b_\tau)$を与えると,これらは条件付き共役な事前分布となります.一方で,レンジパラメータ$\phi$に対して扱いやすい(条件付き)共役事前分布は存在しません.事前分布の設定としてはいくつか候補がありますが,今回は一様事前分布$U(0, \phi_{\rm max})$を用います.ここで,$\phi_{\rm max}$は適当な上限の値で,観測地点間の距離の最大値などを用いて決めておきます.
MCMCアルゴリズム1: ギブスサンプラー
上記のような事前分布のもと,同時事後分布は以下のように表現できます.
\pi(\beta, \sigma^2, \tau^2,\phi, \omega \mid D)\propto (\sigma^2)^{-a_\sigma-n/2-1}(\tau^2)^{-a_\tau-n/2-1}|C(\phi)|^{-1/2}
\exp\left\{-\frac{1}{2\sigma^2}(y-X\beta-\omega)^\top (y-X\beta-\omega)-\frac1{2\tau^2}\omega^\top C(\phi)^{-1}\omega-\frac12(\beta-A_{\beta})^{\top}B_{\beta}^{-1}(\beta-A_{\beta})-\frac{b_{\sigma}}{\sigma^2}-\frac{b_{\tau}}{\tau^2}\right\}
ここで,$D$は観測データの集合です.以上の分布でそれぞれのパラメータの比例部分のみを抽出することで,完全条件付き分布を以下のように求めることができます.
- $\beta\mid{\rm others}\sim N(A_{\beta,\ pos}, B_{\beta,\ pos})$, $A_{\beta, \ pos}=(X^\top X/\sigma^2+B_{\beta}^{-1})^{-1} (X^\top (y-\omega)/\sigma^2+B_{\beta}^{-1}A_{\beta} )$, $B_{\beta,\ pos}=(X^\top X/\sigma^2+B_{\beta}^{-1})^{-1}$
- $\omega\mid{\rm others}\sim N(A_{\omega,\ pos}, B_{\omega,\ pos})$, $A_{\omega,\ pos}=(I_n/\sigma^2 + C(\phi)^{-1}/\tau^2)^{-1}(y-X\beta)/\sigma^2$, $B_{\omega,\ pos}=(I_n/\sigma^2 + C(\phi)^{-1}/\tau^2)^{-1}$
- $\sigma^2\mid{\rm others}\sim {\rm IG}\left(a_{\sigma}+\frac{n}{2}, b_{\sigma}+\frac12(y-X\beta-\omega)^\top (y-X\beta-\omega)\right)$
- $\tau^2\mid{\rm others}\sim {\rm IG}\left(a_{\tau}+\frac{n}{2}, b_{\tau}+\frac12\omega^{\top}C(\phi)^{-1}\omega\right)$
- $\pi(\phi\mid{\rm others})\propto |C(\phi)|^{-1/2}\exp (-\frac1{2\tau^2}\omega^\top C(\phi)^{-1}\omega)I(\phi\in(0, \phi_{\rm max}))$
$\phi$の完全条件付き分布からのサンプリングとして,例えばrandom-walk MHアルゴリズムを使うことができます.
導出した完全条件付き分布からの乱数生成を繰り返すこと (ギブスサンプラー) で,同時事後分布からのサンプルを生成することができます.このような事後サンプルを用いることで,パラメータの点推定値や信用区間が導出できます.
MCMCアルゴリズム2: MHアルゴリズム
上記のギブスサンプラーでは,未知パラメータと空間効果の事後サンプルを同時に生成するアルゴリズムでしたが,2段階で事後サンプルを生成する方法も用いられることがあります.具体的には,はじめに未知パラメータの周辺事後分布$\pi(\beta, \sigma^2, \tau^2,\phi \mid D)$から事後サンプルを生成し,次に空間効果の条件付き事後分布$\pi(\omega \mid \beta, \sigma^2, \tau^2,\phi, D)$から事後サンプルを生成する方法です.
空間効果の条件付き事後分布はギブスサンプラーで用いた分布と同様ですので,未知パラメータの周辺事後分布を考えていきます.前の記事で与えたように,$y$の周辺分布は$y\sim N(X\beta, \Sigma(\sigma, \tau, \phi)), \Sigma(\sigma, \tau, \phi)=\tau^2 C(\phi)+\sigma^2I_n$となります.したがって,未知パラメータの周辺事後分布は
\pi(\beta, \sigma^2, \tau^2,\phi|D)\propto (\sigma^2)^{-a_{\sigma}-1}(\tau^2)^{-a_{\tau}-1}|\Sigma(\sigma, \tau, \phi)|^{-1/2}\exp\left\{-\frac12(y-X\beta)^\top \Sigma(\sigma, \tau, \phi)^{-1}(y-X\beta)-\frac12(\beta-A_{\beta})^{\top}B_{\beta}^{-1}(\beta-A_{\beta})-\frac{b_{\sigma}}{\sigma^2}-\frac{b_{\tau}}{\tau^2}\right\}
となります.この場合,$\beta$の完全条件付き分布は$N(A_{\beta,\ pos}, B_{\beta,\ pos})$
A_{\beta, \ pos}=(X^\top\Sigma^{-1} X+B_{\beta}^{-1})^{-1} (X^\top\Sigma^{-1}y+B_{\beta}^{-1}A_{\beta} ), \ \ \ \ \
B_{\beta,\ pos}=(X^\top \Sigma^{-1}X+B_{\beta}^{-1})^{-1}
となりますが,$(\sigma^2, \tau^2,\phi)$の完全条件付き分布は簡単な分布にはなりません.そのため,random-walk MHアルゴリズムなどを用いたサンプリングが必要です.
アルゴリズム1の利点として,ほぼ全てのパラメータを簡単な分布からサンプリングできるのに対し,欠点として,$\phi$の値が大きいときに$C(\phi)$の逆行列が数値的に不安定になる点が挙げられます.
一方で,アルゴリズム2では$C(\phi)$の代わりに$\Sigma(\sigma,\tau,\phi)$の逆行列を扱うことになりますが,こちらは$\sigma^2 I_n$が追加されている効果で安定的に逆行列を計算することが可能です.ただし,その代償として,$(\sigma^2, \tau^2,\phi)$の完全条件付き分布が良く知られた形にならず,MHアルゴリズムに頼らざるを得ないという欠点が出てきます.
予測分布の計算
パラメータと空間効果の事後サンプルが生成できた状況で,未観測地点の予測を考えます.設定として,$s_0$を新しい地点の位置情報,
$x_0$をその地点での説明変数とします.
まずは新しい地点における空間効果を求めます.背景にガウス過程を考えている利点として,予測地点と観測地点が何個あったとしても統一的に同時分布を与えることができます.(これはガウス過程の定義に由来するものです.)
$\omega_0$を地点$s_0$での空間効果とします.すると,$(\omega_0, \omega^\top)^\top$の同時分布は平均0,分散共分散行列が
\tau^2\left(
\begin{array}{cc}
1 & z(\phi)^\top \\
z(\phi) & C(\phi)
\end{array}
\right)
の多変量正規分布になります.ここで
ここで,$z(\phi)=(\rho(||s_0-s_1||;\phi),\ldots,\rho(||s_0-s_n||;\phi))^\top$ ($s_0$と観測地点$s_1,\ldots,s_n$の相関を並べたベクトル) です.すると,多変量正規分布の条件付き分布の公式から,$\omega$および未知パラメータを所与としたときの$\omega_0$の条件付き分布は
\omega_0|\omega,\phi,\tau^2\sim N\left(z(\phi)C(\phi)^{-1}\omega, \tau^2-\tau^2 z(\phi)^\top C(\phi)^{-1}z(\phi)\right)
となります.$\omega_0$が所与のもとで,未観測データ$y_0$の条件付き予測分布は
y_0|\omega_0, \beta,\sigma^2 \sim N(x_0^\top \beta+\omega_0, \sigma^2)
となります.このように,$\omega_0$と$y_0$を段階的に乱数生成することで,予測分布から乱数生成を行うことができます.
Rでやってみる
空間効果モデルはRパッケージspBayesによって簡単に使うことができます.(もちろん上記のMCMCアルゴリズムを自前で実装する形でも使えます.)
ここでは,Boston housing dataを用いた簡単な例を紹介します.
データをトレーニングデータとテストデータに分け,トレーニングデータから空間回帰モデルを推定し,テストデータをどの程度予測できるかを確認します.また,同様のことを通常の線形回帰モデルでも行い,空間効果を導入することによる予測精度の違いを検討してみます.
# パッケージ
library(spBayes)
library(mlbench)
# データのロード
data(BostonHousing2)
data <- BostonHousing2
Sp <- as.matrix(data[,c("lat", "lon")])
# トレーニング・テストデータの分割
set.seed(1)
n <- dim(data)[1]
m <- 100 # number of out-of-samples
om <- sort( sample(1:n, m) )
data_train <- data[-om,]
data_test <- data[om,]
Sp_test <- Sp[om,]
Sp_train <- Sp[-om,]
Y_test <- data$cmedv[om]
X <- data[,c(7,9, 11:19)]
X_test <- as.matrix(X[om,])
トレーニングデータに対して'spBayes'の'spLM'関数を用いて空間回帰モデルを適用します.さらに'spPredict'関数でテストデータの予測を行います.
# 空間回帰モデル
formula <- as.formula(cmedv~crim+indus+nox+rm+age+dis+rad+tax+ptratio+b+lstat)
starting <- list("phi"=0.02, "sigma.sq"=50, "tau.sq"=1)
tuning <- list("phi"=0.1, "sigma.sq"=0.1, "tau.sq"=0.1)
priors <- list("beta.Norm"=list(rep(0,12), diag(1000,12)),
"phi.Unif"=c(0.01, 0.5), "sigma.sq.IG"=c(1, 1),
"tau.sq.IG"=c(1, 1))
cov.model <- "exponential"
n.report <- 500
n.samples <- 2000
burn.in <- 0.5*n.samples
mcmc_train <- spLM(formula, data=data_train, coords=Sp_train, starting=starting, tuning=tuning, priors=priors,
cov.model=cov.model, n.samples=n.samples, verbose=T, n.report=n.report)
mcmc_train <- spRecover(mcmc_train, start=burn.in, verbose=FALSE)
# 予測分布
Pred.pos <- spPredict(mcmc_train, pred.coords=Sp_test, pred.covars=cbind(1, X_test), verbose=T, n.report=n.report)[[1]]
Pred.pos <- Pred.pos[,-(1:burn.in)]
Pred.SPR <- apply(Pred.pos, 1, mean) # 点予測
PI.SPR <- apply(Pred.pos, 1, quantile, prob=c(0.025, 0.975)) # 区間予測
トレーニングデータから推定された空間効果を可視化します.
# 空間効果の可視化
effect <- apply(mcmc_train$p.w.recover.samples, 1, mean)
xx <- (effect - min(effect)) / diff(range(effect)) # scaling
cs <- colorRamp( c("blue", "green", "yellow", "red"), space="rgb" )
cols <- rgb( cs(xx), maxColorValue=256 )
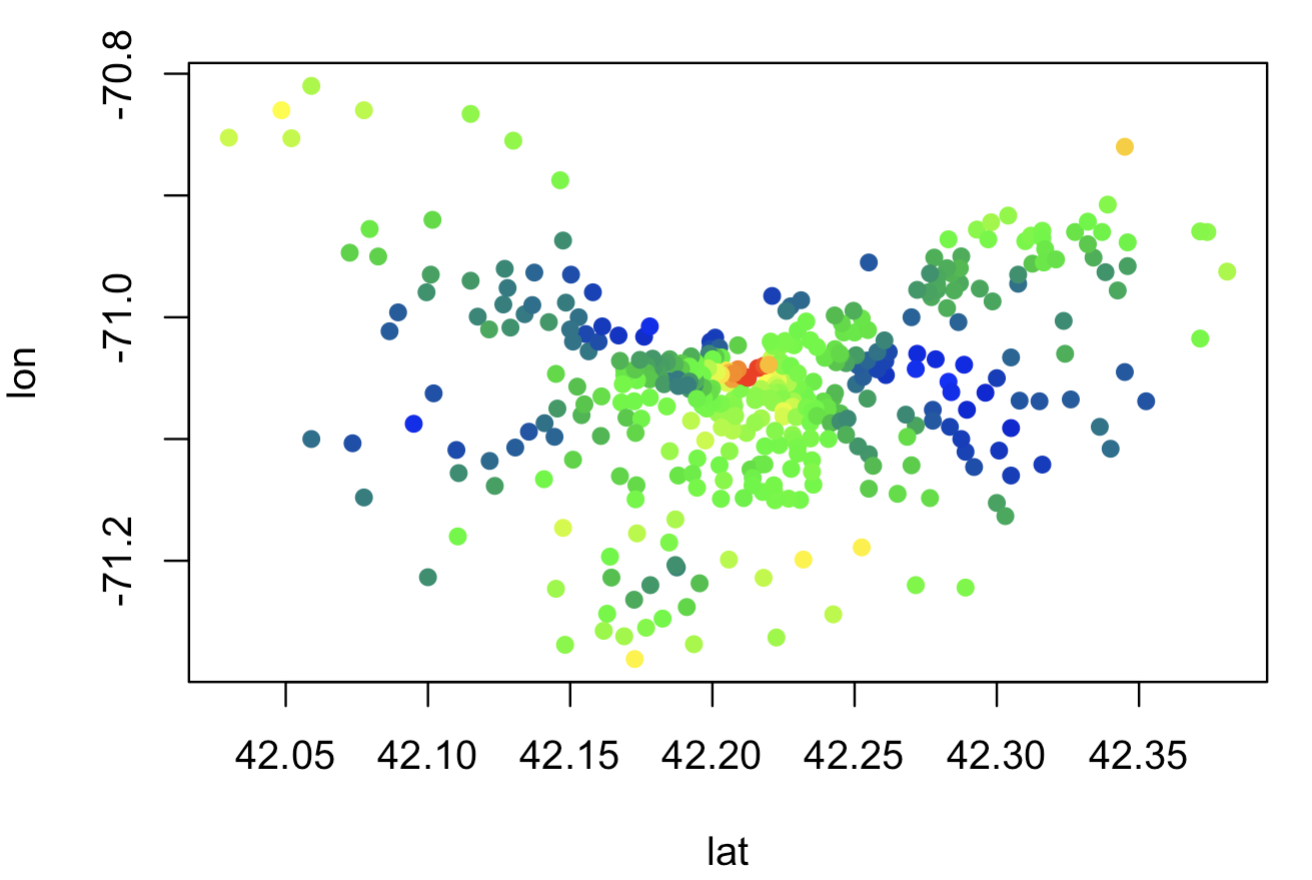
plot(Sp_train, col=cols, pch=16, cex=1)
こちらを実行すると以下のような結果が得られます.(赤い点ほど値が高く,青いほど値が低いことを表します.)
この結果から見えない空間的なトレンドがある程度うまく捉えられていることがわかります.次に,線形回帰モデルとの予測精度の比較を行います.
# 標準的な回帰モデル
lm_train <- lm(formula, data=data_train)
Pred.LM <- predict(lm_train, newdata=data_test)
# 平方根平均二乗誤差
sqrt( mean((Y_test - Pred.SPR)^2) )
sqrt( mean((Y_test - Pred.LM)^2) )
# 被覆確率
mean(PI.SPR[1,]<Y_test & PI.SPR[2,]>Y_test)
こちらを計算すると,空間回帰モデルと通常の回帰モデルのMSEがそれぞれ3.75および4.54でした.空間効果を考慮することで,より精度の高い予測が実現できることがわかりました.
おわりに
今回は空間回帰モデルにおけるMCMCアルゴリズムの詳細と,Rによる簡単なデモを紹介しました.
株式会社Nospareでは統計学の様々な分野を専門とする研究者が所属しております.統計アドバイザリーやビジネスデータの分析につきましては株式会社Nospareまでお問い合わせください.