はじめに
DeepLearningを学び出してから2週間ほど経ちました。そろそろ学んだことが頭から零れ落ちる音がしてきたので、整理がてらにアウトプットしたいと思います。今回から複数回に渡ってDNNを構築していきます。今回はフォワードプロパゲーション編です。
作成するDNNについて
画像が猫である(1)かそれ以外である(0)かを判定するネットワークを構築します。
使用するデータ
209枚の画像をトレーニングデータとし、50枚の画像をテストデータとして使用します。それぞれの画像のサイズは64 * 64です。
Number of training examples : 209
Number of testing examples : 50
Each image is of size : 64 * 64
また、正解データと不正解データの割合は以下のようになっています。
Number of cat-images of training data : 72 / 209
Number of cat-images of test data : 33 / 50
構築するDNN
レイヤ数
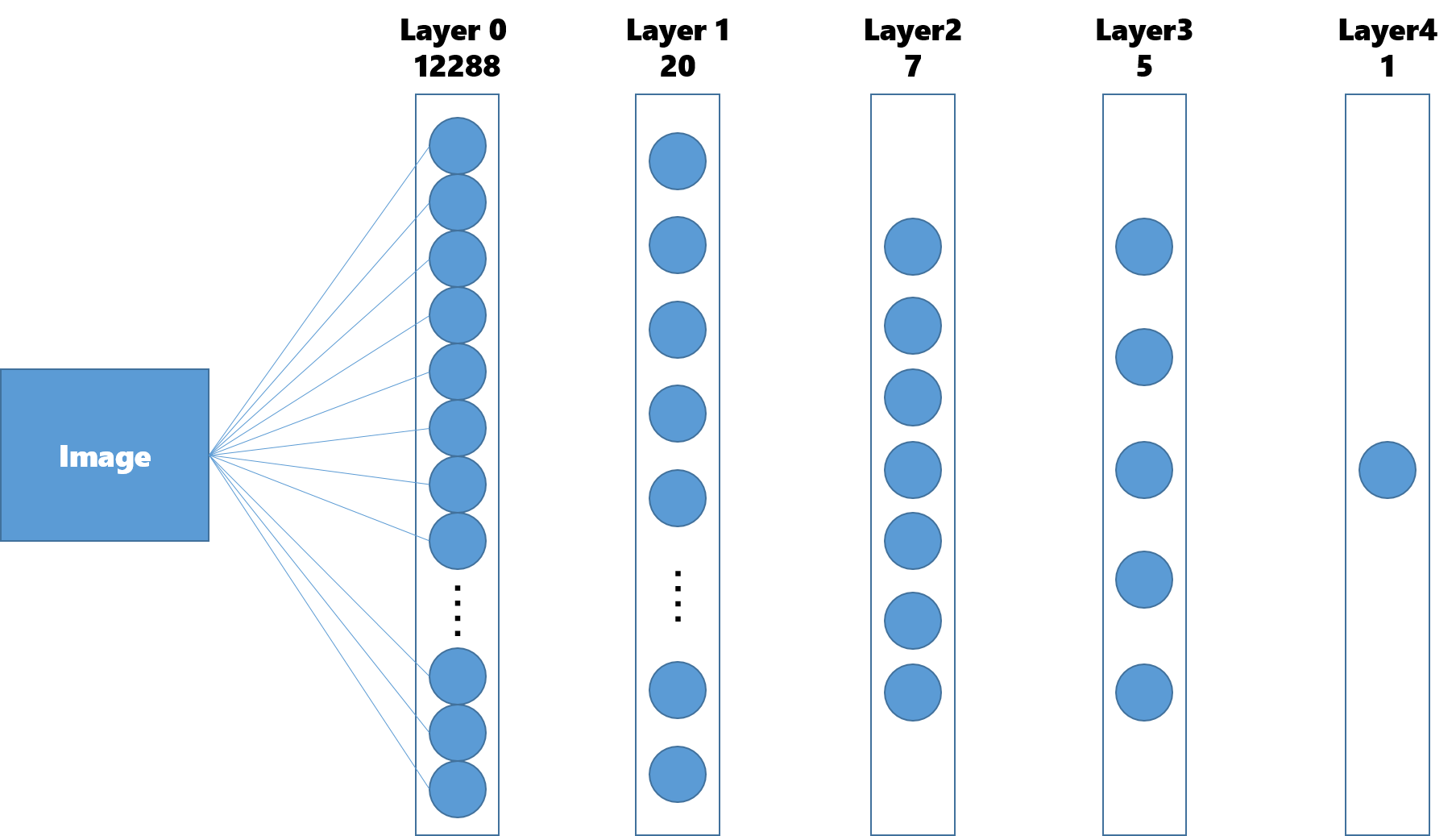
12288(64 * 64)の入力ノードと一つの出力ノードを持つ4層のネットワークを構築します。それぞれのノードを線で結ぶつもりだったのですがパワポで作るのは過酷だったのであきらめました。
Dimention of each layer : [12288, 20, 7, 5, 1]
活性化関数
今回は中間層にReLU関数を使い、出力層にsigmoid関数を使用します。
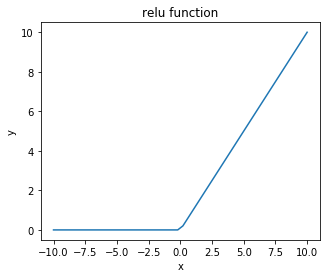
Relu関数
Relu関数は入力値が0以下であれば0を、それ以外であれば入力値をそのまま出力する関数です。以下のように書けます。
y = np.maximum(0, x)
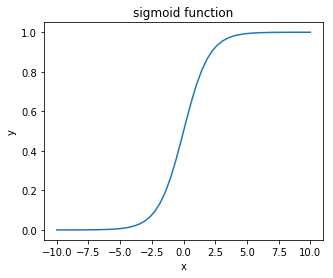
sigmoid関数
sigmoid関数は入力値を1から0の値に変換して出力する関数です。以下のように書けます。式で表すと次のようになります。
$$ y = \frac{1}{1+e^{-z}} $$
Pythonで書くと以下のようになります。
y = 1 / (1 + np.exp(-x))
学習の全体像
DNNの全体設計がわかったところで、DNNの学習について復習しておきます。
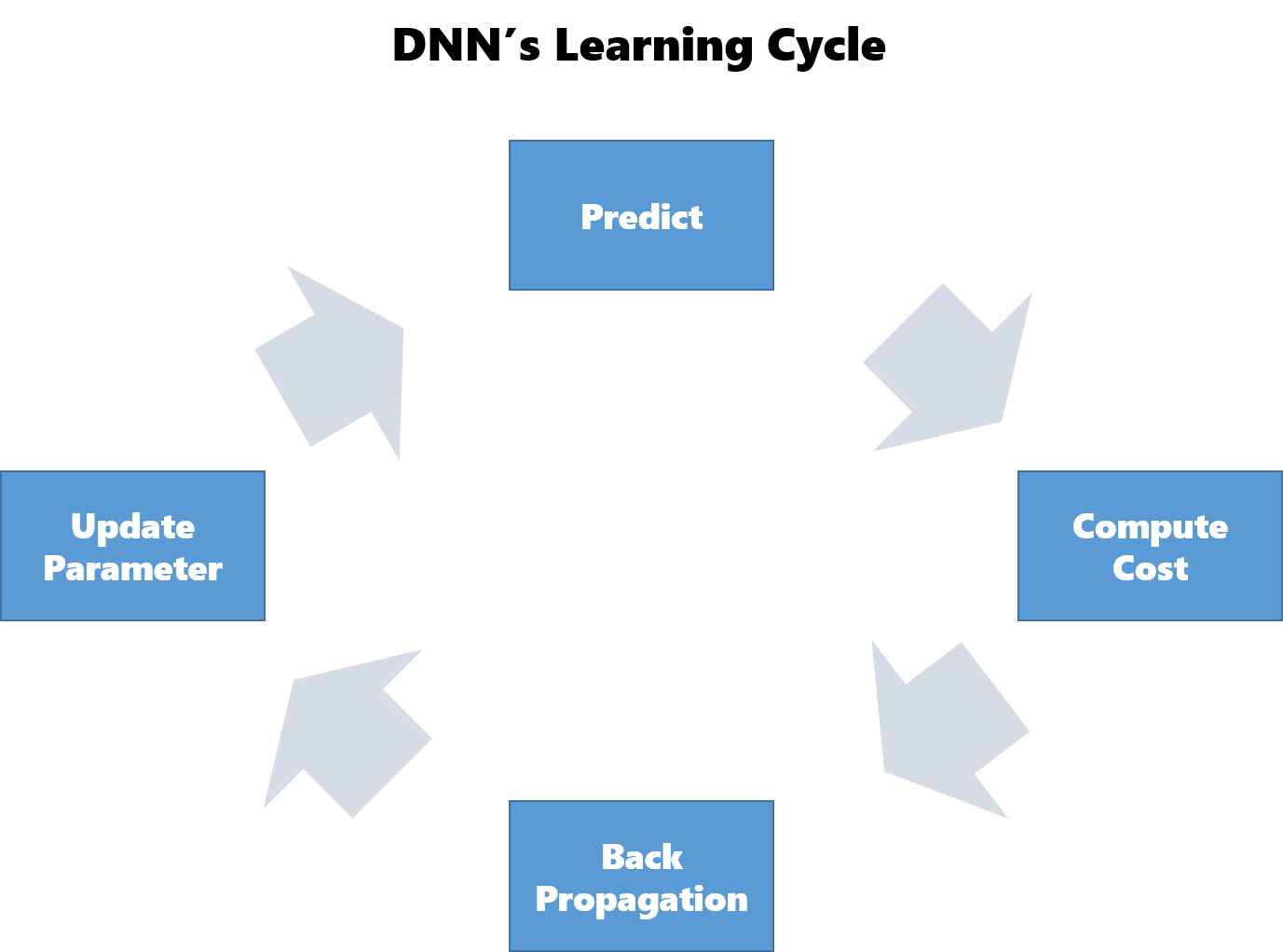
DNNでは以下の手順で学習を行います。2から5を繰り返し実行することで徐々にパラメータを最適化させていきます。
- パラメータの初期化
- 予測(Forward Propagation)
- 誤差を計算
- 誤差の逆伝播(Back Propagation)
- パラメータの更新
- 2に戻る
パラメータの初期化
今回は全てのレイヤでXivierの初期値を使って初期化しました。relu関数を使う場合にはHeの初期化を使うべきだそうですが、この辺の違いは正直まだよくわかっていないです。
Xivierの初期化
Xivierの初期化は、初期パラメータを平均$0$、標準偏差$\frac{1}{\sqrt{n}}$の正規分布からランダムに取り出します。標準正規分布から取り出す場合と比べ、狭い範囲から取り出すことで各層のアクティベーションが0と1付近に偏ることを防ぎ、勾配消失を起こりにくくします。詳細は「ゼロから作るDeepLearning」の182ページを参照してください。
4層あるので4層分のパラメータを初期化する必要があります。各層のレイヤ数をベクトル化したものを引数としてパラメータを返す関数を作成します。
def initialize_parameters(layers_dims):
np.random.seed(1)
parameters = {}
L = len(layers_dims)
for l in range(1, L):
parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1]) / np.sqrt(layers_dims[l-1])
parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
return parameters
予測(Forward Propagation)
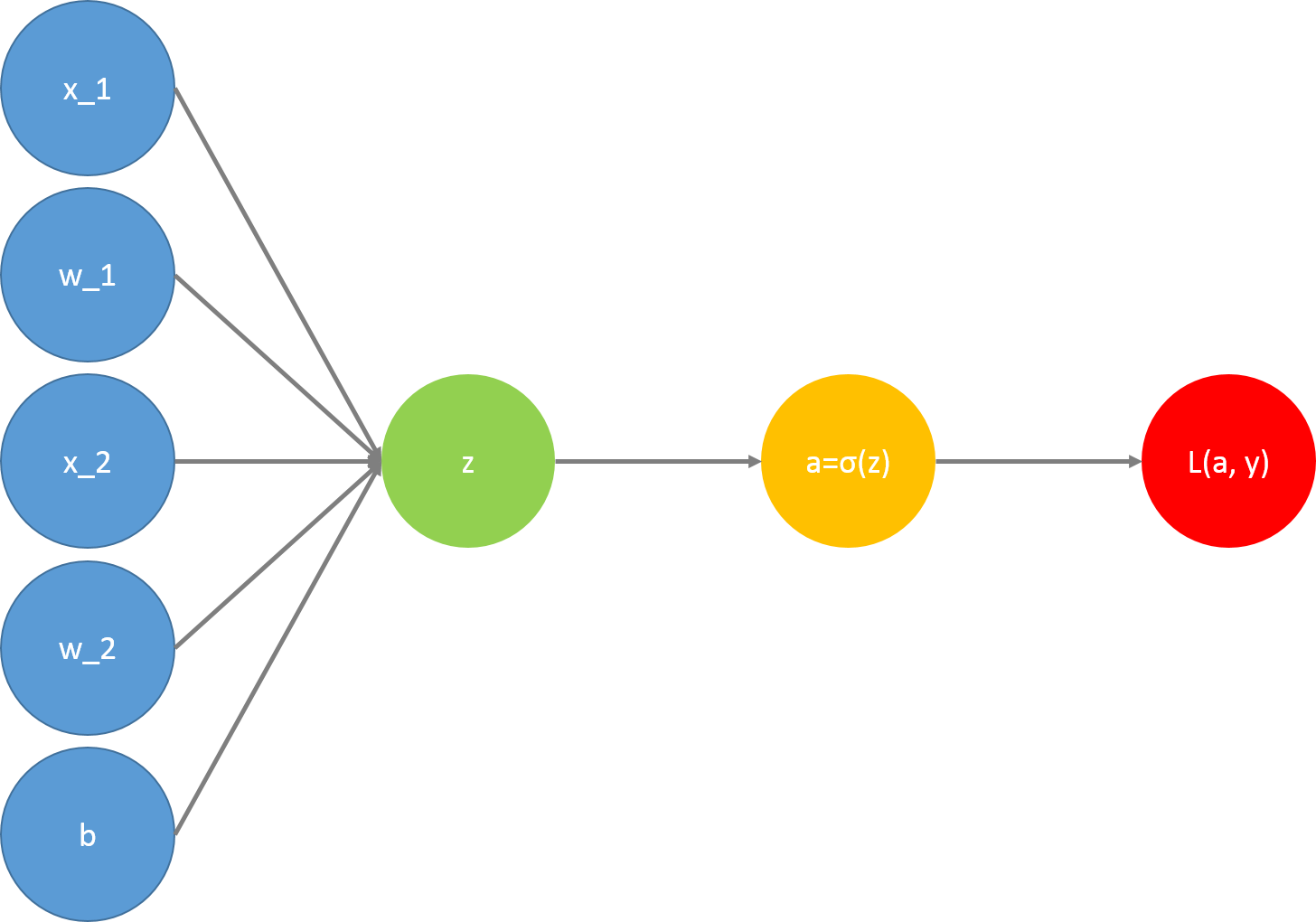
用意したパラメータを使って正解ラベルの予測を行います。全てのレイヤに対して以下の作業を行います。別の投稿で使用した図を流用しているのでコスト関数$L(a, y)$まで描画していますが、Forwad Propagationでは意識しなくてもよいので無視してください。
これを行うのに必要な関数は以下です。たまに出てくるcache、cachesはバックプロパゲーションの実装時に使用する変数です。
- 入力値XとパラメータWの内積+バイアス項を計算する関数
- activation関数(sigmoid(), relu())
- 1と2をまとめた関数
- 3をレイヤ数回繰り返す関数
入力値XとパラメータWの内積+バイアス項を計算する関数
def linear_forward(A, W, b):
Z = np.dot(W, A) + b
cache = (A, W, b)
return Z, cache
activation関数
def sigmoid(Z):
A = 1 / (1+np.exp(-Z))
cache = Z
return A, cache
def relu(Z):
A = np.maximum(0, Z)
cache = Z
return A, cache
1と2をまとめた関数
def linear_activation_forward(A_prev, W, b, activation):
if activation == 'relu':
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = relu(Z)
elif activation == 'sigmoid':
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = sigmoid(Z)
cache = (linear_cache, activation_cache)
return A, cache
3をレイヤ数繰り返す関数
def L_model_forward(X, parameters):
caches = []
A = X
L = len(parameters) // 2
for l in range(1, L):
A_prev = A
A, cache = linear_activation_forward(A_prev, parameters['W'+str(l)], parameters['b'+str(l)], activation='relu')
caches.append(cache)
AL, cache = linear_activation_forward(A, parameters['W'+str(L)], parameters['b'+str(L)], activation = 'sigmoid')
caches.append(cache)
return AL, caches
L_model_forwardを実行することで初期パラメータでの予測が行えます。
まとめ
今回はフォワードプロパゲーションまでの実装を行いました。次回はコストの計算を行いたいと思います。