アドベントカレンダーについて
この記事は東京大学工学部応用物理学系2学科(物工/計数) Advent Calendar 2020 の15日目の記事です.物理工学科・計数工学科の学生(や,院生や,OB/OGの方)が,毎日各々の関心ごとを記事にしています.リンクから他の記事もぜひご覧ください.
ガウシアンビームとは
まずはガウシアンビームについて解説しようと思います.光は電磁場の一種ですので,Maxwell方程式によって記述できます.角振動数$\omega$を持つ真空中の電磁場をMaxwell方程式に代入すれば以下のHelmholtz方程式が得られます.
$$(\Delta+k^2)\boldsymbol{E}(\boldsymbol{r},\omega)=0$$
ここで,$k=\omega/c$としました.これを満たす方程式として代表的なものは平面波や球面波があります.まずは$z$方向への平面波
$$\boldsymbol{E}(\boldsymbol{r})=\boldsymbol{E}_0e^{-ikz}$$
から出発しましょう.(光学の分野では波数の符号は負にとる慣習があるようです.空間Fourier変換で見栄えがいいらしいです.)ガウシアンビームではこれを拡張し,振幅 $\boldsymbol{E}_0$ に「ゆるやかな」 $\boldsymbol{r}$ 依存性を持たせ,$$ $$
$$\boldsymbol{E}(\boldsymbol{r})=\boldsymbol{E}_0(\boldsymbol{r})e^{-ikz}$$
という形の解を考えます.これをHelmholtz方程式に代入すれば,
$$\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}-2ik\frac{\partial}{\partial z}\right)\boldsymbol{E}_0(\boldsymbol{r})=0$$
となります.さらに$z$方向への変化が小さいと仮定すれば,$z$についての二階微分を落とすことができて,
$$ $$$$\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}-2ik\frac{\partial}{\partial z}\right)\boldsymbol{E}_0(\boldsymbol{r})=0$$
という形の方程式が得られます.これを近軸Helmholtz方程式といいます.
さらにMaxwell方程式の別の式
$$\nabla\cdot\boldsymbol{E}(\boldsymbol{r},\omega)=0$$
に$\boldsymbol{E}(\boldsymbol{r})=\boldsymbol{E}_0e^{-ikz}$を代入すると,
$$\frac{\partial E_{0x}}{\partial x}+\frac{\partial E_{0y}}{\partial y}+\frac{\partial E_{0z}}{\partial z}-ikE_{0z}=0$$
となりますが,ここで同様に$\frac{\partial E_{0z}}{\partial z}$を無視すれば,
$$E_{0z}=\frac{1}{ik}\left(\frac{\partial E_{0x}}{\partial x}+\frac{\partial E_{0y}}{\partial y}\right)$$
が得られます.これより,あるスカラー関数$\Psi(\boldsymbol{r})$を考え,それが近軸Helmholtz方程式の解であるとすれば,$$\boldsymbol{E}_1=\left(\Psi(\boldsymbol{r}),0,\frac{1}{ik}\frac{\partial \Psi(\boldsymbol{ r})}{\partial x}\right)$$
と,$$\boldsymbol{E}_2=\left(0,\Psi(\boldsymbol{r}),\frac{1}{ik}\frac{\partial \Psi(\boldsymbol{r})}{\partial y}\right)$$
は,ベクトルとして近軸Helmholtz方程式の解となっています.電磁場が$z$方向へ進んでいることと,$z$成分が十分小さいことを踏まえれば,この二つのベクトルを線形結合して近似的に電場を構成することができます.よって問題はこのスカラー関数$\Psi(\boldsymbol{r})$を求めることに帰着されます.ここで$r=\sqrt{x^2+y^2}$を導入し円筒座標系を導入すると,
$$\left(\frac{\partial^2}{\partial r^2}+\frac{1}{r}\frac{\partial}{\partial r}+\frac{1}{r^2}\frac{\partial^2}{\partial \theta^2}-2ik\frac{\partial}{\partial z}\right)\Psi(\boldsymbol{r})=0$$
が得られます.「ガウシアンビーム」とは,この方程式に対する$z$軸周りに回転対称かつ$r$方向にガウシアン関数の形の解のことを言います.すなわち,定数 $A_0$ を用いて以下の形を仮定します.
$$\Psi(\boldsymbol{r})=A_0\exp(S(z)r^2+T(z))$$
この式を円筒座標形における近軸Helmholtz方程式に代入すると,
$$\left(4S(z)^2r^2+4S(z)-2ik\left(r^2\frac{d S(z)}{d z}+\frac{d T(z)}{d z}\right)\right)A_0\exp(S(z)r^2+T(z))=0$$
$r^2$の項と$r^0$ の項で分けて考えると,
$$4S(z)^2-2ik\frac{d S(z)}{d z}=0$$
$$4S(z)-2ik\frac{d T(z)}{d z}=0$$
少々面倒ですが応用物理学魂で計算すると,この微分方程式の解が定数 $B_0$,$B_1$ を用いて以下のように表せます.
$$S(z)=-\frac{ik}{2(z+B_0)}$$
$$T(z)=-\ln(z+B_0)+B_1$$
これを$\Psi(\boldsymbol{r})$の式に代入すると,定数を$A$に吸収させて,
$$\Psi(\boldsymbol{r})=\frac{A}{z+B_0}\exp\left(-\frac{ik}{2(z+B_0)}r^2\right)$$
が得られます.最後に定数$B_0$について考察しましょう.動径方向にガウシアン関数の形の解を考えていますから,$B_0$が実数ですと$\exp$の項が減衰を示さず振動するため不適です.$z$は実数ですので,$B_0$の実部を$z$の原点の選び方に吸収させれば,$B_0$を純虚数に取ることができます.そこで,正の実数$z_0$を用いて,$B_0=iz_0$とおきましょう.これを代入すれば,再び定数をAに吸収させて
\begin{eqnarray*}
\Psi(\boldsymbol{r})&=&A\frac{z-iz_0}{z^2+z_0^2}\exp\left(-\frac{ikz}{z^2+z_0^2}\frac{r^2}{2}-\frac{kz_0}{z^2+z_0^2}\frac{r^2}{2}\right)\\
&=&A{\frac {w_{0}}{w(z)}}\exp \left({i\eta (z)-ik{\frac {r^{2}}{2R(z)}}-\frac {r^{2}}{w^{2}(z)}}\right)
\end{eqnarray*}
ここで,
$$R(z)=\frac{z^2+z_0^2}{z},\quad\eta(z)=\tan^{-1} \left(\frac{z}{z_0}\right),\quad w_0^2=\frac{2z_0}{k},\quad w^2(z)=\frac{2(z^2+z_0^2)}{kz_0}=\frac{\omega_0^2(z_0^2+z^2)}{z_0^2}$$
とおきました.$z$方向へ進む成分$e^{-ikz}$を復活させれば,所望のビームは,
$$\Psi(\boldsymbol{r})e^{-ikz}=A{\frac {w_{0}}{w(z)}}\exp \left({-ikz+i\eta (z)-ik{\frac {r^{2}}{2R(z)}}-\frac {r^{2}}{w^{2}(z)}}\right)$$となります.これが求めたかったガウシアンビームの表式です.先ほど導入した各パラメータについて物理的意味を考えると,$R(z)$は等位相面の曲率半径,$w_0$はビームウエスト径,$\eta(z)$はGuoy位相と言われる位相のズレ,$z$は ビームウエストの位置を$z=0$としたときの$z$座標, $z_0$はレイリーレンジというビームの広がりの大きさの指標に対応しています.
Guoy位相について考えてみると,
$$\eta(-\infty)=-\frac{\pi}{2},\quad\eta(\infty)=\frac{\pi}{2},\quad\eta(-z_0)=-\frac{\pi}{4},\quad\eta(z_0)=\frac{\pi}{4}$$ですから,$z$が$-\infty$から$\infty$に進む間に,平面からの寄与$-ikz$に加えてGuoy位相からの位相シフトが$\pi$だけ加わることになります.
ガウシアンビームは以下で定義されるビームパラメータ$q(z)$によって特徴付けられます.
$$\frac{1}{q(z)}=\frac{1}{R(z)}-\frac{2i}{k w^2(z)}$$
この$q(z)$を用いると,ガウシアンビームは
$$\Psi(\boldsymbol{r})e^{-ikz}=A{\frac {w_{0}}{w(z)}}\exp \left({-ikz+i\eta (z)-ik{\frac {r^{2}}{2q(z)}}}\right)$$
と書き換えられます.
ABCD行列
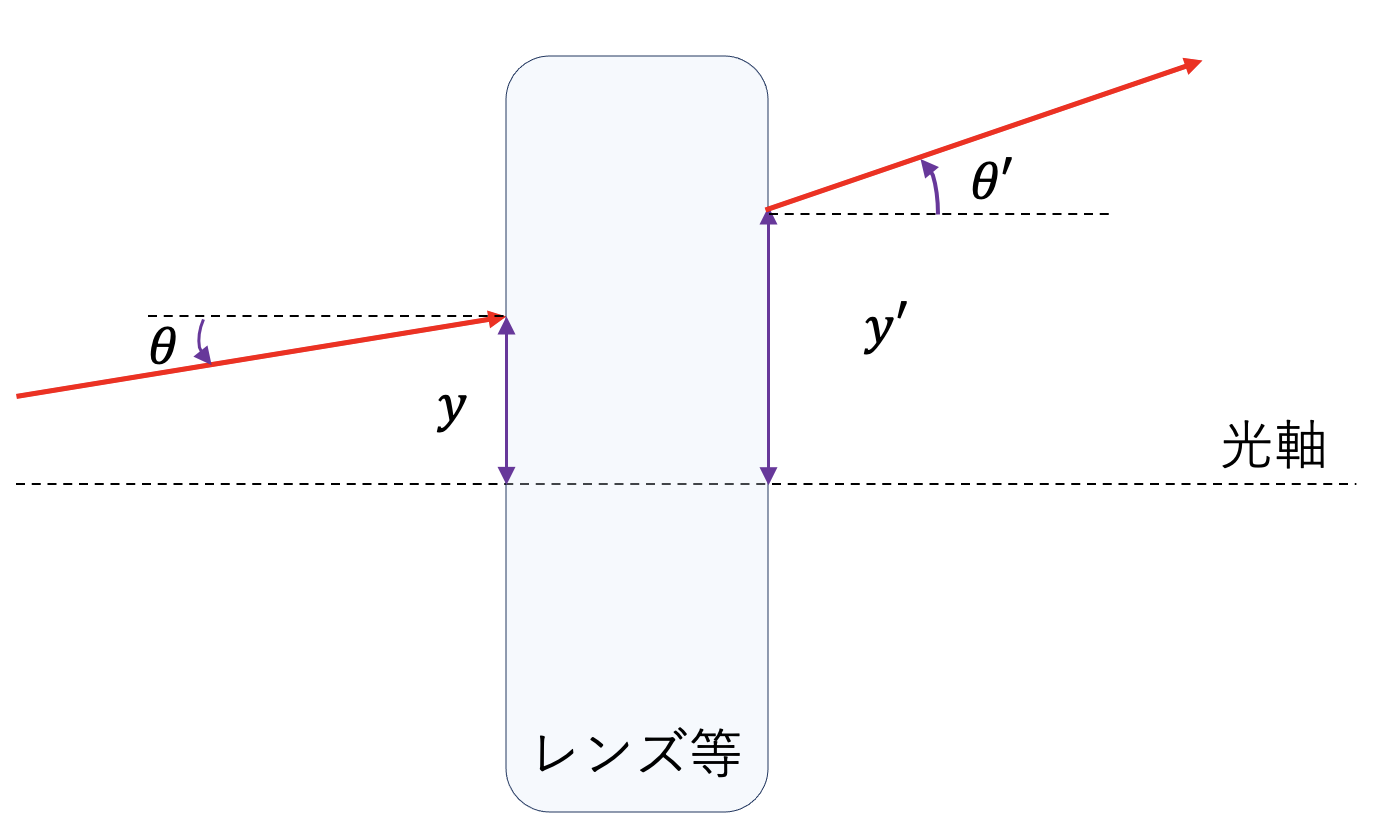
続いて,レンズなどの光学系の作用を考えましょう.まずは光学系に入射する光線を特徴付けるパラメータを考えます.光軸は$z$軸とし,それと垂直に $y$ 軸を定義したとき,光線が下図のように光軸からの角度 $\theta$ で光学系に座標 $y$ で入射したとします.$$ $$
これをパラメータとすれば,考えている光線はパラメータを並べたベクトルで$$ $$
\begin{pmatrix}
y \\
\theta
\end{pmatrix}
と特徴付けられます.この光線がある光学系に入射し,なんらかの作用を受け,
\begin{pmatrix}
y' \\
\theta'
\end{pmatrix}
と表されるような光線に変化したとします.これを元の縦ベクトルにある行列が作用した結果と捉えれば,光学系の作用と行列演算が対応づけられます.これをABCD行列と言います.
\begin{eqnarray*}
\begin{pmatrix}
y' \\
\theta'
\end{pmatrix}=\begin{pmatrix}
A & B \\
C & D
\end{pmatrix}\begin{pmatrix}
y \\
\theta
\end{pmatrix}
\end{eqnarray*}
近軸近似が成り立つ範囲,すなわち $\theta\ll1$となる範囲で,代表的なABCD行列を見てみましょう.
焦点距離 $f$のレンズは
$$ $$
\begin{pmatrix}
1 & 0 \\
-1/f & 1
\end{pmatrix}
距離$d$の並進は
\begin{pmatrix}
1 & d \\
0 & 1
\end{pmatrix}
屈折率$n_1$の物質から$n_2$の物質への入射は
$$ $$
\begin{pmatrix}
1 & 0 \\
0 & \frac{n_1}{n_2}
\end{pmatrix}
となります.ここで,屈折率$n$の媒質内で,
\begin{pmatrix}
y \\
\theta
\end{pmatrix}
を
\begin{pmatrix}
y \\
n\theta
\end{pmatrix}
と定義し直せば,屈折率の異なる物質への入射を表すABCD行列を単位行列で表すことができ,それ以外の行列に関しては形を変えないため,以後はこの定義を採用することにします.こうすることで上の三種類のABCD行列の行列式が1になります.嬉しい.
(なら最初からそちらで定義しろという話ですが,授業では最初の形で定義しており,また,定義変更により光学の体系における他の部分で矛盾が出る可能性もあるため,一応この定義は今後の議論だけのものと考えてください.)
この定義のもと,以降は行列式が1となるようなABCD行列を考えます.代表的なABCD行列は上の3種類のABCD行列の積に分解できるため,行列式は常に1となります.(任意のABCD行列でこの条件が成り立つかどうかは浅学につきわかりません.どなたか証明を知っている方はお教えください...)
以後スペースの都合上,行列計算があらわに出てこない限り$(y,n\theta)$のように横ベクトルで表記するとします.
ビームパラメータの伝搬
いよいよ本題です.あるABCD行列を持つ光学系にガウシアンビームを作用させると,どのような作用を受けるでしょうか.入射前のビームパラメータを$q_1$,透過したビームパラメータを$q_2$とすると,以下の関係式が成り立ちます.
$$ $$
$$q_2=\frac{Aq_1+B}{Cq_1+D}$$
この関係式を証明するのが今回の本題となります.ではいきましょう.
光学系が次のように配置されているとします.ここでは簡単のため$xy$平面を$y$方向のみで考えます.(二次元の場合も同じです.)光軸に$z$軸を取り,$z_1\le z \le z_2$の区間に光学系があります.$z\le z_1$の屈折率を $n_1$, $z\ge z_2$の屈折率を $n_2$ とします.$z$軸上に二点$P$と$P'$をとり,$P$ の座標を $(y,z)=(0,z_1-d_1),\quad P'$の座標を$(y,z)=(0,z_2+d_2)$としましょう.以下ではこの$P$と$P'$を通るような光を考えます.
ここで二つの経路を設けます.一つ目は最も単純な経路で,$z$軸にそって$P$と$P'$を通るようなものとし,これを経路1とおきます.
続いて,$P$を通過し,$z_1$から$(y_1,n_1\theta_1)$で光学系に入射し,ABCD行列の作用を受け$z_2$で$(y_2,n_2\theta_2)$となり,最終的に$P'$を通るような経路を経路2とします.
$$ $$
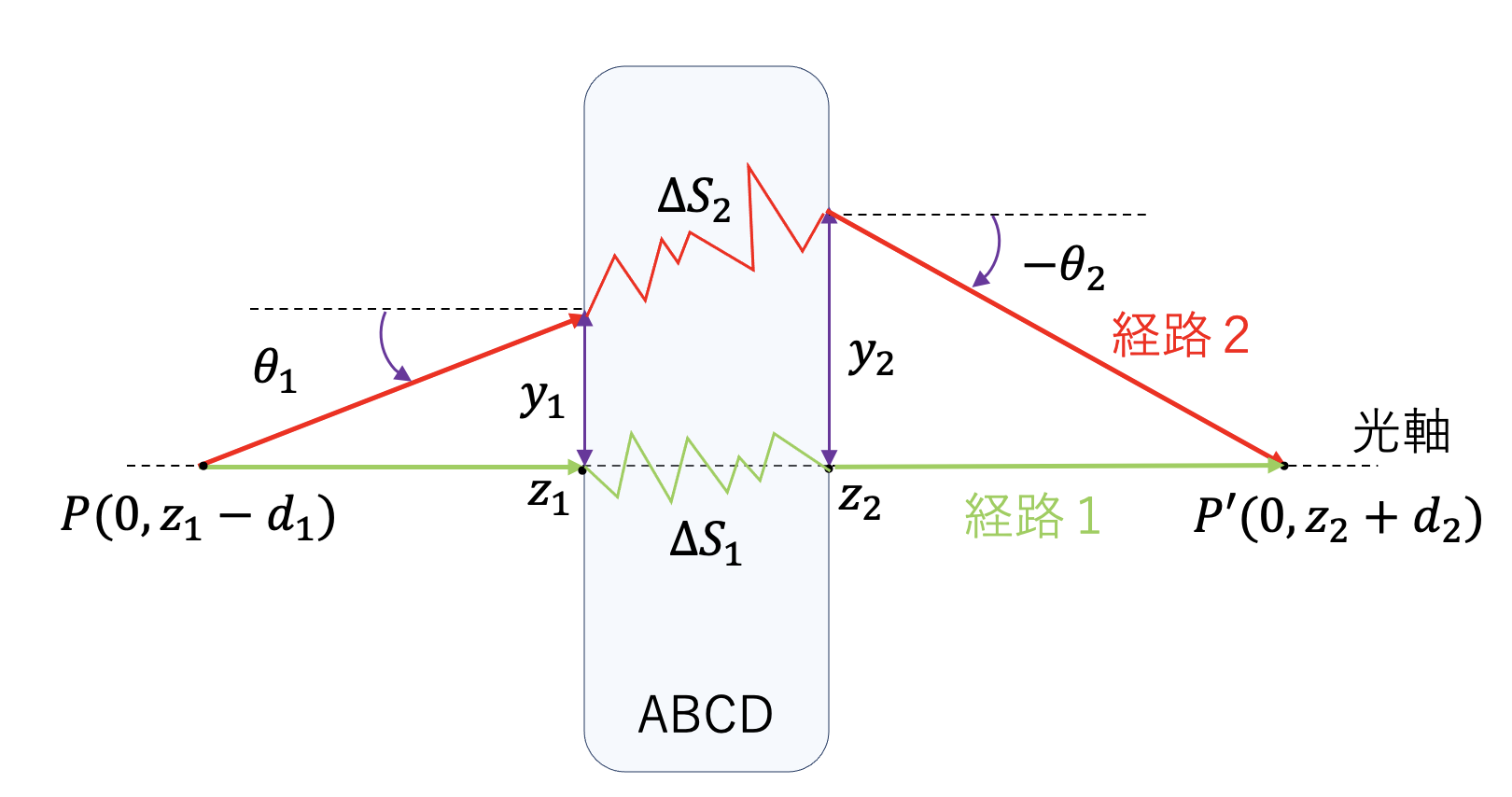
フェルマーの原理によると,「$P$と$P'$を通るあらゆる経路の内で光が実際に通る経路は光路長が最小となるもの」であるため,経路1の光路長$L_1$と経路2の光路長$L_2$は一致する必要があります.よって基準となる$L_1$に対して$L_2$を比較することで,経路$L_2$に関する情報が得られます.
$$ $$
まずは$L_1$について.$(y,z)=(0,z_1)$から$(y,z)=(0,z_2)$までの光路長を$\Delta S_1$とおきます.このとき,
$$L_1=n_1d_1+n_2d_2+\Delta S_1$$です.ここで,$\Delta S_1$は$y_1$や$y_2$に依存しないことに注意しましょう.
次に$L_2$について.$(y,z)=(y_1,z_1)$から$(y,z)=(y_2,z_2)$までの光路長を$\Delta S_2$とおきます.$P$から$(y,z)=(y_1,z_1)$までの光路長は近軸近似のもとで
$$n_1d_1+n_1\frac{y_1^2}{2d_1}$$となり,同様に$(y,z)=(y_2,z_2)$から$P'$までの光路長は
$$n_2d_2+n_2\frac{y_2^2}{2d_2}$$となります.よって結局
$$L_2=n_1d_1+n_1\frac{y_1^2}{2d_1}+n_2d_2+n_2\frac{y_2^2}{2d_2}+\Delta S_2$$
です.これを$L_1=L_2$に代入すれば,
$$\Delta S_2=\Delta S_1-n_1\frac{y_1^2}{2d_1}-n_2\frac{y_2^2}{2d_2}$$
が得られます.
続いて$\Delta S_2$をABCD行列を用いて表します.
$$y_2=Ay_1+Bn_1\theta_1$$
より,
$$n_1\theta_1=\frac{y_2-Ay_1}{B}$$
\begin{eqnarray*}
n_2\theta_2=Cy_1+Dn_1\theta_1&=&Cy_1+D\frac{y_2-Ay_1}{B}\\
&=&\frac{Dy_2-y_1}{B}\quad(\because AD-BC=1)
\end{eqnarray*}
さらに,近軸の範囲で,
$$\frac{y_1}{d_1}=\theta_1$$
より,
$$d_1=\frac{n_1By_1}{y_2-Ay_1}$$
同様に
$$\frac{y_2}{d_2}=-\theta_2$$
より
$$d_2=\frac{-n_2By_2}{Dy_2-y_1}$$
が得られます.ここで,$\theta_2$の符号は定義より負になります.これを$\Delta S_2$の式に代入すれば,
$$\Delta S_2=\Delta S_1+\frac{Ay_1^2-2y_1y_2+Dy_2^2}{2B}$$となります.
いよいよ最終段階です. $(y_2,z_2)$ におけるスカラー場 $\Psi_2(y_2,z_2)$ は,$(y_1,z_1)$におけるスカラー場$\Psi_1(y_1,z_1)$からの寄与を$y_1$で積分すれば得られます.ここで$(y_2,z_2)$における場は,$(y_1,z_1)$における場が光路長$\Delta S_2$を通過する間に,減衰と位相変化を受けたものの重ね合わせとなります.
$$ $$
近軸を考えているため,減衰の効果は$z_2-z_1$のみによるとみなせば,$y_1$と$y_2$は位相のみに影響します.求めたいものはビームパラメータですから,$\exp$の中身だけを考えて,残りは$y_1$と$y_2$には依存しない定数$C_0$にまとめると,
$$ $$
\begin{eqnarray*}
&&\Psi_2(y_2,z_2)\sim \frac{C_0}{ z_2-z_1}\int_{-\infty}^{\infty}\Psi_1(y_1,z_1)\exp(-ik\Delta S_2)dy_1 \\
&=&\frac{C_0\exp(-ik\Delta S_1)}{ z_2-z_1}\int_{-\infty}^{\infty}\Psi_1(y_1,z_1)\exp\left(-ik\frac{Ay_1^2-2y_1y_2+Dy_2^2}{2B}\right)dy_1\\
&=&\frac{C_0\exp(-ik\Delta S_1)}{z_2-z_1}A{\frac {w_{0}}{w(z_1)}}\exp \left({i\eta (z_1)}\right) \int_{-\infty}^{\infty}\exp\left(\frac{-iky_1^2}{2q_1}-ik\frac{Ay_1^2-2y_1y_2+Dy_2^2}{2B}\right)dy_1\\
&\propto&\exp\left(-iky_2^2\left(\frac{D}{2B}-\frac{1}{2B^2(1/q_1+A/B)}\right)\right)\\
\end{eqnarray*}
最後の式変形はガウス積分を用い,ビームパラメータを考える上で関係しない部分は省略しました.光学系を通過後のビームパラメータを$q_2$とすると,$$\Psi_2(y_2,z_2)\propto \exp(-ik\frac{y_2^2}{2q_2})$$より,$$\frac{D}{2B}-\frac{1}{2B^2(1/q_1+A/B)}=\frac{1}{2q_2}$$
これを$AD-BC=1$を用いて変形すれば,所望の式$$q_2=\frac{Aq_1+B}{Cq_1+D}$$が得られます.めでたしめでたし.
参考文献
[1]: 大野木哲也・田中耕一郎 著, 「電磁気学Ⅱ 物質中の電磁気学」,基幹講座 物理学, 東京図書,2017.
[2]: Yariv, Amnon (1989). Quantum Electronics (3rd ed.). Wiley.
[3]: Eugene Hecht (2016). Optics, Global Edition. Pearson Education Limited.
[4]: 砂川重信 著,「理論電磁気学」,紀伊國屋書店,1999.