今年 10月に Google が量子超越性を達成したとのニュースがあったことは皆さんの記憶に新しいことと思います。
以下素人解説ですが、公開されている実験データを眺めながら論文の概要を追ってみます。基本的に量子コンピューターに詳しくない方や、量子コンピュータを勉強し始めた方を念頭において書いています。
私の説明には間違いもあると思いますので、さらに興味のある方は Qmediaさんのわかりやすい解説 もぜひご覧ください。これを読んで興味を持たれた方は、元の論文 も長くないので英語に抵抗がなければぜひ一読されることをお勧めします。
そもそも量子超越性って?
量子コンピューターは、ある種の問題のサイズを大きくすると古典コンピューターより速く解けるだろうと考えられています。しかし、現在の量子コンピューターはまだまだ黎明期で、大きな問題を解くことができません。
そのため実在する量子コンピューターでできる計算は、だいたいスパコンでもできてしまうと考えられています。そこで、現在の量子コンピュータでも可能で、スパコンでもできないことを実行してみせよう、というのがここでの量子超越性の考え方だと思います1。
そのためには、
- 現在の量子コンピューターで実行可能でスパコンではできない問題を探して、
- 実際に実行して、結果が正しいことを検証する
必要があります。
結局何をやったの?
Google の量子コンピューター研究者は、53量子ビットが使用できる量子コンピュータで、ランダムな回路(プログラム)を実行した結果を観測しました。
基本的に量子コンピューターの回路を一度実行すると、ランダムな値が出力されます。ただし値が返される確率(確率分布)は回路に依存します。例えば、53量子ビットの計算結果は、 1度の実行ごとに 0 から 2^53-1 までのどれかの数値が返されますが、ある回路は 42 (0x00101010) しか返さないかもしれません。別の回路では全ての値を同じ確率で返すこともあり得ます2。
一般に、あるランダムな回路を繰り返し実行した場合、回路に特有の確率分布が観測できます。
実際に Google の論文で公開されているデータを見てみましょう。12量子ビットのあるランダム回路の出力はこんな感じで 500,000 サンプル(500,000 行)あります。
$ head n12_m14/measurements_n12_m14_s0_e0_pEFGH.txt
100001000001
000101111011
011000101100
111001100001
001110110000
010010010011
011000111000
101011010001
110000100101
000001010000
流石にこれではよくわからないので、観測された値のヒストグラムを描いてみましょう。x 軸が観測された値(bit 列を 10進数にしたもの)で、y 軸が観測された回数です。x 軸方向に $2^{12} = 4096$ サンプルあり、表示されているピクセル数の方が少ないので、グラフの形は完全ではないことに注意が必要です。

ランダム回路だけにノイズみたいですね。論文の中では、ランダム回路の出力を「laser speckle」に例えていますがなんとなく雰囲気はわかります。
一方、このランダム回路の結果の確率分布を古典コンピューターで計算で再現するのはかなり計算力が必要で、おおむね回路の大きさ(量子ビット数または回路の長さ)に対して指数関数的に時間がかかると考えられています。
しかし、量子コンピューターは誤差が許容範囲ならば回路を実行することで簡単に「計算」できますので、スパコンでも計算できない大きさの回路が実行できれば量子超越!ということです。
先ほどの2項目に当てはめてみます。
- 現在の量子コンピューターで実行可能でスパコンではできない問題を探して、
-> 「大きなランダム回路のアウトプットを作る」ことが「スパコンではできない問題」になります3 - 実際に実行して、結果が正しいことを検証する
-> 実行はできても、検証は難しいです。次に説明します。
結果をどうやって検証するの?
実機の結果には誤差が含まれます。そのため先ほどのヒストグラムもどれだけ正確かを確認する必要があります。
理論値との比較
先ほどのような 12量子ビット程度の大きさですと、ノートPC でも簡単にシミュレートできますので理論値との比較が可能です。先ほどのデータに対応する回路も公開されていますので、シミュレーションして確率を計算してみましょう。

うーん、実験結果と似てる…のかな?意外と誤差があるんですね…
人間がヒストグラムを見ながら感覚的に判断するわけには行きませんので、論文では、XEB (cross entropy benchmark) fidelity という数値で実験の忠実度を評価しています。機械学習などでも使用される cross entropy という値を使用して、以下の式で fidelity (忠実度)を定義しているようです4。
\begin{aligned}
F_{xeb} = 2^N {\left\langle P(x_i) \right\rangle} -1
\end{aligned}
ここで $N$ は量子ビット数、 $P(x_i)$ は、$x_i$ という値が観測される(シミュレーションで得られる)確率で、${\left\langle \right\rangle}$ はサンプル全体での平均を意味しています。python でそれっぽいコードを書くとこんな感じでしょうか?
from statistics import mean
N = 12 # 量子ビット数
p = [..] # シミュレーションで計算された各値の確率
experiment_data = [0b100001000001, 0b000101111011...] # 実験結果の配列
f_xeb = 2**N * mean(p[x] for x in experiment_data) - 1
この式は単純ですが、なんらかの前提があるようで正直よくわかりません(ごめんなさい)。実験結果が完全にノイズで全ての値を同じ確率で観測すると、確率の平均( mean(..) 部分)はサンプル数が大きい極限で $1/2^N$ になると思われますので、$F_{xeb}$ は 0になります。シミュレーション結果の確率分布がある性質をもつ場合は、実験結果が理論値と一致すると $1$ になる(または近くなる)ようです。ざっくりいうと、1に近いと誤差が少なくて、0だとダメダメです。
実際に上記のデータで $F_{xeb}$ を計算すると、 $F_{xeb} = 0.38$ という結果が出てきます。結構低く見えますね。
論文ではゲート一つあたりのエラー率は 0.1% 程度と非常に誤差が非常に低いですが、回路が使用しているゲート数が 1,500 程度と多いので、粗い見積もりで、$ 0.999^{1500} = 0.22$ 程度になってしまいます。これは乱暴な見積もりですが、大きな回路を実行するには、個々のゲートにものすごく高い精度が要求されることがわかります。
理論値が作れない場合
さて、もともと量子超越を目指していたのですから、スパコンでも計算できないサイズの回路を実行したいのでした。ここで矛盾にぶち当たります。
スパコンでシミュレーションできない回路(量子超越を実証する回路)は $F_{xeb}$ が計算できないため直接検証ができません。
なんらかの工夫が必要です。論文ではシミュレーションできない大きい回路の $F_{xeb}$ を、「同じサイズだけど簡単な回路」の $F_{xeb}$ を計算することで見積もっています。
具体的には以下の2つの方法で「同じサイズだけど簡単な回路」を用意しています。
- 量子ビット間の結合を減らす。 full、elided、patch の3パターンを用意します。
- 量子ビット間の結合パターンを変える。「ABCDCDAB」、「EFGH」の2パターンを用意します。
full > elided > patch の順、ABCDCDAB > EFGH の順に複雑です。
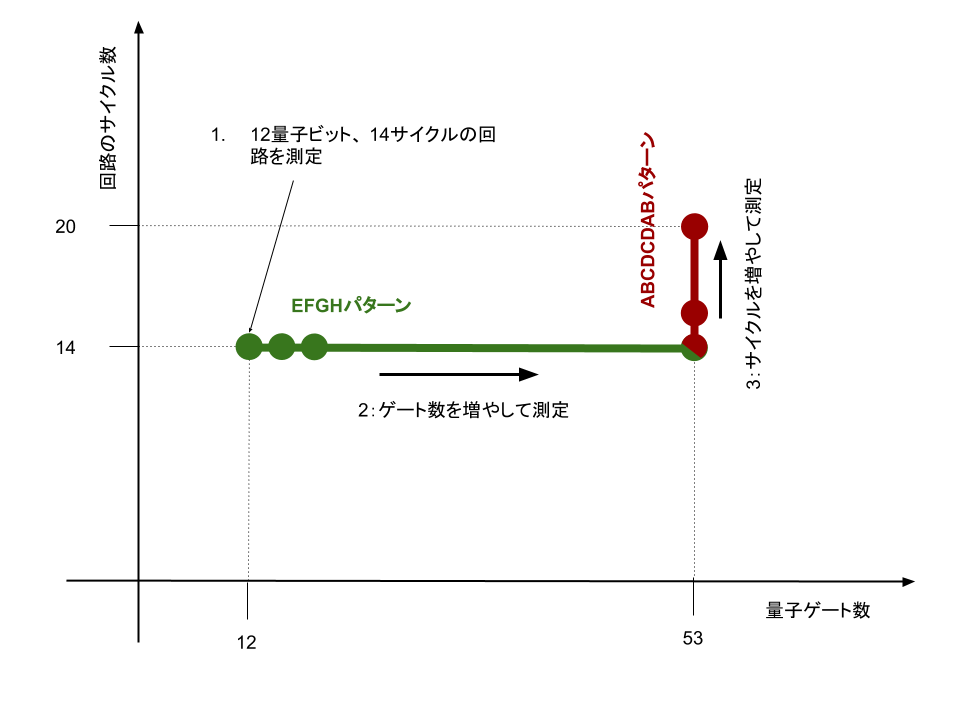
だいぶ詳細を省略しましたが、これで実験の内容が理解できます。論文では以下の流れで量子超越領域の $F_{xeb}$ を見積もっています。
- 簡単な EFGH パターンを使い、12量子ビット、長さ14のランダム回路を、それぞれ full、elided、patch で計測します。それぞれの回路の $F_{xeb}$ を比較し、full 回路の $F_{xeb}$ が elided や patch 回路の $F_{xeb}$で見積もれることを確認します。
- 量子ビット数を増やしながら 1, 2 を繰り返して、53量子ビットまで計測します。EFGHパターンの場合はスパコンでも53量子ビットがシミュレーションできるようです。理論的には量子ビット数を大きくすると指数関数的に $F_{xeb}$ が小さくなっていくことが予想されています。ここでも patch、 elided の $F_{xeb}$ をもとに fullの $F_{xeb}$ が見積もれることを確認します。
- 今度は、ABCDCDAB パターンの53量子ビット回路で長さを変えながら full、elided、patch 回路を観測します。この場合、patch、elided はシミュレーションできますが、full はスパコンでは計算できないので、full の $F_{xeb}$ は patch、 elided から見積もります。$F_{xeb}$ が許容範囲なら量子超越が達成できたことになります。
この結果は論文の Fig.4 にまとまっていますが、その前に実際の回路を見てみましょう。
ランダム回路
Google が実験で使った量子ビットは、2次元の平面上に実装されています。(Supplementary information for Quantum supremacy using a programmable superconducting processor Fig S27 を引用)

円が量子ビットで、量子ビットをつなぐ線は実線点線とも量子ビット同士を結合するためのチャネルです。いわゆるコントロールゲートを作るために使用します。図の通り、量子ビットの位置にによって結合可能な量子ビットが決まっていて、量子ビット1番は 2、4、5、8番の量子ビットとのみコントロールゲートを使用できます。
実験では、1番の量子ビットから順番に使用したようです。先ほどの 12ビットの回路は、1から12までの長方形の部分を使用したことになります。
さて、ここからはやや詳細な部分です。実際のランダム回路をみてみましょう。ランダムと言ってもめちゃくちゃにゲートをつなげているわけではなく、量子ビットの位置関係を考慮した「いい感じ」の回路を使用しています。
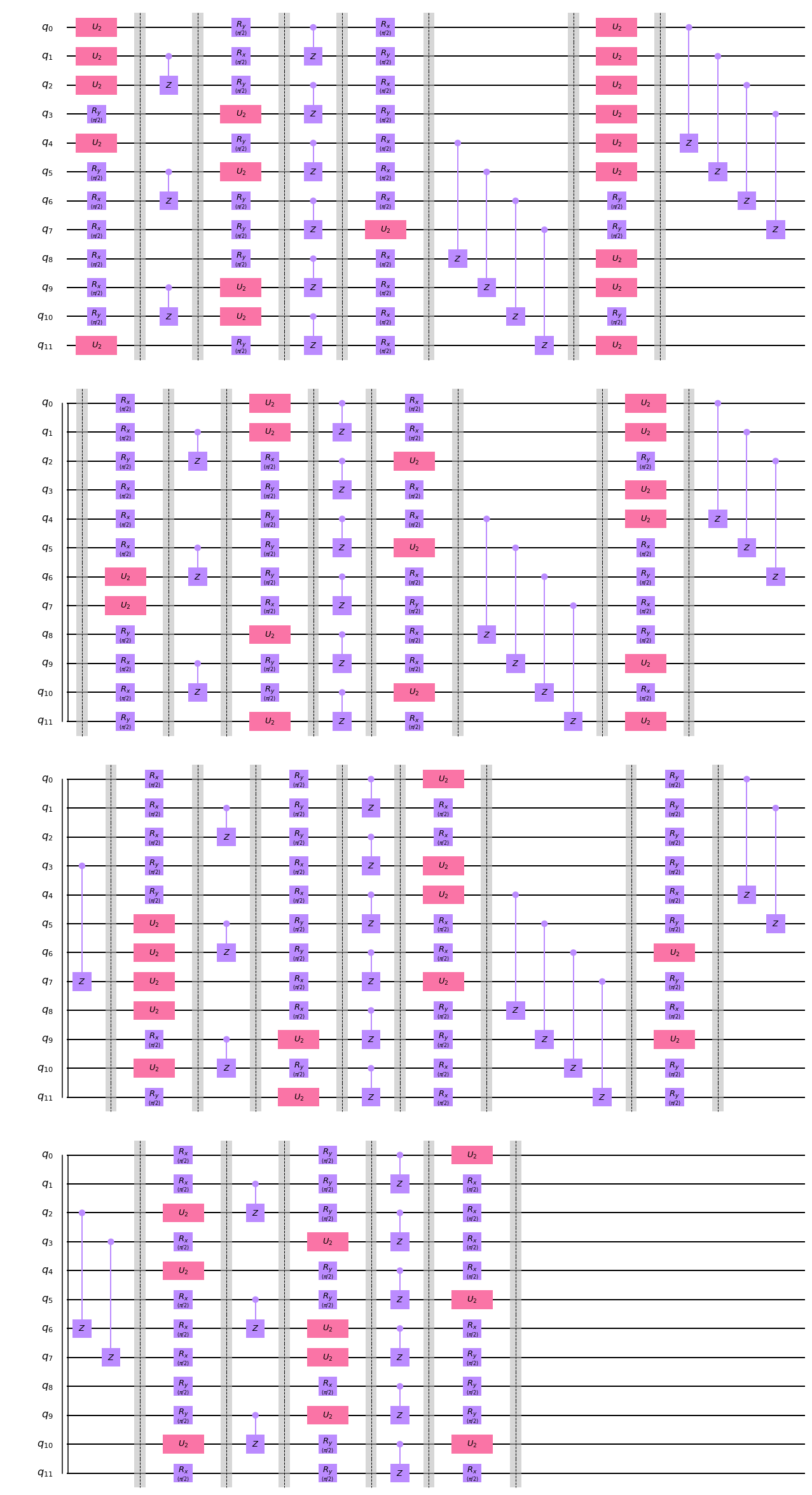
先ほどシミュレーションで使用した回路を簡略化して qiskit の circuit_drawer で描画してみました。
長いので折り返されています。一番上の左がスタートで、右端まで行ったら一段下の左に続きます。
遠目に見るとパターンを感じ取れると思います。以下の繰り返しです。
- 各量子ビットに Rx, Ry, W(図では U2) のゲートをランダムに選んで実行
- 位置が隣り合った量子ビット同士をカップリングさせる(図では CZ)。物理的な位置なので回路の位置とは異なりますが、線が引かれているもの同士は物理的に隣り合っています。
- 1,2を繰り返す
- 最後にもう一度、各量子ビットにランダムなゲートを実行する
1と4の部分でランダム性を導入して、2の部分で量子ビットを「混ぜ合わせて」います。この構造を使って、1と4の部分を別の組み合わせにするといくらでもランダムな回路が作れるわけです。この回路では、1と2を14回繰り返した後、4を実行して終わりにしていますが、繰り返し回数を長くすることも可能です。
ちなみに、図では CZゲートを表示しましたが、実際には fSim ゲートというやや複雑な2量子ビットゲートを使用しています。
さて、このランダム回路ですが、シミュレーションが難しくなる要因はカップリング部分(fSim ゲート)です。先ほどの話に戻りますが、このカップリングを変更することでシミュレーション可能な回路を用意したのでした。回路と量子ビットの配置図を見た後ならそれぞれが理解できます。
- patch : 2次元平面図の赤い点線で、量子ビットを完全に切り離し、回路中でこの赤線部分に当たる fSim ゲートを実行しません。こうすると実質的に27量子ビットと26量子ビットの2つの小さな量子コンピュータになるので、それぞれを別にシミュレーションできます。
- elided : 2次元平面図の赤い点線の量子ビットを回論の前半では切り離し後半でのみ使用します。
ABCDCDAB、EFGHは Supplementary paper の Fig S25 に具体的な図がありますので、引用します。

ABCDCDAB の順で fSim ゲートを実行すると、EFGHEFGH で実行する時よりそれぞれのゲートがより量子もつれが速く広がるようです。
「量子超越」のグラフ
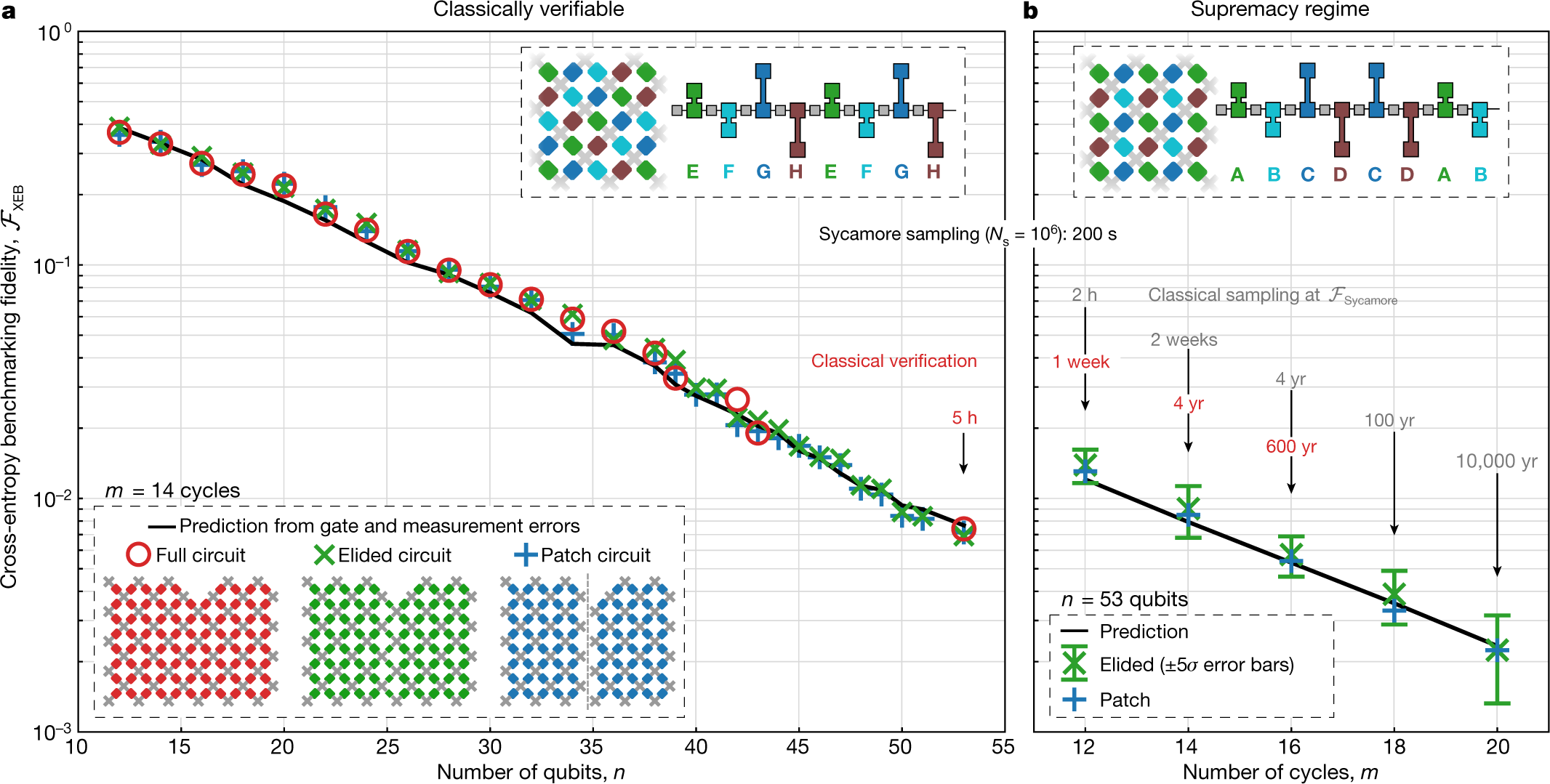
さて、回路の説明をしたところで最後に論文のグラフを眺めてみましょう。(元論文 Fig 4 を引用)
左のグラフは、EFGH の簡単なカップリングパターンを14サイクル実行した結果です。縦軸が $F_{xeb}$ で横軸が量子ビット数です。縦軸が log スケールなので、量子ビット数を増やすと指数関数的に $F_{xeb}$ が下がっていく観測結果になっています。これは理論的に予想していたものと一致している結果と言えそうです。また、full、elided、patch どれも差がなく、簡略化した回路で $F_{xeb}$ を見積もることが正当化できそうです。
右のグラフは、量子ビットを53に固定して ABCDCDAB の複雑なカップリングパターンを実行したものです。シミュレーションはfull では実行できず、elided と patch のみが可能です。そちらでの $F_{xeb}$ の結果から、full の回路も同じ程度の $F_{xeb}$ を持つだろう、少なくとも 0.001 よりは大きいだろう、と結論づけています。
終わりに
さて、ざっくりと論文の流れを追ってみました。ご存知の方も多いかと思いますが、「量子超越」という部分について IBM から反論の論文も出ていますし、理論の専門家からの批判もあります。「量子超越」が確定するにはもう少し時間がかかるかもしれません。
ただ、Supplementary Information を読んだ感想は、量子超越よりも実際に量子コンピュータを作って、地道に検証・調整をして、理論と整合するデータをとるという泥臭いプロセスの記述に迫力があります。例えば、論文でもさらっと触れられていますが、fSim ゲートを適用する際にエラーを減らすためフェーズを調整しているようで、実際の回路でもこの泥臭い部分が垣間見れますので、以下に cirq で書かれた回路の冒頭部分を引用します。コメントは私が入れたものです。
CIRCUIT = cirq.Circuit(moments=[
# randomゲートを各量子ビットに実行します
cirq.Moment(operations=[
cirq.PhasedXPowGate(phase_exponent=0.25,
exponent=0.5).on(cirq.GridQubit(3, 3)),
cirq.PhasedXPowGate(phase_exponent=0.25,
exponent=0.5).on(cirq.GridQubit(3, 4)),
cirq.PhasedXPowGate(phase_exponent=0.25,
exponent=0.5).on(cirq.GridQubit(3, 5)),
(cirq.Y**0.5).on(cirq.GridQubit(3, 6)),
cirq.PhasedXPowGate(phase_exponent=0.25,
exponent=0.5).on(cirq.GridQubit(4, 3)),
(cirq.Y**0.5).on(cirq.GridQubit(4, 4)),
(cirq.X**0.5).on(cirq.GridQubit(4, 5)),
(cirq.X**0.5).on(cirq.GridQubit(4, 6)),
(cirq.X**0.5).on(cirq.GridQubit(5, 3)),
(cirq.X**0.5).on(cirq.GridQubit(5, 4)),
(cirq.Y**0.5).on(cirq.GridQubit(5, 5)),
cirq.PhasedXPowGate(phase_exponent=0.25,
exponent=0.5).on(cirq.GridQubit(5, 6)),
]),
# fSimの前に位相を調整してるようです
cirq.Moment(operations=[
cirq.Rz(np.pi * 0.2767373377033284).on(cirq.GridQubit(3, 4)),
cirq.Rz(np.pi * -0.18492941569567625).on(cirq.GridQubit(3, 5)),
cirq.Rz(np.pi * -1.00125113388313).on(cirq.GridQubit(4, 4)),
cirq.Rz(np.pi * 1.1224546746752684).on(cirq.GridQubit(4, 5)),
cirq.Rz(np.pi * -0.33113463396189063).on(cirq.GridQubit(5, 4)),
cirq.Rz(np.pi * 0.40440704518468423).on(cirq.GridQubit(5, 5)),
]),
# fSimを実行します
cirq.Moment(operations=[
cirq.FSimGate(theta=1.5862983338115253, phi=0.5200148508319427).on(
cirq.GridQubit(3, 4), cirq.GridQubit(3, 5)),
cirq.FSimGate(theta=1.5289739216684795, phi=0.5055240639761313).on(
cirq.GridQubit(4, 4), cirq.GridQubit(4, 5)),
cirq.FSimGate(theta=1.5346175385256955, phi=0.5131039467233695).on(
cirq.GridQubit(5, 4), cirq.GridQubit(5, 5)),
]),
# fSim実行後の位相を再度調整してるようです
cirq.Moment(operations=[
cirq.Rz(np.pi * -0.6722145774944012).on(cirq.GridQubit(3, 4)),
cirq.Rz(np.pi * 0.7640224995020534).on(cirq.GridQubit(3, 5)),
cirq.Rz(np.pi * 0.7990757781248072).on(cirq.GridQubit(4, 4)),
cirq.Rz(np.pi * -0.6778722373326689).on(cirq.GridQubit(4, 5)),
cirq.Rz(np.pi * 0.049341949396894985).on(cirq.GridQubit(5, 4)),
cirq.Rz(np.pi * 0.02393046182589869).on(cirq.GridQubit(5, 5)),
]),
上記が、12量子ビットの1サイクル分です。どうでしょうか?このハードコードされたマジックナンバーの壁!53量子ビットの場合は、この独自パラメータが 53 並ぶわけです。
これらの数値一つ一つが地道に積み上げた観測結果から導き出されたものだと考えると、なかなかエモい量子回路だなーと思う次第です。
長くなってしまいましたが、ここまでお読みいただきありがとうございました。間違いや勘違いも多いとは思いますが、コメントなどでご指摘いただけると助かります。
2020年も量子コンピューターに多くの進展があることを願っています。皆様も良い年末を!
参考文献
- Quantum supremacy using a programmable superconducting processor
- Supplementary information for "Quantum supremacy using a programmable superconducting processor"
-
この定義は多分に私の解釈が入っています。量子情報理論では量子計算が古典計算より強いということを理論的に証明する文脈で量子スプレマシーという言葉を使っていますので、量子超越性(量子スプレマシー)という言葉の使い方が専門家の間でも微妙に異なる気もしています。興味のある方はQmediaさんの「「量子計算機が古典計算機より優れている」とはどういうことか」もご覧ください。 ↩
-
素因数分解のような一般的な意味での「計算」をする場合、出来るだけ一つの値に確率が収束するのが望ましいです。そのためには確率が一つの値に収束するような回路をデザインする必要があります。 ↩
-
ここ、微妙ですがヒストグラムを作ろうとすると量子コンピュータでも $2^N$ に比例する観測回数が必要になってしまい、古典との優位性がありません。ですので、「ある確率分布に従うランダム値を返す」という乱数発生器みたいな計算が目標になります。 ↩
-
cross entropy をご存知の方はこの式をみて違和感を感じたかもしれません。通常の cross entropy $\sum_{x,y} -log(p(x))q(y)$ は一方の確率に log を使用しますが、ここでは log を使用しない linear cross entropy というものを使用しているようです。 ↩