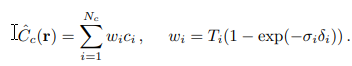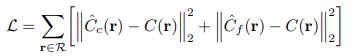最近の3D分野の技術の一部をざっと読んでいきます。
・・・のつもりで書こうと思ったら、画像生成の分野の話でした。
CVPR2021のBestPaperに選ばれたという「GIRAFFE」を中心に、
「NERF」「GRAF」「GAN」と読んでみます。読むだけで組みません。
式の意味とか掘り下げていないので、どんなことできるか程度に読みます。
NERF
git -> https://github.com/bmild/nerf
paper -> https://arxiv.org/pdf/2003.08934.pdf
一言で言うなら、
たくさんの画像から↓みたいなの出力するぜ!!という技術。
概要
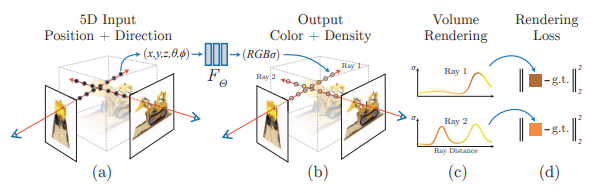
入力として
3D位置(x,y,z)、撮影者から見たときの2次元の角度情報を与えて、
出力として
RGBの色情報とvolume densityという密度を出力します。
さて、ここで言う密度とは、イメージ的には空間的な広さを表現した数値です。
例えば、夏の青空に照らされた景色をみると遠くのものほど、物体が青っぽくなります。
画像的に言えば、物体の不透明度が下がり、背景の青が徐々に強くなっていく状態です。
この状態を再現することで空間的な広さを演出する方法をボリュームレンダリングと呼び、
ここで出力された密度はボリュームレンダリングに利用されます。
そして最終的な出力としては、ボリュームレンダリングにより、
「それっぽさ」がました画像が作成されます。
もう少し読む
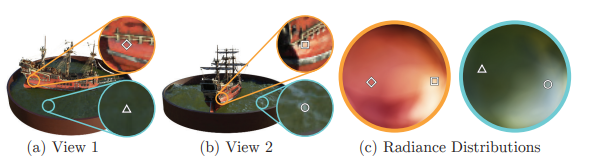
入力として与えられる画像情報はスパースな情報です。
例えば図の(a)と(b)のように、撮影されたシーンの間は連続していません。
サンプルの学習データを見ると、系20個程度のデータしか有りません。
上の方の動画のような結果を得るには、間のシーンの補完が必要です。

ここでもう一度図を見ます。(上)
画像上では同じ位置・同じ箇所を示していながら、光の影響で刻一刻と色味が変わります。
画像間の間のシーンを補完しようと思ったら、各ポイントの変化分を推定しないといけません。
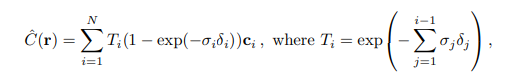
なので、微小変化分を積分でガチャッと合わせてやることで色を推定します。(5.1の内容)
各ポイントに対して上記のような処理を行うわけですが、
画像が重ならないところとか遮蔽物に隠れて見えないところは使わないほうがよくね?
という考えのもと、全てのポイントではなく、そのうちのいくつかを「粗く」サンプリングして、
処理をかけているらしいです。
そのネットワークを司るのが、$C_c$という粗いネットワーク。
そして更に、「細かい」ネットワーク$C_f$も作成します。
「細かい」ネットワークは、$C_c$の結果と、別のサンプリング数で実行した結果も加えるらしいです。
そんでもって、こいつらのネットワークが出力した結果(色情報)と
正解の結果との誤差の二乗が最小化されるように最適化することで学習を行います。
アルゴリズムとしてはAdamを使っているようです。
GIRAFFE
git -> https://github.com/autonomousvision/giraffe
paper -> http://www.cvlibs.net/publications/Niemeyer2021CVPR.pdf
一言で言うなら、
自動でリアルな画像を生成するぜ!しかも位置とか背景とかも自在に出力するし、物体の位置も自由自在!
物体そのものを変化させることもできるぜ!!!という技術。すげー。

概要
フォトリアリスティック。photorealistic。
最近の映画は3Dがあまりに進化しすぎて、現実特別つかない域にまで到達してます。
でもこういうのって、ものすごいお金かかるんですよね。
近頃はGAN (参考:https://innolab.jp/work/gan/5200 ) を使って
フォトリアリスティックな画像を自動生成できたりして、
フォトリアリスティックの業界に少しずつ変化が訪れてきています。
本稿では、画像にうつる各物体のスケール・移動・回転を自在にコントロールし、
加えて、形状・外観も変化させながらシーンに移る物体を自在にコントロールします。
また、従来技術では一枚のシーン全体を変化させますが(NERFとか)、
本技術では、シーンのうち特定の物体だけを動かすなどの制御が可能です。
物体
Neural Radiance Fields(NERF)
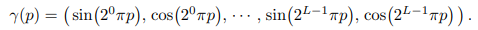
NERFの論文の5.1を読み直します。
曰く、低次元の三次元座標$x$と、視線方向を司る二次元情報$d$を入力としてそのまま使うと、
最終的な出力は高周波(?)の情報が無視されてしまい、一部情報が失われてしまうようです。
この問題に対して、位置と視線の五次元の情報をそのまま使わず、
変換(位置エンコード)して使うことtで、より高次元の特徴の入力として取り扱うらしい。
NERFは最終的に上述の「色(RGB)」と「密度」を出力し、出力関数は下記のように表されます。
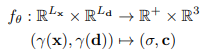
$f$は多層パーセプトロンて表される関数です。$f_\theta$でいうところの$\theta$とは、
多層パーセプトロンの重みとかバイアスとかのパラメータのことを指しています。
GIRAFFEではNERFを導入して、入力情報として位置・視線方向を扱います。
Generative Neural Feature Fields:(GRAF)
https://arxiv.org/pdf/2007.02442.pdf
GENFの論文のP5のところを読んでみます。
NERFでは、位置と視線方向を入力としてあたえることで、画像の位置と視線を自在にコントロールしました。
GRAFでは、これに形状・外観を追加で入力することで、形状・外観もコントロールします。
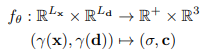
これがNERFの出力関数(MLP)。
入力として位置と視線方向の情報を入れいています。
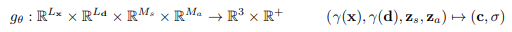
そしてGENFでは、形状の情報$z_s$、外観の情報$z_a$の情報を追加しています。
NERFでは、位置と視線方向をモデル化することで画像の位置視点をコントロールし、動画のような映像を出力しました。
GENFでは、形状と外観を追加したことで、形状と外観を操作できるようになりました。
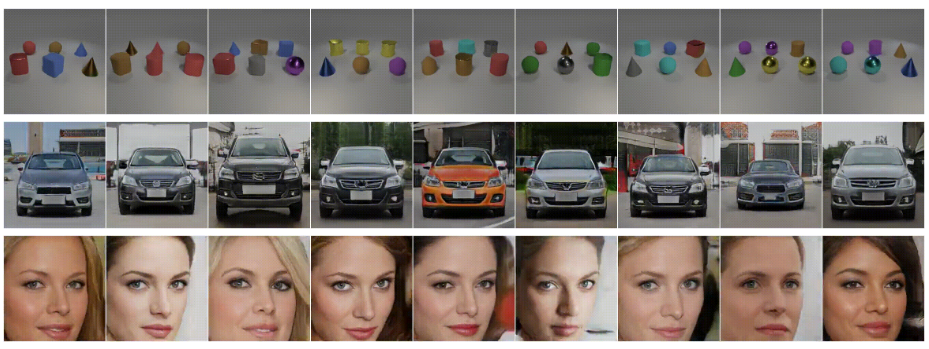
↑gitのリンク先ではこれが動画になっています。刻一刻と画像がかわっていくことがわかります。
このように、形状と外観を制御することが可能です。
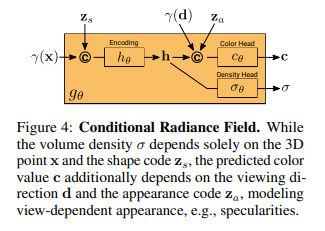
さて、出力される色情報と密度のイメージは図のようになります。
密度$\sigma_{\theta}$は位置と外観情報を結合したものが出力され、
色情報$c_{\theta}$は位置と外観情報、そして視線方向の情報と形状から出力されます。

なおGRAFでは色情報$c_{\theta}$を上式のように表されますが、
本稿では、$R^{M_f}$として表現しています。色情報はGRAFの導入により、特徴$f$として表されます。
物体ごとの表現
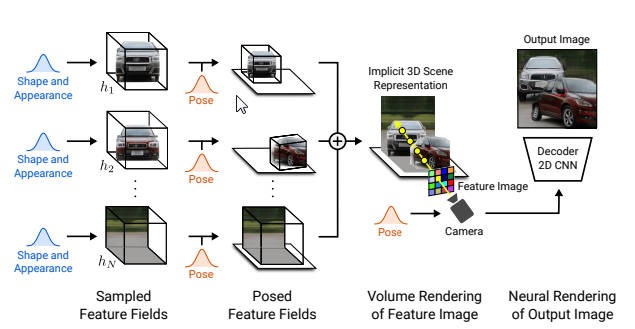
GIRAFFEは物体ごとのモデルを想定しています。
具体的なイメージとしては、
上記画像のようにそれぞれの車とそれぞれの背景が別々に入力/出力されます。
この構造により、図の赤い車のように赤い車だけ回転させるなどの制御を可能としています。
NERF/GRAFでは、
画像全体を対象にしているためシーン全体に対してしか操作できませんでした。
GIRAFFEでは各物体をそれぞれ制御することで、全体のシーンを自在に制御できるようになりました。
加えて、GIRAFFEでは物体のスケール、移動、回転を行うことが可能です。
なので、GRAFにおける入力としては、
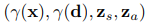
これが、スケール、移動、回転によるアフィン変換が行われるので
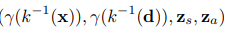
このような入力になります。
シーン構成
シーンが構成される形成過程としては
様々ある物体をそれぞれアフィン変換で変形させながら位置・視線方向・形状・外観を作成したあと、
それぞれの物体を1つのシーンに統合します。
合成演算子
(8)式の通り。N個のモデルを足して平均を求めます。
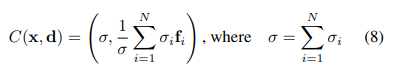
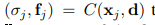
これが、最終的に一枚のシーンに合計された出力結果となります。
この出力結果には、各物体のモデルの位置形状その他諸々を反映された結果が収納されています。
シーン作成
3Dボリュームレンダリング
ここまでの説明により、
各物体モデルの密度$\sigma$と色位置形状その他諸々の特徴を司る$f$を式で表しました。
そして、各物体は1つのシーンに統合されるため、
最終的な1つのシーンとして反映される$\sigma$と$f$は、合成演算子で表されました。
そしてシーン全体の特徴画像$f$は下式で表されます。
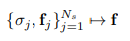
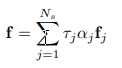
特徴画像は低解像度であえて出力するそうです。
2Dレンダリング
低解像度の画像をアップサンプリングしていきます。
$\pi^{neural}$により、最終的な出力画像$I \in R^{HxWx3}$を得ます。
$\pi^{neural}$は畳み込みニューラルネットワークです。