素数判定いろいろ - シンプルな判定と、素数の分布

数学好きのエンジニアしてます @srtk86 です。本日の日付 1213 は素数です。

素数かどうかを判定するアルゴリズムについて色々見てみたので、その話をしようと思います。

動機・目的

最近、以下の記事が投稿されて話題になりました。
2が現れる素数 - INTEGERS

216桁の素数で、しかも18*12の形に並べ替えると、0の中に「2」が浮かび上がってくるビジュアル系素数の話です。眺めていると幸運が訪れそうですね。

その後、確率的な素数判定などを用いた検証の結果、「確かに珍しいけど、どうやら他にもこういった数はありそう」 とのことが見えてきています。例えば以下のような記事に詳しいです。
2が現れる素数が奇跡だという人に物申す

上の記事でも使われている openssl prime などは、内部でミラー・ラビン素数判定法と呼ばれるアルゴリズムを使っていて、かなりの精度で高速に素数判定を行うことができるそうです。
私も名前自体は聞いたことがあったのですが、どういった原理なのかきちんと確認したことがないなと思い、この機会に調べてみることにしました。

また、精度がかなり高いために十二分に実用的なのですが、個人的には、確実に素数だと言える方が嬉しいんですよね。100%素数であることと99.99%素数であることは心情としては違うわけで、決定的な判定を簡単には諦めたくないわけです。
そこで調べてみると、素数判定を確実に実施する方法として「AKS素数判定法」というものが存在することが分かったので、実際にプログラムを作成してその実用性を検証したりもしていました。
その結果、実用的ではないことも見えてきたのでw そのあたりの失敗も晒していこうかと思っています。

目次

シンプルな素数判定と、素数の分布 - 今ここ！
フェルマーテスト・ミラーラビン素数判定法
AKS素数判定法

実行環境

Python 3 が実行できる環境であることが条件です。（Python 2 は文法が異なるところがあるため実行できない可能性があります）
私は、MacOS上にPython3.6.3をインストール後、関連ライブラリをpipでinstallして実行しています。

素数の定義とシンプルな判定

まずは、素数の定義を確認します。

「素数とは、1とその数自身以外に正の約数を持たない、1より大きい整数」

素数の定義から単純に考えると、1とその数自身以外で割り切れないことを確認すれば、素数かどうかを判定できます。以下のような手順になります。

• n を判定したい数とする
• 2 から n - 1 までで n を割ってみる
  • もしどこかで割り切れたら n は合成数
• 最後まで割り切れなかったら n は素数

Pythonで記述すると以下のようになります。（print内の「PRIME」は素数、「composite」は合成数です。今後も時折出てきます）

n = 1213
for p in range(2, n):
    if n % p == 0:
        print(str(n) + ' is composite.')
        return
print(str(n) + ' is PRIME!!')

試行回数を減らした判定

これは、より効率よく書くことができます。
30を例にとって考えてみます。以下の数は全て30の約数です。

30 =  1 * 30
      2 * 15
      3 * 10
      5 *  6

眺めてみると、左側の数 (1, 2, 3, 5) と右側の数 (6, 10, 15, 30) はセットになっていて、ちょうど $\sqrt{30} \fallingdotseq 5.47722$ を境に、それより小さい数が左側、大きい数が右側のグループに入ります。素数かどうかの確認は $\sqrt{30}$ 以下の数で割れば十分です。

実際、整数 $n$ に対して、$\sqrt{n}$ 以上の約数が存在する場合、それを $a$ とすると、

\frac{n}{a} \leq \frac{n}{\sqrt{n}} = \sqrt{n}

も $n$ の約数になるので、素数の判定には $\sqrt{n}$ までを確認すれば十分です。
プログラムに反映するとこんな感じになります。

simple_prime_test.py

import math

def is_prime(n):
    if n == 1: return False

    for k in range(2, int(math.sqrt(n)) + 1):
        if n % k == 0:
            return False

    return True

素数の分布を示す「素数定理」

せっかくなので、これを活用して少し素数と戯れてみます。題材として「素数定理」を取り上げます。

「素数定理」とは、素数の分布に関する以下の有名な定理です。今から225年前にガウスがたったの15歳で予想したとされており、のち1896年に解決されています。

素数定理
自然数 $n$ までに現れる素数の個数を $\pi (n)$ とするとき、以下の近似式が成り立つ。

\pi (x) \sim \frac{x}{\ln{x}}

これは、「素数の個数が右辺の簡単な計算式で近似できる」というものです。一見なんの秩序もなさそうな素数の分布にこんな綺麗な性質があるなんて、本当に驚きです...！

この近似を使うと、特定の範囲における素数の個数・割合を推測することができます。
冒頭の記事にあげた「216桁」の場合、

• 216桁までの素数の個数: $10^{216} \div \ln{10^{216}} \fallingdotseq 2.010622601 \times 10^{213}$ 程度
• 215桁までの素数の個数: $10^{215} \div \ln{10^{215}} \fallingdotseq 2.019974334 \times 10^{212}$ 程度

なので、上の数から下の数を引いた値

$1.80862516796 \times 10^{213}$

が、「ちょうど216桁」の素数の個数と予想されます。割合にすると

$1.80862516796 \times 10^{213} \div (10^{216} - 10^{215}) \fallingdotseq 0.002009583 \fallingdotseq 0.2%$

ぐらいの割合で出現することになります。「500個のうち1個」程度なので、幸運なのは間違いないですね！

素数定理を感じる

先ほどの素数判定を使って、実際に素数定理の示す近似の様子を見てみることにします。
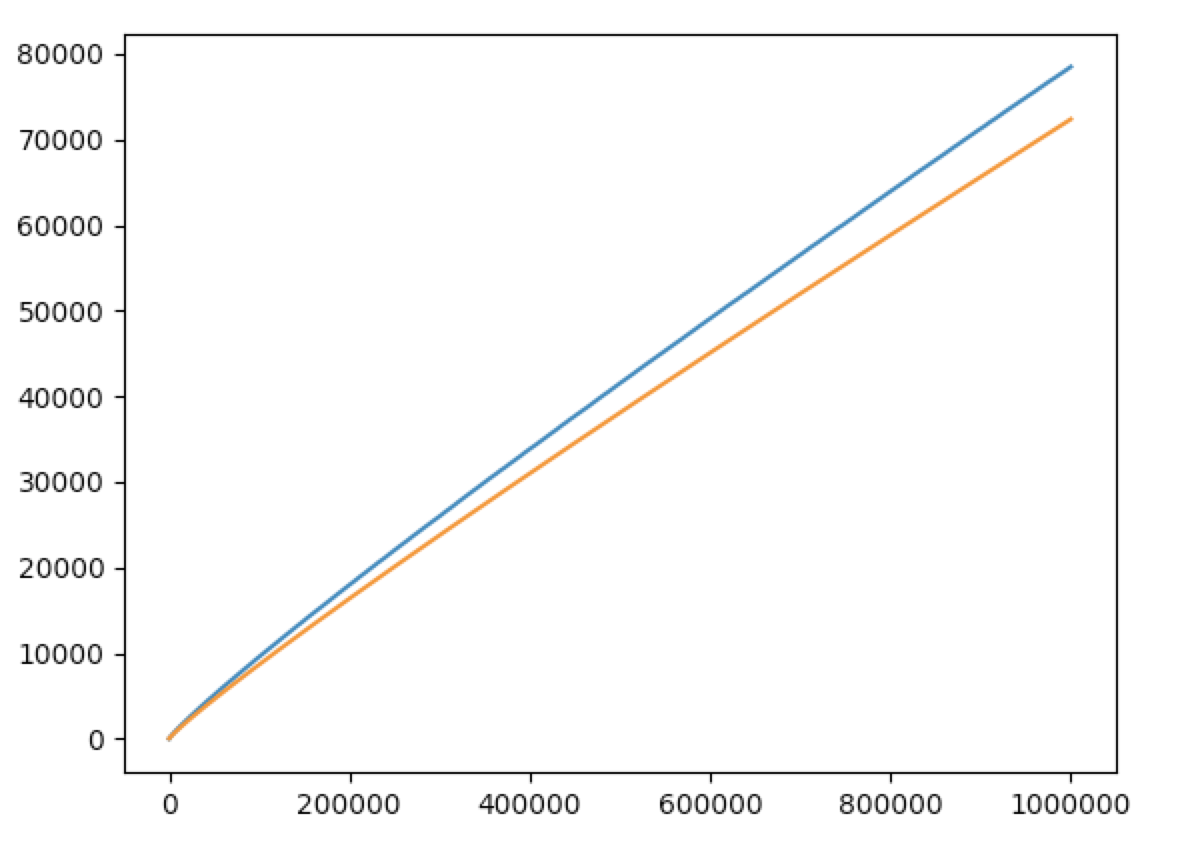
2から100万までの範囲で素数判定を行い、素数であればインクリメントすることで、素数の個数の座標をとっていきます。グラフ表現にはPythonのライブラリであるmatplotlibを用いることにします。（pipなどでインストールする必要があります）

simple_prime_test_graph.py

import simple_prime_test as simple
import math
import matplotlib.pyplot as plt

x1, y1 = [], []  # y = pi(x) (xまでの素数の個数) の座標群
x2, y2 = [], []  # y = x / log(x) の座標群
pi = 0

for n in range(2, 1000001):
    if simple.is_prime(n):
        pi += 1

    x1.append(n)
    y1.append(pi)

    x2.append(n)
    y2.append(n / math.log(n))

plt.plot(x1, y1)
plt.plot(x2, y2)
plt.show()

出力結果は以下のようになります。（オレンジが $\pi (x)$, 青が $\frac{x}{\ln{x}}$）

比率のグラフも出してみると、割合がどこかへ収束に向かっていそうな様子がより鮮明に見えてきます。（1に近い方向へ向かっているのも分かります）

simple_prime_test_ratio_graph.py

import simple_prime_test as simple
import math
import matplotlib.pyplot as plt

x1, y1 = [], []
pi = 0

for n in range(2, 1000001):
    if simple.is_prime(n):
        pi += 1

    if n % 100 == 0:
        x1.append(n)
        y1.append(n / (math.log(n) * pi))

plt.plot(x1, y1)
plt.show()

これだけの操作で素数定理をちょっぴり体感できるなんて、いい時代に生まれたものです。