OpenSeesPyによる建築構造解析の基礎1

このページに掲載されている内容によって生じた損失や損害に対して一切責任を負いません．
もしコードの誤りなどありましたら連絡ください．

OpenSeesPyとは

OpenSeesPyはPythonで構造解析や応答解析ができるライブラリです．

1. インストール

インストールはいくつか方法があり，詳しくはhttps://openseespydoc.readthedocs.io/en/latest/src/pypiwin.html に書かれています．コマンドプロンプトで次を実行すればインストールできます．

py -m pip install openseespy

モジュールのインポートは次のコードでできます．

import openseespy.opensees as ops

2. 例題

今回は次の静定構造物の構造解析の例題をもとに使い方を解説します．

2.0 問題

下の図のような節点0が固定端のL字のフレームの節点2に垂直下向きに$10\mathrm{N}$(図の$\mathrm{kN}\rightarrow \mathrm{N}$)の荷重が作用している．

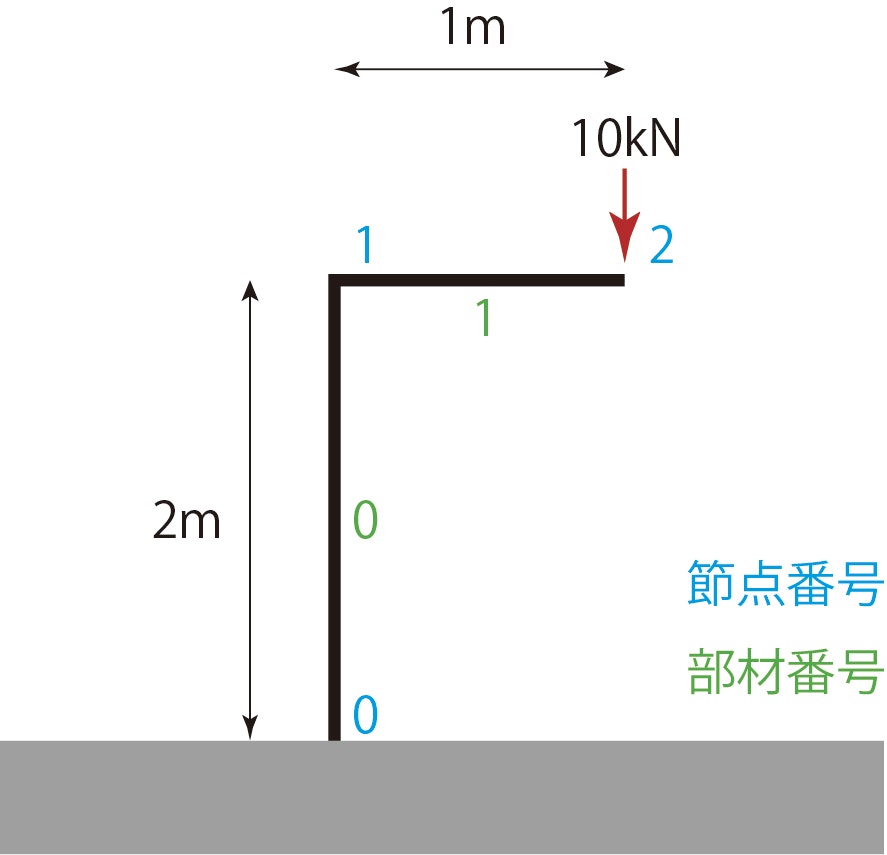
2.1 解析の流れ

OpenSeesPyの構造解析のプログラムは次の順序で記述します．

1. 解析モデルの設定
2. 節点座標の設定
3. 固定されている節点の境界条件の設定
4. 材料を定義
5. トラス部材の断面積と材料を定義
6. 外力を設定
7. 解析の実行
   以下ではこの順に書き方を解説します．

2.1.1 初期化

まず解析の初期化をします．OpenSeesPyは前回の解析モデルがOpenSees上に残っているとエラーが出てしまうことがあります．そこで解析をかける際には初期化をする必要があります．

# 初期化
ops.wipe()

2.1.2 解析モデルの設定

構造解析するモデルの存在する次元と接点の自由度を設定します．設定には，

# モデルの設定
ndm = 2 # 次元
ndf = 3 # 節点の自由度
ops.model('basic', '-ndm', ndm, '-ndf', ndf = ndm*(ndm+1)/2)

というメソッドを用います．それぞれの引数の内容は以下の通りです．
'basic'はおまじないのようなものです．特に気にしなくて大丈夫．(というか僕も理解していないです)
'-ndm', ndm, '-ndf', ndf = ndm*(ndm+1/2)の部分は次元と自由度を設定します．
次元-ndmは最大$x, y, z$の$3$次元で，節点の自由度-ndfは$x, y, z$方向の変位に加えて各方向の回転の合計$6$自由度考えられます．ndfを特に指定しないと，その次元の空間内の節点の取りうる自由度の最大値が設定されます．
今回の問題は座標系が$xy$平面上のndm=2次元で，節点の自由度が$xy$と$z$軸周りの回転の計ndf=3次元です．

2.1.3 節点の番号と座標の設定

ここでは節点の設定をします．節点の設定はops.node()でできます．
引数は次の通りです．

ops.node(nodeTag, *crds, '-ndf', ndf, '-mass', *mass, '-disp', *disp, '-vel', *vel, '-accel', *accel)

nodeTagは節点の番号，crdsは節点の座標，ndfは節点の自由度，massは節点の質量，velはノードの速度，accelはノードの加速度です．今回はとりあえずnodeTagとcrdsさえ把握していれば大丈夫です．次のコードで今回の問題の節点の番号と座標を設定しましょう．

p0 = [0.0, 0.0] # 節点0の座標
p1 = [0.0, 2.0] # 節点1の座標
p2 = [1.0, 2.0] # 節点2の座標
ops.node(0, *p0)
ops.node(1, *p1)
ops.node(2, *p2)

2.1.4 境界条件の設定

節点の境界条件(ピン，ピンローラ―，固定端等)の設定をします．これにはops.fix(nodeTag, *constrValues)メソッドを用います．nodeTagは節点の番号，*constrValuesは拘束条件です．自由度の大きさの長さの整数の配列で，0が拘束なし，1が拘束ありを意味します．
今回の問題では節点$0$のみに$x, y, R_z$方向に拘束かけているので，次のコードでできます．

# 境界条件
const0 = [1, 1, 1]
ops.fix(0, *const0)

2.1.5 柱梁の座標変換方法の設定

ここは少し発展的な内容になると思うので，難しかったら読み飛ばしてもらっておまじないだと思ってもらって大丈夫です．部材の座標系とグローバルな座標系の変換補法を定義します．変換方法によって，P-Delta効果を考慮したりしなかったりします．ここでは特にP-Delta効果は考慮せずに座標の線形変換をします．

# geotrans
ops.geomTransf('Linear', 0)

2.1.6 部材の定義

部材の定義には
ops.element('eletype', eleTag, *eleNodes, *eleArgs)
を用います．eleTypeは部材のタイプを表す文字列(str)で，'Truss', 'elasticBeamColumn'など様々な部材が用意されています．ここでは弾性の柱梁をモデル化するのでeleType = 'elasticBeamColumn'を使用します．eleTagは部材の番号(int)で*eleNodesは部材が結ぶ節点の番号の配列です．*eleArgsにはそのタイプの部材の定義に必要な定数の値の配列を入れます．'elasticBeamColumn'ではeleArgs = [A, E, Iz, crdTag]を入れてやります．

# 部材の定義
A = 5.0 # 断面積
E = 3000 # ヤング率
Iz = 2 # 断面二次モーメント
ops.element('elasticBeamColumn', 0, *[0, 1], A, E, Iz, 0)
ops.element('elasticBeamColumn', 1, *[1, 2], A, E, Iz, 0)

2.1.7 解析条件の設定と解析の実行

ここまでで構造物の設定は終了です．ここからは解析に必要な設定と解析の実行をします．今回の解析は次のコードで実行できます．

# define and run analysis 

# create SOE
ops.system("BandSPD")

# create DOF number
ops.numberer("Plain")

# create constraint handler
ops.constraints("Plain")

# create integrator
ops.integrator("LoadControl", 1.0)

# create algorithm
ops.algorithm("Linear")

# create analysis object
ops.analysis("Static")

# perform the analysis
ops.analyze(1)

解析結果として部材に働く力を表示します．ops.basicForce(eleTag)メソッドを用いて部材力を標準出力できます．

今回はここで終わりです．最後に今回の解析に使用したコードをまとめて示します．

import openseespy.opensees as ops

# 初期化
ops.wipe()
# 解析モデルの設定
ops.model('basic', '-ndm', 2, '-ndf', 3)

# 節点の定義
p0 = [0.0, 0.0]
p1 = [0.0, 2.0]
p2 = [1.0, 2.0]
ops.node(0, *p0)
ops.node(1, *p1)
ops.node(2, *p2)

# 境界条件
const0 = [1, 1, 1]
ops.fix(0, *const0)

# 材料の定義
ops.uniaxialMaterial('Elastic', 0, 3000.0)

# geotransf
ops.geomTransf('Linear', 0) # よくわからん

# 部材の定義
A = 5.0 # 断面積
E = 3000 # ヤング率
Iz = 2 # 断面二次モーメント
ops.element('elasticBeamColumn', 0, *[0, 1], A, E, Iz, 0)
ops.element('elasticBeamColumn', 1, *[1, 2], A, E, Iz, 0)

# 荷重の定義
ops.timeSeries('Constant', 0) # 時間依存性タイプの定義
ops.pattern('Plain', 0, 0) # 荷重タイプの定義
ops.load(2, *[0, -10, 0]) # 荷重の定義

# define and run analysis 

# create SOE
ops.system("BandSPD")

# create DOF number
ops.numberer("Plain")

# create constraint handler
ops.constraints("Plain")

# create integrator
ops.integrator("LoadControl", 1.0)

# create algorithm
ops.algorithm("Linear")

# create analysis object
ops.analysis("Static")

# perform the analysis
ops.analyze(1)


# result of the analysis

N1=ops.basicForce(0)
N2=ops.basicForce(1)
print("N0=",N1,"N1=",N2)

次回は今回の解析結果をもとに曲げモーメント図，軸力図，せん断力図等の基本的な図を描画する方法を説明します．