「pythonで遺伝的アルゴリズム（GA）を実装して巡回セールスマン問題（TSP）をとく」 をやってみた

はじめに

Qiita初投稿のため、内容だけでなく形式や書き方についてなどあらゆる野次をください。

pythonで遺伝的アルゴリズム（GA）を実装して巡回セールスマン問題（TSP）をとく

を実際にやってみました。
コーディングに慣れればいちいち言及しなくて良いのでろうなぁと思いつつ、
気になったことをなるべく記録していきます。

ここをめちゃくちゃ参考(&引用)にしています。

いきなりぼやき

上にも貼ったリンク先のコードをそのままコピペしてもうまく動作しないことがありました。
それは当然で例えば

こんなこと

import numpy as np
import random
import matplotlib.pyplot as plt

を書かなきゃいけない。当然こんな初歩に言及するはずないよなぁ...
スペルミスがあったし...僕もしてるかも...

さぁ本題に入りましょう。

遺伝的アルゴリズム(GA = Genetic Algorithm)とは

優れた遺伝子を持つものの子孫が繁栄する。
遺伝的アルゴリズムでは、これと同じような考え方で優れた解法を繁栄させていく。

子孫繁栄

あらゆる要素について優位な個体がたくさんの子を産み、
劣位の個体はわずかな子しか産めない。
さらに同じことが子世代から孫世代への移動でも起こる。
この繰り返しにより環境に対して適応した洗練された子たちが生まれる。

突然変異

交叉が続いていくと、似たような個体ばかりになる。我々の遺伝子は突然変異を時々起こすことで多様性を担保している。

巡回セールスマン問題(TSP = Travelling Salesman Problem)とは

巡回セールスマン問題は、
セールスマンがn個の営業先をどのような順番でまわるのが良いかと言う類の問題のことで、
理論上n!通りの順路があるため総当たりはしんどいって言うやつ。

今回はこのTSPを用いてGAを解いてみたい。

フロー

引用元

初期個体生成

初期個体として、都市と遺伝子を作る必要があります。

都市

x,y座標がともに0~1の範囲にある都市をn個生み出します。
入力は都市数、出力は(都市数)×２の行列
実装例:generate_rand_cities

#都市を生成
def generate_rand_cities(num_cities):
    positions = np.zeros((num_cities, 2))
    for i in range(num_cities):
        positions[i, 0] = random.random()
        positions[i, 1] = random.random()
    return positions
#試しに
generate_rand_cities(10)

randomについて(random.random)

random.random()

は0.0以上1.0未満の浮動小数点数をランダムに生成

遺伝子

遺伝子に都市を巡る順序についての情報を持たせます。
遺伝子の長さは都市の数と一致させます。
例えば都市の数が6の時は、
[3, 5, 1, 0, 4, 2]
[0, 4, 2, 1, 5, 3]
などのような個体が考えられます。

遺伝子は一世代のうちに複数の個体作るため、
遺伝子は(遺伝子の個体数)×(都市の個数)の行列で表されます。

入力は都市の数と一世代の個体数、出力は(遺伝子の個体数)×(都市の個数)の行列

実装例:generate_init_genes

#遺伝子を生成
def generate_init_genes(num_individual, num_cities):
    genes = np.zeros((num_individual, num_cities), dtype=np.int16)
    for i in range(num_individual):
        genes[i,] = random.sample(range(num_cities), k=num_cities)
    return genes
#試しに
generate_init_genes(15,10)

randomについて(random.sample)

random.sampleは重複なしでランダムに取り出す。
例えば

l = [0, 1, 2, 3, 4]
random.sample(l, 3)

で[4, 2, 1]や[1, 0, 3]といったものが出力される。

評価

今回の課題では、より短い経路を示す遺伝子が高く評価される必要がある。
そのために、まずは遺伝子に対応する経路の長さを求める。
その後、世代内で比較し評価する。

遺伝子に対応する経路

参考元では遺伝子ごとに都市間の距離を計算していた。
都市間の距離についてのテーブルを作り、遺伝子の順序に合わせて参照する。

都市間の距離のテーブル

実装例

#都市間の距離についてのテーブル
def generate_dist_table(positions):
    path_table = np.zeros((len(positions), len(positions)))
    for i in range(len(positions)):
        for j in range(len(positions)):
            path_table[i,j] = np.linalg.norm(positions[i]-positions[j])
    return path_table

#試しに
num_cities = 4
positions = generate_rand_cities(4)
generate_dist_table(positions)

ある2都市の距離について2回計算している。ここはまだ削れるなぁ...

遺伝子に対応する経路の長さ

このテーブルをもとに遺伝子に対応する経路の長さを求める。

#テーブルを参照して、遺伝子に対応させた経路の和を求める
def sum_path2(path_table, gene):
    sum = 0.
    for i in range(len(gene)-1):
        sum += path_table[int(gene[i]),int(gene[i+1])]
    return sum

#試しに
cities = generate_rand_cities(10)
genes = generate_init_genes(15,10)
dist_table = generate_dist_table(cities)
for i in range(len(genes)):
    print(sum_path2(dist_table, genes[i]))

世代ごとに遺伝子の評価をまとめて行いため、一世代の遺伝子についてまとめて出力する関数を設定する。

#経路の和について、一世代計算
def genes_path2(path_table, genes):
    pathlength_vec = np.zeros(len(genes))
    for i in range(len(genes)):
        pathlength_vec[i] = sum_path2(path_table, genes[i])
    return pathlength_vec

#試しに
cities = generate_rand_cities(10)
genes = generate_init_genes(15,10)
dist_table = generate_dist_table(cities)
genes_path2(dist_table, genes)

ルーレット

遺伝子に対応する経路の長さがわかった。今回は経路が短いものほど高く評価したい。
経路が短いものほど子孫を残すものとして選ばれる確率を高くしたい。
正規化を行う。

#ルーレット
def generate_roulette(fitness_vec):
    total = np.sum(fitness_vec)
    roulette = np.zeros(len(fitness_vec))
    for i in range(len(fitness_vec)):
        roulette[i] = fitness_vec[i]/total
    return roulette

#試しに
fitness = np.array([20,50,30])
generate_roulette(fitness)

これに対して

array([0.2, 0.5, 0.3])

となる。

遺伝子をいざ評価

遺伝子に対応する経路の長さはすでにわかった。
今回は経路が短いものほど高く評価したい。
経路が短いものほど子孫を残すものとして選ばれる確率を高くしたい。
そのために今回は経路の長さの逆数を用いる。

#ルーレット実行例
cities = generate_rand_cities(20)
genes = generate_init_genes(21, 20)
dist_table = generate_dist_table(cities)
paths = genes_path2(dist_table, genes)
inverse_path = 1/paths
print("path length: "+str(paths))
print("roulette table: "+str(generate_roulette(inverse_path)))

roulette tableは合計が１となるため、対応する遺伝子が選択される確率と解釈できる。
これを利用して遺伝子の選択を行う。

選択(淘汰)

#ルーレットをもとに交叉をする個体を選ぶ
def roulette_choice(fitness_vec):
    roulette = generate_roulette(fitness_vec)
    choiced = np.random.choice(len(roulette), 2, replace=True, p=roulette)
    return choiced

#試しに
cities = generate_rand_cities(20)
genes = generate_init_genes(21, 20)
dist_table = generate_dist_table(cities)
fitness_vec = 1 / genes_path2(dist_table, genes)
roulette_choice(fitness_vec)

generate_rouletteでルーレットテーブルを作る。
ルーレットテーブルをもとにrouletteの中から２つの遺伝子を選ぶ。

randomについて(random.choice)

random.choiceは重複ありでランダムに値を選ぶ。
第1引数が選ぶ数字の範囲、
第2引数は選ぶ個数、
replaceで重複ありかなしかを指定(Trueで重複あり)
pでそれぞれが選ばれる確率を指定している。

交叉

roulette_choiceを用いて相対的に優秀な二個体を選ぶことができるようになった。
その二個体を掛け合わせる。
交叉法は遺伝子の形によって、また同じ遺伝子の形に対しても複数ある。
例えば順序交叉や循環交叉などがあるらしい→順序問題へのGAの適用
今回は部分的交叉を行なった。
部分的交叉の方法は以下の画像を参考にしていただきたい。引用元

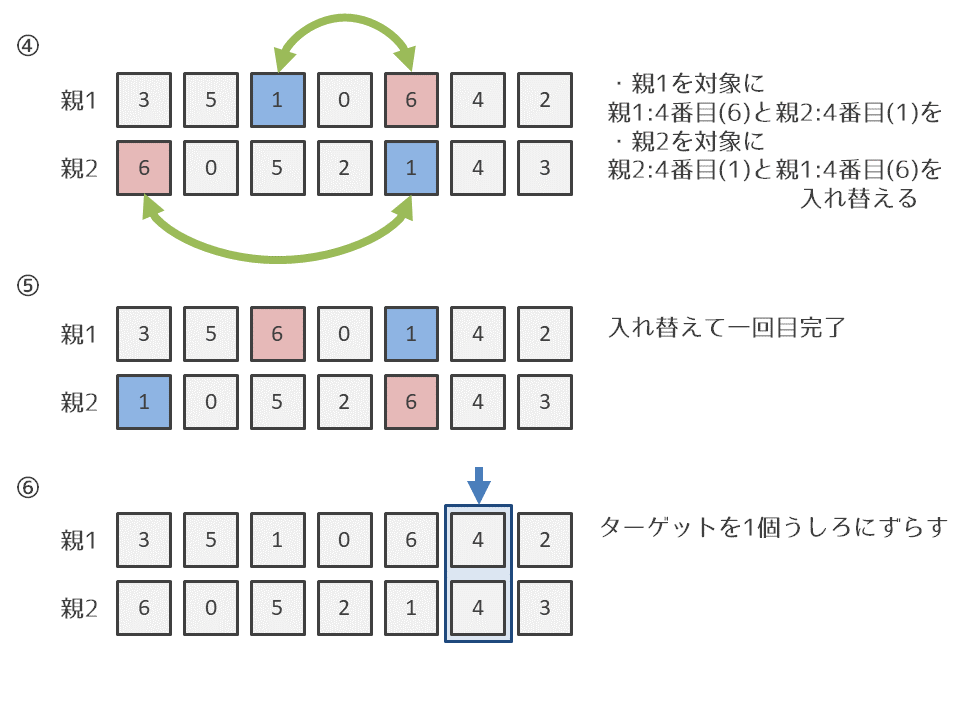
部分的交叉の実装

#部分的交叉の実装
def partial_crossover(parent1, parent2):
    num = len(parent1)
    cross_point = random.randrange(1,num-1)   #切れ目
    child1 = parent1
    child2 = parent2
    for i in range(num - cross_point):
        #切れ目の直ぐ右の値
        target_index = cross_point + i
        target_value1 = parent1[target_index]
        target_value2 = parent2[target_index]
        exchange_index1 = np.where(parent1 == target_value2)
        exchange_index2 = np.where(parent2 == target_value1)
        #交換
        child1[target_index] = target_value2
        child2[target_index] = target_value1
        child1[exchange_index1] = target_value1
        child2[exchange_index2] = target_value2
    return child1, child2

#試しに
genes = generate_init_genes(2, 10)
print("parent1: "+str(genes[0]))
print("parent2: "+str(genes[1]))
child = partial_crossover(genes[0], genes[1])
print("child1:  "+str(child[0]))
print("child2:  "+str(child[1]))

突然変異

突然変異にも様々な手法がある。
今回は転座と呼ばれるものを行う。
ランダムで選んだ二箇所を入れ替える。

def translocation_mutation2(genes, p_value):
    mutated_genes = genes
    for i in range(len(genes)):
        mutation_flg = np.random.choice(2, 1, p = [1-p_value, p_value])
        if mutation_flg == 1:
            mutation_value = np.random.choice(genes[i], 2, replace = False)
            mutation_position1 = np.where(genes[i] == mutation_value[0])
            mutation_position2 = np.where(genes[i] == mutation_value[1])
            mutated_genes[i][mutation_position1] = mutation_value[1]
            mutated_genes[i][mutation_position2] = mutation_value[0]
    return mutated_genes

#試しに
genes = generate_init_genes(5, 10)
print("before")
print(genes)
print("after")
print(translocation_mutation2(genes, 0.7))

mutation_flagは確率p_valueで1になる。
よって、遺伝子が確率p_valueで突然変異を起こす。

可視化

フローチャートには書かれていないが、GAの推移を確認するためにmatplotlibを用いて可視化する。

都市の位置

#都市の位置可視化
def show_cities(cities):
    for i in range(len(cities)):
        plt.scatter(cities[i][0], cities[i][1])

#試しに
cities = generate_rand_cities(10)
show_cities(cities)

経路の可視化

def show_route(cities, gene):
    for i in range(len(gene)-1):
        if i == 0:
            plt.text(cities[int(gene[i])][0], cities[int(gene[i])][1], "start")
        else:
            plt.text(cities[int(gene[i])][0], cities[int(gene[i])][1], str(i))
        plt.plot([cities[int(gene[i])][0], cities[int(gene[i+1])][0]], 
                 [cities[int(gene[i])][1], cities[int(gene[i+1])][1]])
    plt.text(cities[int(gene[i+1])][0], cities[int(gene[i+1])][1], "goal")

#試しに
cities = generate_rand_cities(10)
show_cities(cities)
genes = generate_init_genes(10,10)
show_route(cities,genes[0])

統合

これまで作ってきた関数を利用して、TSPをGAで解くプログラムを実装します。

パラメータ

#パラメータ
num_cities = 10
individuals = 21
generation = 10000
elite = 9
p_mutation = 0.01

初期化

#初期化
cities = generate_rand_cities(num_cities)
genes = generate_init_genes(individuals, num_cities)
dist_table = generate_dist_table(cities)
show_cities(cities)
show_route(cities, genes[0])
plt.show()

こんなのが見れるはず

実行部

親世代のうち優秀なelite個と
親世代間の交叉によって生まれた(individual-elite)個の子が子世代を担う。
子世代の中で突然変異が起きて、最終的な子世代が形成される。

#実行部
top_individual=[]  #各世代の最も優れた適応度のリスト
max_fit = 0  #歴代最高の適応度
fitness_vec = np.reciprocal(genes_path2(dist_table, genes))
for i in range(generation):
    children = np.zeros(np.shape(genes))
    for j in range(int((individuals-elite)/2+1)):
        parents_indices = roulette_choice(fitness_vec)
        children[2*j], children[2*j+1] = partial_crossover(genes[parents_indices[0]], genes[parents_indices[1]])

    for j in range(individuals-elite, individuals):
        children[j] = genes[np.argsort(genes_path2(dist_table, genes))[j-individuals+elite]]

    children = translocation_mutation2(children, p_mutation)
    top_individual.append(max(fitness_vec))
    genes = children
    fitness_vec = np.reciprocal(genes_path2(dist_table, genes))
    if max(fitness_vec) > max_fit:  #過去最高の適応度を記録したら、経路を表示する
        max_fit = max(fitness_vec)
        show_cities(cities)
        show_route(cities, genes[np.argmax(fitness_vec)])
        plt.text(0.05, 0.0, "generation: " + str(i) + "  distance: " +str(sum_path2(dist_table,genes[np.argmax(fitness_vec)])))
        plt.show()

top_individualは各世代の最も優れた適応度を格納したリスト。

最後に表示されたものは

のように経路が短くなるような順序で巡ったものになる。
また、

plt.plot(top_individual)

で世代が変わることによる適応度の推移が確認できる。

numpyについて(メモ)

np.reciprocal()→各要素を逆数にしたやつをくれる
np.argmax()→各要素のうち最大のもののインデックスをくれる
np.argsort()→各要素をソートした時のインデックスの順番

まとめ

初期設定として
都市の数、
遺伝子の個体数、
進化の世代数、
eliteの数、
突然変異の確率、
を与えた。

都市の数を増やすと明らかにもっといい経路があるのに、その経路に進化してくれない。
また、計算に時間がかかる
まだまだ改善の余地があるということだ。
考えられる点として、

交叉の仕方

他の交叉の仕方を知らないため、なんともわからない。より適した交叉法があるかも。
また、突然変異と結びつけたい。

突然変異の確率

親の類似度によって突然変異の確率が変わるようにすれば効率がよくなると考えられる。

ピックアップされるエリートの数

今回は初期設定で決めた。
が、これも突然変異の確率と同様、親の類似度で変えたほうがよくなるかも。
試しに、eliteの数を少なくすると適応度が伸びずに振動する。
交叉によって悪い要素を拾わされるから、序盤で適応度の伸びが起きないと考えられる。

世代数

世代数も初期設定によって与えたが、これも改善の余地がある。
世代の数は計算の負担に直接関わってくる。
適応度の変化率から終了条件を設定すれば世代数の指定が必要なくなるだろう。

遺伝子の個体数

同様に遺伝子の個体数も計算に関わる。
個体数が少ないと進化の世代を増やさなければならなくなる。
与えられた都市の数に対して適した割合で設定すれば入力する必要はなくなるだろう。

展望

最終的に都市について入力するだけで、適した経路を導いてくれそう。
そのために、交叉法、突然変異の確率の与え方、遺伝子の個体数と世代数の適した値などについて調べる必要がありそうです。頑張ります。

randomまとめ

・ランダムに要素を一つ選択: random.choice()
・ランダムに複数の要素を選択（重複なし）: random.sample()
・ランダムに複数の要素を選択（重複あり）: random.choices()
・0~1の浮動小数点数をランダムに生成 : random.random()
pythonでrandomを使うより