前回は巡回セールスマン問題(TSP)を全探索法によって解いた。
全探索方によって確実に最短経路が求められるが、都市の数n個に対して、n!に比例して計算量が増える。
今回は、計算量を抑えつつTSPの解を求めようとしていく。
近似アルゴリズム
全探索をせずに最短だと言い切ることはできないが、少なくとも上位10%くらい短い経路を見つけ出したい。
それを成し遂げる方法として、
- 最近傍探索法(Nearest Neighbor Algorithm):ある都市からもっとも近い都市への経路をとり、それを繰り返す。
- 貪欲法(Greedy Algorithm):各都市間で最短距離となるものを見つけ、それらの情報をからいいものを取り込みつつ経路をつくる。評価、いいもの取り込みを繰り返す。
今回は最近傍探索法(Nearest Neighbor Algorithm)を実践する。
最近傍探索法(Nearest Neighbor Algorithm):nn_tsp
最近傍探索法は
ある都市から経路を始め、その都市から一番近い都市へと経路を進め、
その次の都市からさらに次の、まだ訪れていない都市へと経路を進める。
全探索法のn!通りのすべての経路を生成して考えるのに代わって、最近傍探索では1つの経路を生成する。
経路を見つけるのにO(n^2)の時間がかかる。
以下に示すように実装する。
- "ある都市から経路を始め":任意の都市を最初の都市とする。
- "その都市から一番近い都市":関数'nearest_neighbor'を設定する。
- "経路を進め":都市のリストに
appendする。 - "その次の都市から":その次の都市は
tour[-1]で得られる。 - "まだ訪れていない都市":
unvisitedに訪れていない都市を残しておく。
実装例
def nn_tsp(cities):
"""ある都市から経路を始め、その都市から一番近い都市へと経路を進め、
その次の都市からさらに次の、まだ訪れていない都市へと経路を進める。"""
start = first(cities)
tour = [start]
unvisited = set(cities - {start})
while unvisited:
C = nearest_neighbor(tour[-1], unvisited)
tour.append(C)
unvisited.remove(C)
return tour
def nearest_neighbor(A, cities):
"citiesのうち、Aに一番近いものを見つける。"
return min(cities, key=lambda c: distance(c, A))
メモ
pythonではlambdaは関数を象徴的に表す。
lambda c: distance(c, A)はcからAの距離を計算するcについての関数を意味する。
plot_tsp(alltours_tsp, Cities(10))
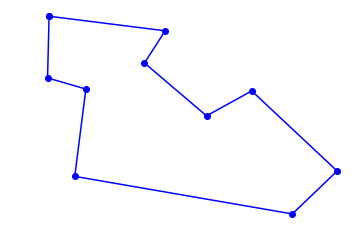
10 city tour with length 2291.8 in 2.302 secs for alltours_tsp
plot_tsp(nn_tsp, Cities(10))
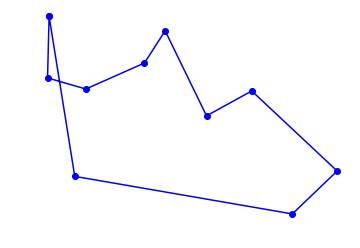
10 city tour with length 2381.4 in 0.000 secs for nn_tsp
実行してみると上記のように、かなり速く計算ができるが、最短のものを見つけていない。
問題点をあぶり出すためにどこを始点としたのかを表示させたい。
plot_tourを修正する。
plot_tour改良(始点を赤くする。)
def plot_tour(tour):
"都市を点、経路を線で示す。始点となった都市を赤い四角で示す。"
start = tour[0]
plot_lines(list(tour) + [start])
plot_lines([start], 'rs') # 始点となった都市を赤い四角で表示。
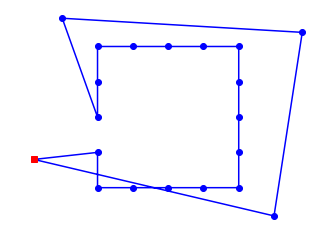
plot_tsp(nn_tsp, Cities(10))
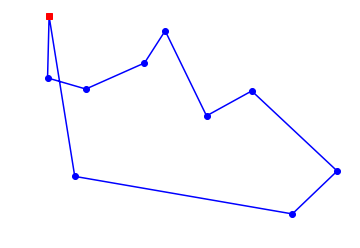
10 city tour with length 2381.4 in 0.000 secs for nn_tsp
始点の都市から、時計回りに経路が作られていったことがわかる。
概ね悪くない経路だが最適ではない。
length_ratio
経路を求めるアルゴリズムのパフォーマンスを比較したい
例えば異なる11セットの都市群とかについてとか
def length_ratio(cities):
"nn_tspによって求まる経路とalltours_tspによって求まる経路の比"
return tour_length(nn_tsp(cities)) / tour_length(alltours_tsp(cities))
sorted(length_ratio(Cities(8, seed=i*i)) for i in range(11))
[1.0, 1.0, 1.0, 1.0, 1.0118279018107388, 1.0121039193389436, 1.107851821362778, 1.139713084817861, 1.1531140497779002, 1.1972133336642432, 1.2160497559961319]
以上からnn_tspは、10セットのうち4つは最適解を見つけられたが、最悪の場合21%も長い経路を求めたことがわかる。
しかし、nn_tspは非常に計算が速くなされ、全探索では計算することが現実的ではない問題に対しても一瞬で答えを示す。
plot_tsp(nn_tsp, Cities(1000))

1000 city tour with length 21275.9 in 0.134 secs for nn_tsp
nn_tspの計算の速さと全探索の最適さを兼ね備えるような改良をしたい。
repeated_nn_tsp
nn_tspでは経路が求まるに連れて終盤の経路は長い直線となっている。
これは、周りに未選択の都市がなくなるからである。
このことから、開始地点を変えればもっといい経路を求められることがありそう。
開始地点を変えて繰り返し試してみよう。
def repeated_nn_tsp(cities):
"各地点を始点としてnn_tspを走らせて、最短となるものを探す。"
return shortest_tour(nn_tsp(cities, start)
for start in cities)
nn_tspを改良する。startを付け足す。
def nn_tsp(cities, start=None):
"""始点となる都市から経路を始め、その都市から一番近い都市へと経路を進め、
その次の都市からさらに次の、まだ訪れていない都市へと経路を進める。"""
if start is None: start = first(cities)
tour = [start]
unvisited = set(cities - {start})
while unvisited:
C = nearest_neighbor(tour[-1], unvisited)
tour.append(C)
unvisited.remove(C)
return tour
# nn_tsp と repeated_nn_tsp を比較
plot_tsp(nn_tsp, Cities(100))
plot_tsp(repeated_nn_tsp, Cities(100))
すると
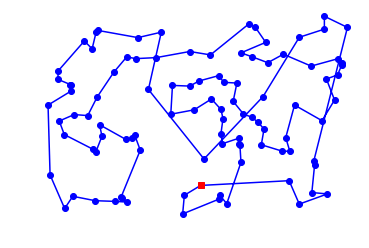
100 city tour with length 6734.1 in 0.003 secs for nn_tsp
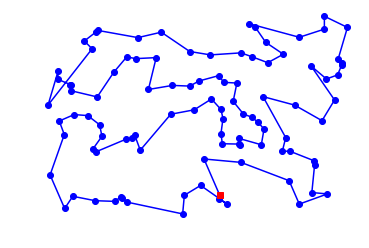
100 city tour with length 5912.6 in 0.135 secs for repeated_nn_tsp
以上のようにかかる時間は増えたが明らかにいい経路を選べるようになった。"繰り返す"ということは強い!
しかし、repeated_nn_tspで最適の経路が求められるわけではない。それなのに都市の数倍時間がかかるようになるのは嬉しくない。そこでありうる全始点からの経路を計算し比較するのではなく、いくつかの都市を始点候補として選び出してより良い経路を求めてみよう。
改良版repeated_nn_tsp(限定的繰り返し)
def repeated_nn_tsp(cities, repetitions=100):
"指定したいくつかの都市をそれぞれ始点としてnn_tspを繰り返す。"
return shortest_tour(nn_tsp(cities, start)
for start in sample(cities, repetitions))
def sample(population, k, seed=42):
"populationから選び出されたk個の要素を持つリストを出力する。random.seedを利用して繰り返し同じ結果を得ることもできるようにした。"
if k is None or k > len(population):
return population
random.seed(len(population) * k * seed)
return random.sample(population, k)
300都市のマップで1,10,100始点で比べてみよう。
def repeat_10_nn_tsp(cities): return repeated_nn_tsp(cities, 10)
def repeat_100_nn_tsp(cities): return repeated_nn_tsp(cities, 100)
plot_tsp(nn_tsp, Cities(300))
plot_tsp(repeat_10_nn_tsp, Cities(300))
plot_tsp(repeat_100_nn_tsp, Cities(300))

299 city tour with length 12752.7 in 0.013 secs for nn_tsp

299 city tour with length 12070.6 in 0.117 secs for repeat_10_nn_tsp
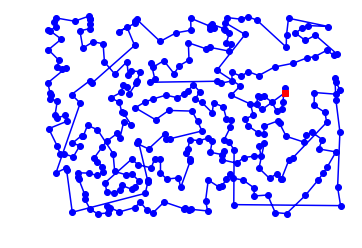
299 city tour with length 11598.6 in 1.126 secs for repeat_100_nn_tsp
経路改善alter_tour
最近傍探索の問題点:外れ値
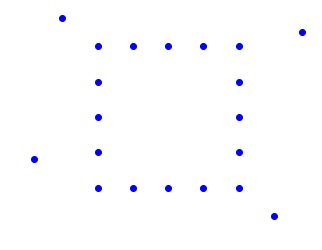
こんな都市を考えてみる
outliers_list = [City(2, 2), City(2, 3), City(2, 4), City(2, 5), City(2, 6),
City(3, 6), City(4, 6), City(5, 6), City(6, 6),
City(6, 5), City(6, 4), City(6, 3), City(6, 2),
City(5, 2), City(4, 2), City(3, 2),
City(1, 6.8), City(7.8, 6.4), City(7, 1.2), City(0.2, 2.8)]
outliers = set(outliers_list)
plot_lines(outliers, 'bo')
plot_tsp(nn_tsp,outliers)
20 city tour with length 38.8 in 0.000 secs for nn_tsp
問題点を見つけやくするために新しい描画関数を導入する。
def plot_labeled_lines(points, *args):
"""各点をプロット、インデックスの数をラベル。
そして、引数によって線を引く点を与える。
1つの引数ではmatplotlibのスタイル、('ro--'みたいに)
あるいは、複数の点のインデックスのリスト([0,1,2]のように)として与えられる。"""
#点を描き、インデックスの数でラベル
plot_lines(points, 'bo')
for (label, p) in enumerate(points):
plt.text(p.x, p.y, ' '+str(label))
#引数によって指示された線を引く
style = 'bo-'
for arg in args:
if isinstance(arg, str):
style = arg
else:
Xs = [points[i].x for i in arg]
Ys = [points[i].y for i in arg]
plt.plot(Xs, Ys, style)
plt.axis('scaled'); plt.axis('off'); plt.show()
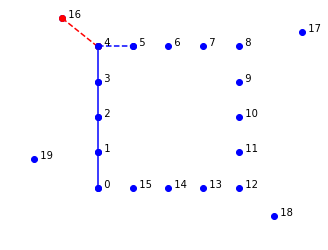
以下の図で最近傍探索をしていると仮定して0番都市から4番都市まで部分的に経路をつくっている。5番都市が最近傍だが、ここで16番都市に行かないと、あとで回収するのに高くつく。
plot_labeled_lines(outliers_list, 'bo-', [0, 11, 2, 9, 4], 'ro--', [4, 16], 'bo--', [4, 5])
時には一番近くの隣に行くより少し遠いところを廻った方が全体として経路が短くなる時がある。いつも一番近くの隣に移動すればいいというわけではない。しかしその塩梅が難しい。そこで代わりとなる手法を考える。一度経路を作ってから、それらを変更することで外れ値やその他の要因による問題を修正していくというものだ。
新単語:セグメント
経路における部分的な都市の連続をセグメントと呼ぶことにする。経路は1つの輪をなすが、セグメントは輪をなさない。
セグメント逆転による経路改変
以下の経路を考えてみる。
cross = [City(9, 3), City(3, 10), City(2, 16), City(3, 21), City(9, 28),
City(26, 3), City(32, 10), City(33, 16), City(32, 21), City(26, 28)]
plot_labeled_lines(cross, range(-1,10))
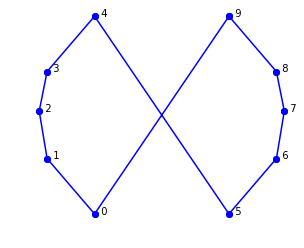
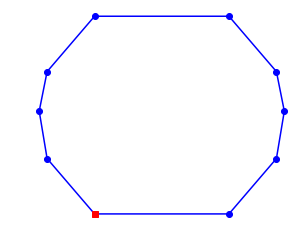
明らかに、良さげな経路じゃない。セグメントを逆転させることで、経路が交差しないようにできる。 経路を[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]と表現する。セグメント[5, 6, 7, 8, 9]を逆転させると経路[0, 1, 2, 3, 4, 9, 8, 7, 6, 5]が得られ、良さげである。確認してみると
tour = Tour(cross)
tour[5:10] = reversed(tour[5:10])
plot_tour(tour)
alter_tour実装
それでは、改善すべきセグメントについて修正してくれる、関数alter_tourを定義していく。
1つのセグメントを変えたら、それによりさらに修正した方がよくなる点が生まれるかもしれない。経路が短くなっていたら、もう一度alter_tourを実行しよう。
def alter_tour(tour):
"セグメントを逆転させることで経路をより短くしようと試す。"
original_length = tour_length(tour)
for (start, end) in all_segments(len(tour)):
reverse_segment_if_better(tour, start, end)
#改善があったならもう一度繰り返し、なければ終了しtourを出力する。
if tour_length(tour) < original_length:
return alter_tour(tour)
return tour
# TO DO: Functions: reverse_segment_if_better, all_segments
セグメントの逆転が改善を生むなら実行する関数を作る。
def reverse_segment_if_better(tour, i, j):
"もし逆転させたセグメント[i:j]によって経路が短くなるなら、逆転させる。"
#元の経路[...A-B...C-D...]に対してB...Cを逆転させた[...A-C...B-D...]を考える。
A, B, C, D = tour[i-1], tour[i], tour[j-1], tour[j % len(tour)]
if distance(A, B) + distance(C, D) > distance(A, C) + distance(B, D):
tour[i:j] = reversed(tour[i:j])
あらゆる始点から取りうるすべての長さのセグメントについて考える。なんとなく長いセグメントから考えた方が早く短くできそう。
def all_segments(N):
"長さNの経路についての全セグメントを表す(始点、終点)の組を出力する。"
return [(start, start + length)
for length in range(N, 2-1, -1)
for start in range(N - length + 1)]
alter_tourがうまくいっているか、
plot_tour(alter_tour(Tour(cross)))
とかで確かめていただきたい。
改変最近傍探索altered_nn_tsp
nn_tspの結果に改変をしたらどうなるか見てみる
def altered_nn_tsp(cities):
return alter_tour(nn_tsp(cities))
試してみよう
plot_tsp(altered_nn_tsp, set(outliers))
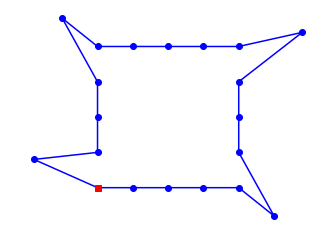
20 city tour with length 26.6 in 0.008 secs for altered_nn_tsp
めっちゃいい感じ。他にもいろいろ試してみて。(Cities(100)とか)
もっとよくできないかな
repeated_altered_nn_tsp
繰り返しと、セグメントによる改変との両方で最近傍探索がよくなった。掛け合わせたらもっとよくなるのでは...?
def repeated_altered_nn_tsp(cities, repetitions=20):
"各nn_tspに対してalter_tourを用いて改善を図る。"
return shortest_tour(alter_tour(nn_tsp(cities, start))
for start in sample(cities, repetitions))
試してみるとどうだろうか。繰り返す分時間がかかるが、より短い経路が見つけられているだろう。
まとめ
最近傍探索法:ある始点からまだ通っていない近いところ、近いところへと経路をつなげていく。nn_tsp
始点が変わると結果が変わるので、いろんな始点の場合を繰り返すことでより良い経路が見つかる。が、繰り返す分時間がかかる。repeated_nn_tsp
→繰り返す回数を調整
近いところに飛びつくから、賢い迂回ができない
→セグメントを逆転させて経路改変altered_nn_tsp
繰り返しとセグメント逆転を掛け合わせてみよう
→repeated_altered_nn_tsp
パラメータ
repeated_nn_tspでも述べたように
- repeatする回数
は求められる精度と時間的制約により調整する必要有
また、今回は全セグメントについて、逆転させると経路が短くなるか調べたが、短いセグメントの改変により全体の経路が大きく改善するとは思えない。よって
- どれくらいのセグメントについて改変を考えるか
もパラメータとして考えられそうである。
以上
次回は非ランダムな地図での実践をしてみます。