Go to Qiita Advent Calendar 2024 Top
LoginSignup
3
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

IBMが提供する製品に関する情報やナレッジを共有するAdvent Calendar 2024

Day 5
@spssfun2017(spss fun)

CPLEXサンプル Staffing（人材割り当て問題、シフト表作成）を読み解く

Last updated at Posted at 2024-12-06

CPLEXのサンプルの Staffing（人材割り当て問題 ）を読み解いていきます。

オリジナルのサンプルは<サンプル導入ディレクトリ>opl/examples/opl/models/Staffing
/staffing.mod
にあります。

  • 実行環境

    • CPLEX 22.1.1
    • Windows 11 64bit

  • サンプル
    □コード

この記事でのサンプルは、オリジナルのサンプルよりデータ量をすくなくし、一部決定変数を集約してわかりやすくしています

□サンプルデータ

問題

飲食店のシフト表を作ります。
各営業日は朝、昼、夜の3つのシフトに分割されており、料理人、会計係の２つの仕事を４人の人員に割り当てます。月曜日から水曜日までのシフトを作ります。

  • 一日のシフトが２シフトである場合、連続である必要があります。朝と夜のシフトのような間を飛ばしたシフトは不可です
  • 一日の間に２シフト以上連続では働けません
  • 夜のシフトで労働する人は、翌日の朝のシフトで労働しません
  • 一人の人が一つのシフト内でできる仕事は料理人、会計係のどちらかのみです
  • 各シフトには、料理人、会計係が最低一人は必要です
  • 人員によってできる仕事が異なります。料理人、会計係両方できる人もいますし、どちらかだけできる人もいます
  • 一部の人員は特定の日に労働できないことがあります

目的は、①各シフトには各仕事の割当要求人数がある。それを満たさないシフト数を最小化する、②作業者のシフトが偏らないようにすることです。

{080A4A6A-22A7-4696-A944-FB6946C43849}.png

利用データ

  1. 人員関連
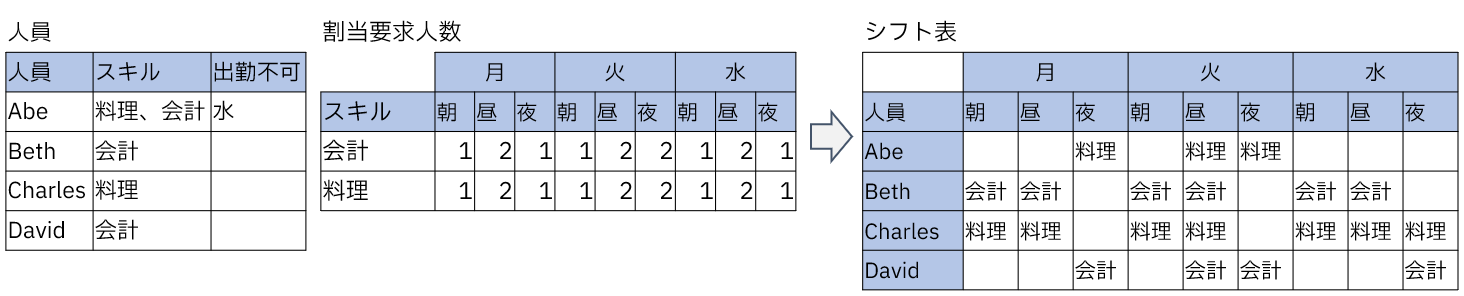
人員 スキル 出勤不可
Abe 料理、会計 水
Beth 会計
Charles 料理
David 会計

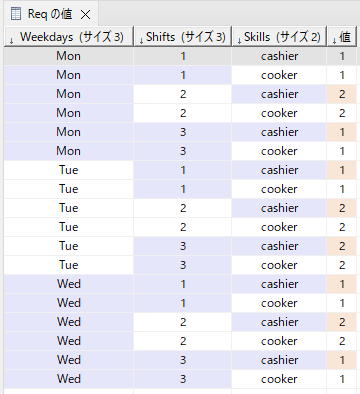
2.割当要求人数

image.png

決定変数

  1. 各曜日、各シフトに人員と割り当てた仕事

目的関数

最小化：以下の①と②の合計
①各シフトには各仕事の割当要求人数がある。それを満たさないシフト数を最小化する。満たさないシフト数＊(総シフト数+1)（ペナルティ）
②作業者のシフトが偏らないようにする。各人員に割り当てられたシフト数の最大差を最小化する

制約

  1. 一日のシフトが２シフトである場合、連続である必要があります。朝と夜のシフトのような間を飛ばしたシフトは不可です
  2. 一日の間に２シフト以上連続では働けません
  3. 夜のシフトで労働する人は、翌日の朝のシフトで労働しません
  4. 一人の人が一つのシフト内でできる仕事は料理人、会計係のどちらかのみです
  5. 各シフトには、料理人、会計係が最低一人は必要です
  6. 人員によってできる仕事が異なります。料理人、会計係両方できる人もいますし、どちらかだけできる人もいます
  7. 一部の人員は特定の日に労働できないことがあります

問題の種類

整数計画

解

実はこの問題は解なしでした。
緩和解として「一日の間に２シフト以上連続では働けません」の制約を緩和して、「水曜日のCharlesが３シフトにでる」という解を返しています。

目的関数

①６(満たさないシフト数)＊7（ペナルティ）
②4(各人員に割り当てられたシフト数の最大差)
=46(ただし緩和解)

決定変数

1.各曜日、各シフトに人員と割り当てた仕事

image.png

2.割当要求人数を満たさないシフト

image.png

OPLコード解説

OPLコードの解説を行っていきます。

利用データ

まず基本データの定義を行っています。

基本データ.mod
int Totalshifts = ...; // １日あたりの総シフト数
int Nbshifts = ...;    // １日あたりに一人が働けるシフト数
range Shifts = 1..Totalshifts; 

{string} Skills = ...;     // スキル
{string} Weekdays = ...;   // 労働曜日 
{string} People = ...;     // 人員

int Req[Weekdays][Shifts][Skills] = ...;  // 各シフトの割当要求人数

定義はstaffing_custom.datファイルの中で行っています。

基本データ.dat
Totalshifts=3;

Nbshifts=2;

// N=2; // 労働者が連続して働けるシフト数

Weekdays={Mon, Tue, Wed};

Skills= {cashier, cooker};

Req = [ 
   [ [1,1], [2,2], [1,1] ],
   [ [1,1], [2,2], [2,2] ], 
   [ [1,1], [2,2], [1,1] ]
   ];

Reqは問題ブラウザで見ると以下のようになっています。
{6B764FB2-391F-4623-B643-D736573C1268}.png

次に人員関連のデータ定義を行っています。

人員の定義
{string} People = ...;     // 人員      
// Data Structure
tuple shift {
  key string p;
  string w;
}

tuple PSkill {
  key string p;
  {string} s;
}

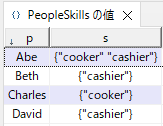
{PSkill} PeopleSkills = ...; //  各人が持つスキルのリスト 
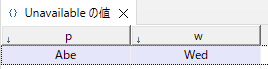
{shift}  Unavailable = ...;  // 各人の出勤不可曜日
人員のデータ
People= {Abe, Beth, Charles, David};

PeopleSkills = { 
 <Abe, {cooker,cashier}>, 
 <Beth, {cashier}>, 
 <Charles,{cooker}>,
 <David,{cashier}>
};

Unavailable = {<Abe, Wed>};

問題ブラウザで見ると以下のようになっています。
{18E06DCB-9A4A-4E59-B474-97AD91FED86B}.png

{3AB2A2C7-15E1-4F2A-8F42-479F5FF7EDF3}.png

次に未割当シフトに対するペナルティの定義を行っています。
出勤可能なシフト数＋１で定義されています。

ペナルティの定義
int Penalty = card(Weekdays)*Nbshifts+1; // 未割当シフトに対するペナルティ

決定変数

次に決定変数の定義を行っています。
dvarが決定変数を意味します。

決定変数１：シフト割り当て

シフトの割当です。

シフト割り当てを示します
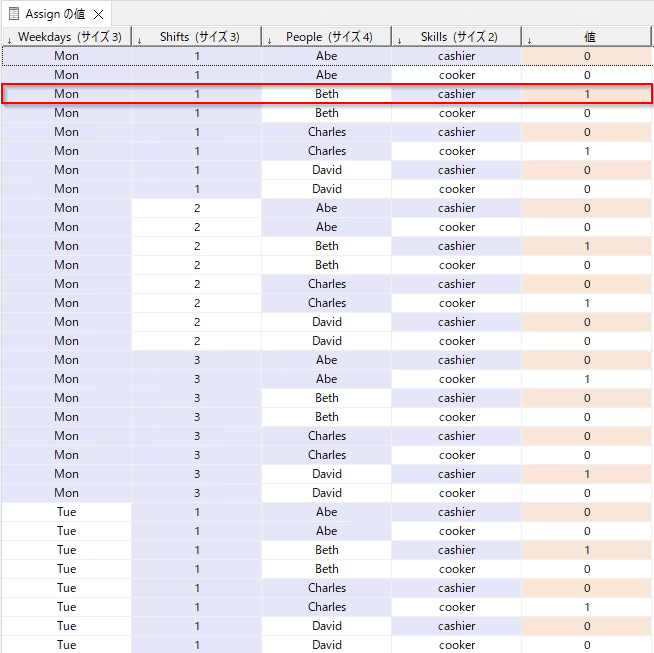
dvar boolean Assign[Weekdays][Shifts][People][Skills];

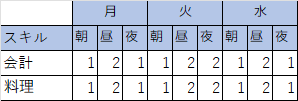
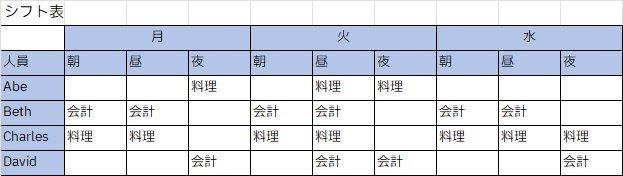
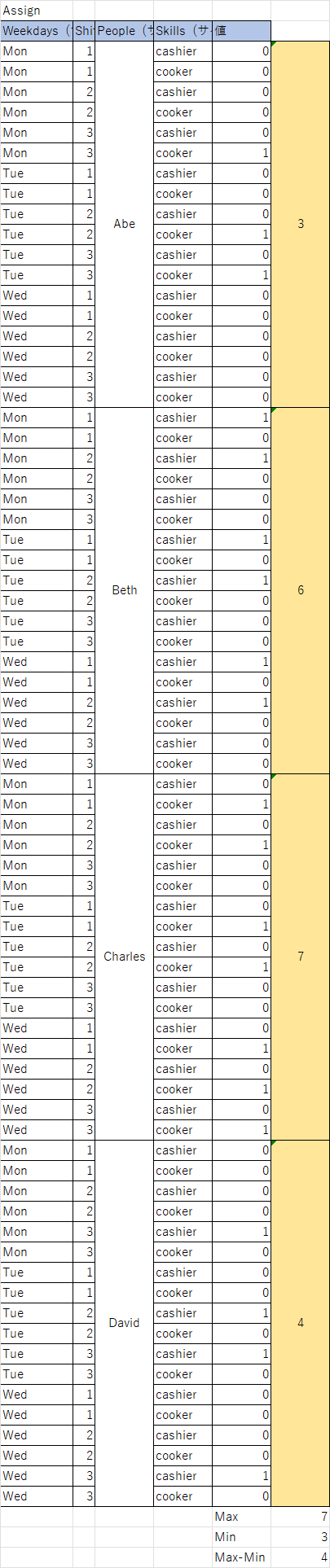
これらの決定変数は、求められた解では以下のようになりました。

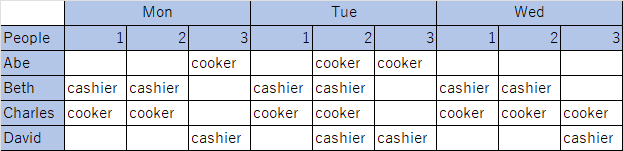
image.png

例えば、Monの朝（１）のBethのシフトはcashierです。
データは縦持ちですが、シフトと人のクロス表で表現すると以下のようになります。
image.png

決定変数２：割当要求人数を満たさないシフト

Reqで定義した割当要求人数を満たさないシフトです。

割当要求人数を満たさないシフト
dvar int Unfilled[Weekdays][Shifts][Skills] in 0..maxint;

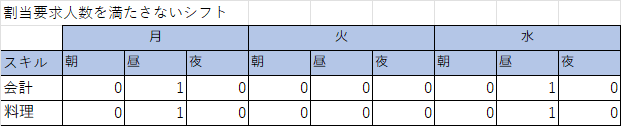
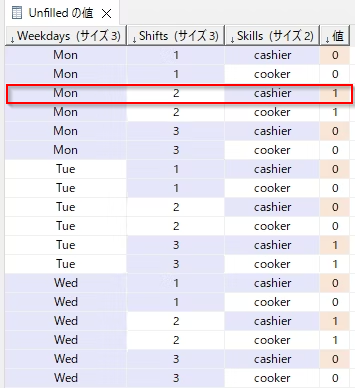
これらの決定変数は、求められた解では以下のようになりました。

image.png

例えば、Monの昼（2）の会計のシフトは割当要求を1名分満たしていません。
やはりデータは縦持ちですが、シフトとスキルのクロス表で表現すると以下のようになります。
image.png

決定変数３：各人各日の勤務の最初のシフト

各人各日の勤務の最初のシフトも定義しています。
これは業務上の問題としては定義されていなかった決定変数ですが、シフトの連続性を制約するために使われています。

各人各日の勤務の最初のシフト
dvar boolean Start[Weekdays][Shifts][People];

これらの決定変数は、求められた解では以下のようになりました。
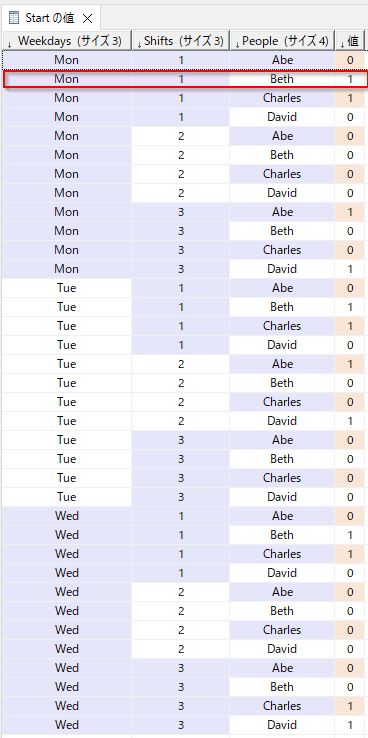
image.png

例えば、BethのMonの最初のシフトは朝（１）です。

目的関数

次に目的関数の定義を行っています。
「①各シフトには各仕事の割当要求人数がある。それを満たさないシフト数を最小化する」ので、まず決定式で割当要求人数を満たさないシフトの総数を計算します。
Unfilledの合計を計算しています。

割当要求人数を満たさないシフトの総数
dexpr int TotUnfilled  =
  sum(w in Weekdays, s in Shifts, j in Skills) Unfilled[w][s][j];

図で表すと以下のようなイメージです。合計で6枠分のシフトが未割当です。
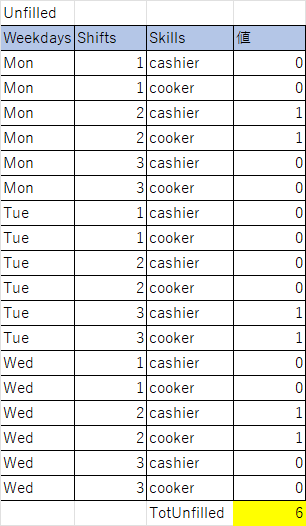
image.png

次に「②作業者のシフトが偏らないようにする。各人員に割り当てられたシフト数の最大差を最小化する」を求めるために、決定式で各人のシフトの総数（PAssign）を計算し、その最大値と最小値の差（Pdiff）を算出します。

各人員に割り当てられたシフト数の最大差
//作業者のシフトが偏らないようにする。各人員に割り当てられたシフト数の最大差
dexpr int PAssign[p in People] = sum(w in Weekdays, s in Shifts, j in Skills) Assign[w][s][p][j];  
dexpr int Pdiff = max(p in People) PAssign[p] - min(p in People) PAssign[p];

image.png

①と②を合わせた値を最小化します。
「①各シフトには各仕事の割当要求人数がある。それを満たさないシフト数を最小化する」を優先するので、Penalty = card(Weekdays)*Nbshifts+1をかけています。「②各人員に割り当てられたシフト数の最大差」は最大でもcard(Weekdays)*Nbshiftsなので、それ以上の数をPenaltyとして①にかけることで①を優先しています。

各人員に割り当てられたシフト数の最大差
minimize TotUnfilled*Penalty + Pdiff;
// Note:  ペナルティは、各人員に割り当てられたシフト数の最大差よりも高いため、スケジュールは常に最初に需要を満たし、次に作業負荷のバランスをとります。

制約

次に制約の定義を行っています。
subject toの中カッコで囲みます。

制約.mod
subject to{

---略----
}

制約1: 一日のシフトが２シフトである場合、連続である必要があります。朝と夜のシフトのような間を飛ばしたシフトは不可です

この制約はCPLEX上のモデル上では三つの制約で実現しています。

制約1-1:シフトが連続すること。シフトk中の人員の数 = kとk-1シフトの開始人員の合計数。

forall(w in Weekdays, s in Shifts) で曜日×シフト分との制約を作っています。
各シフトに割り当てられた人数と、そのシフトとひとつ前のシフトでシフトが始まった人数が同一であることを制約しています。

制約1_1:シフトが連続すること。シフトk中の人員の数 = kとk-1シフトの開始人員の合計数。
  forall(w in Weekdays, s in Shifts)   
      ct01_1:
      sum(p in People, j in Skills) Assign[w][s][p][j] == sum(i in Shifts: s-Nbshifts+1 <= i <= s, j in People) Start[w][i][j];

以下のような制約が定義されました（一部）。
{303AC1C8-04FE-4BAC-B313-66195DEBA810}.png

(i in Shifts: s-Nbshifts+1 <= i <= s)で1シフト前からの合計を求めています。

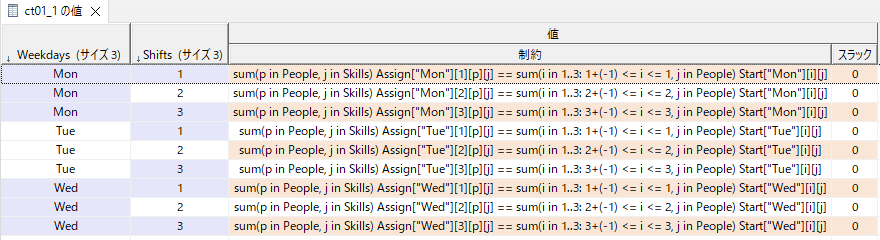
図で表すと以下のようなイメージです（月曜日分のみ）。例えば月曜の昼（２）のシフトはStartの朝（１）、昼（２）の合計とAssignの昼（２）の合計が一致することを示しています。
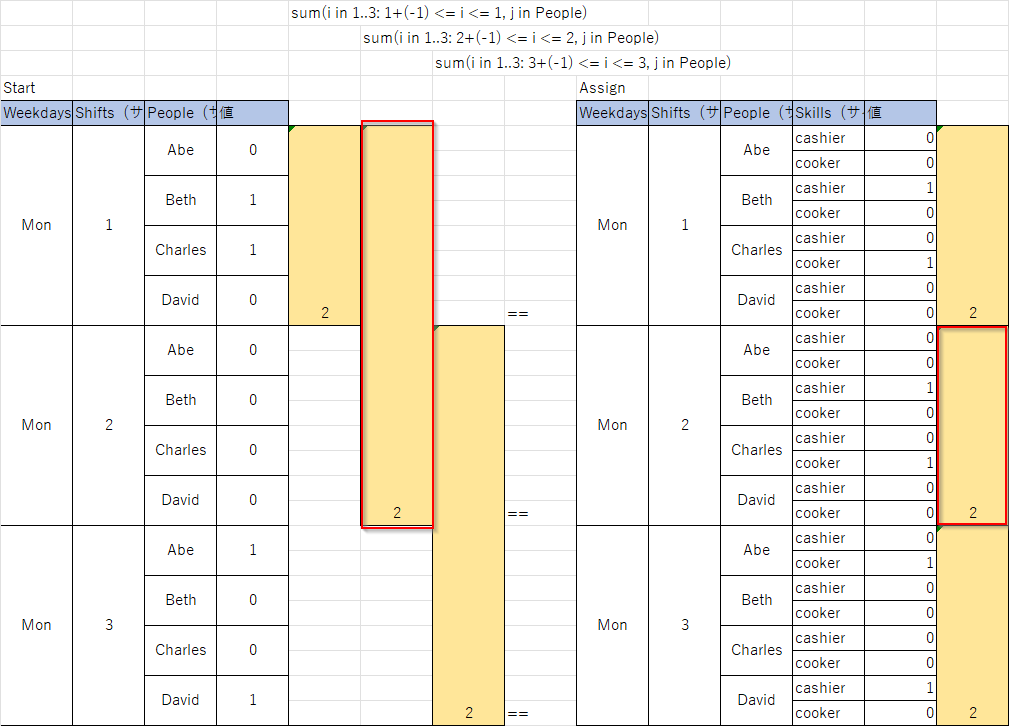
image.png

制約1-2:ある人がシフト k で開始した場合、その人は次の nbshifts シフトで勤務可能になります。

forall(w in Weekdays, s in Shifts,p in People) で曜日×シフト×人分、そしてforall(k in Shifts: s-Nbshifts+1 <= k <= s) で一つ前のシフト分の制約を作っています。
各シフトに割り当てられた人は、そのシフトかひとつ前のシフトでシフトが始まっていることを制約しています。シフトが始まっていないのに割り当てがあることのないように制約されています。

制約1_2:ある人がシフト k で開始した場合、その人は次の nbshifts シフトで勤務可能
  forall(w in Weekdays, s in Shifts,p in People) {
    // ある人がシフト k で開始した場合、その人は次の nbshifts シフトで勤務可能になります。 
    forall(k in Shifts: s-Nbshifts+1 <= k <= s) 
      ct01_2:
      sum(j in Skills) Assign[w][s][p][j] >= Start[w][k][p];

以下のような制約が定義されました（一部）。
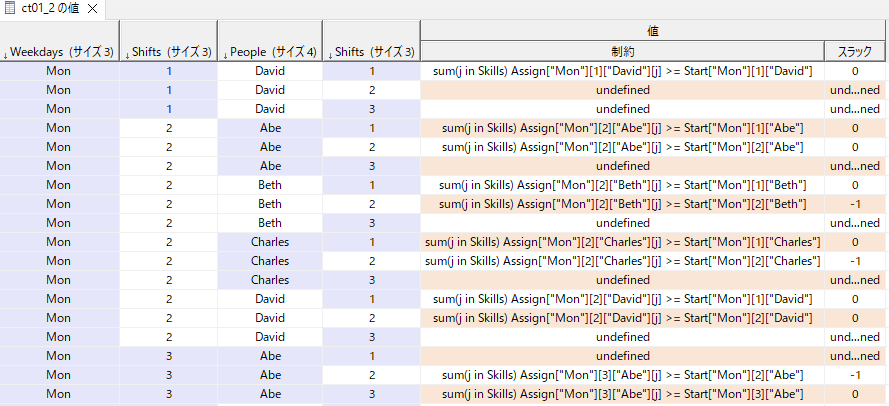
{596FB521-8462-4C71-9B17-54290B5F5CDA}.png

図で表すと以下のようなイメージです（一部のみを表示しています）。例えば月曜の昼（２）のBethのシフトはStartの朝（１）、昼（２）のいずれかで始まっていることを示しています。
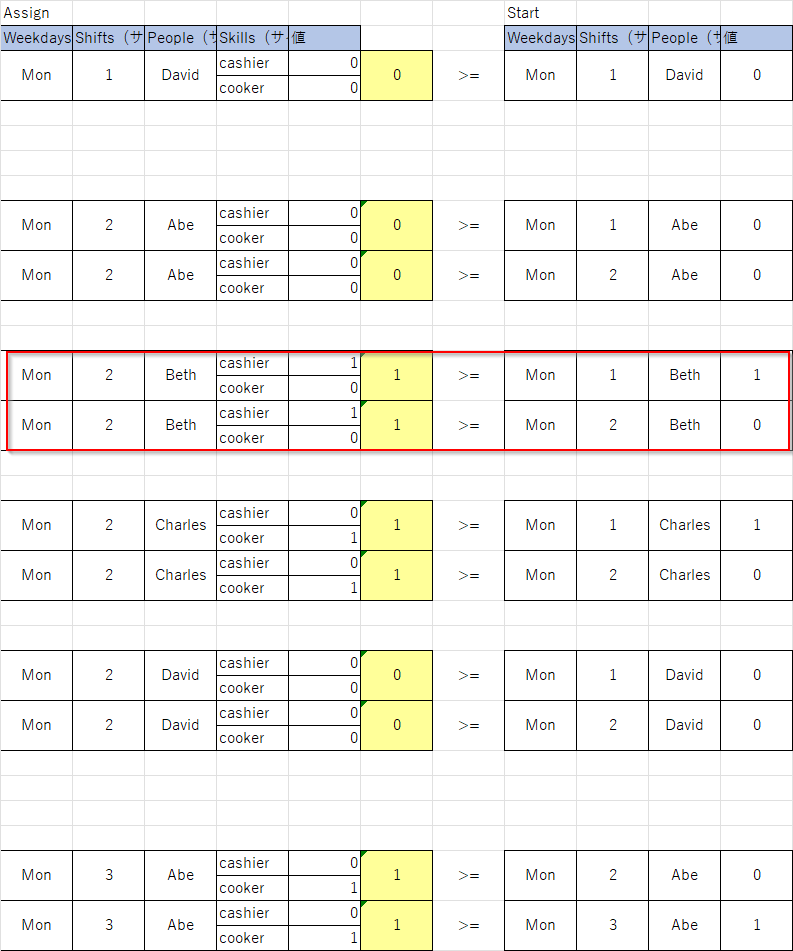
image.png

制約1-3:開始は連続できない。人がすでに開始している場合は、次の nbshifts シフトのいずれでも再度「開始」することはできません

forall(w in Weekdays, s in Shifts,p in People) で曜日×シフト×人分、そしてforall(k in Shifts: s+1 <= k <= s+Nbshifts-1)で一つ後のシフト分の制約を作っています。
一つ前のStartで開始したら、次のStartでは開始ができないことを制約しています。

制約1_3:ある人がシフト k で開始した場合、その人は次の nbshifts シフトで勤務可能
  forall(w in Weekdays, s in Shifts,p in People) {
    // 開始は連続できない。人がすでに開始している場合は、次の nbshifts シフトのいずれでも再度「開始」することはできません。 
    forall(k in Shifts: s+1 <= k <= s+Nbshifts-1) 
      ct01_3:
      1-Start[w][s][p] >= Start[w][k][p];

以下のような制約が定義されました（月曜朝分のみ）。
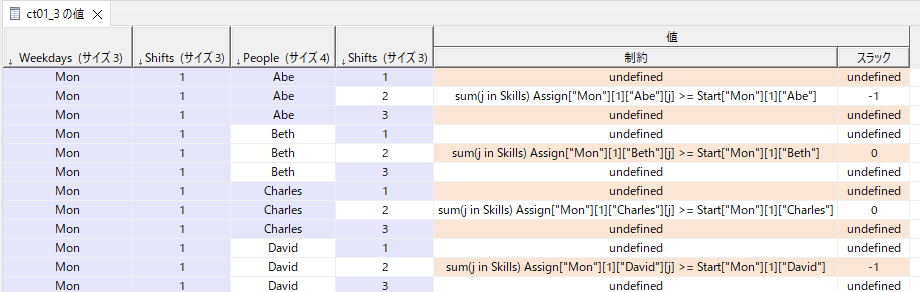
{574897F6-A98A-4FAA-AF86-A0E459635F0E}.png

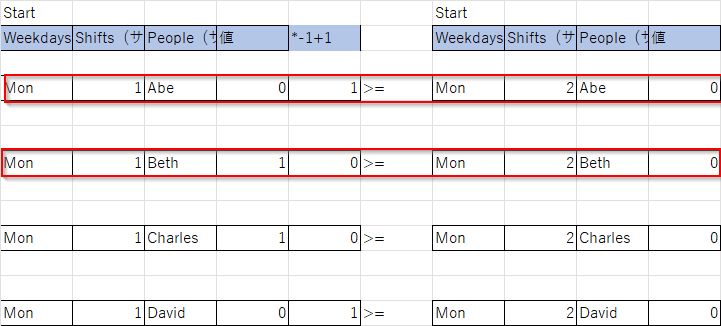
図で表すと以下のようなイメージです（一部のみを表示しています）。
ポイントは直前の開始に*(-1)+1でビットを反転していることです。
例えば月曜の朝（1）のAbeの開始はなかったので、昼（２）の開始はあってもなくてもかまいません。月曜の朝（1）のBethの開始はあったので、昼（２）の開始はあってはいけません（もしあると0>=1になってしまいます）。
image.png

なお、制約の以下の式は

1-Start[w][s][p] >= Start[w][k][p];

以下のように移項して書き換えた方が理解しやすいかもしれません。連続するシフトのStartの合計が１以下になるようにという意味になります。

Start[w][s][p] + Start[w][k][p] <=1;

制約２．一日の間に２シフト以上連続では働けません

forall(w in Weekdays, p in People)で曜日×人分の制約を作っています。

各曜日の1日分のシフト数が２以下を示しています。

制約2:一日の間に２シフト以上連続では働けません
  forall(w in Weekdays, p in People) 
    ct02Shifts:      
      sum(s in Shifts, j in Skills) 
        Assign[w][s][p][j] <= Nbshifts;

以下のような制約が定義されました（月曜分のみ）。
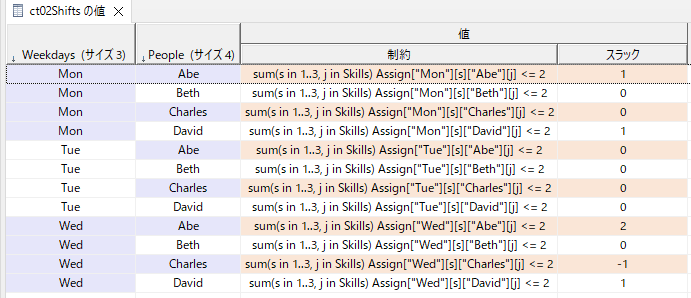
{2CCA4ECF-87E4-4FD7-82AB-E5C9FF057D5A}.png

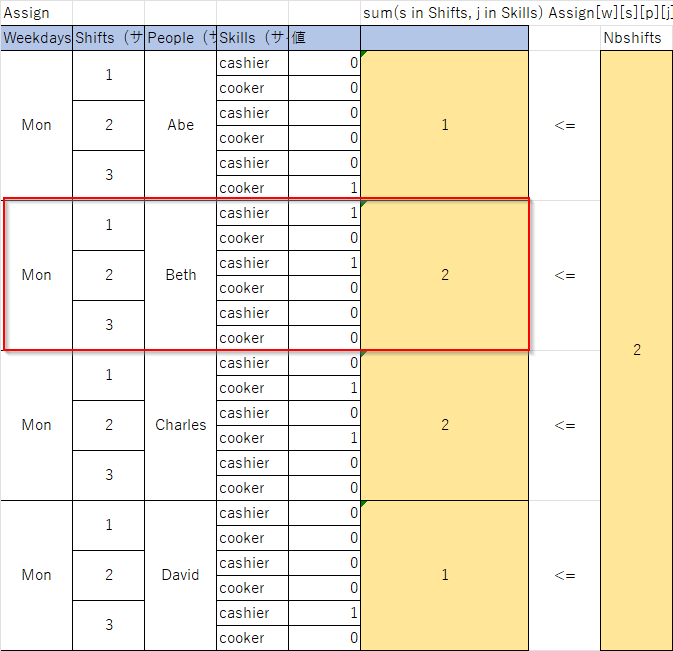
図で表すと以下のようなイメージです（月曜分のみ）。
MonのBethは朝と昼のシフトで2シフトになっています。
image.png

制約３:夜のシフトで労働する人は、翌日の朝のシフトで労働しません

forall(p in People, k in Skills)で人員×スキル分の制約を作っています。

前日の夜（３）シフトがある場合は各人の朝（１）シフトがないようにしています。

Totalshiftsは３なのでここでは夜（３）になっています。
*(-1)+1で夜のシフトをビット反転させています。これによって夜シフトがあった場合は０になり、朝シフトがあると<=が成り立たなくなり制約違反になります。夜シフトがなかった場合は１になるので、朝シフトがあっても<=が成り立ちます。

制約３:夜のシフトで労働する人は、翌日の朝のシフトで労働しません。
  forall(p in People, k in Skills) {
    ct03_1:   
    Assign["Tue"][1][p][k] <= 1 - sum(j in Skills) Assign["Mon"][Totalshifts][p][j];
    ct03_2:   
    Assign["Wed"][1][p][k] <= 1 - sum(j in Skills) Assign["Tue"][Totalshifts][p][j];
  }

以下のような制約が定義されました（火―月分のみ）。
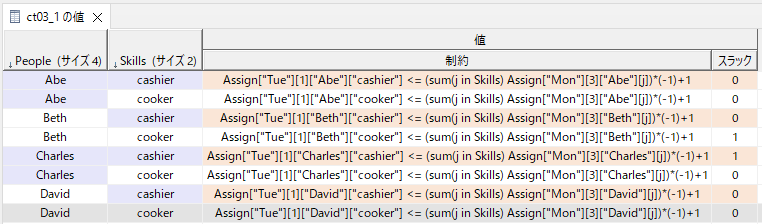
{C102E89F-D6A4-4A0E-BAD4-EA46A524FAFE}.png

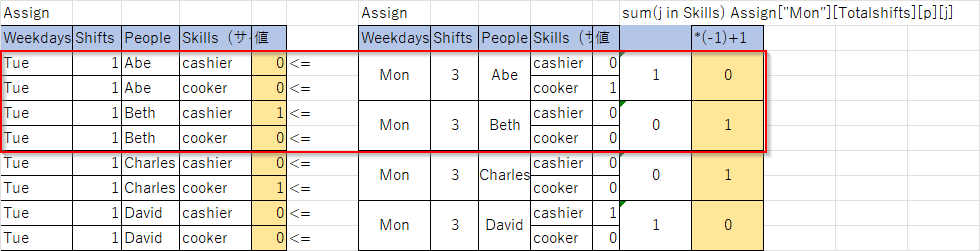
図で表すと以下のようになります火―月分のみ）。
Abeは月曜夜（３）のシフトがあるので火曜朝（１）は0でないといけません。
Bethは月曜夜（３）のシフトがないので火曜朝（１）は1でも構いません。
image.png

制約４:一人の人が一つのシフト内でできる仕事は料理人、会計係のどちらかのみです

forall(w in Weekdays, s in Shifts, p in People)で曜日×シフト×人員分の制約を作っています。

スキルについて合計値をだしてそれが1以下という制約になっています。つまり料理人、会計係のどちらかが1になったら、もう一つのスキルは担当できないということになります。

制約４:一人の人が一つのシフト内でできる仕事は料理人、会計係のどちらかのみです
  forall(w in Weekdays, s in Shifts, p in People) 
    ct04Tasks:      
      sum(j in Skills) 
        Assign[w][s][p][j] <= 1;

以下のような制約が定義されました（一部のみ）。
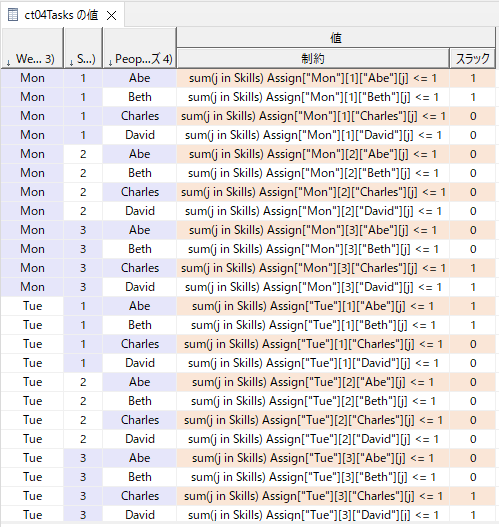
{398CDAC0-501E-4FCA-9D77-770F7AC7FB4D}.png

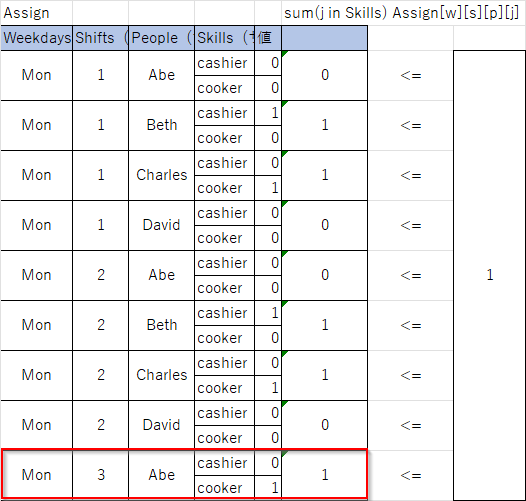
図で表すと以下のようになります（月分のみ）。
Abeは料理人、会計係のどちらも担当可能ですが、月曜夜（３）のシフトでは、料理人のみを担当しています。
image.png

制約５:各シフトには、料理人、会計係が最低一人は必要です

forall(w in Weekdays, s in Shifts, j in Skills)で曜日×シフト×スキル分の制約を作っています。

各シフトの割当要求人数のReqにかかわらず、全てのシフトで料理人と会計係に一人はAssignがあるようにします。

制約５:各シフトには、料理人、会計係が最低一人は必要です
  forall(w in Weekdays, s in Shifts, j in Skills) 
    ct05Skills:
      sum(p in People) Assign[w][s][p][j] >= 1;

以下のような制約が定義されました。
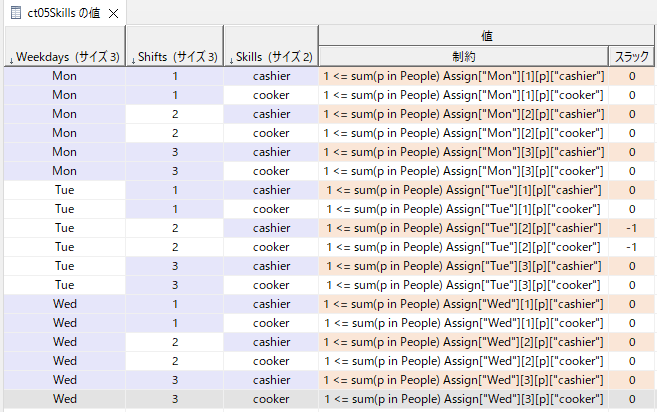
{94418F28-9B0C-47FF-AB85-3D358A0B7933}.png

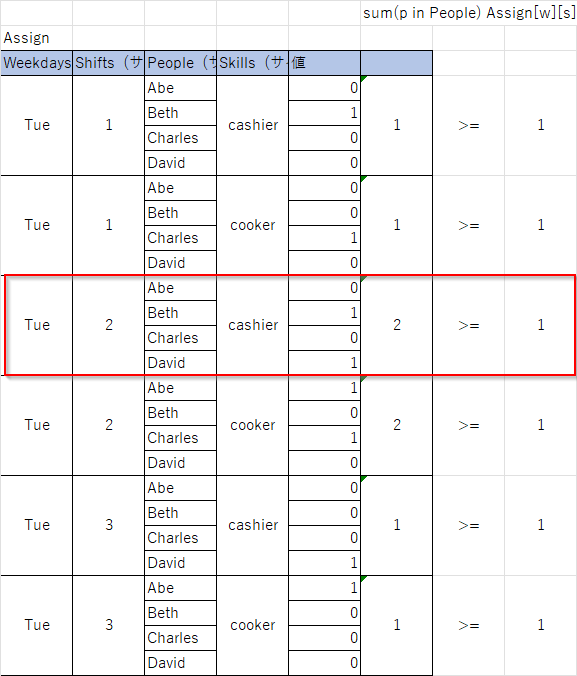
図で表すと以下のようになります(火のみ）。
火曜昼（２）の会計はBethとDavidが割り当てられているので、一人以上が割り当てられています。
image.png

制約６:人員によってできる仕事が異なります。料理人、会計係両方できる人もいますし、どちらかだけできる人もいます

forall(w in Weekdays, s in Shifts, t in PeopleSkills, k in Skills: k not in t.s)で曜日×シフト×PeopleSkillsで定義された人員×not inで持っていないスキル分の制約を作っています。

持っていないスキルのAssignが0であるという制約です。
t.pとt.sは以下のPeopleSkillsから取得しています。
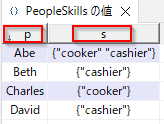
image.png

制約６:人員によってできる仕事が異なります。料理人、会計係両方できる人もいますし、どちらかだけできる人もいます
  forall(w in Weekdays, s in Shifts, t in PeopleSkills, k in Skills: k not in t.s)
    ct06:
    Assign[w][s][t.p][k] == 0;

以下のような制約が定義されました（月のみ）。
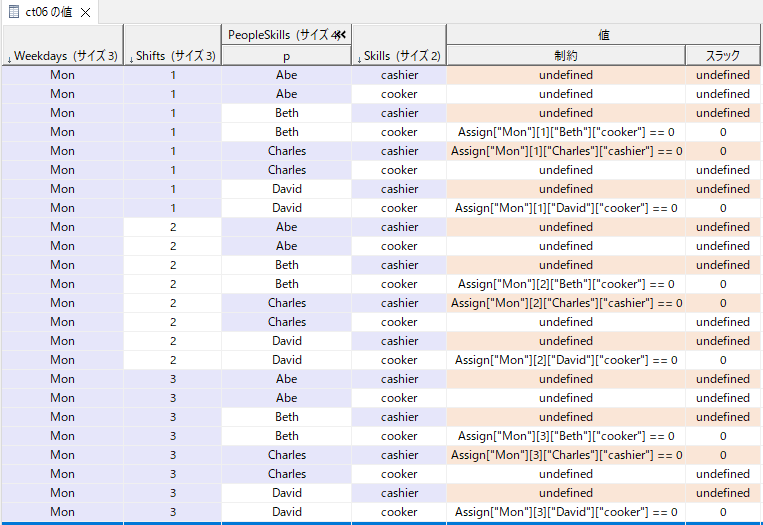
{859B1D49-A865-452C-B921-83C65A28BF74}.png

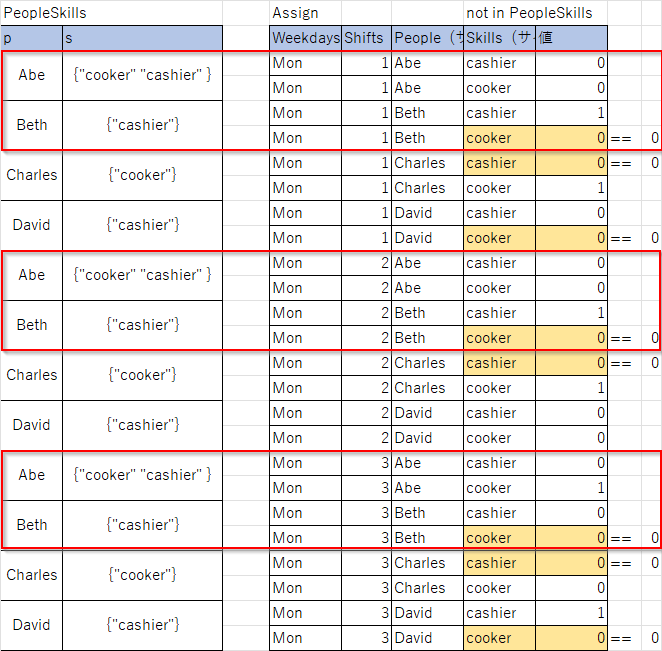
図で表すと以下のようになります(月のみ）。
Abeは料理と会計のスキルを両方持っているので制約はありません。
Bethは会計のスキルは持っていますが、料理のスキルがないので==0の制約があります。
この制約は全てのシフトに対して繰り返して適用されます。
image.png

制約７:一部の人員は特定の日に労働できないことがあります

forall(<p,w> in Unavailable, s in Shifts, j in Skills)で、Unavailableで定義された曜日×人員×シフト×スキル分の制約を作っています。

Unavailableで定義された曜日、人員のAssignが0であるという制約です。
pとwは以下のUnavailableから取得しています。つまりAbeは水曜に出勤できません。
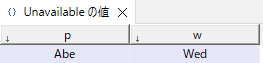
{71F939AB-AAC1-466C-B7A6-2B0E8FC390BC}.png

制約７:一部の人員は特定の曜日に労働できないことがあります
  forall(<p,w> in Unavailable, s in Shifts, j in Skills)
    ct07:
    Assign[w][s][p][j] == 0;

以下のような制約が定義されました。
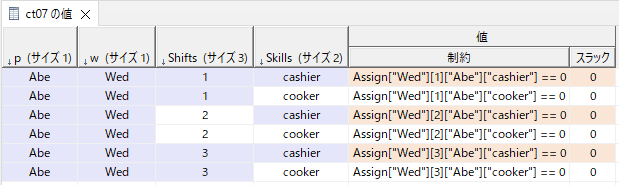
{5C9EA13B-EB3A-42F1-AA7A-58A31CA2B502}.png

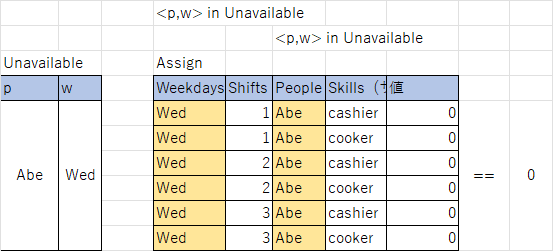
図で表すと以下のようになります。
Abeの水曜のすべてのシフトに==0の制約があります。
image.png

制約８:各シフトにおいて、あるタイプのタスクに割り当てられた人数 + 空いているスロット >= そのタイプの必要な人数 （必要な人数を満たしてなくてもよい ）

この制約は問題の定義にはありませんでした。未割当の人数の決定変数であるUnfilledに値をいれるための制約です。

forall(w in Weekdays, s in Shifts, j in Skills)で、曜日×シフト×スキル分の制約を作っています。

各シフトにアサインされた人数+未割当の人数＞＝割当要求人数なので、割り当て人数に満たない場合にUnfilledへ値が入ります。さらにUnfilledは目的関数でMinimizeされているので、基本的には割当要求人数-各シフトにアサインされた人数=未割当の人数が入ることになります。
ただし、Unfilledは非負で、＞＝の制約なので、割当要求人数よりもアサイン人数を多くすることもこの制約は許容しています。あまりシフトに入っていない人がいる場合には、シフトの平準化の目的関数のために割当要求人数よりも多くの人員をアサインをする可能性があります。

制約８:各シフトにおいて、あるタイプのタスクに割り当てられた人数 + 空いているスロット >= そのタイプの必要な人数 （必要な人数を満たしてなくてもよい ）
  forall(w in Weekdays, s in Shifts, j in Skills)
    ct08Unfilled:    
      sum(p in People) 
        Assign[w][s][p][j] + Unfilled[w][s][j] >= Req[w][s][j];

以下のような制約が定義されました。
{5C9EA13B-EB3A-42F1-AA7A-58A31CA2B502}.png

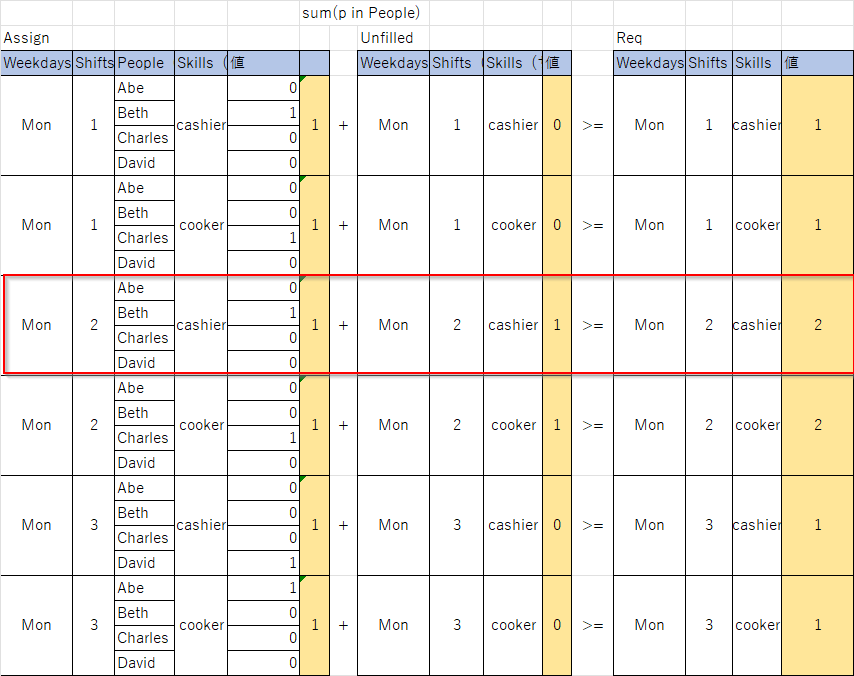
図で表すと以下のようになります。
月曜昼（２）の会計はReqでは2人ですが、Beth1人しか割り当てられていないのでUnfilledが1人になっています。
image.png

完成OPL

製品サンプルとほぼ同じ内容ですが、日本語コメントを入れたり順序を入れ替えたり、添え字を入れ替えたりして読みやすくしています。またオリジナルのサンプルには、PersonnelやAvailという決定変数がありましたが、結局はAssignで表現できていそうだったので、割愛しています。

staffing_customNonAvail2.mod
//**************************** Data **************************************
int Totalshifts = ...; // １日あたりの総シフト数
int Nbshifts = ...;    // １日あたりに一人が働けるシフト数
range Shifts = 1..Totalshifts; 

{string} Skills = ...;     // スキル
{string} Weekdays = ...;   // 労働曜日 


int Req[Weekdays][Shifts][Skills] = ...;  // 各シフトの割当要求人数
          
{string} People = ...;     // 人員       
// Data Structure
tuple shift {
  key string p;
  string w;
}

tuple PSkill {
  key string p;
  {string} s;
}

{PSkill} PeopleSkills = ...; //  各人が持つスキルのリスト 
{shift}  Unavailable = ...;  // 各人の出勤不可曜日

int Penalty = card(Weekdays)*Nbshifts+1; // 未割当シフトに対するペナルティ

//********************************* 決定変数 **********************************
        
dvar boolean Assign[Weekdays][Shifts][People][Skills];   // シフト割り当てを示します
dvar int Unfilled[Weekdays][Shifts][Skills] in 0..maxint;  // 割当要求人数を満たさないシフト
dvar boolean Start[Weekdays][Shifts][People];             // 各人各日の勤務の最初のシフト



/************************************* Model *********************************/
// the total # of slots unfilled in a week
// 割当要求人数を満たさないシフトの総数
dexpr int TotUnfilled  =
  sum(w in Weekdays, s in Shifts, j in Skills) Unfilled[w][s][j];

//作業者のシフトが偏らないようにする。各人員に割り当てられたシフト数の最大差
dexpr int PAssign[p in People] = sum(w in Weekdays, s in Shifts, j in Skills) Assign[w][s][p][j];  
dexpr int Pdiff = max(p in People) PAssign[p] - min(p in People) PAssign[p];

minimize TotUnfilled*Penalty + Pdiff;
// Note:  ペナルティは、各人員に割り当てられたシフト数の最大差よりも高いため、スケジュールは常に最初に需要を満たし、次に作業負荷のバランスをとります。

subject to {
   
  // 制約１: 一日のシフトが２シフトである場合、連続である必要があります。朝と夜のシフトのような間を飛ばしたシフトは不可です
  // シフトが連続すること。シフトk中の人員の数 = kとk-1シフトの開始人員の合計数。
  forall(w in Weekdays, s in Shifts)   
      ct01_1:
      sum(p in People, j in Skills) Assign[w][s][p][j] == sum(i in Shifts: s-Nbshifts+1 <= i <= s, j in People) Start[w][i][j];
               
  forall(w in Weekdays, s in Shifts,p in People) {
    // ある人がシフト k で開始した場合、その人は次の nbshifts シフトで勤務可能になります。 
    forall(k in Shifts: s-Nbshifts+1 <= k <= s) 
      ct01_2:
      sum(j in Skills) Assign[w][s][p][j] >= Start[w][k][p];
    // 開始は連続できない。人がすでに開始している場合は、次の nbshifts シフトのいずれでも再度「開始」することはできません。 
    forall(k in Shifts: s+1 <= k <= s+Nbshifts-1) 
      ct01_3:
      1-Start[w][s][p] >= Start[w][k][p];
  }
   
    
    
  // In each shift,  # of people assigned to a type of task +
  //   unfilled slot >= # of people of that type required
  // 制約８:各シフトにおいて、あるタイプのタスクに割り当てられた人数 + 空いているスロット >= そのタイプの必要な人数 （必要な人数を満たしてなくてもよい ）
  forall(w in Weekdays, s in Shifts, j in Skills)
    ct08Unfilled:    
      sum(p in People) 
        Assign[w][s][p][j] + Unfilled[w][s][j] >= Req[w][s][j];

  // 制約６:人員によってできる仕事が異なります。料理人、会計係両方できる人もいますし、どちらかだけできる人もいます  
  forall(w in Weekdays, s in Shifts, t in PeopleSkills, k in Skills: k not in t.s)
    ct06:
    Assign[w][s][t.p][k] == 0;
        
  // 制約２:一日の間に２シフト以上連続では働けません
  forall(w in Weekdays, p in People) 
    ct02Shifts:      
      sum(s in Shifts, j in Skills) 
        Assign[w][s][p][j] <= Nbshifts;
        
  // 制約７:一部の人員は特定の曜日に労働できないことがあります
  forall(<p,w> in Unavailable, s in Shifts, j in Skills)
    ct07:
    Assign[w][s][p][j] == 0;
  
  // Each person can take only one task in each shift     
  // 制約４:一人の人が一つのシフト内でできる仕事は料理人、会計係のどちらかのみです     
  forall(w in Weekdays, s in Shifts, p in People) 
    ct04Tasks:      
      sum(j in Skills) 
        Assign[w][s][p][j] <= 1;
 
  // If a person is on a night shift, he cannot be assigned to the morning
  //  shift the next day
  // 制約３:夜のシフトで労働する人は、翌日の朝のシフトで労働しません
  forall(p in People, k in Skills) {
    ct03_1:   
    Assign["Tue"][1][p][k]+ sum(j in Skills) Assign["Mon"][Totalshifts][p][j] <= 1 ;
    // Assign["Tue"][1][p][k] <= 1 - sum(j in Skills) Assign["Mon"][Totalshifts][p][j];
    ct03_2:   
    Assign["Wed"][1][p][k] <= 1 - sum(j in Skills) Assign["Tue"][Totalshifts][p][j];
  }
  
  //Each shift has at least a cook, a cleaner and a cashier
  //制約５:各シフトには、料理人、会計係が最低一人は必要です
  forall(w in Weekdays, s in Shifts, j in Skills) 
    ct05Skills:
      sum(p in People) Assign[w][s][p][j] >= 1;     
}

データはわかりやすくするためにスタッフ数やシフト数をオリジナルのサンプルよりも減らして小さくしています。

stuffing.custom.dat
// １日あたりの総シフト数
Totalshifts=3;
// １日あたりに一人が働けるシフト数
Nbshifts=2;

// N=2; // 労働者が連続して働けるシフト数
// 労働曜日
Weekdays={Mon, Tue, Wed};
// スキル
Skills= {cashier, cooker};


// 各シフトに必要なスキルタイプの人数
Req = [ 
   [ [1,1], [2,2], [1,1] ],
   [ [1,1], [2,2], [2,2] ], 
   [ [1,1], [2,2], [1,1] ]
   ];

//Shifts= { 8to12, 12to4, 4to8};
// 人員 
People= {Abe, Beth, Charles, David};
// 各人が持つスキルのリスト
PeopleSkills = { 
 <Abe, {cooker,cashier}>, 
 <Beth, {cashier}>, 
 <Charles,{cooker}>,
 <David,{cashier}>
};
// 各人の出勤不可曜日
Unavailable = {<Abe, Wed>};
//Unavailable = {};

実行

緩和解

実はこの問題は実行可能解がありません（もともとのサンプルは実行可能ですが、簡単にするためにStaffの数などを減らしたため実行可能解がなくなっています）。そのため出てきた結果は、制約が一部緩和された緩和解になっています。

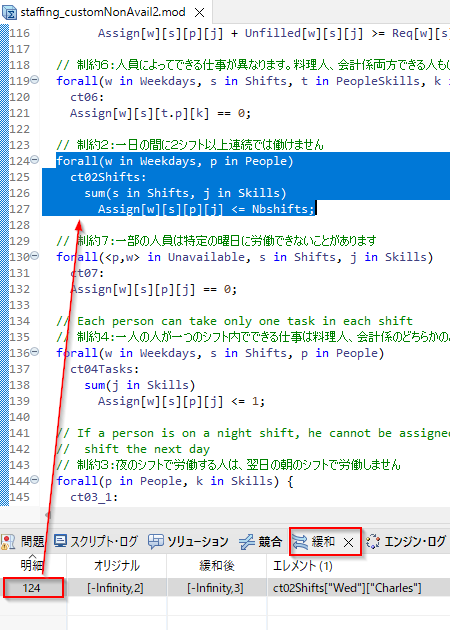
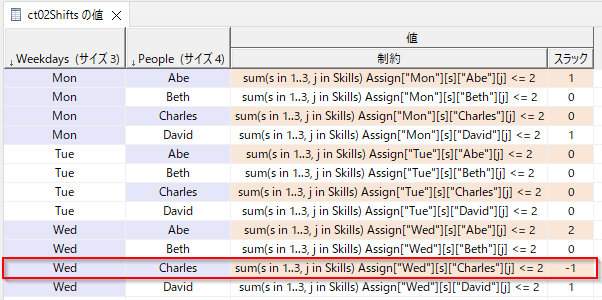
緩和タブを開くと制約２に抵触していて、水曜日のCharlesが2シフト以上アサインした緩和解になっていることがわかります。クリックすると対象となっている制約のOPLコードが開きます。

image.png

制約２を見てみるとスラックが-1になっていて制約違反をしていることがわかります。
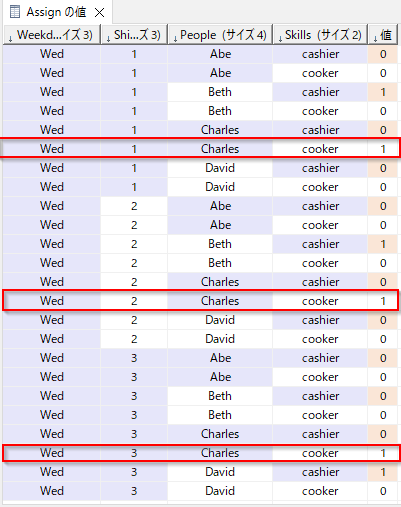
image.png

Assignを確認すると確かにCharlesは朝昼夜の3シフトにアサインされています。
image.png

競合の解決

CPLEXが出してきた緩和解を受け入れられない場合は、別の制約を緩めるか、データを修正していきます。
競合タブを開くと競合した制約が表示されます。クリックすると対象となっている制約のOPLコードが開きます。

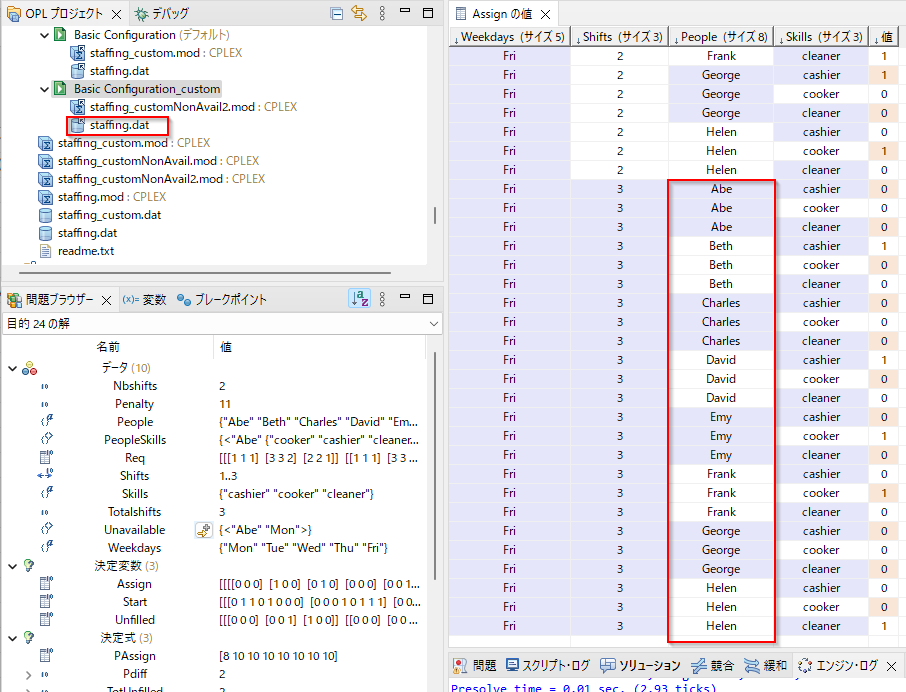
複数の競合した制約がありますが、ここでは、制約７で競合が起きていて、Abeが水曜日に休まなければ、競合が起きないことに注目してみます。

image.png

では、ここではデータを修正して、Abeが水曜に休むというデータUnavailable = {<Abe, Wed>};を削除しUnavailable = {};にしてみます。
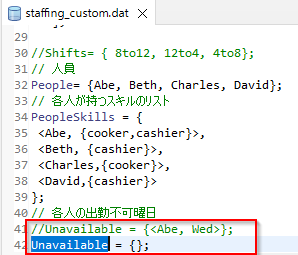
image.png

再度求解すると、今度は競合がなくなり、実行可能解、最適解が得られました。
Abeが水曜日に出勤していることがわかります。
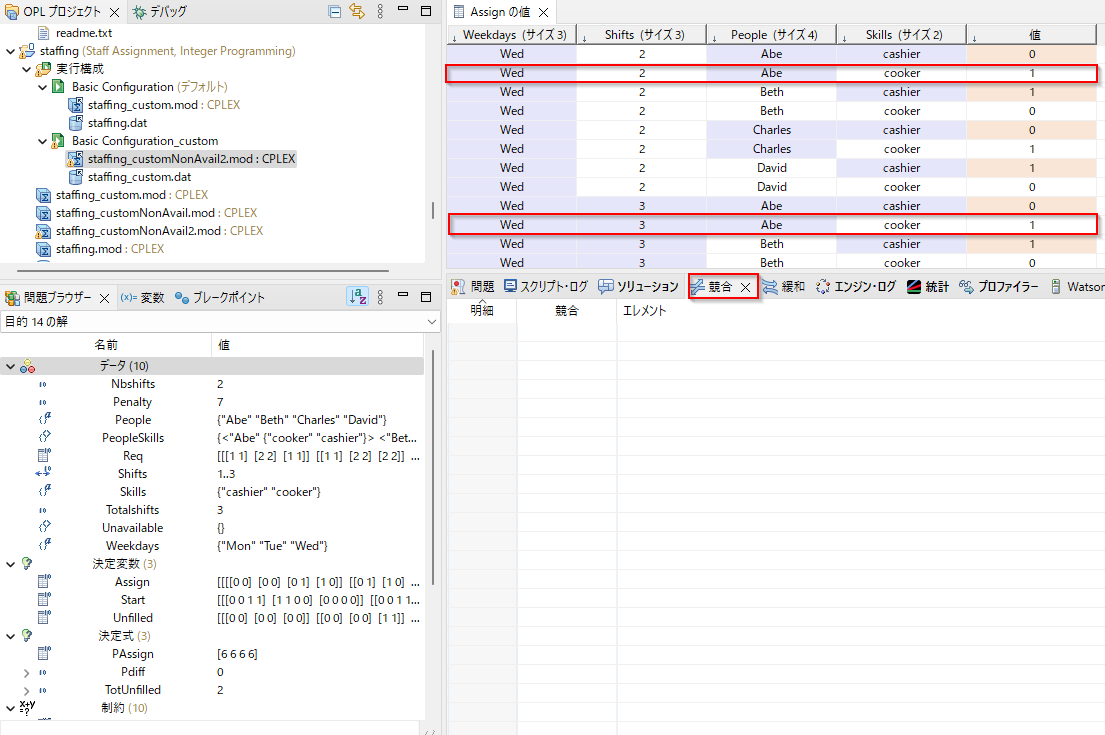
image.png

このように競合した制約を確認し、制約を緩和したり、データを修正することで、実行可能解を探していくことができます。

おまけ. スタッフや曜日の数が増えた場合

この元々のサンプルのstaffing.datファイルでは、スタッフが8名、月ー金までの曜日が定義されています。
このdatファイルで実行してみた結果が以下です。8名のスタッフのシフトが作成されています。

image.png

参考

人材割り当て問題 - IBM Documentation

CPLEXサンプルを読み解く記事一覧

3
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
3
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?