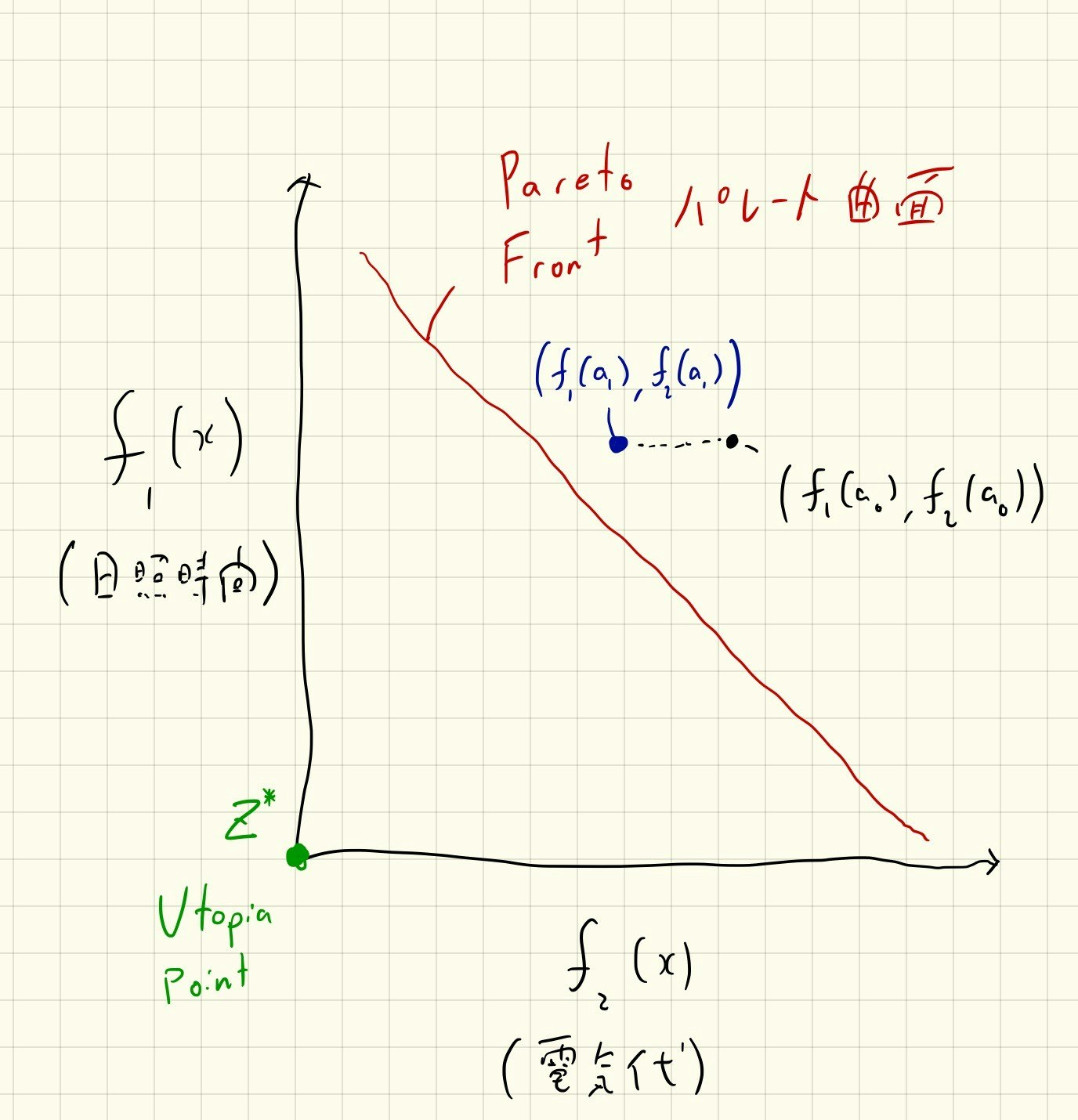はじめに
こんにちは、sp4ghetです。
本記事は Kichigai-Friends Advent Calendar 2017の14日目の記事になります。
高卒留年休学系の崖っぷち人生の友人同志でこじんまりとやっている Slack のみんなでアドベントカレンダーをやろうということなのでテーマに一貫性はないと思われます。
そして本記事は自分で書いた英語記事の日本語訳(自由型)です。
読者の前提知識は高校数学以上のことをほとんど仮定していないのでアドベントカレンダー読んでる人ならば基本的に問題ないと思います。読み終わった頃には多目的最適化やその周辺概念を雰囲気で理解できていると嬉しいです。
逆に、有識者の方々には間違いがあればバシバシ言って欲しいです。
網羅的な説明をすると日が暮れるので連続最適化問題の多目的ケースをParticle Swarmで最適化することをゴールに説明していきます。
最適化とは
多目的最適化について話す前に、まず「普通の」最適化について説明しないといけません。
最適化というのは目的関数の引数を調節して目的関数の値(出力)を最小化することを指します。
数式で書くと、
$$ min\ f(x) $$
となるような$x$をみつける行為を最適化といいます。
かなり簡単な例でいくと、目的関数が二次の多項式のケースを考えていきます。
$$ f_1(x) = x^2\ where\ x \in \mathbb{R}^1$$
この関数の最小値は $x$ が0のとき0になります。
とりあえずこの関数は簡単ですね。最適化できました。
ここではじめて登場する$where\ x\in\mathbb{R}^1$というのはxが実数であるということを示します。
$\mathbb{R}^n$ はn次元のユークリッド空間というものを指します。ユークリッド空間というと難しく聞こえますが、 $\mathbb{R}^1$は線のような1次元で、$\mathbb{R}^2$ は学校の数学でよく扱うグラフを書いたりするような2次元です。$\mathbb{R}^2$ のときの引数 $\vec{x}$ は
$$\vec{x} = (x_1, x_2)$$
といったように二次元になるだけの問題です。
最適化アルゴリズム
この関数を例にもっとも簡単な 「勾配降下法」 と呼ばれる 最適化アルゴリズム を紹介したいと思います。
最適化アルゴリズムというのは最適化を行うための手順のことを指していて、一般的にはコンピュータープログラムに落とし込んで実行可能にします。
勾配降下法のイメージとしては、ボールが坂を転がる様子に似ています。
要するに言いたいこととしては「傾き(勾配)」を計算してそれを「降下」していきたいんです。
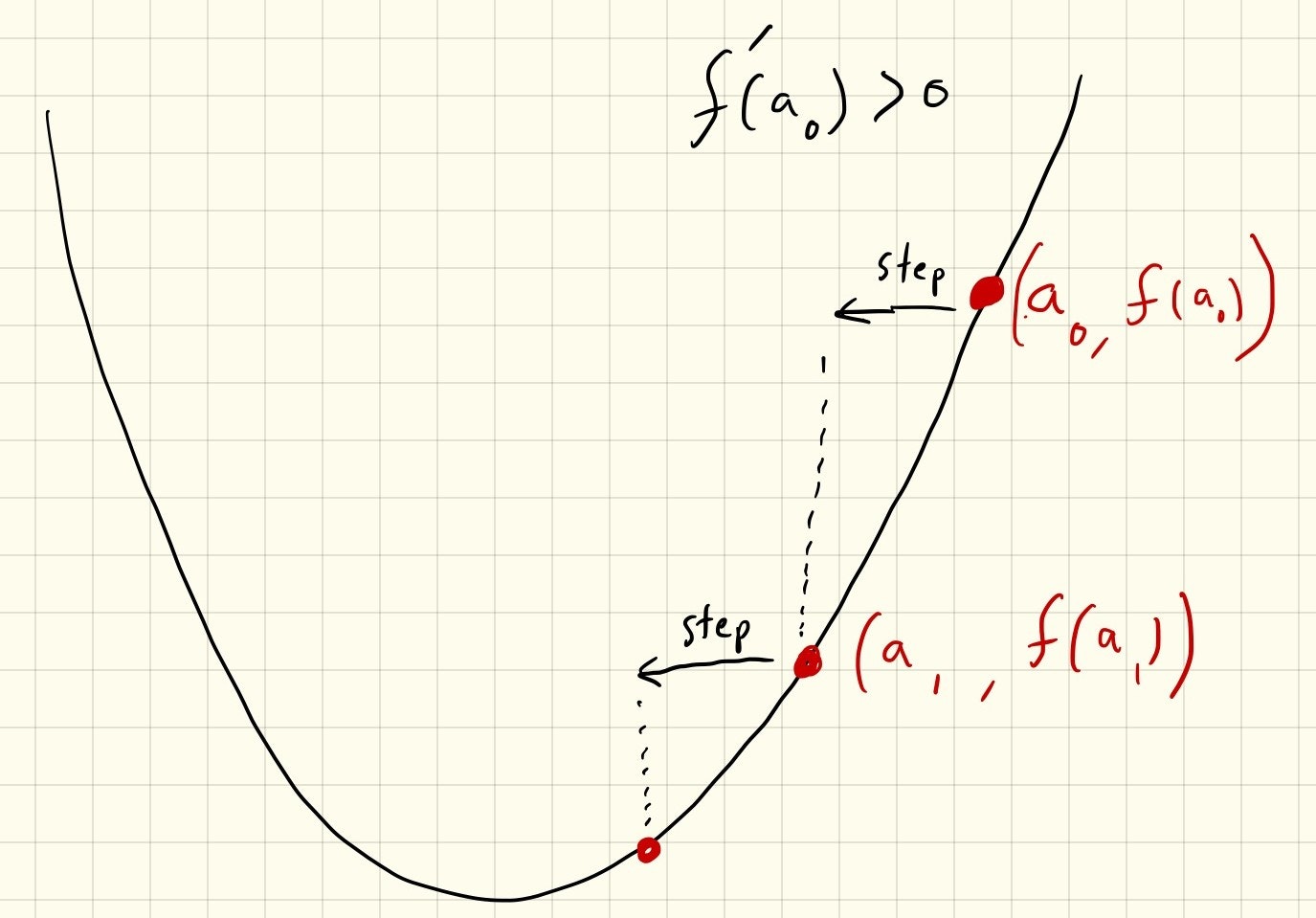
- ランダムな引数 $a_0$ を $\vec{x}$ に代入して、
- 目的関数 $f(\vec{x})$ を微分します (ベクトル解析という数学の分野では多次元に対応する微分とよく似た勾配という概念を使います)。
- その微分した結果(勾配)と逆の方向に $\vec{x}$ を一定距離 $step$ 分動かします。 逆方向に進む理由は最小化を行っているので、傾きの反対方向に進むためです。
- 2-3の手順を何度か繰り返します。終了条件は事前に決めてあるループ回数、しばらくの間値が変化しない場合に終了するなどと比較的自由です。
結果的に $step$ の大きさに応じて最小値の0に収束するか0の周りを振動しますね。
ちなみにこの勾配降下法とその亜種は非常に素早く収束するため機械学習で活躍しているので勾配降下法の奥深さは侮れないです。
詳しくなりたい人はこの記事がオススメです: 勾配降下法の最適化アルゴリズムを概観する
局所解
ただし、我々が考えたナイーブな勾配降下法には欠点があります。
たとえばこの関数を例にとってみましょう。
$$ f_2(x) = x^4-2x^3-x^2+x $$
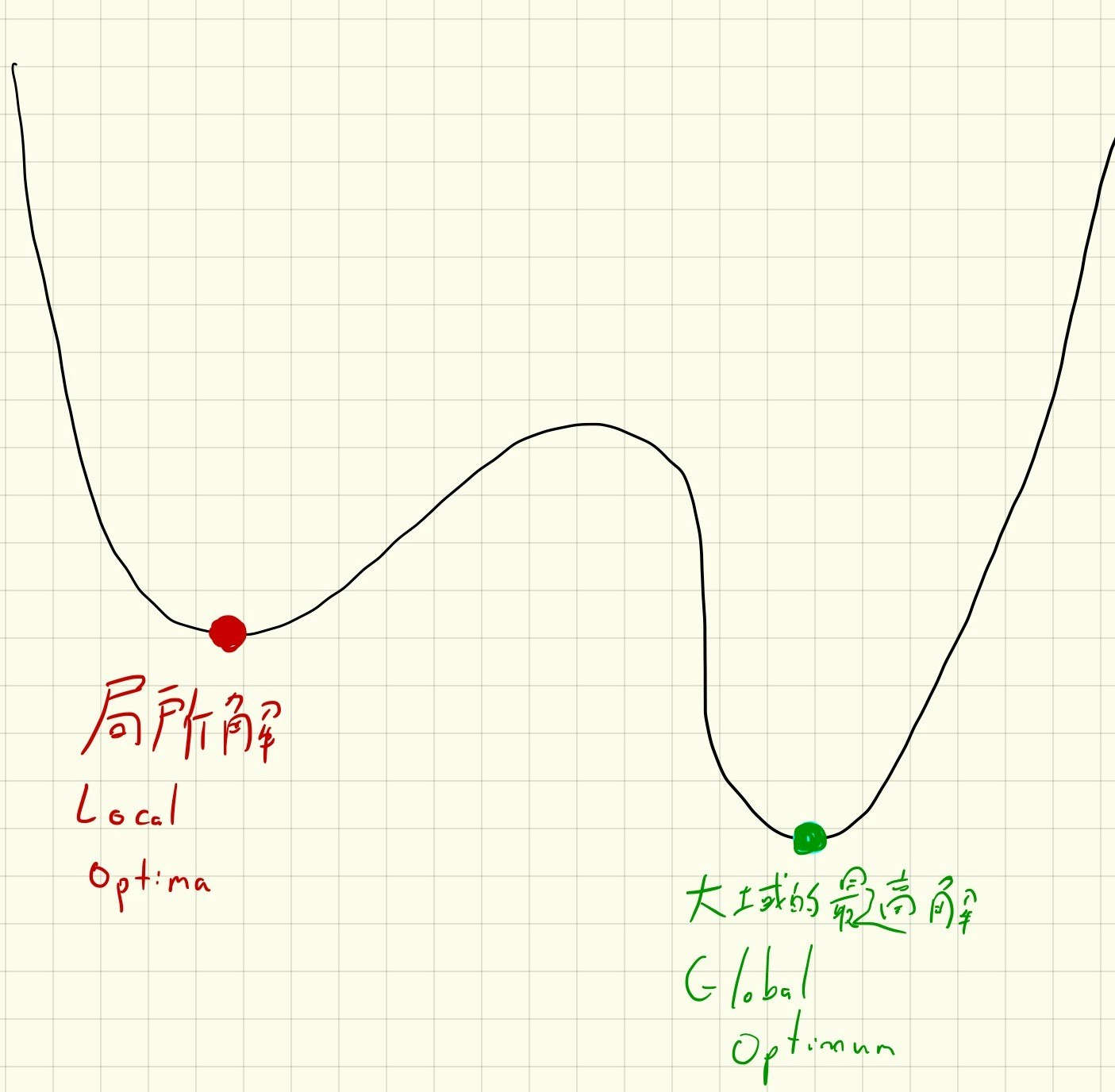
もし最初に $x=-100$ と代入して、転がり降りた先の小さな谷に収束したとしても、より深い谷が他にも存在しますね。
このような小さな谷のことを 局所解(Local Optima) と呼びます。このように最適化アルゴリズムが 大域的最適解(Global Optimum) に収束しなかったときのことを「局所解に陥る」といいます。
最適化アルゴリズムは局所解に陥らないで素早く収束することを目的にしていますが、その両立は難しいです。
「素早く」というのは、目的関数の評価回数を少なくするという意味でもあります。$\vec{x}$ がとりうる値すべてに対して目的関数を評価して結果が良かったものを選択してしまえば最適解は得られるので、いかにして評価回数を抑えつつ最適化するかが味噌だったりします。
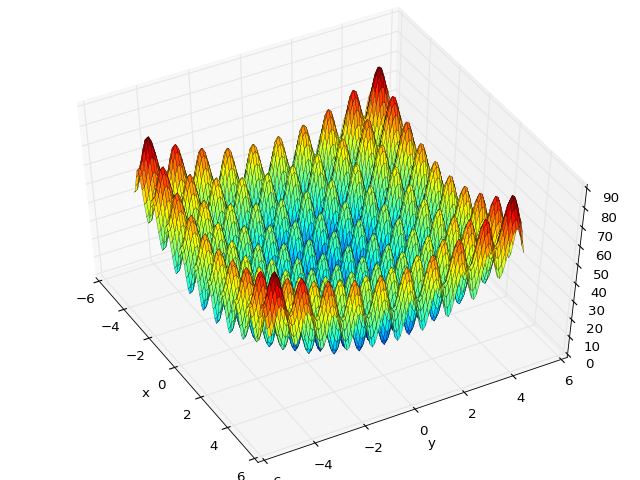
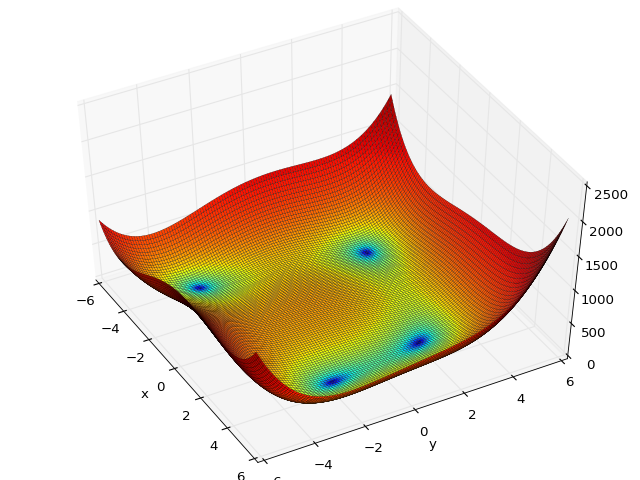
ちなみに、最適化アルゴリズムの評価に使われる評価関数はかなり複雑な構造をしていたりするので興味深いです。
このページにさまざまな評価関数が載っています。
最適化問題の分類
そろそろ多目的最適化にたどり着くまであと1歩のところに来ました。
今までの目的関数では引数は多次元でしたが、大域的最適解はひとつに限定されていて目的関数の値も実数でした。
最適化問題を目的関数の数と、最適解の数で分類していきましょう。
こういった最適化問題は 多峰性(Multimodal)最適化問題 と呼びます。
さらに、引数の次元だけでなく目的関数も複数になると 多目的(Multiobjective)最適化問題 になります。
例として「窓の大きさ」とを引数にしたときの「日照時間」と「電気代」を目的関数にしたときの最適化問題などがあげられます。
日照時間などの多くあるほうが嬉しい量に関しては符号を反対にしてしまえば最小化問題として扱えます。
数式で表現すると、こんな感じです。
$$
\mathbb{F}(\vec{x}) = {f_1(\vec{x}), f_2(\vec{x})...f_n(\vec{x})}\ where\ 1 < n < 4
$$
さらに、目的関数が4つ以上ある場合は 多数目的(Many-objective)最適化問題 と呼ばれます。
さっきの$n$が4より大きい場合のことですね。
$$
\mathbb{F}(\vec{x}) = {f_1(\vec{x}), f_2(\vec{x})...f_n(\vec{x})}\ where\ n \geq 4
$$
| 問題の種類 | 目的関数の数 | 最適解の数 |
|---|---|---|
| Normal Fitness Function | $1$ | $1$ |
| Multimodal (多峰性) | $1$ | $n \geq 2$ |
| Multiobjective (多目的) | $2,3$ | $n \geq 1$ |
| Many-Objective (多数目的) | $\geq 4$ | $n \geq 1$ |
多目的になったときの問題
目的関数がふたつになったからどうした、と思われるかもでしれませんがそれなりに影響が出るようになります。
先ほどの「窓の大きさ」を引数とした「日照時間」と「電気代」の最適化問題をみてみましょう。
日照時間に対して最適化していくと理想的には壁や屋根もすべて窓にしたくなります。
次に電気代に対して最適化すると、窓がひとつもない壁や屋根がすべて断熱材になってしまいます。
「日照時間」と「電気代」は トレードオフ の関係にあります。どちらかがよくなるともう片方はわるくなります。
これは「窓の大きさ」という共通の引数による影響が複数であることから発生する問題です。
実際に家を建てるときについて考察してみると、たいていの家に窓がついてますが、壁がすべて窓というケースは稀です。
つまり、もっとも最適な窓の大きさは日照時間と電気代のそれぞれの最適ではなく間にある何かなのです。
いままでは目的の関数の値がひとつの実数だったので自然と「よさ」を定量化できました。多目的最適化問題では別の「よさ」を定義します。
まず、 読みやすさのために引数である窓の大きさを $\vec{x}$, 目的関数の日照時間を $f_1(\vec{x})$, 電気代を $f_2(\vec{x})$ と表します。さらに、多目的最適化問題そのものは $\mathbb{F}(x) = {f_1(\vec{x}), f_2(\vec{x})}$ と表します。
x軸を $f_1$ の値、 y軸を $f_2$ の値にしたグラフを書いたとき、すべての目的関数が最小値をとる、 $(min\ f_1(\vec{x}),min\ f_2(\vec{x}))$ となる点があります。この点のことを 理想点(Utopia Point) と呼び、 $\mathbb{Z}^*$ と表現します。窓の例をとると日照時間が1日24時間かつ電気代が0のときです。多くの場合、先ほど挙げたトレードオフ関係のせいで理想点は実現することが不可能です。
勾配降下法と同じように,適当に $\vec{a}_0$ を選んで $\vec{x}$ を初期化します。別の値 $\vec{a}_1$ を $x$ に代入したとき $f_1(\vec{a}_0)=f_1(\vec{a}_1)$ で $f_2(\vec{a}_0)>f_2(\vec{a}_1)$ の場合があるとします。 このときはトレードオフが発生しないので $a_1$ のほうが「よい」と言い切れます。 このような状況について $\mathbb{F}(\vec{a}_1)$ は $\mathbb{F}(\vec{a}_0)$ を 支配(Dominates) するといいます。
厳密にはすべての目的関数について $f_i(\vec{a}_0) \geq f_i(\vec{a}_1)$ が成立し、最低でもひとつの目的関数について $f_i(\vec{a}_0) > f_i(\vec{a}_1)$ が成立する場合に $\mathbb{F}(\vec{a}_1)$ は $\mathbb{F}(\vec{a}_0)$ を支配します。
引数 $x$ が取りうる値の範囲をすべて考慮したうえで支配されない、つまり「可能な限りよい」、点について パレート最適(Pareto Optimal) であるといいます。 そして、パレート最適な点が構成する境界を パレート最適曲面/曲線(Pareto Front) と呼びます。
多目的最適化問題はこのパレート最適曲面をみつける問題です。
多目的最適化問題の評価関数もかなり複雑な構造をしたものがいくつかあります。
僕は多目的最適化問題のグラフを理解するのにひっかかったのですが、$f_1$ と $f_2$ を$x$を媒介変数として媒介変数表示しています。高校数学でやりましたね。ちょっと頭の中でしっくりくるまで時間かかりました。
Wikipediaにいくつか多目的最適化の評価関数が載っていますのでオススメです。
多目的最適化アルゴリズム
さて、実際に多目的最適化問題を解くにはどうすればいいのでしょう。
さまざまな多目的最適化アルゴリズムが存在しますが、有名なものでは遺伝的アルゴリズムなどがあります。今回は遺伝的アルゴリズムよりシンプルな Particle Swarm Optimization(PSO) を用いた多目的最適化を行っていきます。
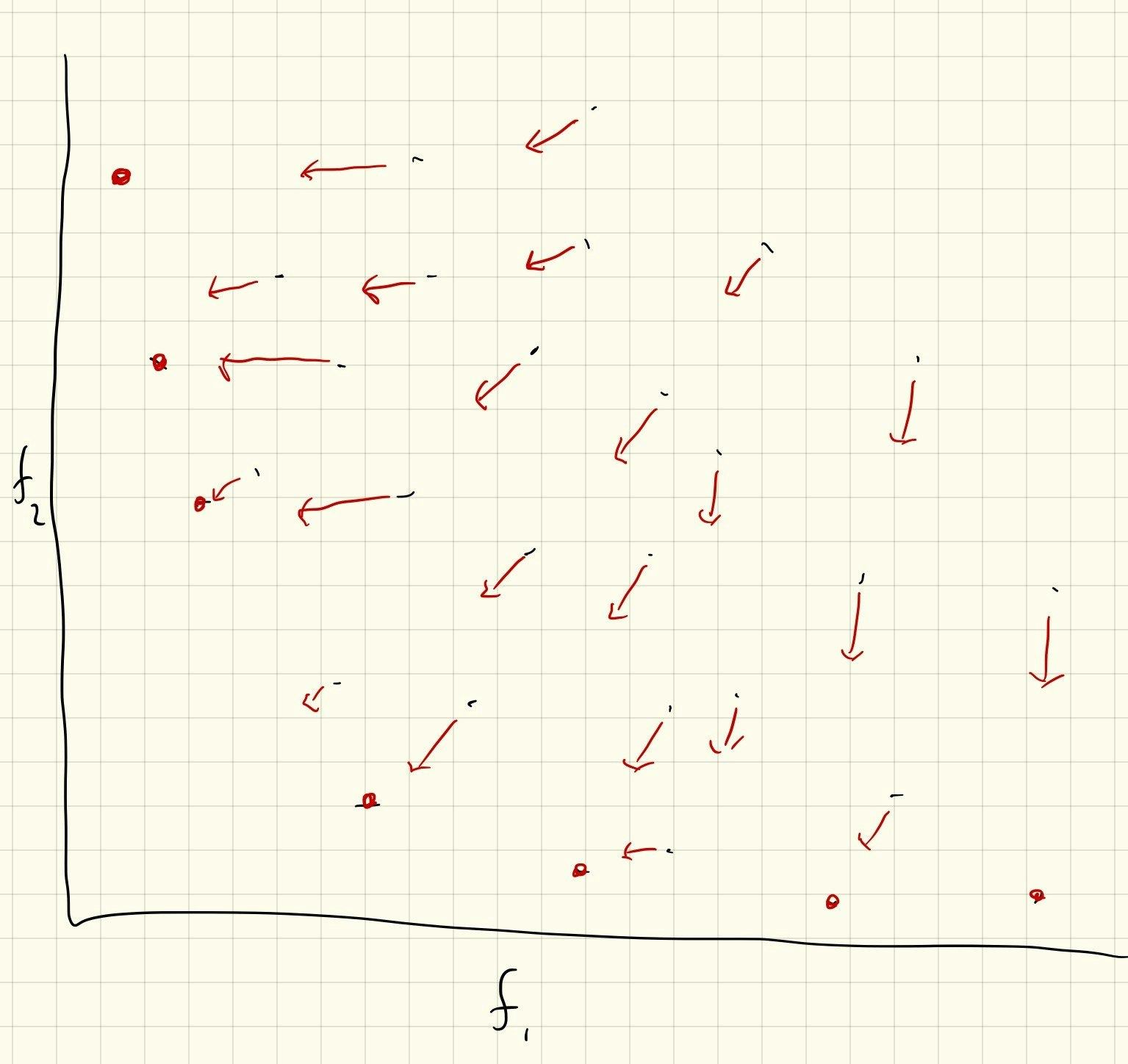
PSOのイメージとしては、鳥の群れが協力して最適解を探す感覚に似ています。
伝われ!(笑)
- $\vec{x}_i(0)$ と $\vec{v}_i(0)$ を $M$ 個用意してランダムなベクトルで初期化します。 $\vec{x}_i$ がひとつのParticleで、 $\mathbb{F}(\vec{x})$ の引数と同じ次元数です。 Particleの群れ $X$ をSwarmと呼びます。
- $\vec{v}_i(1)$ を計算します。 $\vec{v}_i(t)$ は時間 $t$ のときの $x_i$ の速度です。ここが味噌で少し長くなるので後で詳しく説明します。
- $\vec{x}_i(t+1) = \vec{x}_i(t)+\vec{v}_i(t)$ という式に沿ってParticleの位置を更新していきます。
- $\mathbb{F}(\vec{x}_i)$ を計算して、歴史上支配されていないParticleが最新のパレート最適曲面になります。
- 3-4 を何度か繰り返します。
肝心の $\vec{v}_i(t)$ の計算についてですが、まずParticleに対して慣性 $W\vec{v}_i(t-1)$ が働きます。
高校の物理基礎とかでやる力学に出てくるあれです。過去の速度が $0 < W < 1$ 倍になっている状態です。
次に各Particleは今まで通ってきた経路上にある目的関数の支配されていない位置がどこにあったかの記憶 (Personal best $pbest$) を保持しています。さらに、現在の群れ全体の支配されていないParticleの位置に関する情報 (Global Best $gbest$) も共有されています。
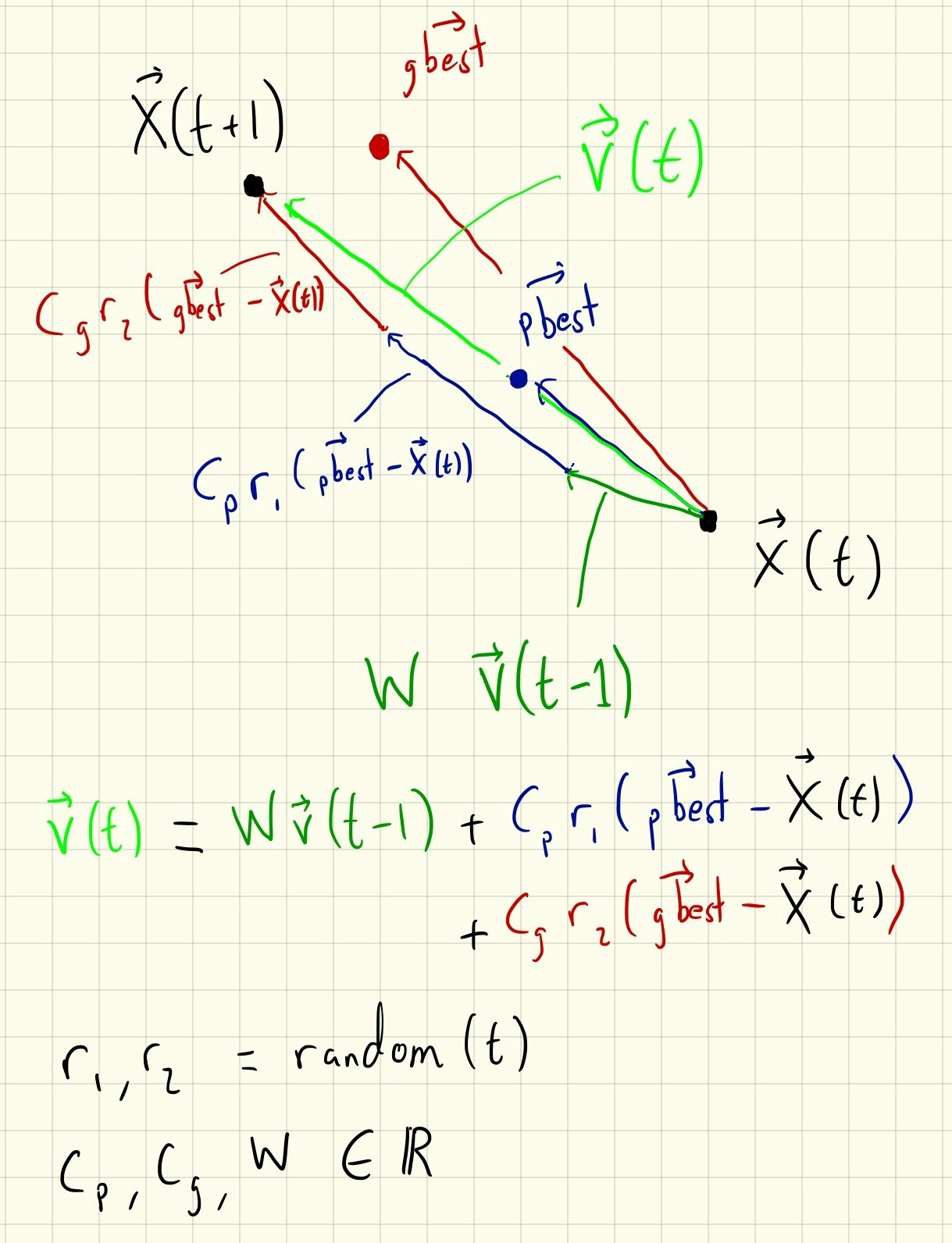
支配されていない位置は複数あるかもしれないので、$pbest$ と $gbest$ からそれぞれランダムにひとつのベクトルを選びます。それらと現在位置の差のベクトルを係数 $0 < C_p, C_g < 1$ とランダムな正数 $r_1, r_2 < 1$ でそれぞれ掛けて大きさを整えます。慣性ベクトルとこのふたつのベクトルを足し合わせることによって新しい速度ベクトル $\vec{v}_i(t)$ が求められます。
数式で表現すると:
$$
\vec{v}_i(t) = W\vec{v}_i(t-1) + C_pr_1(\vec{pbest}_i - \vec{x}_i) + C_gr_2(\vec{gbest} - \vec{x}_i)
$$
です。
係数やParticleの数の $W, C_p, C_g, M$ はアルゴリズムの ハイパーパラメタ と呼ばれるアルゴリズムの動きをチューニングするのに用いられる変数で、実行前に決めておく値です。 $r_1, r_2$ は $t$ が変化するとランダムに変化する乱数で、より万遍なくParticleが飛び回ることを促すためにあります。
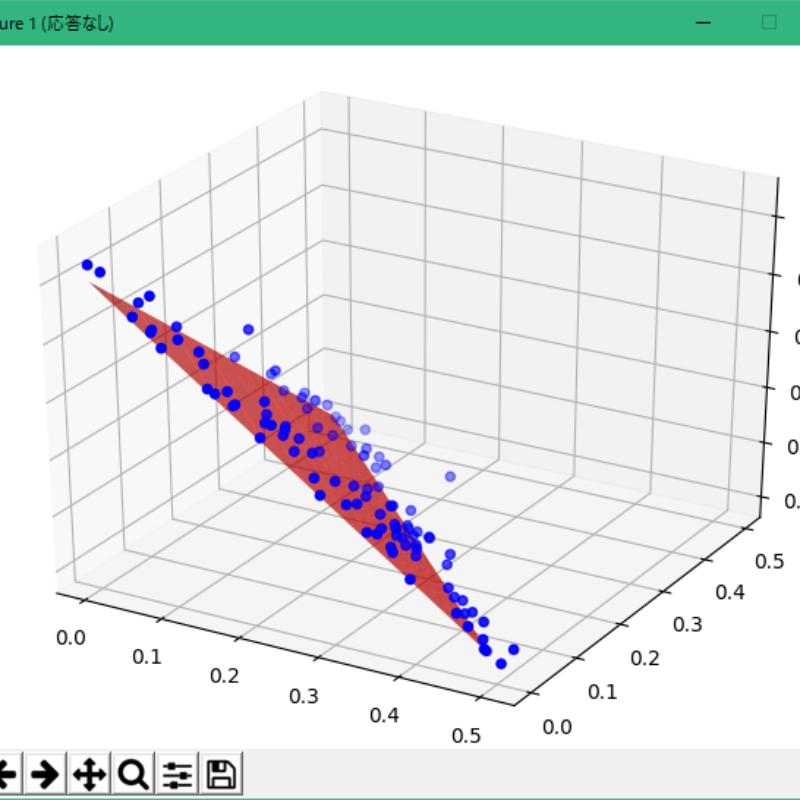
多目的最適化アルゴリズムの評価関数のひとつであるDTLZ-1という関数に対してこの多目的PSOを実行した結果を可視化するとこのようになります。
赤い面が真のパレート最適曲面です。青い点がそれぞれひとつのParticleです。
以上で最適化、多目的最適化問題、多目的最適化アルゴリズムへの入門が完了したつもりなのですが、いかがでしたか?
実際に実装するときはもう少し複雑な内容になるのですが、そこが気になる人は多目的PSOのソースコードをここに貼ったので読んでみてください。 時間の都合で実行できるフォーマットじゃないのですが近いうちにコードをきれいにしてリポジトリをまとめておきます。
入門の次
遺伝的アルゴリズムを用いた多目的最適化アルゴリズムに興味がある方はこの論文 A fast and elitist multiobjective genetic algorithm: NSGA-II がオススメです。そして宣伝ですが、NSGA-IIを実装したのでよかったら見てください。こっちは実際に実行できます。
また、例として挙げていた窓の大きさを使った多目的最適化問題は BPOpt: A Framework for BIM-Based Performance Optimization.で実際に扱われています。
多目的最適化はこの記事で紹介しきれるほど小さい分野ではないので Survey of Multi-objective Optimization Methods for Engineering. やMulti-Objective Particle Swarm Optimizers : A Survey of the State of the Artなどのサーベイペーパーから流し読みしていくのがオススメです。