はじめに
ずっと有限要素法を使って構造計算をやってきた@soy_botです.
最近,時系列解析をする仕事が多く,道具としてフーリエ解析,複素解析を使うことがあります.
特に,高速フーリエ変換(Fast Fourier Transform, FFT)については使用頻度が多いので,勉強を兼ねて実装して遊んでいます.
そんな中,ボスから,FFTで微分方程式を解くスペクトル法なるものがあると聞き,たまたまラボにテキストが落ちていたので実装して遊んでみることにしました.
石岡先生のスペクトル法のテキストで勉強しています.
https://www.amazon.co.jp/%E3%82%B9%E3%83%9A%E3%82%AF%E3%83%88%E3%83%AB%E6%B3%95%E3%81%AB%E3%82%88%E3%82%8B%E6%95%B0%E5%80%A4%E8%A8%88%E7%AE%97%E5%85%A5%E9%96%80-%E7%9F%B3%E5%B2%A1-%E5%9C%AD%E4%B8%80/dp/4130613057
ですので,この記事の内容は,本テキストの3章くらいまでの内容に沿ったものになります.
詳細な説明は本テキストをご参照ください.
以下はその備忘録です.
スペクトル法についてはあくまで素人ですので,誤りなどもあろうかと思います.ご指摘頂ければ幸いです.
スペクトル法とは?
微分方程式の近似解法のうち,基底関数にフーリエ級数やチェビシェフ多項式等の周期関数を用いるものの総称と理解しています.微分方程式初期値境界値問題をFFTを実行することに帰着させることで,特定のクラスの問題に対して極めて高精度かつ高速に求解できる特徴があります.
また,適切な基底関数を用いることで,エネルギーや運動量,位相速度を厳密に保存できる特性もあり,優れた解法です.
1次元線形移流方程式
\frac{\partial u(x,t) }{\partial t} + c \frac{\partial u(x,t) }{\partial x} = 0
このように表せる微分方程式です.
今回は,簡単のため以下の初期条件および境界条件を設定します.また,移流速度cは簡単のため1とします.
(ご指摘頂きありがとうございました.)
u(x,0) = f(x) \hspace{1cm} (0 \le x \le 2 \pi)
u(x,t) = u(x +2 \pi, t)
スペクトル法による解法
まず,未知関数であるu(x,t)を以下のように離散フーリエ近似します.
u(x,t) = \sum_{-N}^{N} \hat{u}_{k}(t) {e}^{ikx}
また,残差Rを次式により与えます.
R = \frac{\partial u(x,t) }{\partial t} + \frac{\partial u(x,t) }{\partial x}
この残差に,近似式を代入し,重みwをかけて領域全体で積分すると,次式を得ます.
\int_{0}^{2 \pi} \sum_{-N}^{N} w\frac{\partial \hat{u}_{k}(t)}{\partial t} {e}^{ikx} + \sum_{-N}^{N} \hat{u}_{k}(t) w \frac{\partial {e}^{ikx} dx}{\partial x} = 0
また,重みに次式を用いることで,
w = e^{-ikx}
重み付き残差式は以下のようになります.
\int_{0}^{2 \pi} \sum_{-N}^{N} \frac{\partial \hat{u}_{k}(t)}{\partial t} + \sum_{-N}^{N} ik \hat{u}_{k}(t) dx= 0
この式を整理し,三角関数の直交性を用いることで,次式が得られます.
\frac{\partial \hat{u}_k (t)}{\partial t} + ik\hat{u}_k(t) = 0
これは,スペクトルの時間発展を支配する常微分方程式となります.ここは感動しました.
ですので,あとは初期値を離散フーリエ変換して初期スペクトルを得て,その時間発展を上記の微分方程式に従い解けば,任意の時刻におけるフーリエスペクトルを得ることができます.
具体的には,
\hat{u}_k(0) = \frac{1}{2 \pi} \int_0^{2 \pi} f(x) e^{-ikx} dx
として,初期スペクトルを求め,
上記の常微分方程式に放り込んで計算することで,以下の式を得ます.
\hat{u}_k(t) = \hat{u}_k(0) e^{-ikt}
あとは,時間ごとにこのフーリエスペクトルを逆離散フーリエ変換することにより,近似解を得ることができます.
u(x,t) = \sum_{k=-N}^{N} \hat{u}_k(t) e^{ikx}
なお,フーリエスペクトルの時間発展に関する厳密解に着目すれば,この式は次式に書き改められます.
u(x,t) = \sum_{k=-N}^{N} \hat{u}_k(0) e^{-ikt} e^{ikx} =\sum_{k=-N}^{N} \hat{u}_k(0)e^{ik(x-t)}
これは,離散化に用いた全ての振動数に対して,その位相速度が厳密解と同じ1となることを意味します.
ちなみに,中心差分で近似した場合はそうならず,高周波成分の位相速度が遅れます.詳しくはテキストをご参照ください.
Fortranによるコード
では,具体的な計算に入ります.
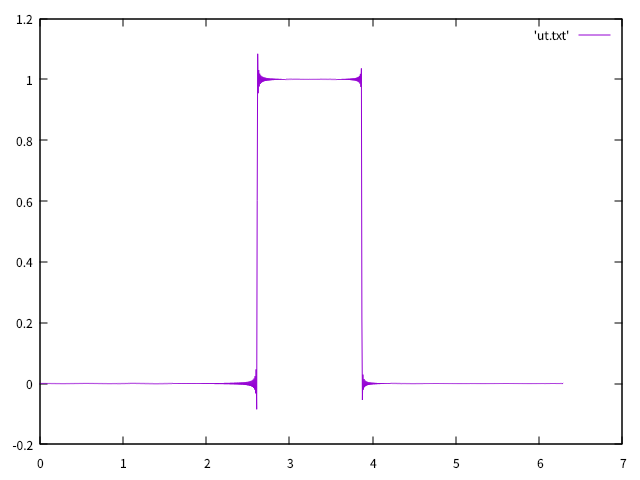
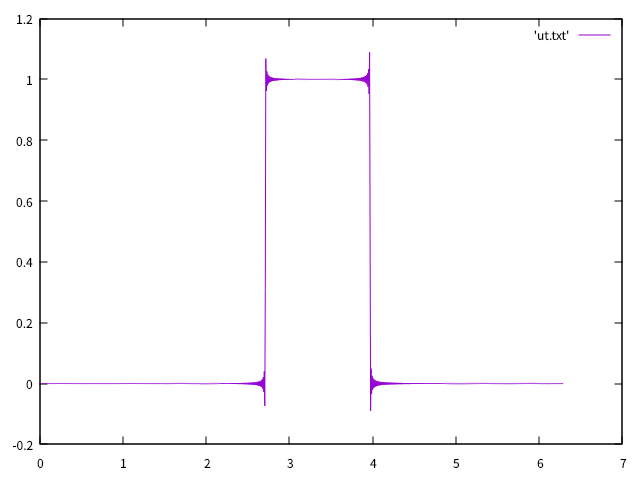
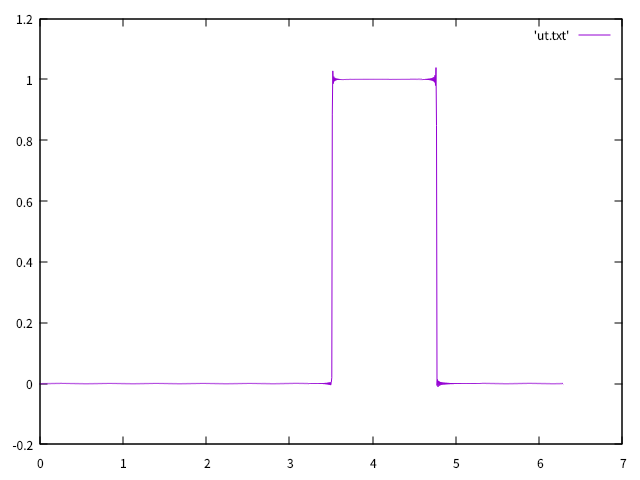
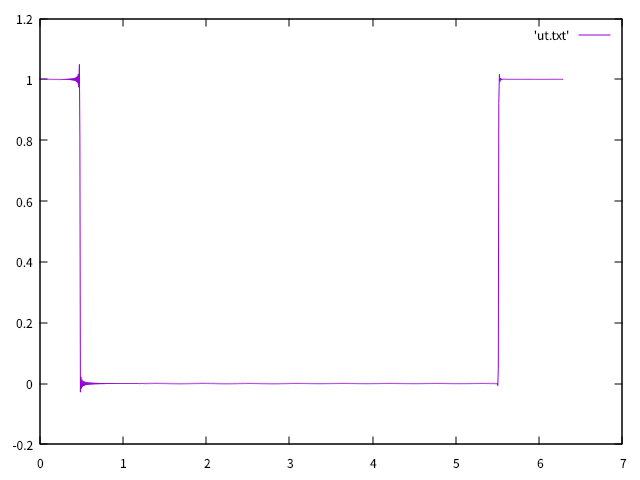
矩形波を初期値としたらどうなるか気になったのでやってみました.
要は,
(1) 初期値を離散フーリエ変換して,フーリエスペクトルを求める.
(2) 時間発展方程式
\hat{u}_k(t) = \hat{u}_k(0) e^{-ikt}
(参照する式が違いました。ありがとうございます。)
により未来のフーリエスペクトルを求める.
(3) 逆離散フーリエ変換により,u(x,t)を求める.
ということになります.
以下のような矩形波のフーリエスペクトルを,今回は検証のため手計算で求めました.
f(x) = 1 \hspace{1cm} \left(\frac{4}{5}\pi \le x \le \frac{6}{5} \pi \right),
f(x) = 0 \hspace{1cm} \left(otherwise \right)
すると,こんな関数が得られます.
\hat{u}_k(0) = \frac{1}{\pi k} {e}^{-ik\pi} {\rm sin}\frac{\pi}{5}k
あとは,コード上で(1),(2)および(3)を実行するだけです.
program main
use plantfem
implicit none
integer(int32) ,parameter:: N = 2**9
complex(real64),allocatable :: x(:),uk0(:),uk(:),ut(:)
integer(int32) :: i,k,j
real(real64) :: T
type(Math_) :: Math
type(IO_) :: f
type(Console_) :: console
! 初期時刻を0として,何秒後の解がほしいか.
call console%log("Input Time: T")
call console%read()
T = freal(console%line)
! (1) 離散フーリエ変換により,初期値のフーリエスペクトルを求める.
allocate(uk0(-N:N) )
do k=-N,N
if(k==0)then
uk0(k) = 1.0d0/Math%PI*exp(-Math%i*dble(k)*Math%PI )*Math%PI/5.0d0
cycle
endif
uk0(k) =1.0d0/Math%PI/dble(k)*exp(-Math%i*dble(k)*Math%PI )*sin(Math%PI/5.0d0*dble(k) )
enddo
! (2) ある時刻T後のフーリエスペクトルを求める.
allocate(uk(-N:N) )
do k=-N,N
uk(k) = uk0(k)*exp(-Math%i*dble(k)*T )
enddo
! (3) 逆フーリエ変換(by DFT)
x = linspace([0.0d0,2.0d0*Math%PI],2*N+1)
ut = zeros(2*N+1)
do i=1,size(x)
do k=-N,N
ut(i) = ut(i) + uk(k)*exp(Math%i*dble(k)*x(i) )
enddo
enddo
! 出力
call f%open("ut.txt","w")
call f%write(real(x),real(ut))
call f%close()
call f%plot(option="with lines")
end program
ギブズ現象に起因するovershoot/undershootがみえますが,エネルギー,運動量,位相速度は保存されています.
ただし,今回用いたDFTでは遅いので,通常はFFTを用います.
ここで,今回は波数が2*N+1ありますが,通常のFFTでは2^Nで行うので,少し工夫が要ります.
この,FFTを使ったバージョンについては,また折をみて投稿します.
さいごに
今回のサンプルコードでは,Fortranの機能に加えて,独自拡張機能を入れています.
これらの機能はplantFEMをインストールすると使えます.是非使ってみてください!!
それでは,よきFortranライフを!