シンセサイザー作る

ステイホームなので

GW期間中は趣味に関することでもやろうかなと思い立ち、昔趣味でやっていたシンセサイザーをソフトで実装してみることにした。
信号処理とかは、ずぶのど素人なので、色々へんな実装しているかも。
ちなみに好きなメーカはKORG。音作りの幅が非常に広いエンジンを積んでいる事が多い。

減算シンセサイザーの基本構成

コンポーネント	役割
VCO	ボルテージ・コントロール・オシレータ。電圧を加えると、ピッチ（音程）の異なる波（音色）を出す。
VCF	ボルテージ・コントロール・フィルター。電圧を加えると、特定の周波数のみ通過させる。（音色を変化させる）
VCA	ボルテージ・コントロール・アンプリファイア。電圧を加えると、音量を変える。
LFO	ロー・フリケンシー・オシレータ。低周波数のオシレータ。VCOにかければ、ビブラート。VCFにかければオートワウ。VCAにかければトレモノになる。
ADSRエンベロープ	Attack,Decay,Sustain,Releaseで時間的変化をVCOやVCF、VCAにかける。
エフェクター	リバーブやオートパンなどの空間系、ディレイなどの時間変化系、オーバドライブ・トレモノ・コンプレッサなどの音量変化系、コーラスなどの音程変化系、ワウやイコライザなどの音色変化系など様々。

というのが、一番基本的な減算シンセサイザーのコンポーネント。
一般的にVCO => VCF => VCA => エフェクター の順番で信号が流れる。LFOやADSRは他のコンポーネントに変調をかける役割になる。

オシレーターを作る。

単位の型定義

object Synth{
  type Time = Double //時間単位
  type Amplitude = Double //波の振幅
}

波形の型

まずは、波形（信号）を表現してみる。波形とは時間（t）を入力すれば振幅（amp)を返す関数 amp = f(t)なので、ここまでは簡単。後々使いやすいように、四則演算を定義しておく。

// 「波形」を表す
trait Waveform {
  import Synth._

  def apply(time:Time):Amplitude

  def +(amp:Amplitude):Waveform = (time:Time) => this.apply(time) + amp
  def -(amp:Amplitude):Waveform = (time:Time) => this.apply(time) - amp
  def *(amp:Amplitude):Waveform = (time:Time) => this.apply(time) * amp
  def /(amp:Amplitude):Waveform = (time:Time) => this.apply(time) / amp

  def +(waveform:Waveform):Waveform = (time:Time) =>
    this.apply(time) + waveform(time)
  def -(waveform:Waveform):Waveform = (time:Time) =>
    this.apply(time) - waveform(time)
  def *(waveform:Waveform):Waveform = (time:Time) =>
    this.apply(time) * waveform(time)
  def /(waveform:Waveform):Waveform = (time:Time) =>
    this.apply(time) / waveform(time)
}

信号処理器の型

次にプロセッサーを定義。これは波形（信号）を入力し、波形（信号）を返す関数。各コンポーネント（VCOやVCFなど）はプロセッサーになる。

// 「信号処理」を表す
trait Processor {
 def apply(waveForm:Waveform) : Waveform
}

オシレータ関数

もっとも単純なサイン波を定義。周波数１のサイン波はSin(2πt)で表現できる。
FreqとGainは実装は一緒だが、常に一定の振幅を出し続ける波形。

object Waveform{
  val SineWave:Waveform = (time:Time) => Math.sin(Math.PI * time * 2.0)
  val Freq:Amplitude => Waveform = (amp:Amplitude) => (time:Time) => amp
  val Gain:Amplitude => Waveform = (gain:Amplitude) => (time:Time) => gain
}

オシレータは基本波形と周波数を受け取って、波形を返す関数。Oscillator関数に基本波形を入れると、周波数を受け取って波形を返す関数を返す。

object Processor {
  //波形を受け取りオシレーターを返す関数
  val Oscillator:Waveform => Processor =
    (waveform:Waveform) => (pitch: Waveform) => (time: Time) => waveform(time * pitch(time))

  // サイン波オシレータ
  val SineOsc:Processor = Oscillator(Wave.SineWave)
}

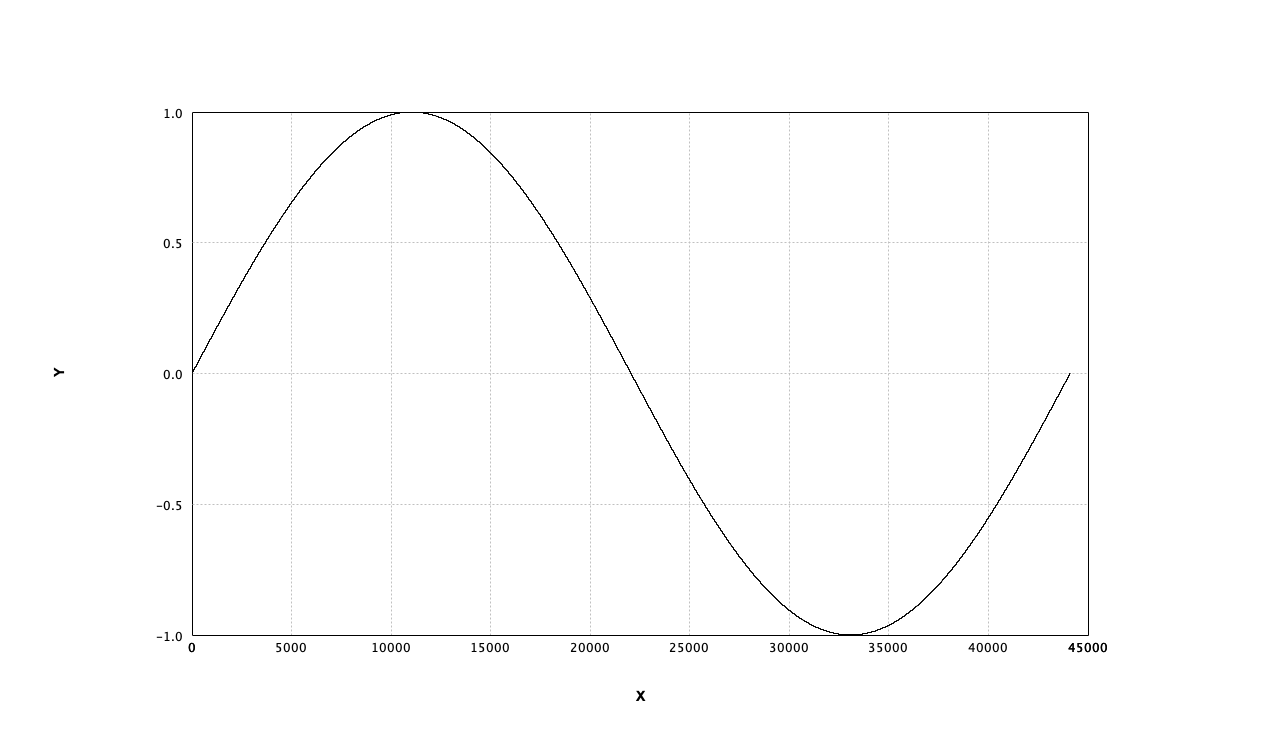
オシレータができれば周波数を低くすればすなわちLFOなので、とりあえずLFOでピッチを揺らすことができるようになった。

val lfo = SineOsc(Freq(2.0)) //低周波オシレータ
val osc = SineOsc(Freq(440.0) + (lfo * 2.0)) //ラの音（440Hz)ピッチをLFOで揺らす

音を鳴らす

波形だけ見てもなんなので、音を鳴らす。JDKではjavax.sound.sampledパッケージで音を鳴らす事ができるので、それを利用する。

波形を配列に変換し、再生する

class PCMContext(val bitDepth:Int,val sampleRate:Int) {
  def waveformToArray(waveform:Waveform,time:Double):Array[Short] =
    (0 until (sampleRate * time).toInt)
      .map(time => waveform(time.toDouble)) //振幅を計算し
      .map(_ * Short.MaxValue)  //16Bitに変換し
      .map(_.toShort)  //Short型にする
      .toArray

  def play(waveform:Waveform,time:Double):Unit = {
    import javax.sound.sampled._
    //サンプルレートとビット数、チャンネル数などを指定し
    val format = new AudioFormat(sampleRate,bitDepth,1,true,true)
    val line = AudioSystem.getSourceDataLine(format)

    //ラインにバッファを書き込む
    line.opne(format)
    line.start()
    val buff = this
      .waveformToArray(waveform,time)
      .flatMap(ByteBuffer.allocate(2).putShort(_).array())
    line.write(buff,0,buff.length)
  }
}

CD音源相当の16Bit(Short),サンプルレート44.1KHzで再生する。ちなみに人間の可聴域はおよそ20KHzであり、その２倍のサンプルレートがあれば可聴域の音を再現できる。

object PCMContext {
  implicit val Bit16_44K = new PCMContext(16,44100)
}

ついでに、Waveformにplayメソッドを生やしておく。

trait Waveform {
  //(中略）
  def play(time:Time)(implicit context:PCMContext) =
    context.play(this,time)
}

// ちょっとうるさいので、波に0.1をかけて音量を下げておく。
(osc * Gain(0.1)).play(1.0) 

フィルターを作る

シンセサイザーでよく使われるフィルタとしては

フィルタ	特徴
ローパスフィルタ(LPF)	特定の周波数以下の波だけ通過させる。
ハイパスフィルタ(HPF)	特定の周波数以上の波だけ通過させる。
バンドパスフィルタ	特定の周波数付近の波だけ通過させる。

減算シンセサイザーの場合はLPFを用いるので、これを実装する。
LPFはつまり高周波をなくすという事で、波の移動平均をとって、波形のギザギザをなだらかにすれば高周波部分は無くなる。

BiQuadフィルターの実装

デジタルフィルタの実装方法は、リンク先 を参考にしBiQuadフィルタを丸々真似した。移動平均を取るため、前回・前々回という状態が必要になる。より関数型っぽく再帰で書くべきかなーとも思ったけど、パフォーマンス悪そうなので、varなインスタンス変数（状態）を持つことにした。この辺はヘタレScalaラーです。

abstract class BiQuadFilter extends Processor{
  protected var in1,in2,out1,out2:Amplitued = 0.0
  var a0,a1,a2,b0,b1,b2:Double //このパラメータを色々いじる事で様々なフィルタになる

  def apply(waveform:Waveform) : Waveform = (time:Time) => {
    val in  = waveform(time)
    val out = (b0 / a0 * in)   +
              (b1 / a0 * in1)  +
              (b2 / a0 * in2)  -
              (a1 / a0 * out1) -
              (a2 / a0 * out2)
    //前回値の更新
    in2  = in1;  in1  = in;
    out2 = out1; out1 = out;
    out
  }
}

ローパスフィルタの実装

LPFはカットオフ周波数(freq)と、Q値（シンセサイザーでいうレゾナンス）をパラメータに取る。それぞれ、波形として入力ができるようにしておくことで、LFOなどでモジュレーションをかけられるようにしておく。

class LoPassFilter(val freq:Waveform,val Q: Waveform)(implicit context:PCMContext)
  extends BiQuadFilter {

  private var omega,alpha:Double
  override var a0,a1,a2,b0,b1,b2:Double = _

  override def apply(waveform:Waveform): Waveform = (time:Time) => {
    //各種パラメータを設定
    omega =  2.0 * Math.PI * freq(time) / context.sampleRate
    a0    =  1.0 + alpha
    a1    = -2.0 * Math.cos(omega)
    a2    =  1.0 - alpha
    b0    = (1.0 - Math.cos(omega)) / 2.0
    b1    =  1.0 - Math.cos(omega)
    b2    = (1.0 - Math.cos(omega)) / 2.0
    super.apply(waveForm)(time)
  }
}

オシレータと繋げる

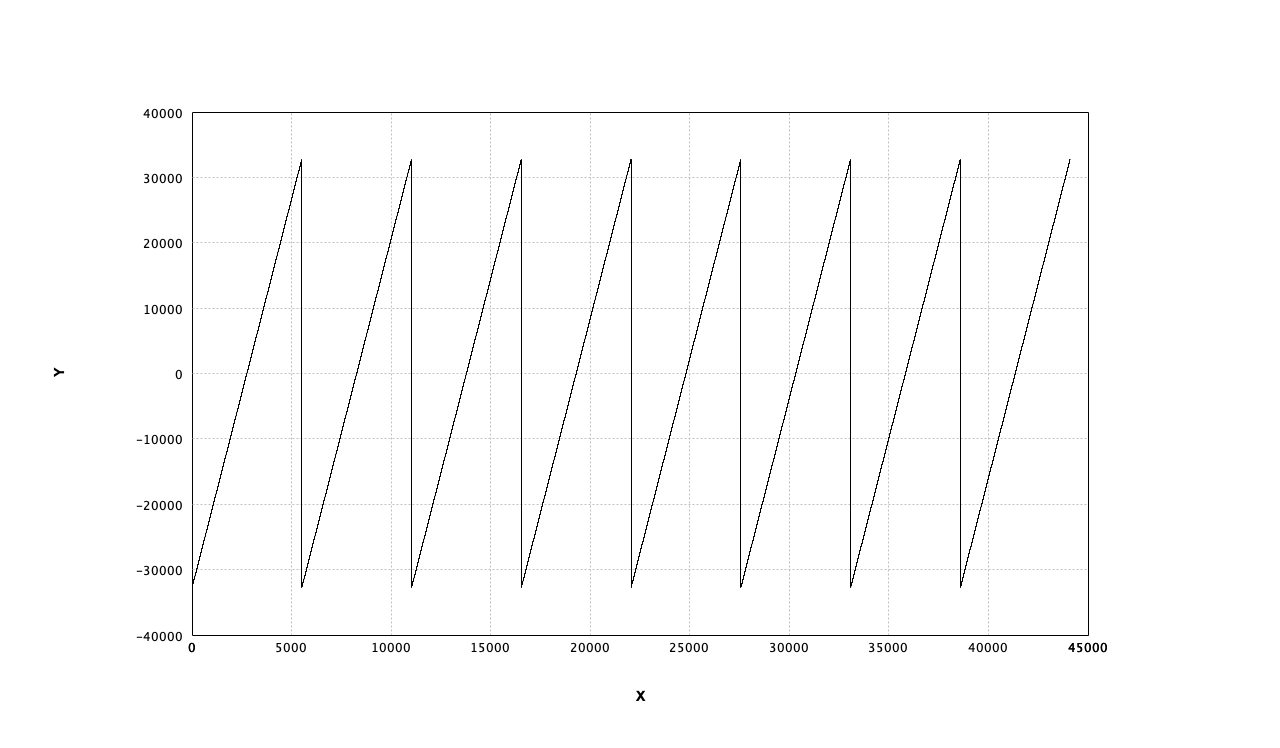
サイン波は倍音が含まれないので、ノコギリ波でフィルタを試してみる。

object Wabeform {
  //中略
  val SawWave:Waveform = (time:Time) => (time * 2.0) % 2.0 - 1.0
}
object Processor {
  //中略
  val SawOsc = Oscillator(Waveform.SawWave)
}

val osc = SawOsc(Freq(8.0))
val lpf = new LoPassFilter(Freq(16.0),Gain(1.0))

val out = lpf(osc) * Gain(0.1)
out.play(1.0)

フィルタなしノコギリ波（8Hz)

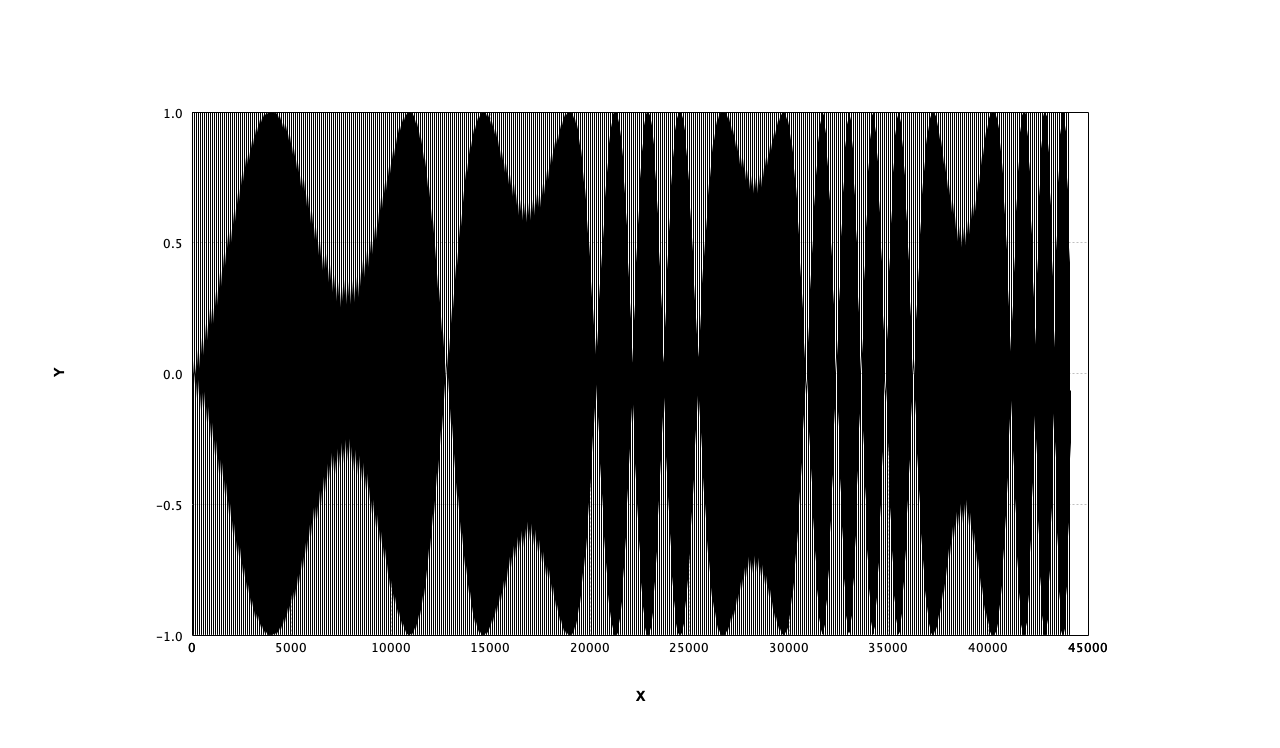
ローパスフィルタ(Cutoff 16Hz)後のノコギリ波(8Hz)

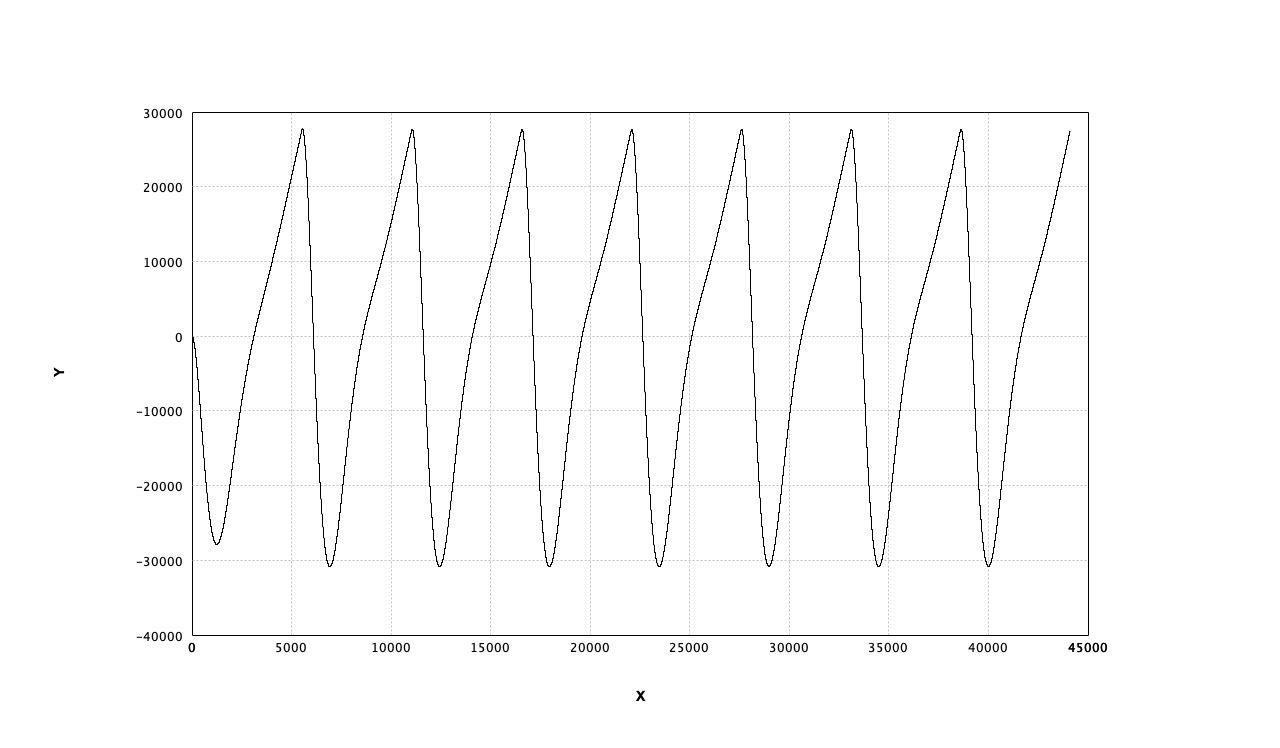
フィルタの前回入力の初期値がゼロなので、最初の山だけ低くなってしまっている。

アンプリファイア

基本

これまでもやってきたが、音量を調整するだけなら以下のように振幅を定数倍すれば良い。

val osc = SineWave(Freq(440.0))
val out = osc * Gain(0.5) //音を小さくする

ミキサー

複数の音を混ぜるのも、波形を足すだけで良い。

val osc1 = SawOsc(Freq(440.0)) * Gain(0.1)
val osc2 = SawOsc(Freq(220.0)) * Gain(0.1)
val osc3 = SawOsc(Freq(880.0)) * Gain(0.1)
val superSaw = (osc1 + osc2 + osc3) / 3.0

ADSR

キーボードなどの入力装置がある場合は、ADSRエンベロープで音量に時間的変化をかける事が多い。

パラメータ	内容
Attack Time	キーが押されてからどれだけの時間で最大音量に達するか
Decay Time	最大音量に達してから、どれだけの時間で持続音量に達するか
Sustain Level	持続音量。キーが押されている間の音量。
Release Time	キーが離されてから、どれだけの時間で無音量になるか

キーが押されたら電圧が発生する波形を想定し、波形を受け取ってADSRの波形を返すクラスを作ってみる。めちゃくちゃ状態持っててIF文多いので、ちっともScalaっぽくない。もっと、良い実装ができそう。。。

class ADSREnvelope(attack:Time,decay:Time,sustain:Amplitude,release:Time)(implicit context:PCMContext)
  extends Processor {

  var decaying = false //減衰中かどうか

  def apply(waveform:Waveform):Waveform = (time:Time) => {
    val signal = waveform(time)
    if (signal > 0.0){
      if (attackTime > 0.0) {
        if (time < attackTime + attack && !decaying) {
          //Attack
          level = level + 1.0 / attack / context.sampleRate
          if (level > 1.0) {
            level = 1.0
            decaying = true
          }
        } else {
          if (time < attackTime + attack + decay || decaying) {
            //Decay
            level = level - (1.0 - sustain) / decay / context.sampleRate
            if (level 0.0) level = 0.0

          } else {
            //Sustain
            level = sustain
          }
        }
      } else {
        attackTime = time
        decaying = false
    } else {
      //Release
      attackTime = 0.0
      level = level - sustain / release / context.sampleRate
      if (level < 0.0) level = 0.0
    }
    level 
  }
}

val adsr = new ADSREnvelope(0.1, 0.2, 0.5, 0.5)
val wave = adsr(SineOsc(Freq(1.0))

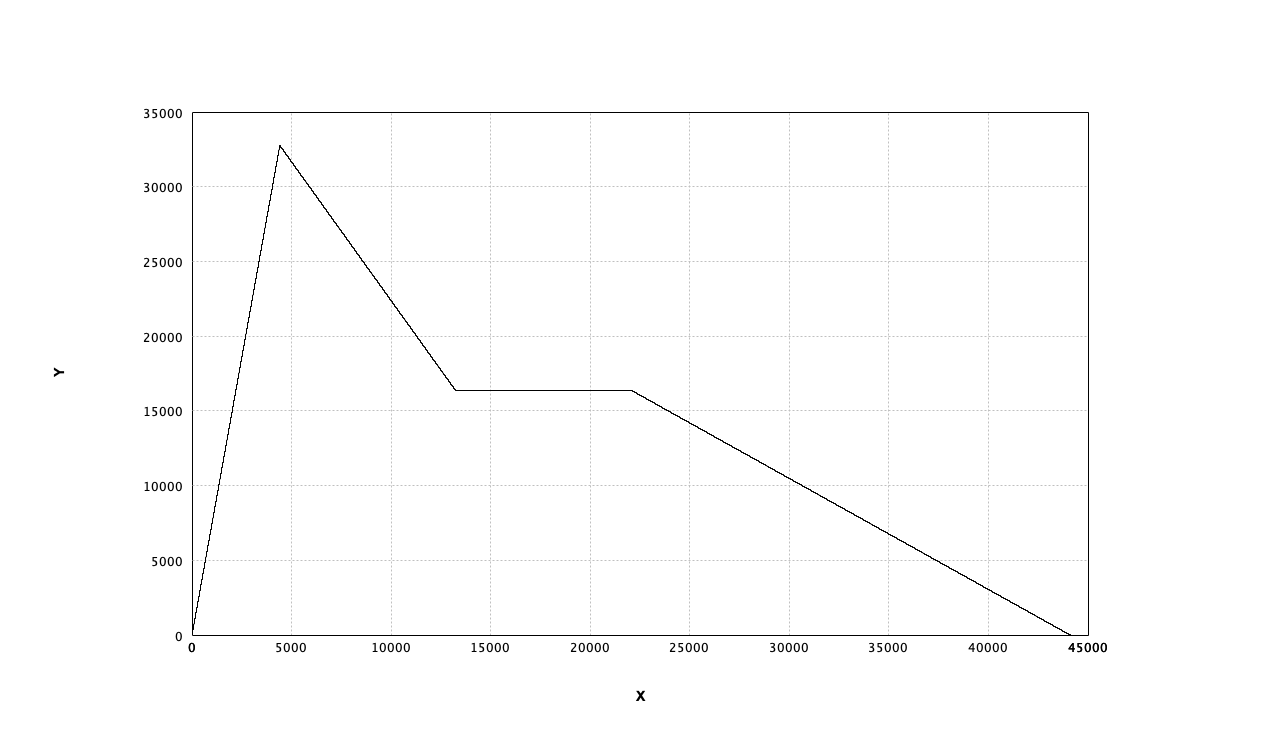
ノコギリ波の音量にADSRをかける

// 3つのオシレータを重ねた波形
val osc = (SawOsc(Freq(110.0)) + SawOsc(Freq(220.0)) + SawOsc(Freq(440.0))) / 3.0
// カットオフ周波数800、レゾンナンス1.0のフィルター
val lpf = new LoPassFilter(Freq(800.0),Gain(1.0))

//ADSRで時間的変化波形を作る(A=0.1秒,D=0.2秒,S=0.5倍,R=0.5秒）
val adsr = new ADSREnvelope(0.1, 0.2, 0.5, 0.5)

//オシレータにLPFをかけ、波形の大きさにADSRで時間的変化つけ、最終的な音量調整を行う
val wave = lpf(osc) * adsr(SineOsc(Freq(1.0)) * Gain(0.5)

折り返し雑音

サイン波は倍音を含まないので問題ないのだが、上で実装したノコギリ波には実際には問題がある。

val SawWave:Waveform = (time:Time) => (time * 2.0) % 2.0 - 1.0

サンプルレートが44.1KHzの場合、そのナイキスト周波数である22.05KHz以上の倍音がある場合は、サンプリングをうまく再生できず、低い倍音が現れてしまう（雑音が発生）。これをエイリアスノイズや折り返し雑音などと呼ぶ。

理論上はノコギリ波は無限の倍音を含むのだが、人間の耳の可聴域は20KHz程度なので、ナイキスト周波数以上の倍音は普通聞こえず、不要になる。
なので、サイン波を合成してノコギリ波を作ってみた・・・。

def SawOsc2(freq:Waveform)(implicit context:PCMContext):Waveform =
  (time:Time) => {
    val f = freq(time)
    val N = (context.sampleRate / 2 / f).toInt
    (1 to N) //1からN倍音まで
      .map(n => 2.0 / Math.PI * Math.sin(2 * Math.PI * time * f * n) / n)
      .sum
}

が、周波数が低くなると計算回数が増えるので、非常に効率が悪い。改善が必要。
n倍音のnが大きくなると振れ幅は1/nになるので、あまりに小さい振れ幅になれば足切りしても問題ないと思われる。
440Hzのノコギリ波で、N = 44,100 / 2 / 440 ≒ 50倍音まで合成した場合と、30倍音まで合成した場合では私のへっぽこ耳と、へっぽこイヤホンでは区別がつかなかった。（再生環境にもよると思うが）

周波数特性を確認する

あまり数学的なことは分かりませんが、あらゆる波がサイン波の合成でできているので、波をサイン波に分解して、どんな周波数のサイン波がどれくらい含まれているを、グラフで確認してみる。

高速フーリエ変換

FFT自前で実装しようかと思いましたが、難しいそうだったのでApache Commons Mathに含まれるFastFourieTransformerを利用します。

import org.apache.commons.math3.complex.Complex
import org.apache.commons.math3.transform._

class PCMContext extends Processor{
  // (中略)
  def fft(waveform:Waveform):Array[Array[Double]] = {
    val transformer = new FastFourierTransformer(DftNormalization.STANDARD)
    val samples = 1024
    //1024サンプル分でFFTする
    val buff = (0 until samples)
      .map(t => form(t.toDouble / this.sampleRate)
      .toArray

    transformer
      .transform(buff,TransformType.FOWARD) //FFTかける
      .slice(0, samples / 2) //ナイキスト周波数分のみ
      .map(_.abs) //複素数の絶対値
      .zipWithIndex
      .map(x => Array(n._2 / samples.toDouble * this.sampleRate, n._1)) //「周波数」「音圧」に２次元配列にする
  }

ホワイトノイズのオシレータも作っておく

class WhiteNoise extends Waveform{
  val generator = new Random()
  def apply(time:Time): Amplitude = {
    val noise = generator.nextGaussian()
    if (noise > 1.0) 1.0 else (if (noise < -1.0) -1.0 else noise)
  }
}

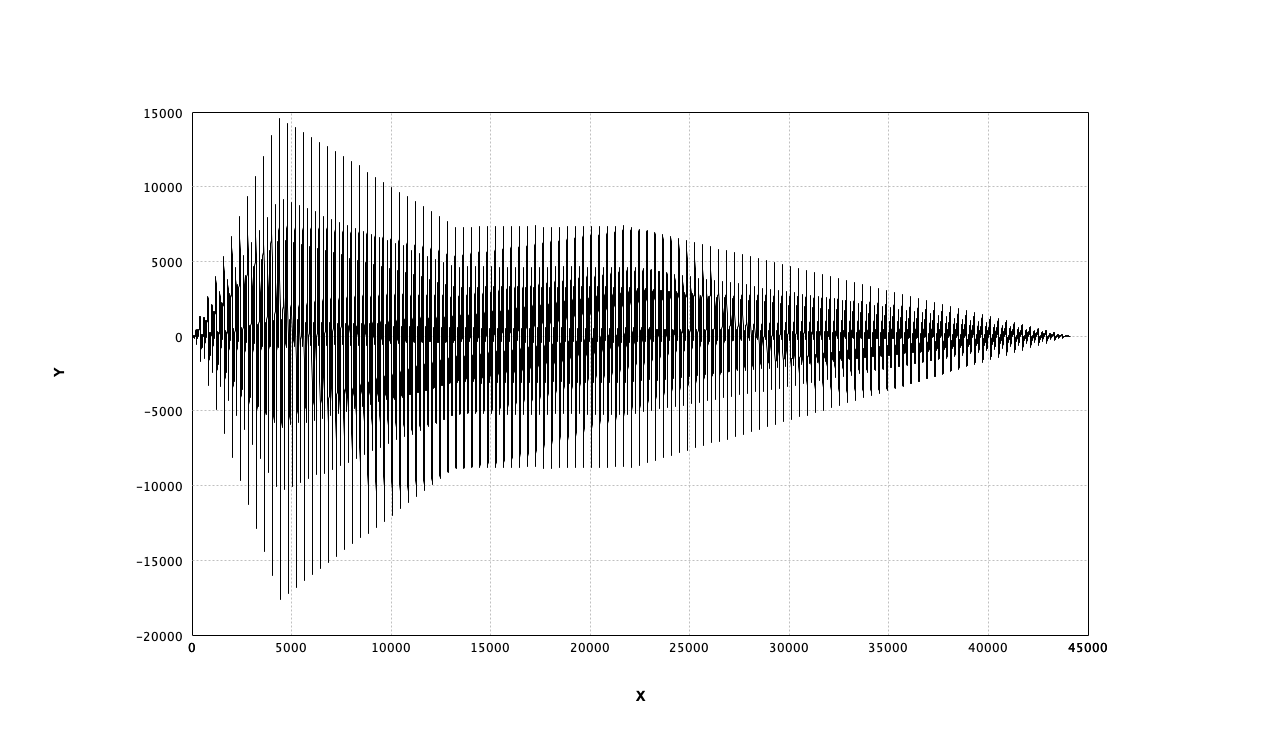
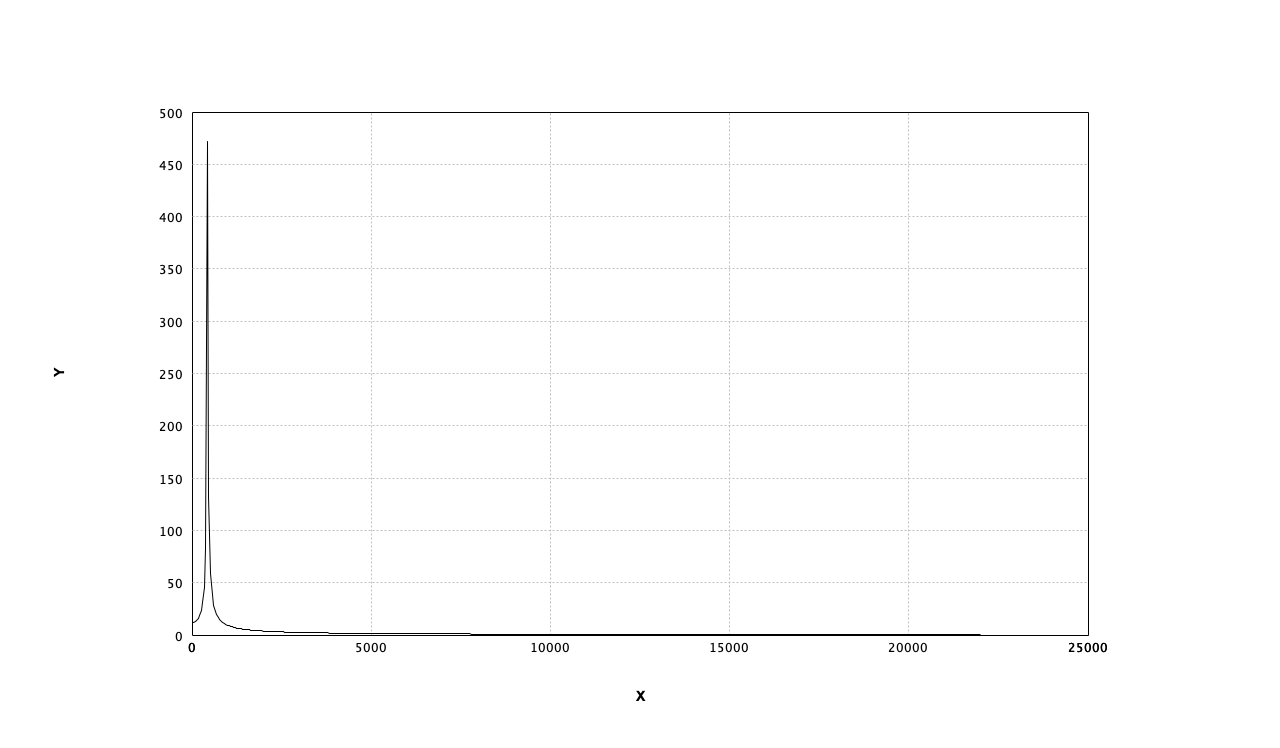
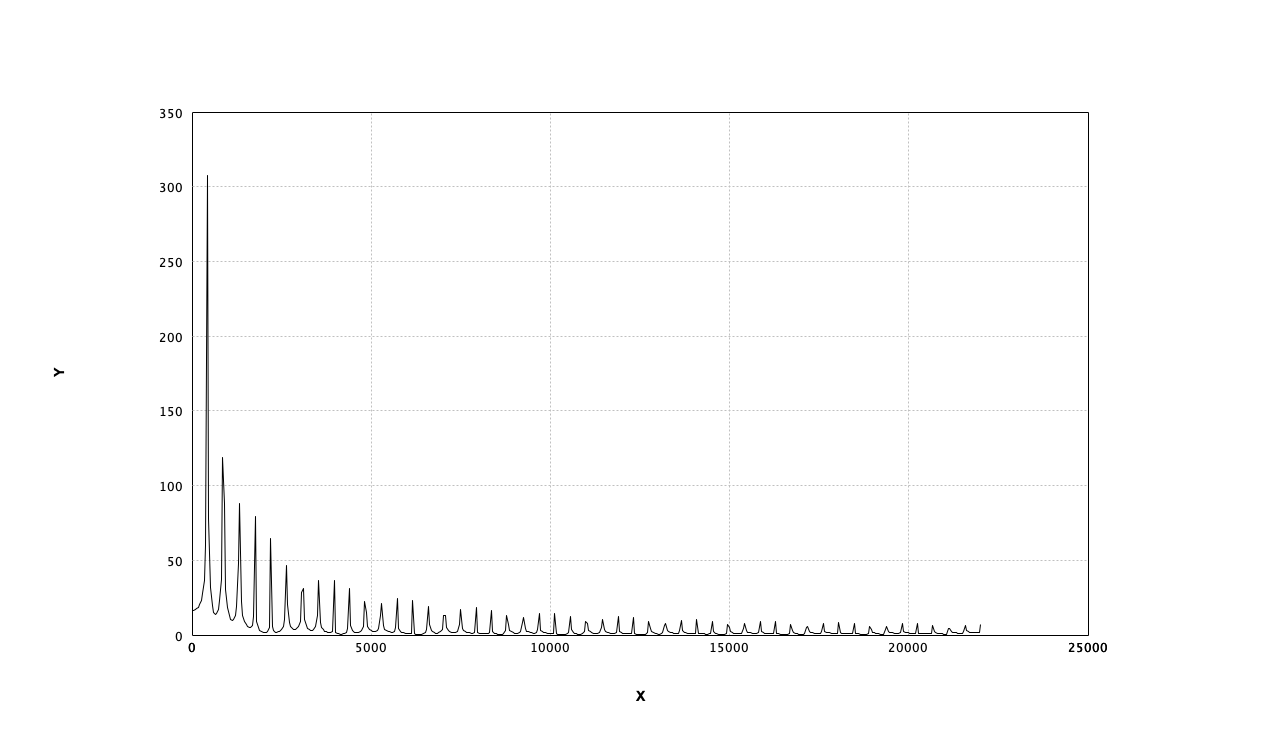
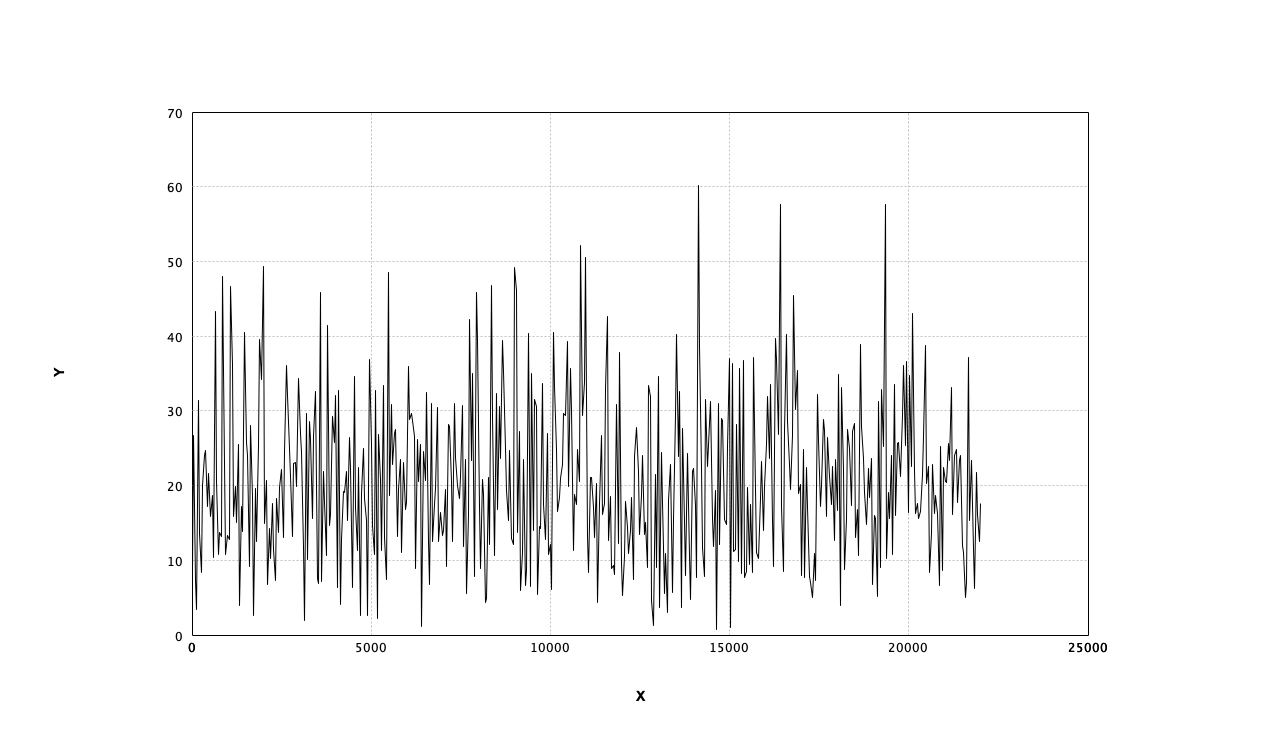
サイン波、ノコギリ波、ホワイトノイズの周波数特性を確認

440zサイン波

440Hz付近のみピークがある。

440Hzノコギリ波

440Hzから定数倍に倍音が含まれ、徐々に小さくなる。

ホワイトノイズ

ランダムに倍音が含まれている。

まとめると

これまでの実装でこんな形でシンセサイザーをプログラムできる。

//LFO
val pitchLFO = SineOsc(Freq(1.0)) * 2.0

//オシレーター
val osc = (SawOsc2(Freq(440.0)  + pitchLFO) +
           SawOsc2(Freq(218.0)  + pitchLFO) +
           SawOsc2(Freq(881.0)  + pitchLFO)) / 3.0

//フィルター
val filter = new LoPassFilter(Freq(1000.0),Gain(1.0))

//ADSR
val adsr = new ADSREnvelop(0.1,0.1,0.8,0.5)
val keyon = SineOsc(Freq(1.0))

//結線
val output = adsr(keyon) * filter(osc) * Gain(0.5)

//２秒間再生
output.play(2.0)

//フーリエ変換
output.fft()

最後に

サウンドプログラミングは初めてだったが、あらゆる信号を波形型(Waveform)とし、全てのパラメータを波形型で統一することで、LFOやADSRといった変調を簡単に実装できるのが面白い発見でした。