量子アニーリングを用いたEVシェアの最適化：量子アニーリングソリューションコンテストより

はじめに

Everybodyこんにちは． 深水と言います．
この記事では，みなさんご存知の大関先生や東北大学が主催となって開催した，量子アニーリングソリューションコンテストで発表した内容について紹介させてもらいます．下のwebサイトに行けば，コンテストの概要や，全ての発表動画を見ることができます． (ちなみにまだ結果は出てませんが，優勝者はカナダのD-Wave本社まで連れて行ってくれるそうです．ファンタスティック!!)

私たちは，チーム名：QuantumPredator ，発表タイトル： EVerify として発表しました．
内容は 量子アニーリングを用いたEVシェアの最適化 についてです．

EVerifyの発表動画リンク↓

チームメンバーは東北大学情報科学研究科 小林・佐藤研究室の以下３名で，この記事も共同執筆です．
東北大学情報科学研究科　博士後期課程1年　熊谷政仁​
東北大学工学部機械知能航空工学科　4年　深水一聖​
東北大学工学部機械知能航空工学科　3年　小野田誠

記事後半では発表では説明しきれなかった，詳しいQUBOの説明もしたいと思います．
かなり面白いテーマを，Domain Wall Encodingなどの最新技術で取り組んでいるので，読んでいただいているみなさんに何かいい気づきなどを与えることができれば嬉しいです．
では発表内容について紹介させてもらいます！

背景

環境保護のためCO2の削減

CO2削減目標が定められ，世界的に取り組まなければいけない課題となっています．

• パリ協定:気温上昇を2℃未満に,努力目標として1.5℃未満に抑える
• COP26:努力目標だった1.5℃が明確な目標に

また，先進国では2050年のカーボンニュートラル,2030年までの地球温暖化ガス排出量50%の削減が目標になっています．

EVの世界的な普及・ガソリン車の廃止

2035年までに,世界的にガソリン車がEVに刷新される見通しであり，各国で政策レベルの議論が行われています．

• EU
  • 2035年までに,世界的にガソリン新車販売の禁止
  • ハイブリッド車も禁止
• 中国
  • 主要法規2021年にNEV規制が改訂
  • 2035年をめどに新車をすべて環境対応車
• アメリカ
  • カリフォルニア州で2035年までに州内の新車で内燃機関の廃
  • バイデン大統領が2030年までに国内販売車の新車40~50%電動化する大統領令を発令
• 日本
  • 2035年までに軽を含めて新車100%電動化方針を発表 ## EVシェアの拡大 一方で，EVには次の2つの課題から，シェアを前提とした普及が叫ばれています．
• EVのバッテリーに使用するレアメタルの偏在や将来的な枯渇
  • 台数の確保が難しい
    • ガソリン車の4倍以上のレアメタルが必要
  • 価格が高くなりやすい
    • 300万を超える車体価格:補助金を含めてもガソリン車より高価
• シェアを前提としたEVの普及
  • 安価な値段で提供
  • 生産台数を抑え,消費資源や製造時のCO2削減 ## 提供ソリューション 私たちは，東北大学主催の量子アニーリングソリューションコンテストにエントリーし，量子アニーリングを活用したEVシェアサービスとして，「EVerify ~EVeryone EVeryday EVerywhere~」に取り組みました．

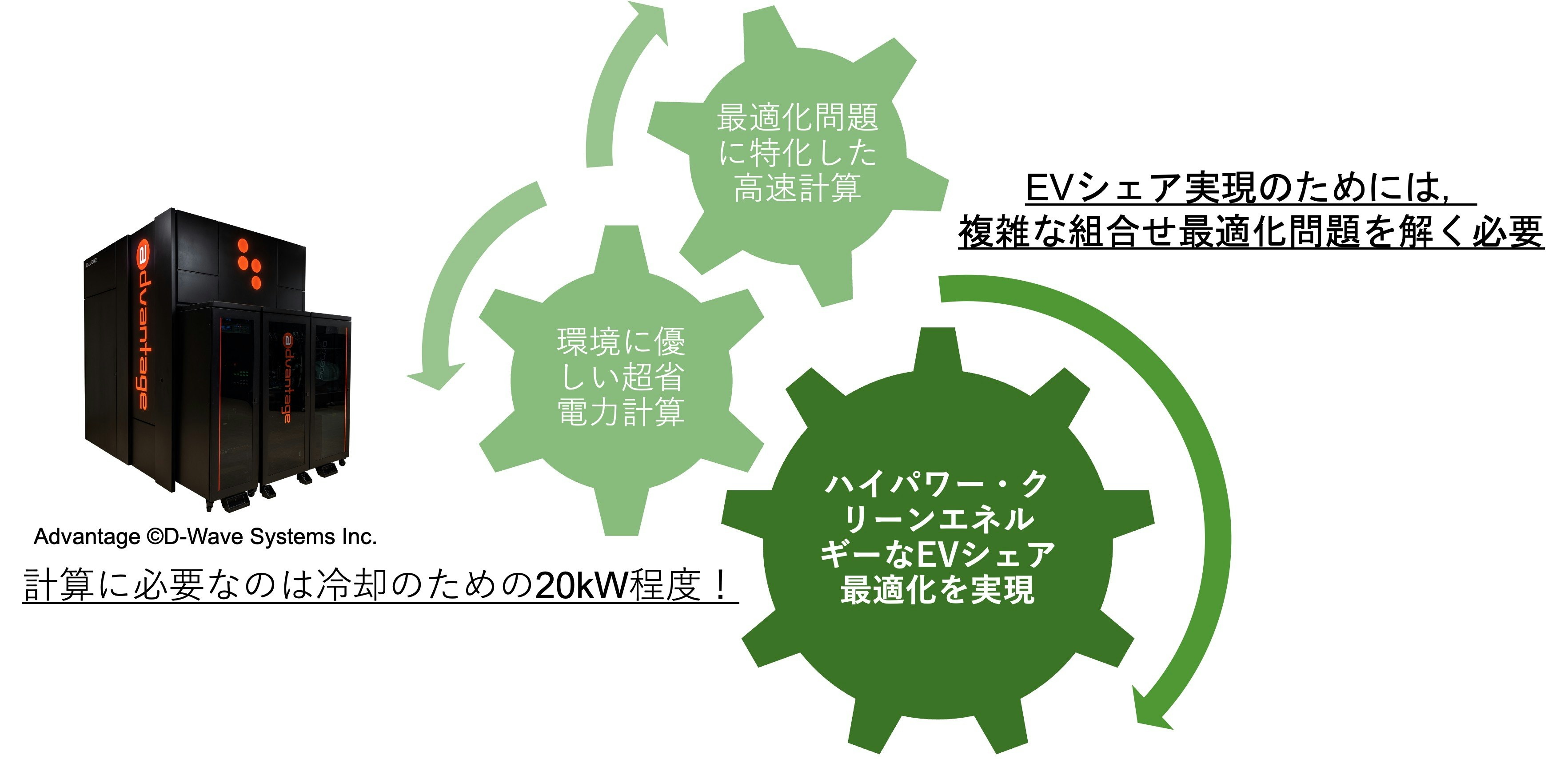
量子アニーリング×EVシェア

EVシェア実現のためには複雑な組み合わせ最適化問題を解く必要がありますが，量子アニーリングなら，最適化問題に特化した高速計算が期待できます．また，計算には冷却のためのごく僅かな電力しか使用しないので，環境にも優しい超省電力計算が期待できます．
量子アニーリングとEVシェアの組み合わせは，ハイパワー・クリーンエネルギーな最適化を実現に適していると考えています．

解決すべき課題

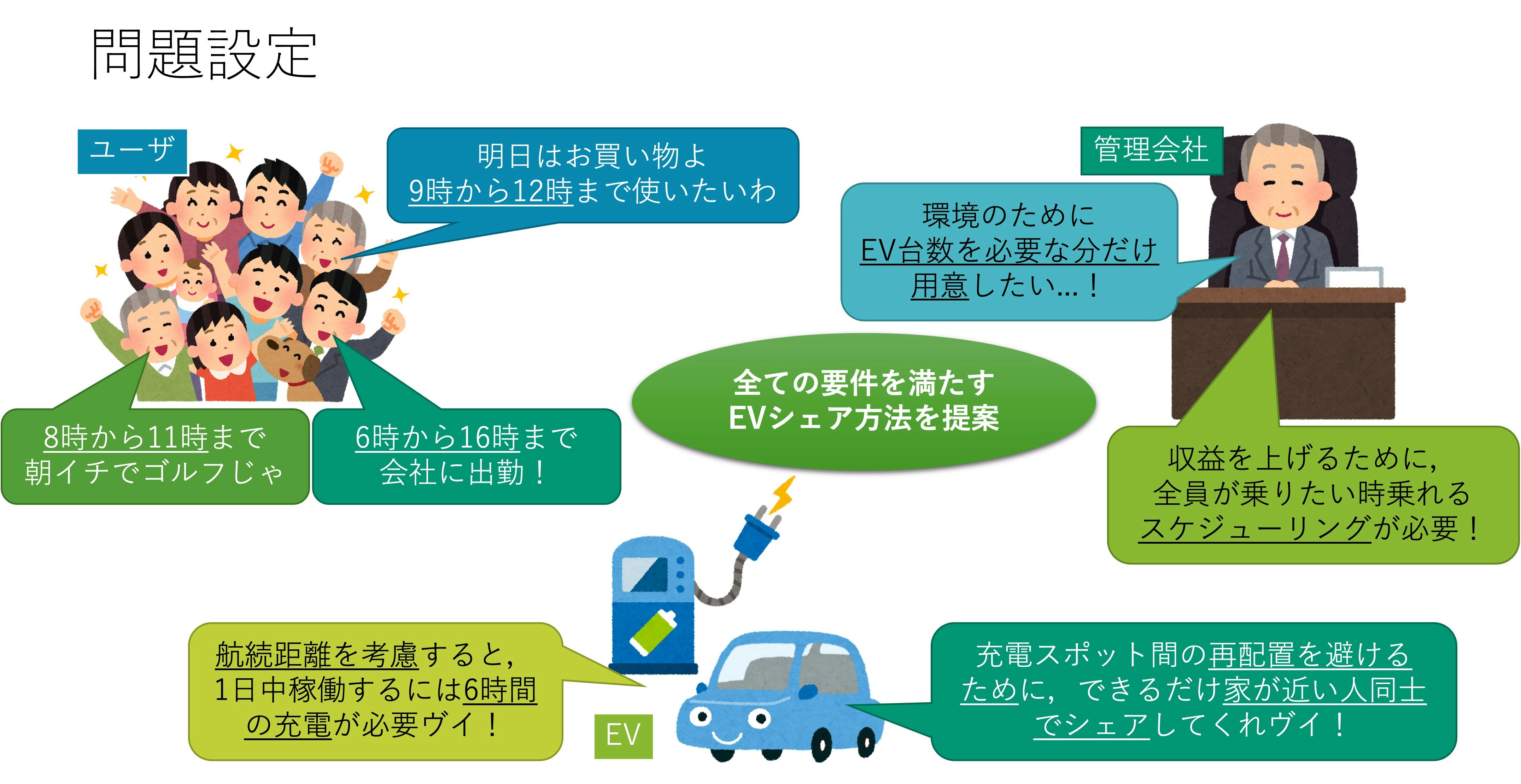
住民目線の課題

管理会社目線の課題

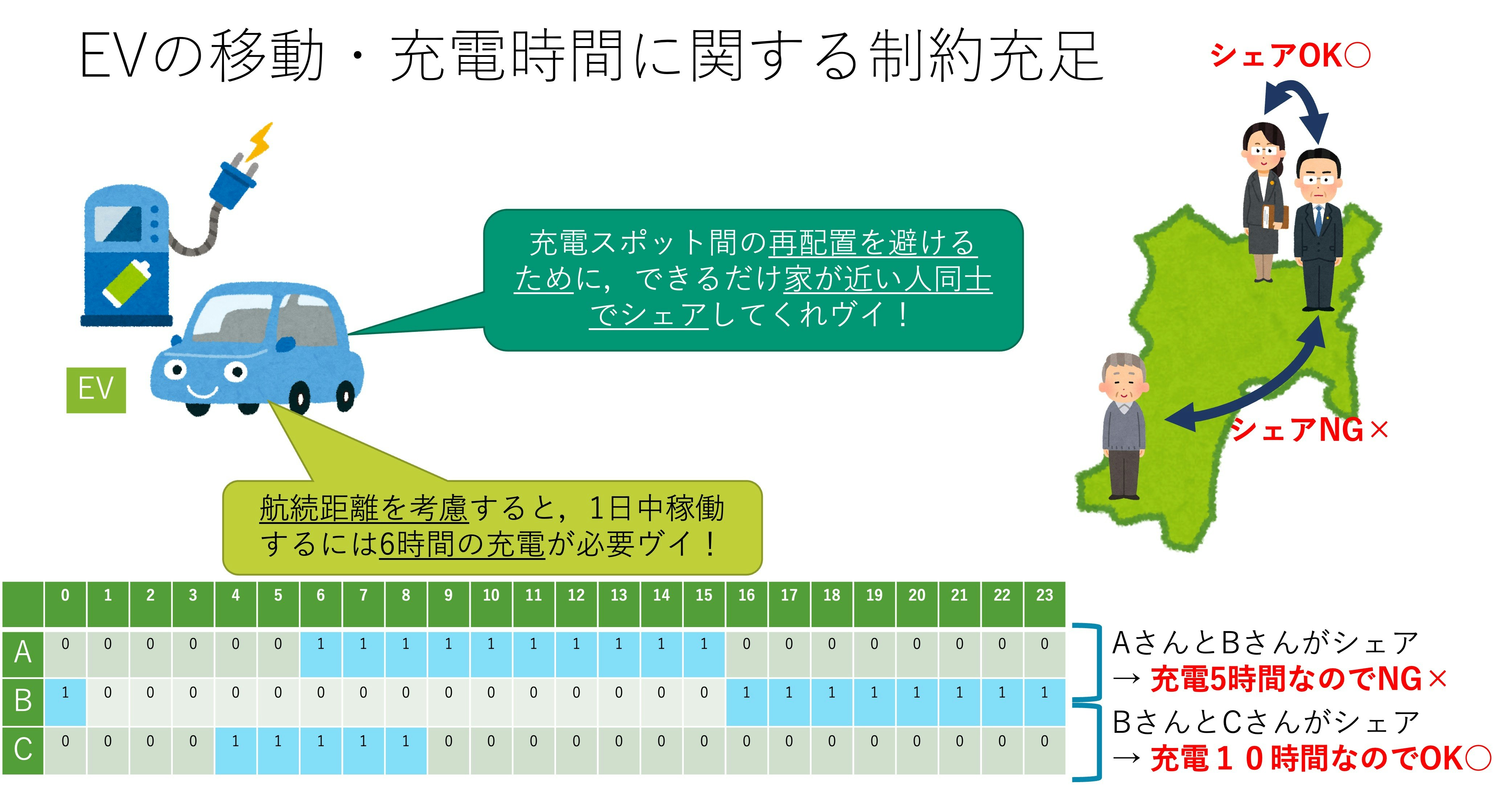
EV目線の課題

最適化の全体像

最適化は，このワークフローの反復計算によって行われます．

• ユーザ：前日に，明日EVを利用したい時間を設定することで，競合が起きないようどのEVを使うべきか提案されます．
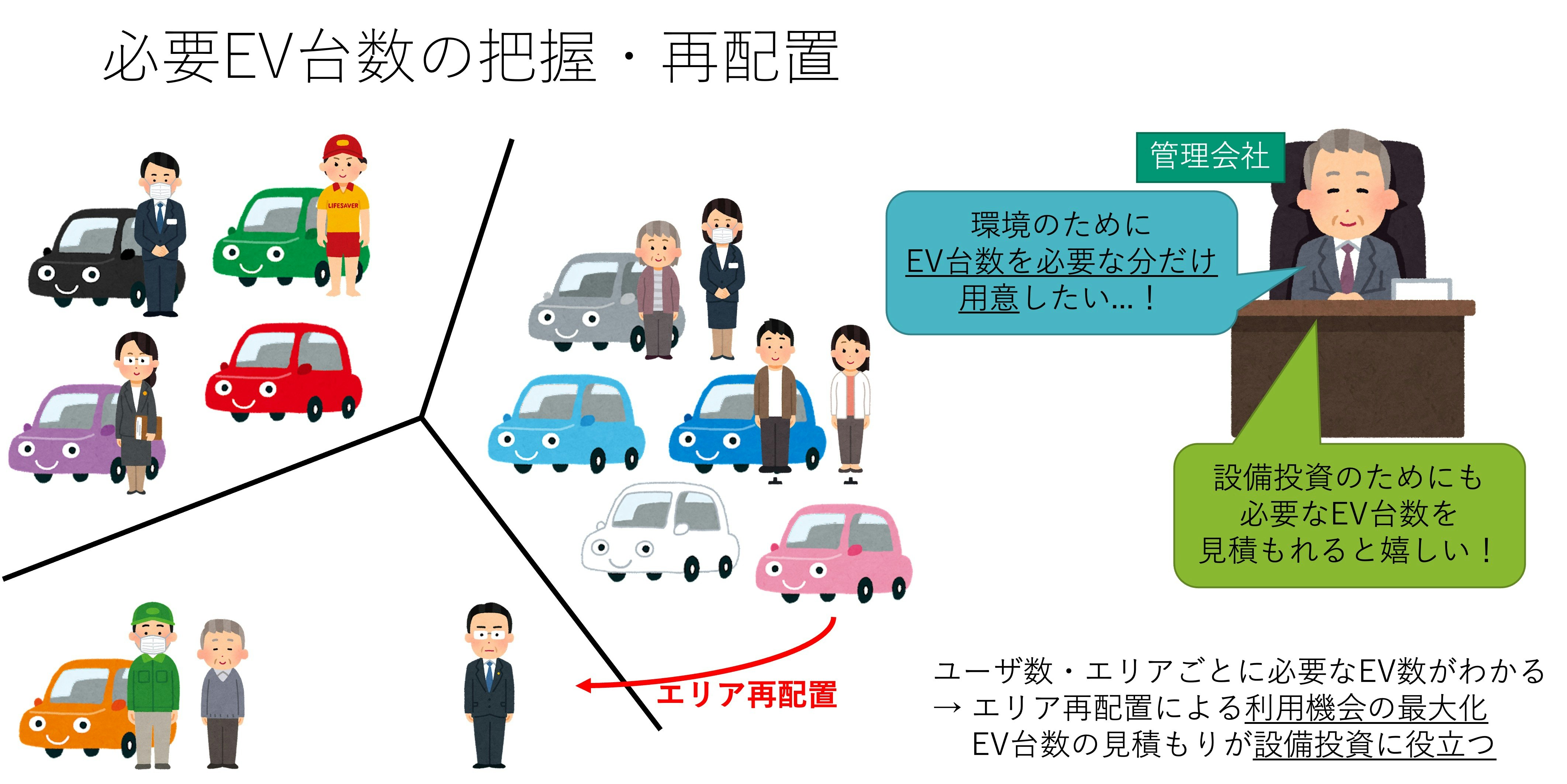
• 管理会社：ユーザ全体のスケジュール情報や，ユーザの居住地充電エリアを考慮して，明日どの充電エリアに何台のEVを配置しておけば良いか求めることができます．EVの必要台数を求めることは，設備投資にも役立ちます．

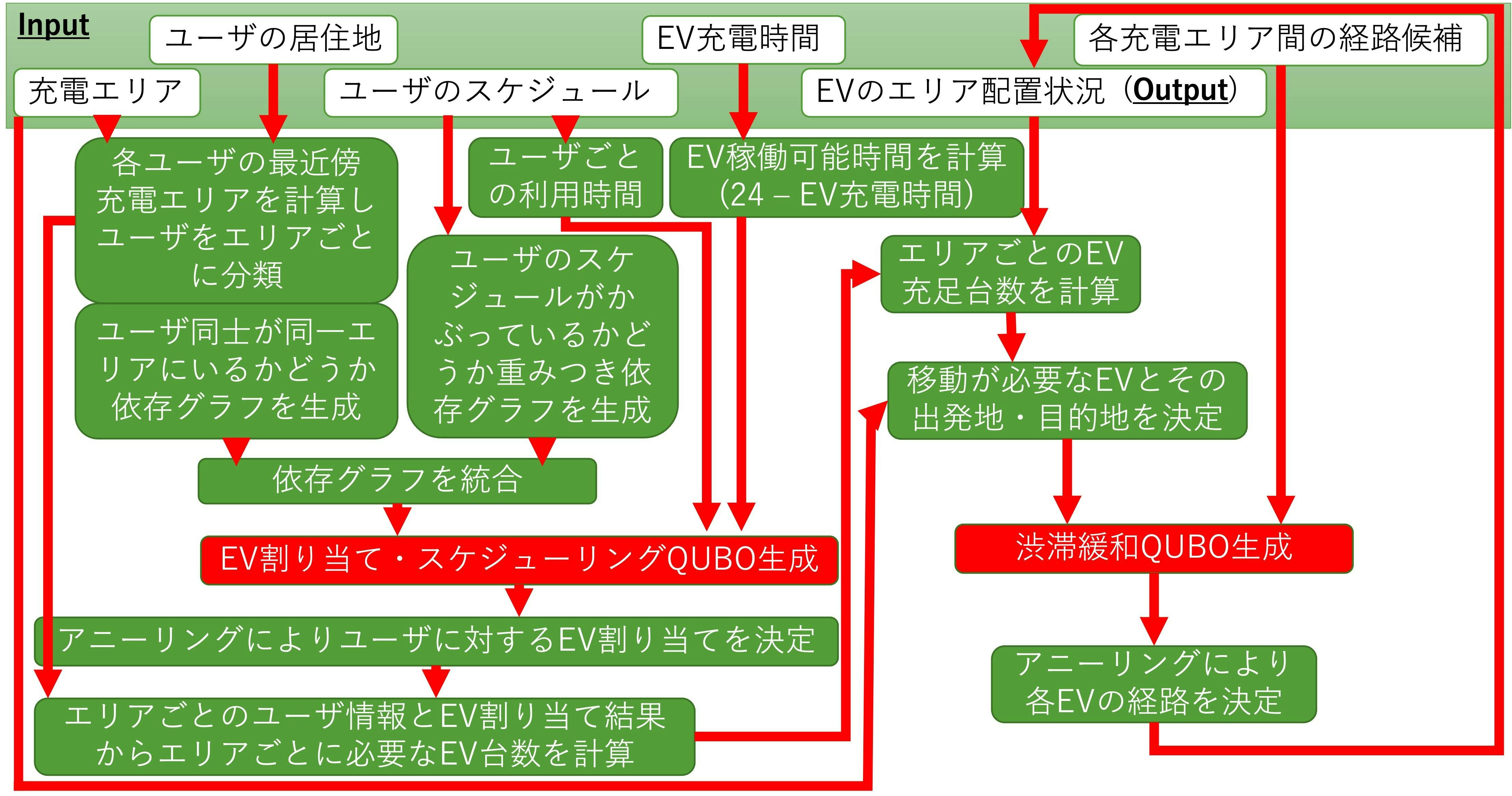
QUBO化については，次の流れで進めます．
1. One Hot Encodingで定式化
2. One Hot Constraint部分を Domain Wall Constraintに変換
3. Domain Wall Constraint以外の部分のOne Hot Encodingで書かれた式をOne Hot Encodingに変換

One Hot Encoding ではなく，Domain Wall Encodingで最適式化をする理由は，One Hot Constraint部分のビット間相互作用を減らすためです．結合数の多いOne Hot Constraintはしばしば最適化の精度を低下させます．

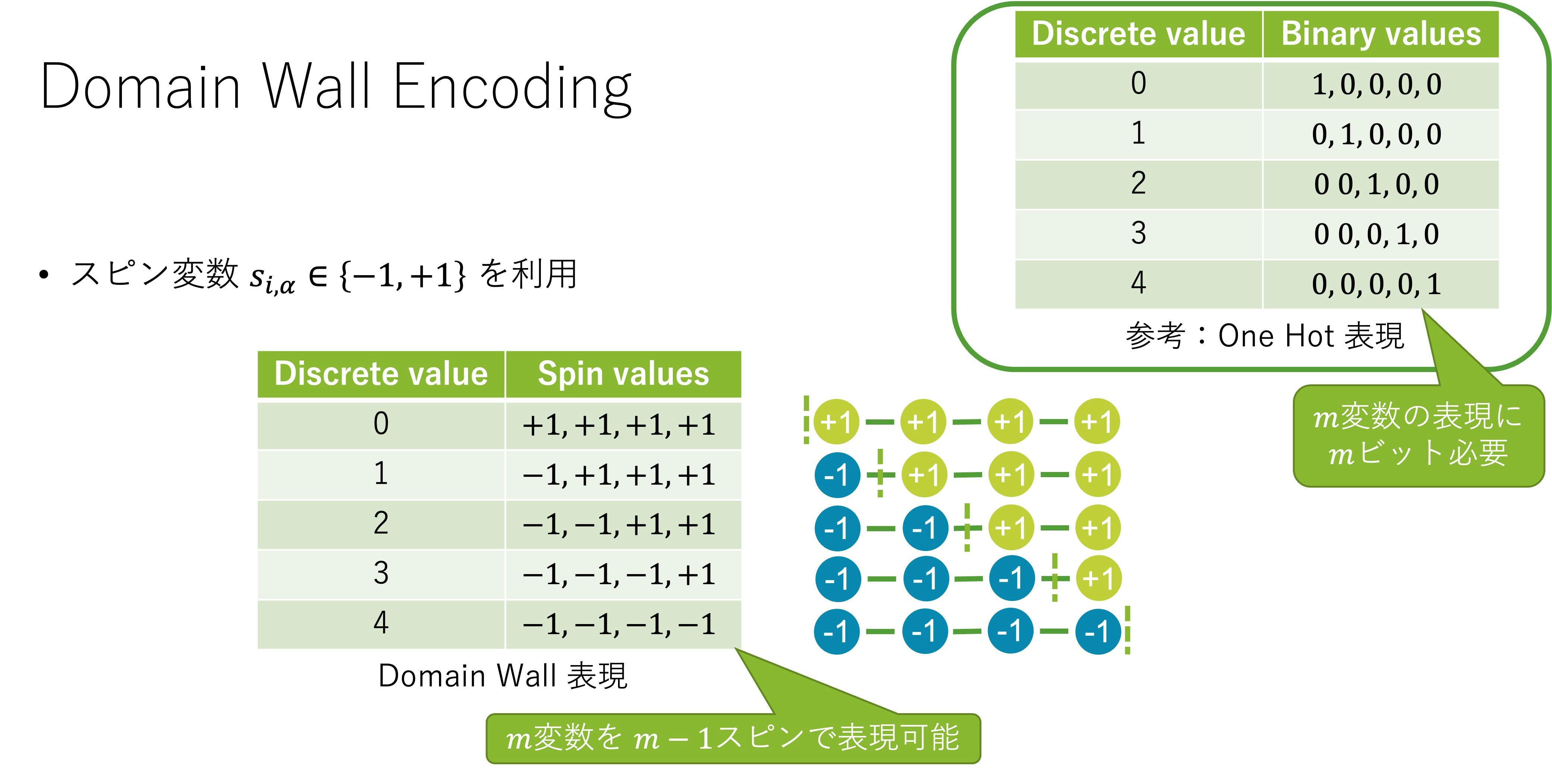
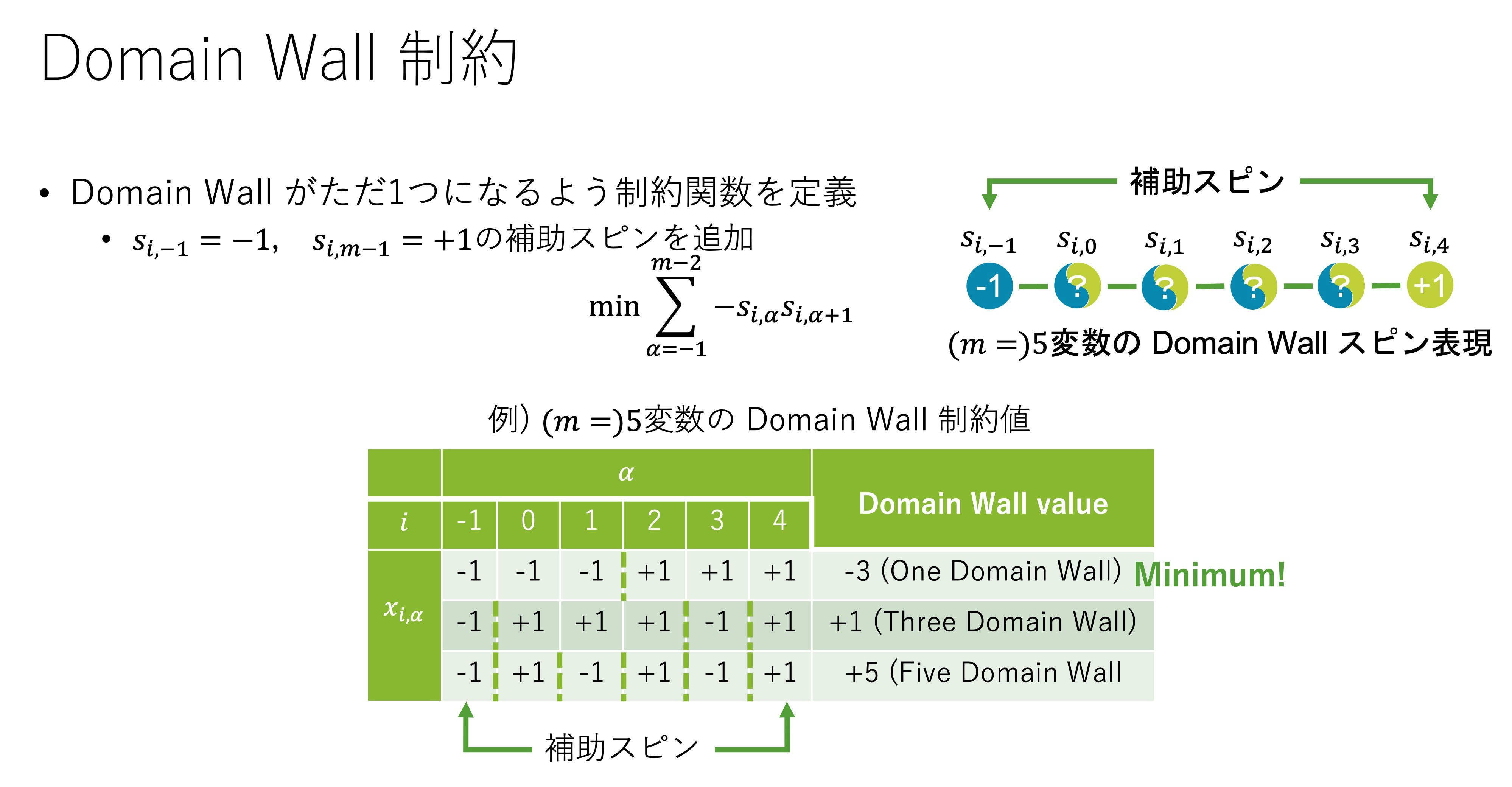
Domain Wall Encoding [Chancellor, 2019]

• EVシェア最適化には多くの制約が必要
  • 道路状況の他に,充電時間や航続距離を考慮
    • 量子ビット間の相互作用が多くなる見込み
    • 量子アニーリングの精度が低下する可能性
  • Domain Wall Encodingによる離散変数表現
    • 従来広く用いられるOne Hot Encodingより少ない量子ビット数と相互作用数

Performance	One Hot Encoding	Domain Wall Encoding
量子ビット数/スピン数	$$m$$	$$m-1$$
相互作用数	$$\frac{1}{2}m(m-1) $$	$$m-2$$
グラフ構造	完全グラフ	線形グラフ

Domain Wall Encodingにより,少ない量子ビット数と相互作用数で多制約最適化を実現できる可能性があります．

EV割当・スケジューリング最適化

変数

まずは，One Hot Encodingによる定式化を行います．

• ユーザ$i$がEV$\alpha$を使用する$x_{i,\alpha}=1$
• ユーザ$i$がEV$\alpha$を使用しない$x_{i,\alpha}=0$

最適化に必要な要素

• 各ユーザのEV利用時間 $L_i$
• EV稼働可能時間 $T_{act}$
• 依存グラフ $E$ (あとで説明)

最適化の方針：EV利用時間Tαの均等化

いま，$T_{\alpha}=\sum_{\alpha}^{N−1} L_i x_{i, \alpha}$と EVの利用時間$T_{\alpha}$を定義します．

すると，EV利用時間の均等化は，次式によって行われます．
$
min \sum_0^{N−1}L_i x_{i, 0} \
s.t.⁡T_{\alpha}　\leq　T_{0}
$

EV稼働可能時間 (充電時間)に関する制約は，次式で与えられます．
$
T_0 \leq T_{act}
$

Log Encodingによる不等式制約のQUBO化

全てのEVの利用時間$T_{\alpha}$が$T_0$を超えない

$$
T_{\alpha} \leq T_0
$$

$\overline{\Delta T(0,\alpha)}$を$T_{0}$と$T_{\alpha}$の差の上限とする

$$\therefore T_0−T_{\alpha}=\sum\limits_{i=0}^{N−1}L_i (x_{i,0}−x_{i,\alpha} ) \leq \overline{\Delta T(0,\alpha)} \because T_{\alpha}=\sum\limits_{0}^{N−1}L_i x_{i, \alpha} $$

Log Encoding により，

$0 \leq \sum_{i=0}^{{\lfloor\log_2 (\overline{\Delta T(0,\alpha)}-1 )\rfloor }}2^i𝑦_i \leq \overline{\Delta T(0,\alpha)}(𝑦_i\in{0, 1})$

を考える

$$
\overline{\Delta T(0,\alpha)} = \sum\limits_{i=0}^{\lfloor\log_2 (\overline{\Delta T(0,\alpha)}-1 )\rfloor }2^i y_i +\sum\limits_{i=0}^{N−1}L_i(x_{i, 0}−x_{i, \alpha})
$$

等式制約なので，次の制約関数が得られる

$$
\min \Bigl{⁡\sum_{\alpha=1}^{M−1}{\Delta T(0,\alpha)−\sum_{i=0}^{N−1}L_i (x_{i, 0}−x_{i, \alpha} )−\sum_{i=0}^{\lfloor\log_2 (\overline{\Delta T(0,\alpha)}-1 )\rfloor }2^i y_i}\Bigr}^2
$$

$T_0$がEV稼働可能時間$T_{act}$を超えない$T_0　\leq T_{act}$についても，Log Encodingを用いた同様の式展開により，

$$
min\Bigl{⁡(\Delta T(act,0)−T_{act}+\sum_{i=0}^{N−1}L_ix_{i, 0}−\sum_{i=0}^{\lfloor\log_2 (\overline{\Delta T(0,\alpha)}-1 )\rfloor }2^i z_i)^2 \Bigr}
$$
ここまでで，充電時間を考慮したEV利用時間の均等化が完了しました．さらに，スケジュール・エリアの制約について考えます．

エリア・スケジュールの同時依存回避

依存グラフ$E$について，次式を考えます．
$$
min⁡\sum\limits_{\alpha=0}^{M−1}\sum_{𝑖<𝑗}E_{i,j} x_{i, \alpha} x_{j, \alpha}
$$

• エリア依存グラフ
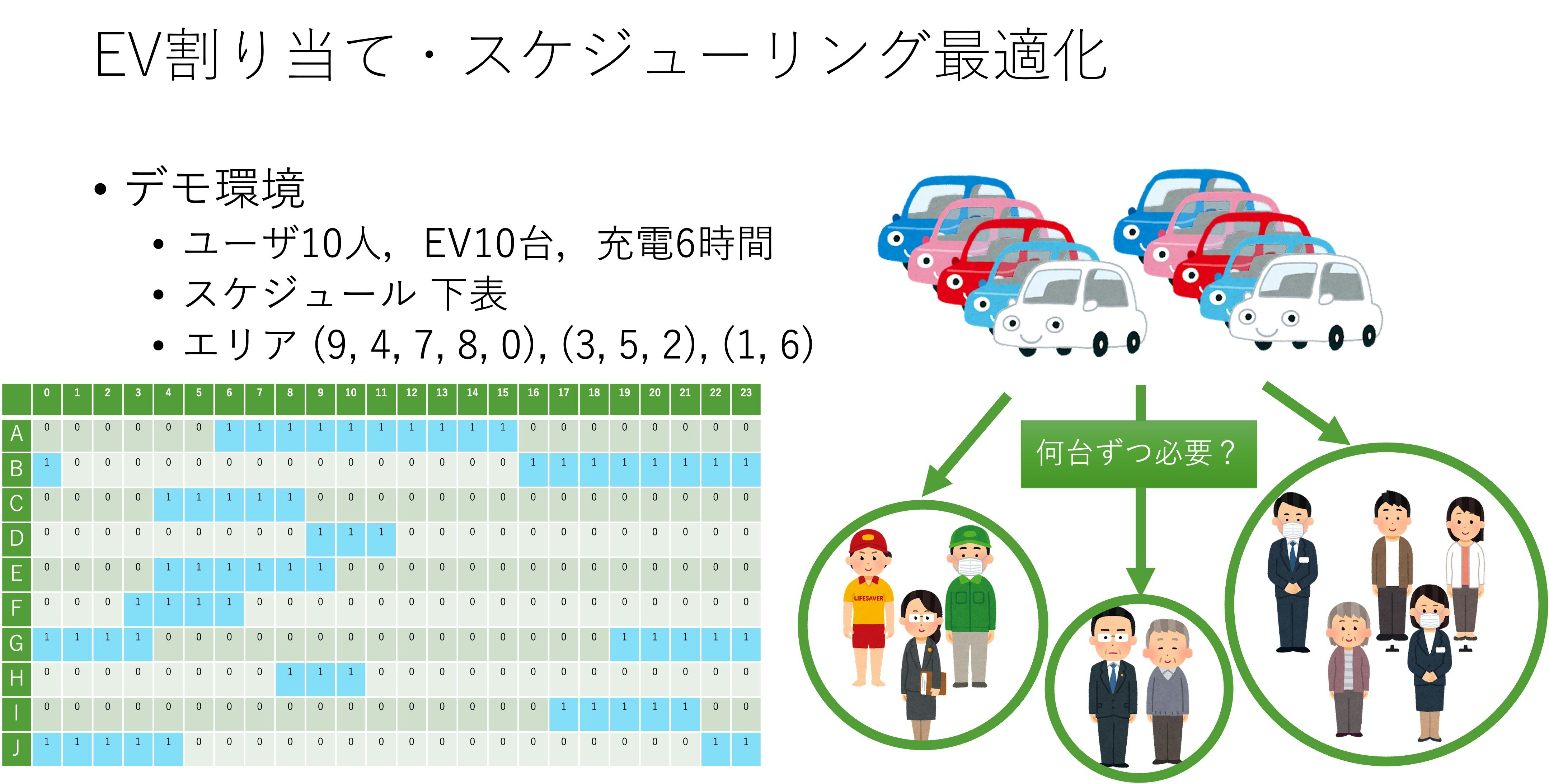
  エリアごとのユーザリスト：$U={0: (9, 4, 7, 8, 0), 1: (3, 5, 2), 2: (1, 6)}$
  行列$E_{area}$を考えて，ユーザ同士が別のエリアにいるなら1, 同じエリアなら0

• スケジュール依存グラフ
  ユーザ同士がかぶっている利用時間数を要素にもつ行列$E_{schedule}$

２つの依存グラフを時間の単位に直して統合します．
$$E=T_{act} E_{area}+E_{schedule}$$

これにより，次にような最適化が行われます．
依存グラフの要素$E_{i,j}$が大きい時，$x_{i,\alpha}$と$x_{j, \alpha}$のどちらかは0 → スケジュールがかぶっている or エリアが異なる

$E_{i,j}=0$なら$x_{i,\alpha}$と$x_{j, \alpha}$が両方1になっても問題ない → スケジュールがかぶっていない and エリアが同じ

各ユーザをただ一つのEVに割り当てる制約

普通はOne Hot Constraintを使いますが，今回はDomain Wall Constraintを使います．これは相互作用数を削減するためです．
$$
-\sum\limits_{i=0}^{N-1}\sum\limits_{\alpha=-1}^{M-2}(1-2b_{i,\alpha}-2b_{i,\alpha+1}+4b_{i,\alpha}b_{i,\alpha+1})
$$

One Hot Encoding と Domain Wall Encoding の変換

$$x_{i, \alpha}=b_{i,\alpha−1}−b_{i, \alpha}$$
で行えます．

QUBOの全体像

$$H_{objective}=\sum\limits_{0}^{N-1} L_i(b_{i,-1}-b_{i,0}) $$

$$H_{othercar}=\sum\limits_{\alpha=1}^{M-1} \Bigl{\Delta T(0,\alpha)-\sum\limits_{i=0}^{N-1}L_i(b_{i,-1}-b_{i,0}-b_{i,\alpha-1}+b_{i,\alpha})-\sum\limits_{i=0}^{\lfloor\log_2 (\overline{\Delta T(0,\alpha)}-1 )\rfloor }2^iy_i \Bigr}^2$$

$$H_{charging}= \biggl(\Delta T(act,0)-T_{act} + \sum\limits_{i=0}^{N-1}L_i(b_{i,-1}-b_{i,0}) -\sum\limits_{i=0}^{\lfloor\log_2 (\overline{\Delta T(act,0)}-1 )\rfloor }2^iz_i \biggr) ^2$$

$$ H_{dependency} = \sum\limits_{\alpha=0}^{M-1}\sum_{i<j}E_{i,j}(b_{i,\alpha-1}-b_{i,\alpha})(b_{j,\alpha-1}-b_{j,\alpha}) $$

$$ H_{domain-wall}=-\sum\limits_{i=0}^{N-1}\sum\limits_{\alpha=-1}^{M-2}(1-2b_{i,\alpha}-2b_{i,\alpha+1}+4b_{i,\alpha}b_{i,\alpha+1}) $$

$$ H_{all}=AH_{objective}+B_1H_{other-car} + B_3H_{dependecy} + \kappa H_{damain-wall} $$

$$(A=1,B_1=1,B_2=1,\kappa = 24)$$

渋滞緩和最適化 [Florian et.al., 2017]

Volks Wagenの有名な論文と同じQUBOを使います．ある車$i$に対して$k$個の経路パターンを与え$x_{i,k}$を選ぶときは$x_{i,k} = 1$、選ばないときは$x_{i,k}=0$として考えます．

コスト関数は、ある経路$(i,k)$について、道路$e$を通るかどうかを示す$C_{e, (i,k)}$を用意します．この$C_{e, (i,k)}$は$0$または$1$を持ち、道路$e$を通る場合は$C_{e, (i,k)}=1$、道路$e$を通らない場合は$C_{e, (i,k)}=0$とします．

One Hot Encoding を用いたQUBOは次にようになります．
$$ H= \sum_e \biggl( \sum\limits_{i=0}^{N-1}\sum\limits_{k=0}^{K-1}C_{e(i,k)}x_{i,k} \biggr)^2+\lambda\sum\limits_{i=0}^{N-1}\biggl( \sum\limits_{k=0}^{K-1}x_{i,k-1} \biggr)^2$$

これにDomain-Wall　Encodingを適用すると,One-Hot ConstraintがDomain-Wall Constraintになります．さらに，$x_{i,k}=b_{i,k-1}-b_{i,k}$を適用します．
$E(x) = \sum_{e} \left( \sum_{i,k} C_{e, (i,k)}(b_{i,k-1}-b_{i,k}) \right)^2 - \kappa \sum_{i=0}^{N-1} \sum_{k=-1}^{K-2} (1-2b_{i,k})(1-2b_{i,k-1})
$

仙台市泉パークタウンでのデモンストレーション

• 泉パークタウンのスマートシティ計画 (参考資料)
  • 住民目線による都市OS最適化を目指し,持続可能な街全体のアーキテクチャを構築
  • 交通・物流面では,公共交通機関の効率化とEVシェア拠点の構築
• デモンストレーション
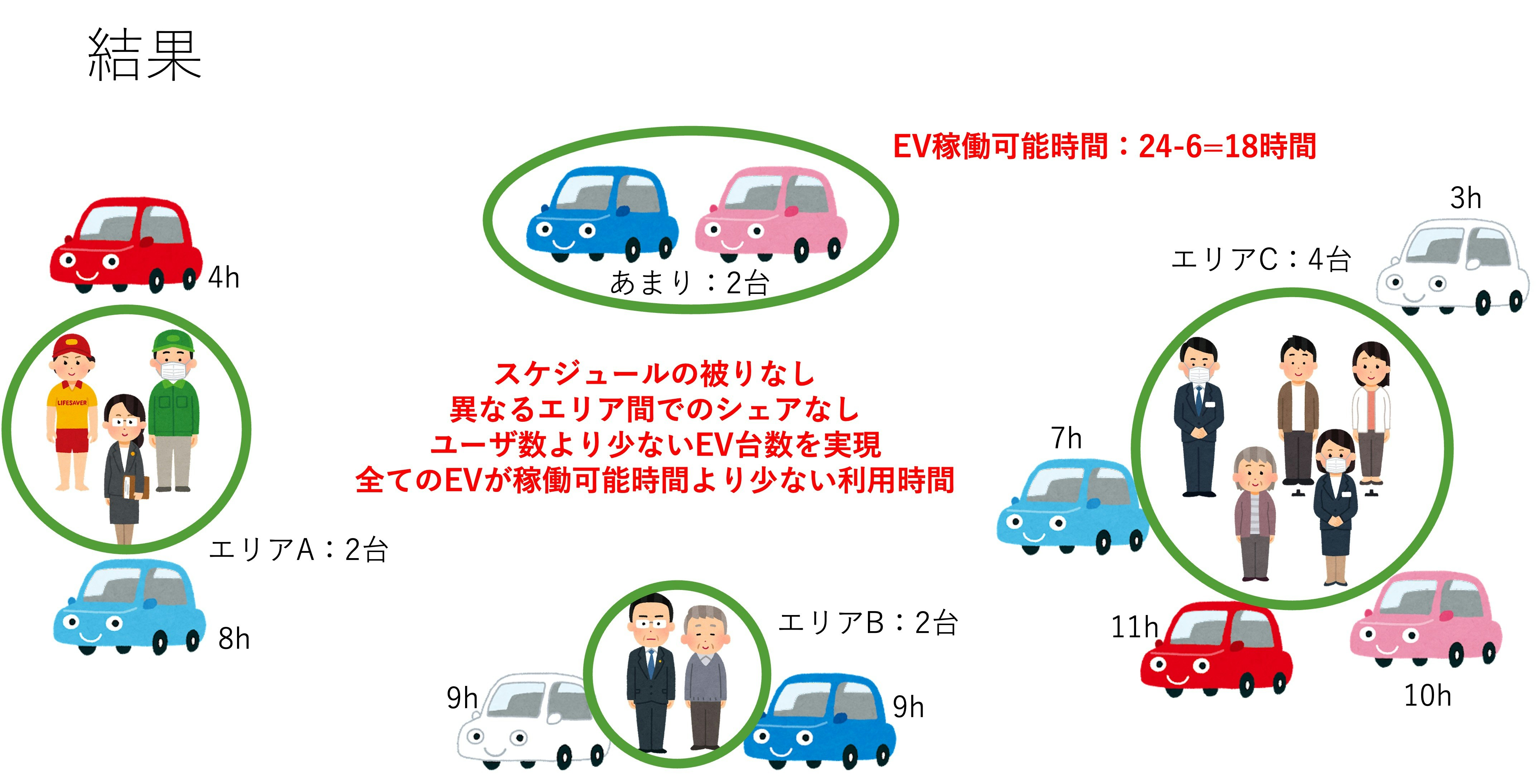
  • 泉パークタウンの住民を想定してユーザを選択し，EV割り当て・スケジューリング最適化
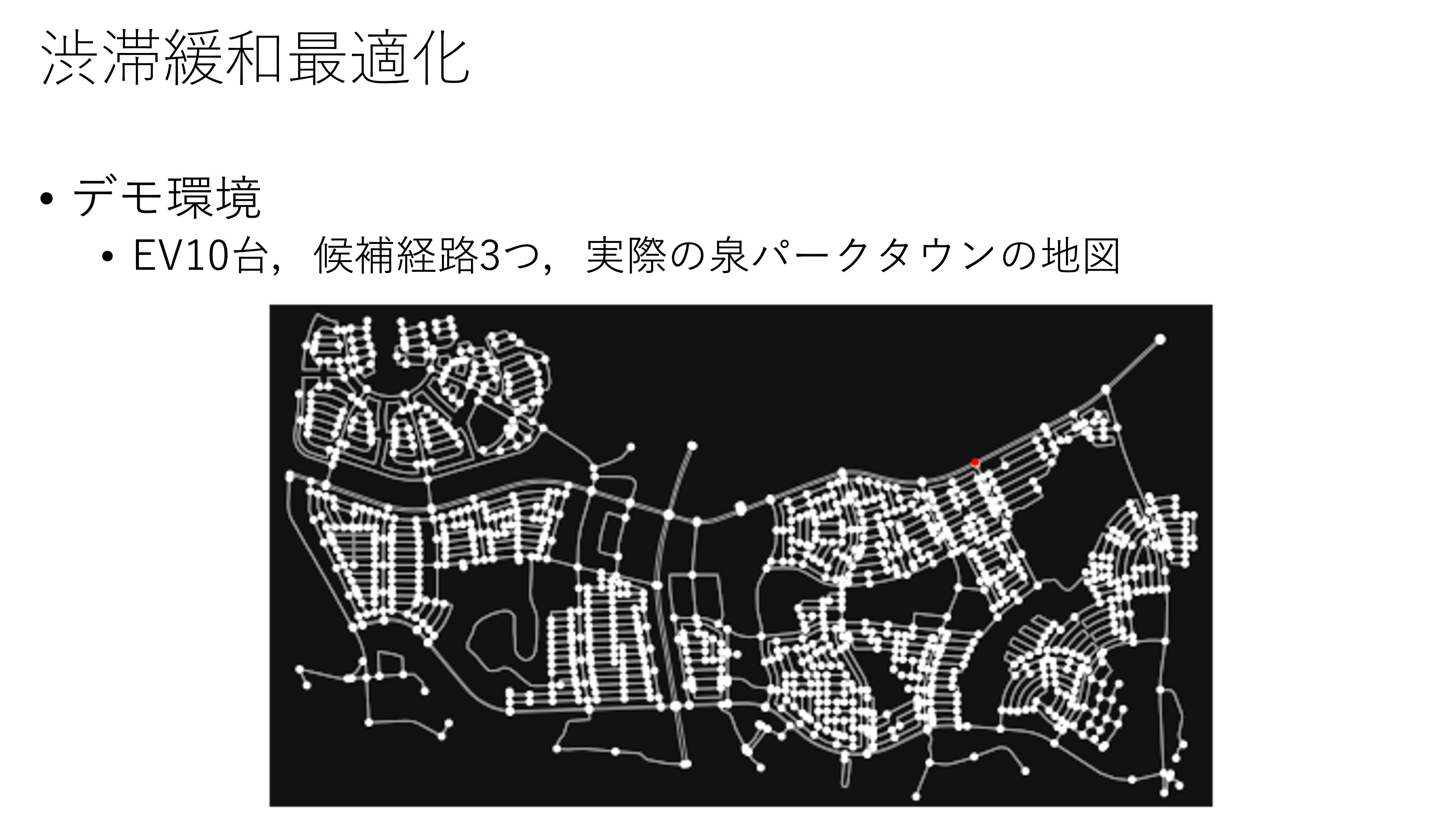
  • 実際の地図上で，渋滞緩和最適化を行い，交通量を可視化

コードはColabで公開中です．ぜひ試してみてください！

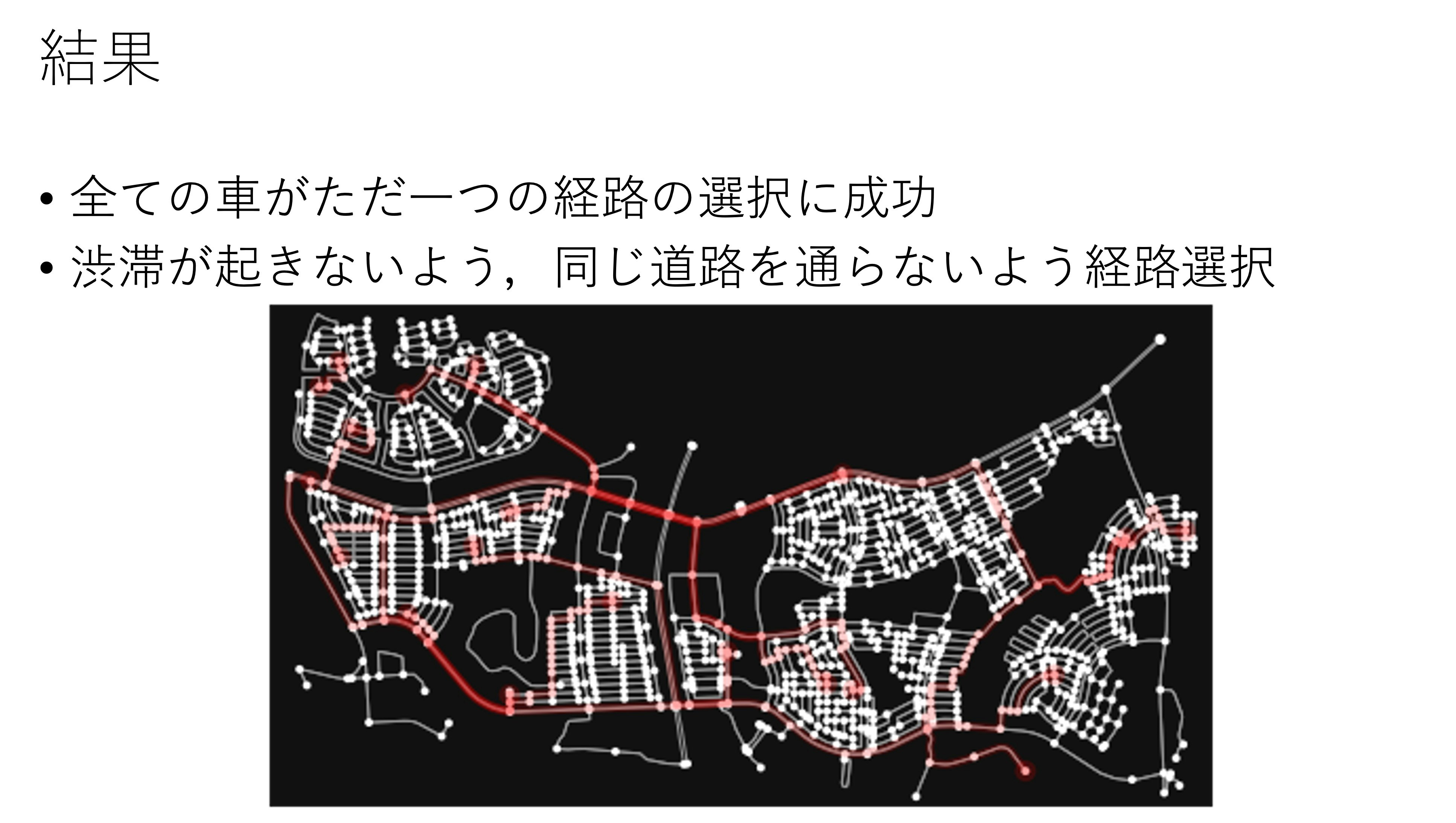
EV割り当て・スケジューリング最適化

渋滞緩和最適化

まとめ

この記事ではソリューションコンテストで発表した内容を，発表動画には入りきらなかった部分の説明も込めて詳細に紹介してきました．
この記事を書いている2021/12/10現在ではまだ結果は出ていませんが，結構いい線行ってるのではないかと思います．
結果がわかれば情報をアップデートできればいいなと思っております．

また，繰り返しですがこの記事の内容について，YouTube動画が出ています！是非ご覧ください！

最後にQuantumPredatorのメンバーと，ここまでこの記事を読んでいただいた皆さん，本当にありがとうございました．