Sqrt treeの日本語の解説記事がなかったので書きます.
ネタバレをすると,このデータ構造はあまり使えません.しかし,面白いデータ構造だと僕は思います.
この記事中で「積」という言葉を頻繁に使いますが,これは掛け算とは限らず一般に二項演算の結果を指します.あと二項演算を$*$で表すことにします.
目次
Sqrt tree is 何
Sqrt treeは,半群の静的な列の区間積を高速に計算するデータ構造である.同じく半群の静的な列を扱うスパーステーブルや Disjoint sparse table (DST) の上位(?)互換となる.
半群とは,集合と結合的な二項演算を合わせた代数的構造である.セグメント木にモノイドが乗ることは有名だが,半群はモノイドから単位元を取ったもの.このため,セグメント木よりも広い範囲の対象を扱うことができる.
(半群に適当な単位元を添加してモノイドに拡張することでセグ木に乗せることができるが,Sqrt treeでは何も考えなくても半群を直接扱えるという話)
Sqrt treeの時間計算量は構築とクエリが $<O(n\lg\lg n),\ O(1)>$,空間計算量は $O(n\lg\lg n)$ となっている.これは,
- 平方分割 $<O(n),\ O(\sqrt{n})>$
- セグメント木 $<O(n),\ O(\lg n)>$
- スパーステーブル/DST $<O(n\lg n),\ O(1)>$
と比べると,かなり良い計算量であることがわかる.
Sqrt treeは以下のCodeforcesの記事で導入された.
Sqrt-tree: answering queries in O(1) with O(NloglogN) preprocessing.
この記事の解説パートは半分くらいは上の記事の翻訳.
仕組み
1. 平方分割の改良
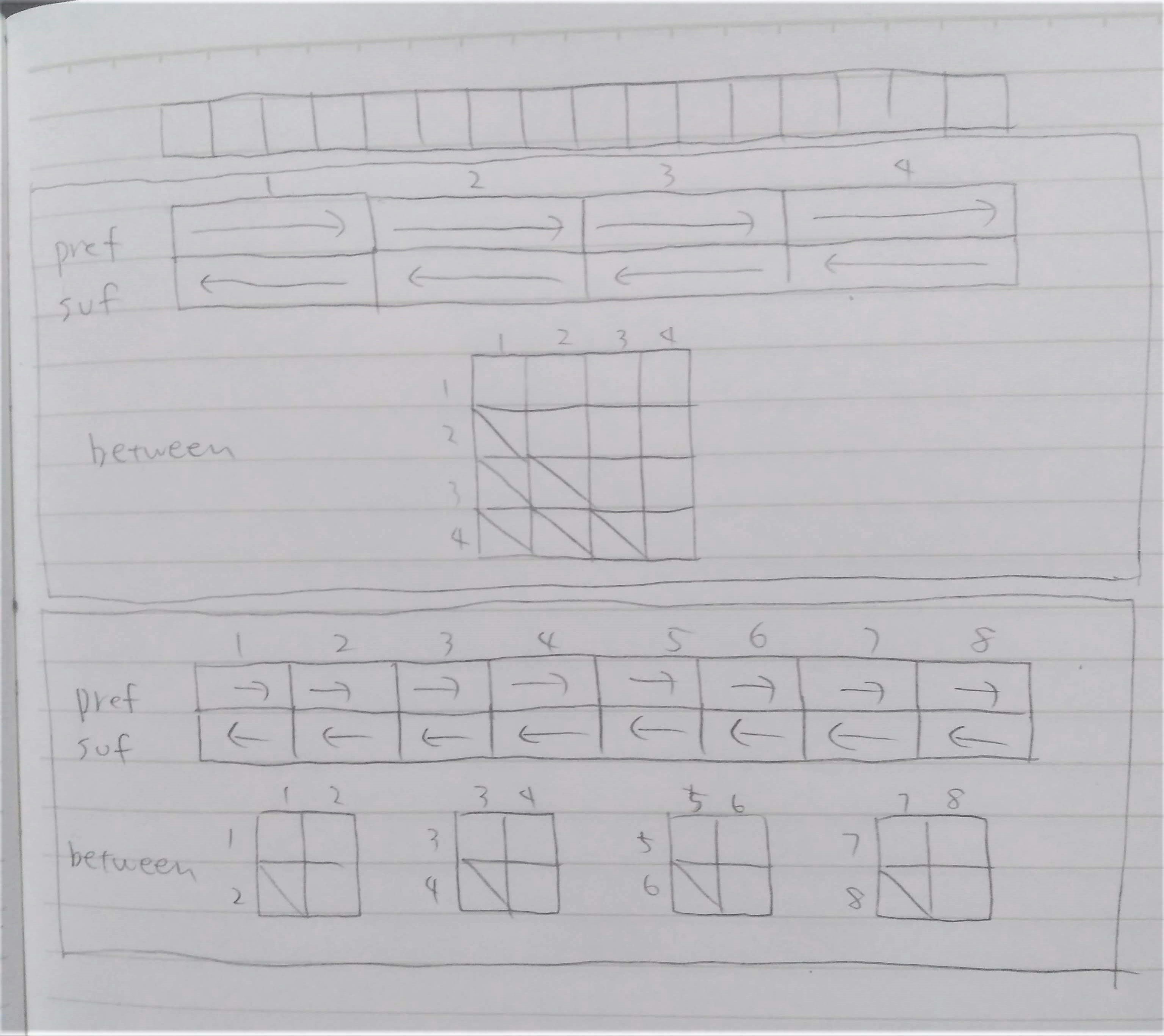
平方分割は,列に対するクエリを扱う一般的な手法である.列をサイズ $b$ のブロックに分け,各ブロック内の要素の総積を計算する.区間に対するクエリが飛んできたら,区間に完全に覆われているブロックの総積と,ブロックからはみ出す要素の総積を計算する.ブロックは全部で $O(\frac{n}{b})$ 個,はみ出す要素は $O(b)$ 個あるので,計算量は $O(\frac{n}{b} + b)$ となる.ここで, $b = \sqrt{n}$ とすることで,計算量を $O(\sqrt{n})$ にすることができる.
ここで,ブロックをまたいだクエリに注目すると,計算しているのは常に(左端のブロックの接尾辞積),(2ブロック間の総積),(右端のブロックの接頭辞積)となっている.そのため,
- 接頭辞積 $pref(i)$ ($i$番目の要素から,それを含むブロックの左端まで総積)
- 接尾辞積 $suf(i)$ ($i$番目の要素から,それを含むブロックの右端までの総積)
- 2ブロック間の総積 $between(i, j)$ ($i$番目のブロックから$j$番目のブロックまでの総積)
を前計算しておくことで,$[l, r]$ へのクエリに $suf(l) * between(\frac{l}{b} + 1, \frac{r}{b} - 1) * pref(r)$ を計算するだけで $O(1)$ 時間で答えることができる.ここで,ブロックは $O(\sqrt{n})$ 個あるので,構築時にすべてのブロック間の総積を計算しても $O(\sqrt{n}^2) = O(n)$ に収まる.
しかしこの手法では,1つのブロックに完全に収まるクエリに対しては,前計算した値が使えないので,依然$O(\sqrt{n})$時間かかってしまう.
2. 再帰的な平方分割
ブロックをまたいだクエリには高速に答えられるので,ブロックを細かくしていくと高速に答えられる区間が増えそうである.そこで,平方分割してできたブロックをさらに平方分割してみる.
1回目の平方分割のブロックの大きさは $O(\sqrt{n})$ だったので,2回目の平方分割のブロックの大きさは $O(\sqrt{\sqrt{n}}) = O(n^\frac{1}{4})$ となる.2回目の平方分割でできたブロックにも同様に $pref, suf, between$ を計算することで,ブロックをまたぐクエリに答えることができる.
この時点ですでに $<O(n),\ O(n^\frac{1}{4})>$ の時間計算量を達成しているが,せっかくなのでこれ以上平方分割できなくなるまで平方分割を続けてみる.
ブロックの大きさが3以下になると,それ以上の平方分割は意味を成さない.ここまで小さくするまでに,何回の平方分割が必要だろうか.1層目では $n^{\frac{1}{2}}$ 個のブロック,2層目では $n^{\frac{1}{4}}$ 個のブロック,$k$ 層目では $n^{\frac{1}{2^k}}$ 個のブロックができることになるので,全部で $O(\lg\lg n)$ 層できることになる.
$\lg\lg n$ というのは,非常に成長が遅い関数である.$\lg\lg 10^6 \leq 5$ なので,実質定数と考えてもよい.この木の浅さが,Sqrt treeの速さの秘訣となっている.
計算量を見ていこう.$O(\lg\lg n)$ 層あって,1つの層の計算に $O(n)$ 時間かかるので,構築は $O(n\lg\lg n)$ かかることになる.クエリは,まずどの層を使うかを1つ1つみると $O(\lg\lg n)$ 時間かかる.層が特定できれば,クエリには $O(1)$ 時間で答えられるので,全体で $O(\lg\lg n)$ となる.使う層を二分探索すれば $O(\lg\lg\lg n)$ でできる.十分すぎるほど高速だが,せっかくなので $O(1)$ でやりたい.
3. クエリのさらなる高速化
スパーステーブルやDSTがクエリを処理する仕組みを考えてみると,どちらも2冪のまとまりで列を見ていって階層構造を作り,ビット演算を利用して使う層を特定することで高速にクエリを処理していた.Sqrt treeでも,似たような仕組みで層を特定できないだろうか?
まずビット演算を利用しようと思ったらブロックの大きさは2冪であることが望ましいので,ブロックの大きさを2冪で統一する.
大きさ $2^k$ のブロックを平方分割することを考える.$k$ が偶数の時は,大きさ $2^\frac{k}{2}$ のブロックを $2^\frac{k}{2}$ 個作ることができる.しかし $k$ が奇数の時に普通に平方分割をすると,大きさが2冪でなくなってしまう.ここで,代わりに大きさ $2^{\lceil \frac{k}{2} \rceil}$ のブロックを $2^{\lfloor \frac{k}{2} \rfloor}$ 個作ることにする.こうしても計算量は変わらない.
区間 $[l, r]$ が大きさ $2^k$ のブロックに完全に収まるとき,$l$ と $r$ は下位 $k$ ビットだけが異なり,他は同じになる.逆に,$l$ と $r$ の $k$ ビット目以降が異なるとき,その区間は大きさ $2^k$ のブロックをまたぐことになるので,その層で扱える.そのため,$l \oplus r$ の msb を計算して,それよりもブロックのサイズが小さい層の中で最も浅いものが使うべき層になる.これは適切な前計算をすることで $O(1)$ で実現することができる.
実装例
基本的にCodeforcesの記事の実装を参考にした.個人的な好みでいろいろ改変している.
本家の実装はシフト演算を多用していてわかりにくかったので,掛け算割り算に直してすっきりするところは直した.また,構築を非再帰にした.あとは変数名とかを自分好みに改変した.半群を構造体で渡す設計にしてある.
# include <algorithm>
# include <vector>
template <typename S>
class SqrtTree {
using T = typename S::T; // type of the semigroup
public:
SqrtTree() = default;
explicit SqrtTree(const std::vector<T>& v) : v(v) {
int n = v.size(), lg = 0;
while ((1 << lg) < n) ++lg;
on_layer.resize(lg + 1);
int n_layer = 0;
for (int i = lg; i > 1; i = (i + 1) / 2) {
on_layer[i] = n_layer++;
layer_lg.push_back(i);
}
for (int i = lg - 1; i >= 0; --i) on_layer[i] = std::max(on_layer[i], on_layer[i + 1]);
pref.resize(n_layer, std::vector<T>(n));
suf.resize(n_layer, std::vector<T>(n));
btwn.resize(n_layer, std::vector<T>(1 << lg));
for (int layer = 0; layer < n_layer; ++layer) {
int prev_b_sz = 1 << layer_lg[layer];
int b_sz = 1 << ((layer_lg[layer] + 1) / 2);
int b_cnt = 1 << (layer_lg[layer] / 2);
for (int l = 0; l < n; l += prev_b_sz) {
int r = std::min(l + prev_b_sz, n);
// calculate pref and suf
for (int a = l; a < r; a += b_sz) {
int b = std::min(a + b_sz, r);
pref[layer][a] = v[a];
for (int i = a + 1; i < b; ++i) {
pref[layer][i] = S::op(pref[layer][i - 1], v[i]);
}
suf[layer][b - 1] = v[b - 1];
for (int i = b - 2; i >= a; --i) {
suf[layer][i] = S::op(v[i], suf[layer][i + 1]);
}
}
// calculate btwn
for (int i = 0; i < b_cnt; ++i) {
T val = suf[layer][l + i * b_sz];
btwn[layer][l + i * b_cnt + i] = val;
for (int j = i + 1; j < b_cnt; ++j) {
val = S::op(val, suf[layer][l + j * b_sz]);
btwn[layer][l + i * b_cnt + j] = val;
}
}
}
}
}
T fold(int l, int r) const {
--r;
if (l == r) return v[l];
if (l + 1 == r) return S::op(v[l], v[r]);
int layer = on_layer[32 - __builtin_clz(l ^ r)];
int b_sz = 1 << ((layer_lg[layer] + 1) / 2);
int b_cnt = 1 << (layer_lg[layer] / 2);
int a = (l >> layer_lg[layer]) << layer_lg[layer];
int lblock = (l - a) / b_sz + 1;
int rblock = (r - a) / b_sz - 1;
T val = suf[layer][l];
if (lblock <= rblock) val = S::op(val, btwn[layer][a + lblock * b_cnt + rblock]);
val = S::op(val, pref[layer][r]);
return val;
}
private:
std::vector<int> layer_lg, on_layer;
std::vector<T> v;
std::vector<std::vector<T>> pref, suf, btwn;
};
発展: 更新クエリ
今まではSqrt treeを静的な列を扱うデータ構造として見てきたが,列の更新にも対応できるように改変できる.
列の要素を1つ変更したときに影響される部分は,一層目では $O(n)$ 箇所,2層目では $O(\sqrt{n})$ 箇所,...となるので,全体で $O(n)$ 箇所を変更する必要がある.平方分割では $O(\sqrt{n})$ で済んだが,Sqrt treeの場合は $between$ を変更する必要があるので,$O(n)$ になってしまう.
ここで,2層目以降は$O(\sqrt{n})$で更新できるから,ボトルネックとなっている1層目の $between$ を高速に更新する方法を考える.
$between$ はブロック間の要素の総積だから,ブロックを各要素とする列の区間クエリとみなすことができる.そこで,1層目の $between$ もSqrt treeで管理することにしよう.1層目のブロックの個数は $O(\sqrt{n})$ 個なので,これは $O(\sqrt{n})$ で更新することができる.これで,列の更新が $O(\sqrt{n})$ でできるようになった.
また,遅延伝搬を用いることで区間更新も可能になる.詳細は以下のCodeforcesの記事を参照.
Sqrt-tree (part 2): modifications in O(sqrtN), lazy propagation
実装はここでは示さないが,こちらの記事に実装例が載っている.元となる配列に1層目のブロックの値を追加して扱っている.
このようにして更新クエリの処理が可能となるが,個人的には,Sqrt tree は静的な列を扱うデータ構造として捉えたい.更新クエリは実装が面倒な上,$O(\sqrt{n})$ はセグメント木などの $O(\lg n)$ に比べて遅く,更新が必要ならセグメント木を使用するべきだ.取得クエリが更新クエリに比べてはるかに多い場合などは有用になるかもしれないが,少なくとも競技プログラミングにおいてはわざわざSqrt treeで更新クエリを実現することの利点は薄いと思われる.
発展: さらなる高速化(?)
実はSqrt treeの考え方を進めていくと,(理論的な)計算量がもっと落ちる.
列を $\sqrt{n}$ ではなく $\lg n$ のブロックに分割し,$between$ をDSTで管理する.木の高さは $O(\lg^* n)$ (iterated logarithm) となり,DSTの構築の計算量は $O(\frac{n}{\lg n}\lg \frac{n}{\lg n}) = O(n)$ となる.これで,全体で $<O(n\lg^* n),\ O(1)>$ で区間クエリを処理できる.
$\lg^*10^{19000} \approx 5$ です.はい.
ここまで来ると,これらのデータ構造には以下のような階層関係があることに気づく.
| レベル | 名称 | 計算量 | ブロックのサイズ | $between$の管理 |
|---|---|---|---|---|
| 1 | (ナイーブ) | $O(n^2)$ | ||
| 2 | DST | $O(n\lg n)$ | $\frac{n}{2}$ ($2n$ の逆関数) | |
| 3 | Sqrt tree | $O(n\lg\lg n)$ | $\sqrt{n}$ ($n^2$ の逆関数) | ナイーブ (レベル1) |
| 4 | ? | $O(n\lg^* n)$ | $\lg{n}$ ($2^n$ の逆関数) | DST (レベル2) |
| 5 | ? | ? | $\lg^*{n}$ ($^n2$ (テトレーション) の逆関数) | Sqrt tree (レベル3) |
| $k$ | ? | ? | ? (よくわからない関数の逆関数) | ? (レベル$k-2$) |
このことは以下の論文で詳細に述べられている.
OPTIMAL PREPROCESSING FOR ANSWERING ON-LINE PRODUCT QUERIES
この論文では,区間積クエリを$k$ステップの計算で答えるアルゴリズムについて考えている.ここでいう$k$ステップとは,$k$個の前計算した値の積を取ることでクエリに答えることを指す.ナイーブは$k=1$,DSTは$k=2$,Sqrt treeは$k=3$である.$\lg n$のブロックに分割するやつは,$pref, between, suf$の3つの積を取っているが,$between$の計算にDSTを使うためここに2ステップ使い,合計4ステップ,$k=4$となっている.
前計算の計算量とステップ数はトレードオフの関係になっている.ステップ数を増やすと構築の計算量は落ちるが,クエリの定数倍が重くなる.
$k$ステップでクエリに答えるのは,上の表に示したアルゴリズムが理論的な下限であることがこの論文で証明されている.また論文では$<O(n),\ O(\alpha(n))>$のアルゴリズムが提示されており,それが理論的な下限であることも示されている ($\alpha(n)$はアッカーマン関数の逆関数).列をサイズ$\alpha(n)$のブロックに分割し,$2\alpha(n)$ステップのアルゴリズムを使うとできるらしい.
実験
Sqrt treeの速さを実際に測ってみる.
実験1. RmQ
Sqrt tree を利用して数列の区間最小値を求める Range Minimum Query (RmQ) が実現できる.
yosupo judgeの Static RMQ を用いて速度の比較をする.
| データ構造 | 実行時間 | メモリ使用量 | 提出 |
|---|---|---|---|
| Sqrt tree | 181 ms | 39.58 MiB | https://judge.yosupo.jp/submission/28826 |
| スパーステーブル | 190 ms | 42.97 MiB | https://judge.yosupo.jp/submission/28827 |
| DST | 198 ms | 44.89 MiB | https://judge.yosupo.jp/submission/28829 |
| セグ木 | 179 ms | 10.61 MiB | https://judge.yosupo.jp/submission/28830 |
実行速度はどれもほとんど同じで,気持ちセグ木とSqrt treeが速い感じ.セグ木がここまで速いのは想定外だった.
メモリ使用量はセグ木の圧勝.他と比べて4倍くらい違う.Sqrt treeはスパーステーブル系に比べて若干メモリ使用量が少ないが,ほとんど同じ.理論的には空間計算量が改善されているが,定数倍が重いため,スパーステーブルとほとんど一緒になってしまう.
セグ木の素晴らしさを実感した実験1だった(?).
実験2. RSQ
区間和もできる.
yosupo judgeの Static Range Sum を用いて速度の比較をする.
| データ構造 | 実行時間 | メモリ使用量 | 提出 |
|---|---|---|---|
| Sqrt tree | 215 ms | 77.78 MiB | https://judge.yosupo.jp/submission/29130 |
| DST | 230 ms | 88.29 MiB | https://judge.yosupo.jp/submission/29131 |
| セグ木 | 204 ms | 19.80 MiB | https://judge.yosupo.jp/submission/29132 |
| Fenwick tree | 164 ms | 15.55 MiB | https://judge.yosupo.jp/submission/29133 |
| 累積和 | 169 ms | 15.62 MiB | https://judge.yosupo.jp/submission/29134 |
Fenwick tree が累積和より速いの,何?
やはりセグ木系は実行時間,メモリ使用量ともに素晴らしい.Sqrt treeは,DSTに対しては優位性を示した.若干実行時間が早くなっているし,メモリ使用量の差は顕著に出た.
まとめ
タイトル詐欺をして申し訳ございませんでした.
Sqrt treeの仕組みはなかなか面白く,理論的な計算量もよいが,残念ながら競技プログラミングにおいては実装の重さと定数倍の大きさを考えると他のデータ構造に対するメリットは薄い.
しかしせっかく書いたので,僕はSqrt treeをコンテストで積極的に使っていきたいと思います.