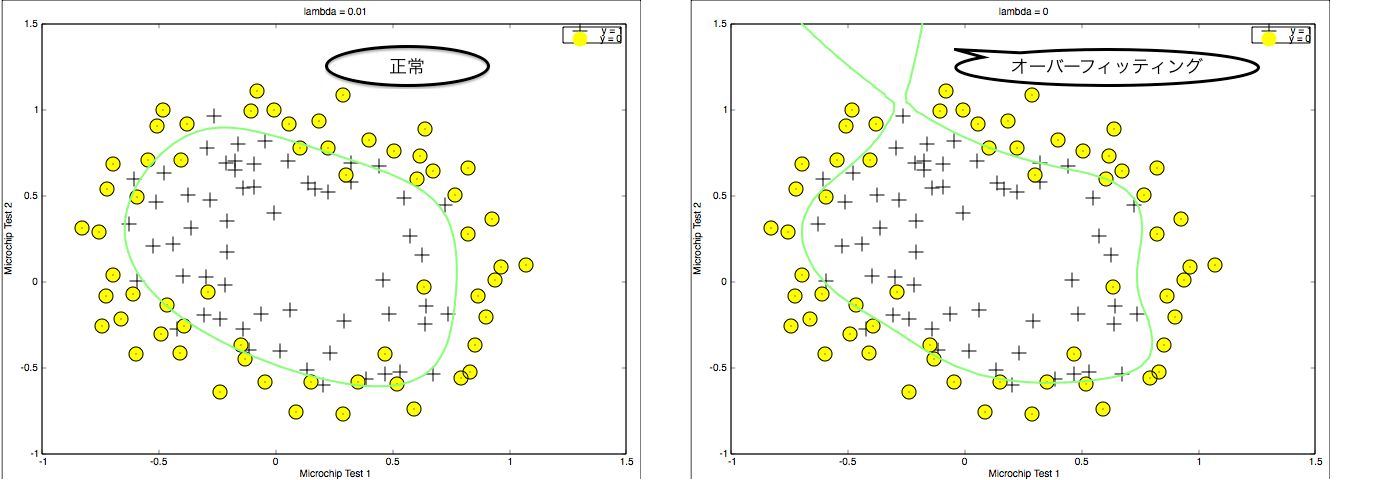
本記事では、こちらのサイト を参考にオーバーフィッティング(Overfitting)と、それを克服する正則化(Regularization)について解説します。
オーバーフィッティングと正則化
オーバーフィッティングとは
一般的にトレーニングセットにはノイズが含まれます。学習時にノイズの影響を受けることで、トレーニングセットには適合できるが、未知データには適合できなくなることをオーバーフィッティング・過適合といいます。(トレーニングセットにも適合しないことをアンダーフィッティング・高バイアスと言います。)
対策の例
- 出力に有効でない変数を減らす。(例えば、他の変数の関数になっているもの)
- 正則化
正則化
正則化とは、コスト関数に罰則を加えた新しいコスト関数を用いることで、モデルの複雑さを緩和しようとするための手法です。決めるべきパラメータが $\theta = \left(\theta_0, \theta_1, \ldots , \theta_n \right)^T$ であるモデルの従来のコスト関数を $\tilde{\mathrm{Cost}}(\theta)$ とします。例えば、確率変数の大きさという複雑さを緩和する方法が次の正則化1です。
\mathrm{Cost}(\theta) = \tilde{\mathrm{Cost}}(\theta)+ \lambda \sum_{i=1}^{n}\theta_i^2
ここで、 $\lambda (> 0)$ は正則化パラメータと呼ばれます。2 正則化した後は左辺の $\mathrm{Cost}(\theta)$ を最小化する $\theta$ を求めることになります。
正規方程式
トレーニングセット $(x_i, y_i),\ 1 \leq i \leq m$ と $\tilde{x_i} := (1, x_i)^T$ に対して、線形回帰の二乗誤差の正則化問題
\mathrm{Cost}(\theta) = \frac{1}{2m}\sum_{i=1}^m \left( \theta \cdot \tilde{x_i} - y_i \right)^2 + \frac{\lambda}{2m} \sum_{i=1}^{n}\theta_i^2
は3
X =
\left(
\begin{array}{c}
(\tilde{x_0})^T\\
(\tilde{x_1})^T\\
\vdots \\
(\tilde{x_n})^T
\end{array}
\right)
とおくと、解析的に
\theta = \left( X^TX + \lambda
\left(
\begin{array}{cccc}
0&0&\cdots&0\\
0&1&\cdots&0\\
\vdots & \vdots&\ddots & \vdots\\
0 & 0& \cdots&1
\end{array}
\right)
\right)^{-1}X^T y
という解を得ます。これ4を正規方程式(Normal equation)といいます。ただし、 $\lambda = 0$ のときは右辺の $X^TX$ に逆行列の存在が保障されていないことに注意してください。5