ゲージ理論 ああゲージ理論 ゲージ理論 （数学編）

はじめに

皆さん、今年の流行語大賞はご存知でしょうか？僕が流行に疎いせいか最近の流行語を聞いてもいまいちピンときません。Wikipediaによるとどうやら流行語は『現代用語の基礎知識』（自由国民社・刊）の読者アンケートの結果が起因しているそうです。何それ聞いたことない、、 果たしてその読者層は最近の流行に乗っている層なのでしょうか？僕にはそう思えません。
では、誰がどこで日本の流行を生み出しているのか...
いつの時代も流行は若者が作り出すものです。若者の街といえば渋谷！
そして若者の集い場といえば大学！
きっと渋谷にある大学に通うイケイケ¹大学生聞けば間違い無いでしょう。そう思いとある大学で街頭調査を行いましたのでその結果を発表します。

第3位　清水統計　（10票）

まあやっぱりランクインするよね。今年のベストセラーです。

第2位　イジング模型　（11票）

いやー清水統計と僅差でしたねぇ。ノーベル賞の影響もあってか確かに今年はよく聞いた記憶があります。

ではでは栄えある第一位の発表に移りましょう。

第1位　ゲージ理論　(110票)

ですよねぇ。やっぱりという結果です。駒場の各所で話題が上がっていました。おめでとうございます👏

ご覧のように、今年の流行語はゲージ理論と納得のいく結果が出ましたね。ですが、中には「流行に疎くて聞いたことないよ」という方もいらっしゃるかもしれません。
そんなあなたのためにこの記事を通してゲージ理論とは何かについてまとめていこうと思います。
この記事を読んであなたも一緒に時代の風に吹かれましょう！

もくじ

数学編
-ゲージ理論にできること
-ゲージ理論の気持ち
-物理→数学への翻訳
-共変微分
-数物間の言葉の対応
-あとがき（数学）
-脚注

ちょっぴり長くなってしまったので前編後編に分けました。
前編が数学、後編が物理によっています。後編にもまとめを載せたので、物理に興味がある方や結論を先に見たい方は先に後編を読んでも大丈夫です。

物理編
-はじめに
-物理的な要請とその結末
-"電磁気学C" ~U(1)ゲージ理論~
-余ったトピック
-まとめ

ゲージ理論にできること

ゲージ理論とは何か？天文学会による天文学辞典にはこのように書いてあります。

素粒子の相互作用（素粒子間に働く力：四つの力を参照）の記述に際し、ゲージ変換に対して作用が不変であるという要請を取り入れた理論のことをゲージ理論と呼ぶ。今日では、電磁相互作用だけでなく、弱い相互作用（弱い力）、強い相互作用（強い力）、重力相互作用（重力）を合わせた4つの相互作用（力）がすべてゲージ理論で表現できることが知られている。（一部抜粋） ²

辞書の想定読者であろう言葉の意味を知らない人にとっては何も説明になっていない説明に加え、何やら後半には面白いことが書いてあります。
"4つの力全てがゲージ理論で表現できる"
なんとも魅力的な主張ですね。
世にある4つの力の電磁気力・弱い力・強い力・重力、、
どれも個性的に見える四つの力がゲージ理論では統一的に扱えるようです。実際にこの主張は正しく、力に対する新たな視点を与え、4つの力の統一的な解釈ができます。
また、ある意味で力を導出することができます。物理学において力はとっても身近な概念で、力の出てこない分野はないでしょう。中学生でもなんなら小学生、幼稚園生でも力という概念は知っています。こんな誰もが知っている力ですが "力ってなぁに？" と小学生に聞かれたら困ってしまいます。
とても馴染み深い概念 "力" ですが、よくよく考えると物理学においてほとんどの分野は力（相互作用）は天下り的に与えられるもので、与えられた力のもとでどのような現象を見せるかや運動から力の関数を解析することが大半です。
ところがゲージ理論はその ”力とは何か” という問いに対して迫っていく理論です。ゲージ理論を学ぶことで力に関する新たな理解を得ることができます。
ゲージ理論に対して興味を持っていただけたでしょうか？この記事ではそんな魅力的で美しいゲージ理論に関しての解説を行っていこうと思います。

前提知識・想定者層

ここでこの記事の想定読者、前提知識に関してここで言及しておきましょう。

目標としては大学一年生、去年の自分でも読めるようにと心がけて書きました。かの有名なFeynmanは「高校生に説明できないのならそのことを本当に理解したとは言えない」と言ったそうです。紙面の都合上、全てを一から説明することはできませんでしたが、去年の自分に読ませて理解ができるようには仕上げたつもりです。さらに一年生は今まさに電磁気学を習っているところでしょう。高校では各論的だった電磁気の公式が4つのMaxwell方程式から全て導けることに感動した人も多いと思います。はたまたもう少し勉強をしてゲージポテンシャルや微分形式を用いその式を一本にまとめ、その美しさに感動したことのある人もいるでしょう。今回の話はそれらの話の最終形態に当たり、電磁気学をある真っ当な原理から導きます。 （その原理はゲージ原理と呼ばれています）是非楽しみにしていてください。難しい言葉が出てきて一瞬怯んでしまうかもしれませんが、言葉は本質ではありません。ややこしくなったら飛ばしても耐える（？）ように書いたつもりです。
ゲージ理論は原理は素朴、理論はシンプルでいて結論は圧倒的です。最後までついてくればきっと一緒にゲージ理論の美しさに想いを馳せることができるでしょう。

加えて普段は数学を主に勉強されている方にもぜひ読んで欲しいと思っています。ゲージ理論は数学的に非常に綺麗に書かれています。さらに最近では数学方面からゲージ理論の言葉が聞こえることも多いです。³ゲージ理論は数学者も含む色々な背景を持った人たち⁴が知恵を振り絞り相補的に発展した（そして現在も発展している）分野です。今回は要所要所で数学の言葉、物理の言葉を導入しそれらの対応関係を見ていきます。この記事を通してそれぞれの分野の人が他方の分野に興味を持ってくだされば、統合自然科学科数理コースの者の身⁵として嬉しい限りです。

最後にこの記事の目的をまとめると

本記事の目的
ゲージ理論を理解して
・4つの力を統一的に扱う
・電磁気学を導く
・数学と物理の双方の言葉の対応をみる

となります。
ある本には「ゲージ理論の美しさから、物理学者は皆ゲージ理論教に入信している」との記述があります。⁶そんなゲージ理論を次章からは精一杯布教していこうと思います。

ゲージ理論の気持ち　〜基底によらない物理を目指して〜

まず一番初めにゲージ理論の思想について話してしまおうと思います。ゲージ理論の思想とはズバリ物理法則は人間の見方に依らないということです。世界に物理的な事実は、誰がどのように見たかなどに依存してはならないという話です。この話を時空について慣性系にいる観測者（基底）についての座標変換について論じたものが特殊相対論、一般の観測者（基底）について論じたものが一般相対性理論であります。
この思想を時空だけではなく、場の空間（数学ではファイバーといいます）に関して論じたものがゲージ理論であります。未定義語がたくさん登場して何を言っているのかよくわからないと思います。それをきちんと整備するために「数学の言葉を用いて、主張を明確にすること」がこの記事、数学編の目標であります。
感覚的に真っ当な主張を元に議論を進めると、最初に書いたような四つの力が導かれます。力と聞いた時に基底や座標変換が思い浮かぶ人はまずいないでしょう。実はそれらが力の根源であるとはなんとも不思議ですね。

コラム　物理の幾何学化
もう少しここで議論した話をフォーマルにすると、座標によらない物理をすることは、物理学の幾何学化と見ることができます。座標なしに依然として存在する幾何学的な物体は、座標を人間が敷いたところでそれにより影響を受けません。目の前にあるおにぎりが座標を変えたらサッカーボールになってしまったら嫌ですね。同じように、物理学でも人間が敷く座標と無関係に存在するものがあります。座標なんて非本質なのですが、座標を使うとなんだか落ち着きますし、扱いやすくなります。
このような座標によらない実態への意識を明確にするために、さまざまな物理を幾何学的に行おうという試みがあります。例えば山本・中村「解析力学」などが有名です。今回の話に当てはめると、時空の幾何学化が相対論、相互作用の幾何学化がゲージ理論です。
この試みは数学的に美しく、視界がクリアになるというメリットもありますが、ゲージ理論の場合はそこから大抵の理論ではその実態は扱えなず未知のものであった力に対して新たな興味深い描像が得られます。

物理→数学への翻訳

この章は単なる言葉の紹介です。ここから先の章を読む際に辞書のように使ってください。ここだけでよくわかることはまずないので、ふむふむと思いながら流し読みする程度がいいでしょう
混乱した場合はきっと僕の書き方が雑なことが原因です。参考文献にあげるような教科書を読むことをお勧めします。

ゲージ理論では対称性が重要です。対称性とは変換不変性と言い換えることができます。変換について考える際には、数学の言葉を使うのが適していますね。ということで物理で普段扱う対象を数学に落とし込もうという話をしていきます。
結論を先に述べると、数学のファイバー束という概念を使います。

まずは普段の物理で何をしているかを考えてみましょう。
物理では何かのダイナミクス（時間発展）を予測することが目標です。
例えば力学では、時間発展を追って質点の運動を予測しますね。量子力学では空間を引数にもつ波動関数の時間発展を追います。また、それを拡張した場の量子論では、時空全てをパラメタとして場の変化を追います。

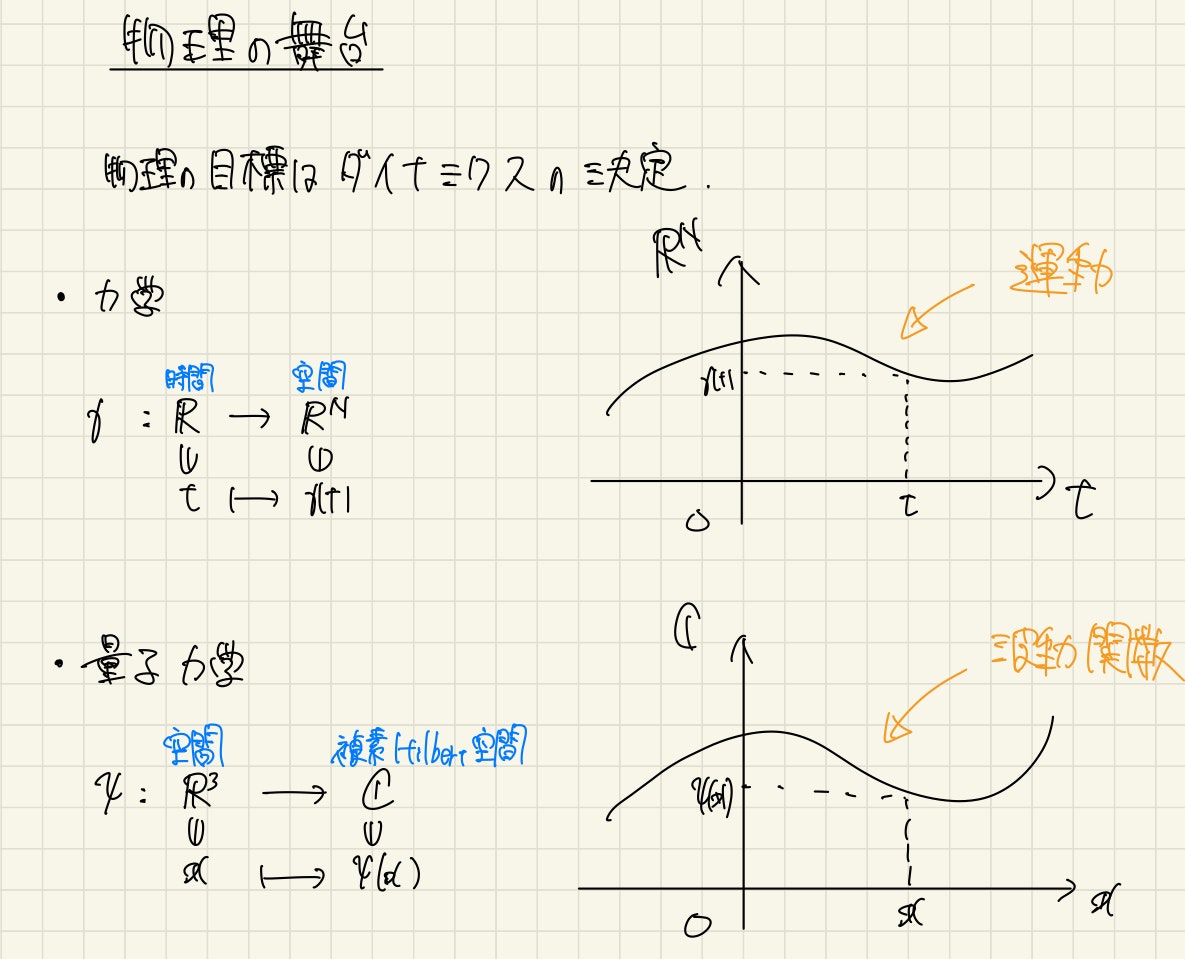
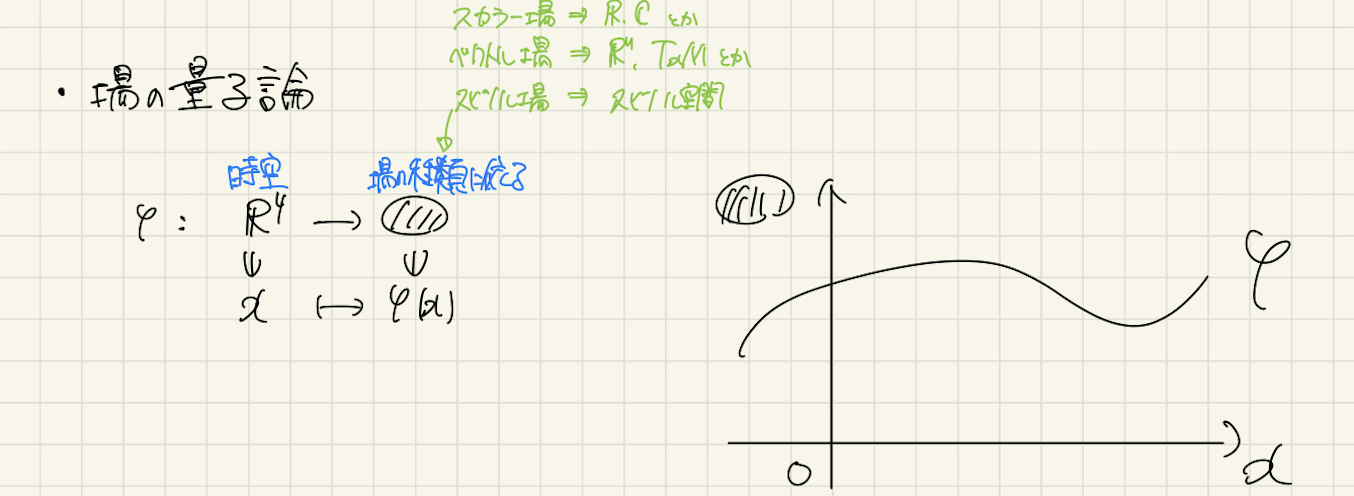
こう並べてみるとどれらも関数（運動、波動関数、場）のパラメタ（時間、空間、時空）による変化を追うという似た構造を持っていると思えてきませんか？
これらを数学の言葉（ファイバー束の理論）に置き換えると以下のようになります。

物理	数学
パラメタ	底空間
関数	切断
関数が値を取る空間	ファイバー

単なる言葉の言い換えです。もう少し馴染み深い例としてはグラフの一般化というのがいいでしょう。$xy$平面での関数$y=f(x)$をファイバー束の言葉で言えば$x\in \mathbb{R}$が底空間、値域$y\in \mathbb{R}$がファイバー、関数$f$がその切断です。逆にこの例から引数の入っている空間が底空間、値域がファイバー、その上の関数が切断です。
少しでもファイバー束に馴染んでいただけたら嬉しいです。

また、物理ではよく観測者を取り替えること（座標変換）をしますね。基本的にはパラメタの表示を取り替えて、それに伴う関数の変化について考えていましたね。底空間（多様体）の言葉で言えば、局所座標表示の取り替えです。同様のことをファイバーの話でも考えてみましょう。

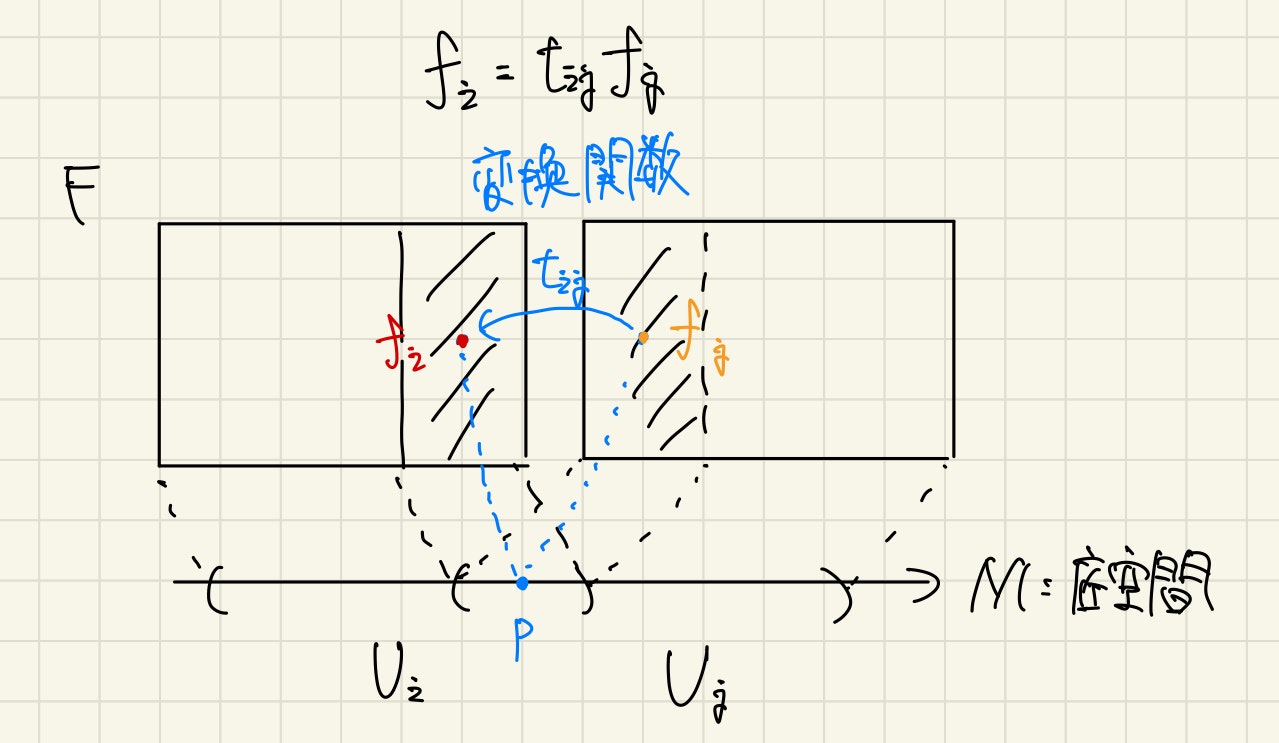
上のような$t_{ij}$のことを変換関数と呼びます。これは群の満たす性質を満たすので群になっています。底空間で異なる局所座標$U_i$,$U_j$を取った際のファイバーでの値を$f_i$,$f_j$とかけばそれらが

f_i = t_{ij} f_j

と変換するということです。
不要なことを省略してしまったのですが、これらの性質が矛盾なくそして無駄なく定義したものがファイバー束です。
定義はこのようになっています。

今回は紹介しなかった言葉がずらりと並んでギョッとするかもしれませんがあまり気にしないでください。そこまで深い知識はこの記事を読む程度では必要ありません。
上で紹介したように、ファイバー束とはグラフ$y=f(x)$の一般化で

物理	数学
パラメタ	底空間
関数	切断
関数が値を取る空間	ファイバー

の言葉の置き換えさえ知っていれば十分です。

共変微分　〜基底が変わると起こること〜

次にファイバー上での微分を考えます。ファイバーとは、底空間上の点を指定すれば、その上のファイバー空間が定まるという関係でしたね。よくよく考えれば実は異なる底空間の点で指定されるファイバー空間の間に関係はありません。そうなると微分を考える際に問題が起こります。微分とは、異なる2点の差を比べるものでした。今回は異なる2点は異なるファイバー、つまり異なる空間にあります。
例えば、異なるベクトル空間の元であるベクトルは比較することができませんね。
今回のファイバーでも同じように異なる2点の値に関係がないので、それらの間の情報を教えてあげる必要があります。それが接続です。
幾何学的な意味を述べれば、空間としては同型だとしても、その空間をどのように置くかの自由度があります。その自由度を固定するのが接続です。（隣と基底がどうずれたかを教えてあげるということです。）

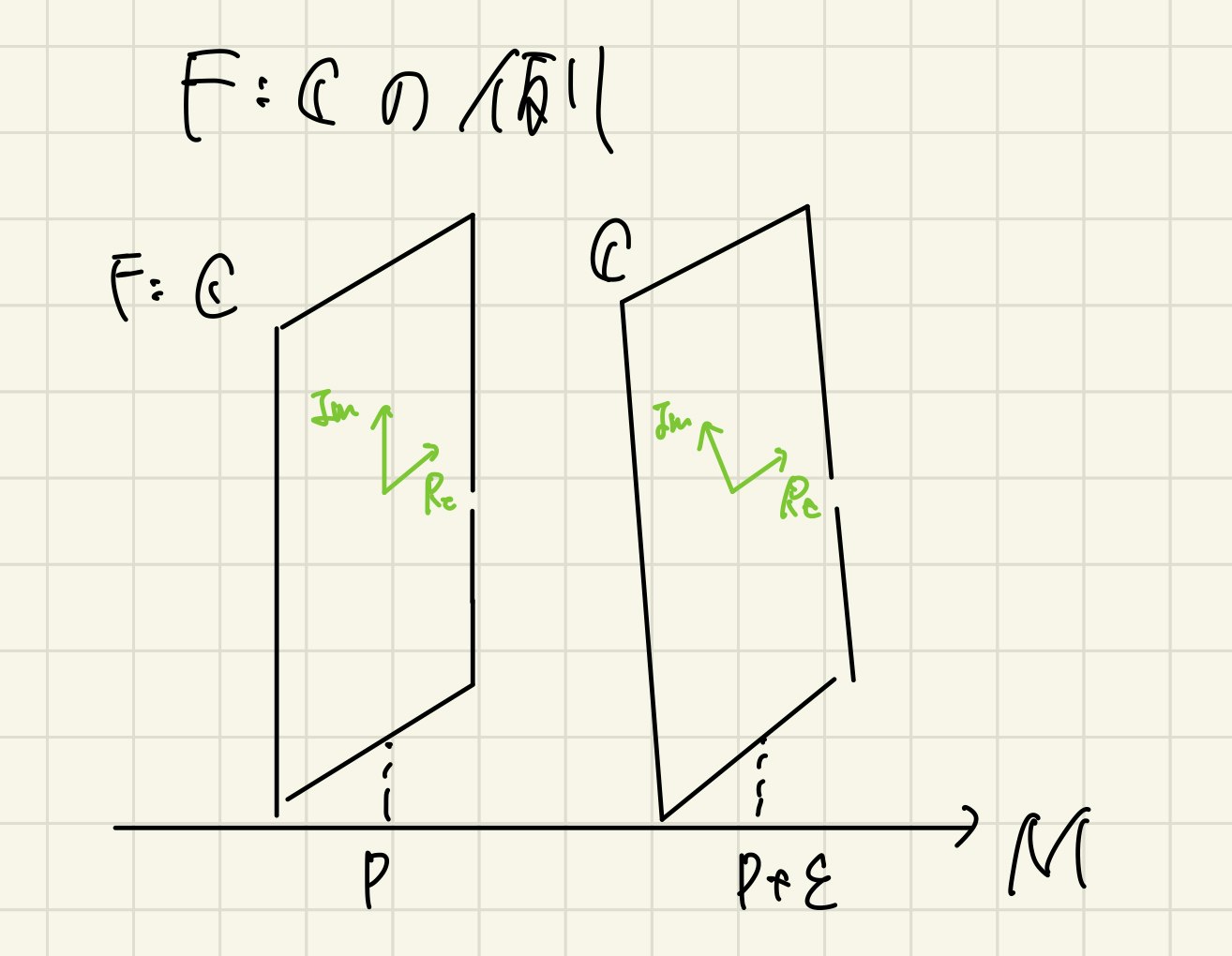
通常の微分では平坦な空間で行っていたため基底の変化について考える必要はありませんでしたが、今回は並行移動が自明ではないので基底の変化も含めて考える（チェーンルールを適用する）ことに対応しています。
具体的に書き表してみましょう。
幾何学的なベクトル場$\mathbf{u}(p)$（接ベクトルなどをイメージしてください）に対して底空間上の点$p$での成分表示を

\mathbf{u}(p)=u^{\mu}(p)\mathbf{e}_\mu(p)

と書きましょう。
そこから少しズレた点$p+\epsilon$では

\mathbf{u}(p+\epsilon)=u^{\mu}(p+\epsilon)\mathbf{e}_\mu(p+\epsilon)

となりますね。
このベクトル場の微分について考えましょう。
まず素朴に考えると、微分とは2点間の差とそのパラメタとの比の極限でありました。そのことから

\lim_ {\epsilon \to 0} \frac{\mathbf{u}(p+\epsilon)-\mathbf{u}(p)}{\epsilon}=\lim_{\epsilon \to 0}\frac{u^{\mu}(p+\epsilon)\mathbf{e}_{\mu}(p+\epsilon)
-u^{\mu}(p)\mathbf{e}_\mu(p)}{\epsilon}

としたくなりますが、先ほども述べた通り、${\mathbf{e}(p)}$と${\mathbf{e}(p+\epsilon)}$は異なるベクトル空間に住んでいるので、比べることができません。
異なる空間に住むベクトル同士を比較する手段が必要です。そこで以下の共変微分を導入します。困難は分割せよとのことで、ベクトル$\mathbf{u}$の基底$\mathbf{e}$についてまずは見ていきます。
新たに$p\to p+\epsilon$へ並行移動した$p$の基底$\mathbf{e}_{\mu ||}(p;\epsilon)$（空間としては底空間が$p+\epsilon$のものです）を

\mathbf{e}_{\mu ||}(p;\epsilon)=\mathbf{e}_{\mu}(p+\epsilon)-\epsilon \nabla_\beta \mathbf{e}_\mu |_{p+\epsilon}

と定義します。（pの基底からズレの1次項を加えました。）
ただし、

\nabla_\beta \mathbf{e}_\mu |_{p+\epsilon}=\mathbf{e}_\alpha (p+\epsilon) \Gamma ^{\alpha}_{\mu \beta}

と適当な係数$\Gamma^{\alpha}_ {\mu \beta}$を用いて$p+\epsilon$上の基底で展開できるとします。（$\nabla_{\beta}$と$\mathbf{e} _ {||} (p;\epsilon)$を上のように定義し、並行移動の効果を$\Gamma^{\alpha}_ { \mu \beta}$に押しつけています。）
この$\Gamma ^{\alpha}_ {\mu \beta}$が接続で、$\nabla_{\beta}$が共変微分です。
式を書き換えてまとめると、基底に関する共変微分 $\nabla_{\beta}\mathbf{e}_ {\mu}$がこのように

\nabla_\beta \mathbf{e}_\mu = \lim _{\epsilon \to 0} \frac{\mathbf{e}_\mu(p+\epsilon)-\mathbf{e}_{\mu ||}(p;\epsilon)}{\epsilon}=\mathbf{e}_{\alpha}(p+\epsilon)\Gamma^{\alpha}_{\mu \beta}

となります。

基底の変換則を定められたので、本題のベクトル場の微分を考えます。
我々は既に基底に関する微分規則を知っています。あとはそれに係数を引っ付けるだけなので簡単です。
$p \to p+\epsilon$へ並行移動したベクトルを同様に並行移動した基底でかくと

\mathbf{u}_{||}(p \to p+\epsilon)=u^{\mu}(p)\mathbf{e}_{\mu}(p;\epsilon)

これを用いて先ほどの共変微分をこのベクトルに作用させると

\begin{align}
\nabla_{\beta}\mathbf{u}
&=\lim_{\epsilon \to 0}\frac{\mathbf{u}(p+\epsilon)-\mathbf{u}_{||}(p)}{\epsilon}\\
&=\lim_{\epsilon \to 0}\frac{u^{\mu}(p+\epsilon)-u^{\mu}(p)}{\epsilon}\mathbf{e}_{\mu}(p+\epsilon)+u^{\mu}(p)\Gamma^{\alpha}_{\mu \beta}\mathbf{e}_{\alpha}(p+\epsilon)\\

&=(\partial_{\beta}u^{\mu})\mathbf{e}_{\mu}+u^{\mu}\Gamma^{\alpha}_{\mu \beta}\mathbf(e)_{\alpha}\\
&=(\partial_{\beta}u^{\mu}+u^{\alpha}\Gamma^{\mu}_{\alpha \beta})\mathbf{e}_{\mu}
\end{align}

ご覧のように二行目の式は

\nabla_{\beta}\mathbf{u}=
(\nabla_{\beta}u^{\mu})\mathbf{e}_{\mu}+u^{\mu}(\nabla_{\beta}\mathbf{e}_{\mu})

と読めます。つまりベクトル場の微分を基底も含めて微分したものが共変微分なのです。

またシンプルに書き直せば、異なる空間を繋ぎ合わせたファイバーのような構造には、隣との基底のズレを表現する自由度が増え（このために接続が入ります）それに伴い、正しい微分が共変微分

\partial _{\beta} \to \partial _{\beta} + \Gamma^{\alpha}_{\mu \beta}

に置き換わるとも言えます。

最後に接続の座標変換について見ていこうと思います。
構造群、接続は今後は物理での慣習に合わせて

\begin{align}
t_{ij}\in G &\to g\in G\\
\Gamma^{\alpha}_{\mu \beta}&\to A_{\mu}

\end{align}

のように書こうと思います。
まず、ファイバー上での座標変換を考えます。前に述べたように、底空間の局所座標が異なれば、それに伴いファイバーの元が構造群$g\in G$によって以下のように変換されます。

\phi_i = g\phi_j

これらを微分したものも同じファイバーの上の関数なので、同様の変換則が成り立つべきです。微分が共変微分に置き換わることにも注意すると

\begin{align}
\nabla_i \phi_i &=g\nabla_j\phi_j\\
i.e. \ (d+A)\phi_i&=g(d+A')\phi_j
\end{align}

が成り立ちます。こうなると接続の変換則が気になってきますね。
$\phi$の間には構造群$g\in G$による変換

\phi_i=g\phi_j

が成り立つので、接続$A$の間にも何かしらの変換則が成り立ちます。

\begin{align}
\nabla_j\phi_j&=\nabla_j(g\phi_i)\\
&=(d+A')g\phi_i\\
&=(dg+A'g)\phi_i\\
&=g(d+A)\phi_i
\end{align}

最後の等式はそうなるべしという主張です。これが成り立つように$A,A'$について整理すると以下の変換則を得ます。

A'=-(dg)g^{-1}+gAg^{-1}

⁷
ご覧のように、接続と構造群による変換則の関係式が得られました。
実はこの関係式から 構造群$G$がLie群である場合、接続$A$はそのLie代数であることが導けます。　⁸
要はファイバー束の場合、接続$A$と$g\in G$にはとても密接な関係があるということです。

言葉の対応

最後に今まで定義してきた数学の言葉を物理の言葉に言い換えていこうと思います。
今までそれとなく物理の言葉を匂わせてきましたがその答え合わせです。

数学	物理
底空間	時空
ファイバー	場が値を取る空間
切断	場
構造群	ゲージ群
接続	ゲージ場
接続の変換則	ゲージ変換

いかがでしょうか。物理を少し聞いたことがある方は右側について聞き覚えのある言葉が並んでいるのではないでしょうか？
今まで座標変換の整合性から導入した数学の概念が実は物理的なゲージ群やゲージ場という実態を伴っているのです。
果たしてこれはどういうことか？
答えが気になった方はぜひ後編の物理編を読んでみてください。

あとがき　〜これから何をするか？〜

前編を最後まで読んでいただきありがとうございます。数学についての概念の紹介に留まってしまい、人によっては退屈だったり、もしくはわかりにくいと感じた方もいらっしゃると思います。申し訳ありません。
また間違っていたところやより良い理解の仕方があれば是非ご指摘ください。

内容に関して触れれば、ゲージ理論に必要な数学の概念の紹介が一通り終わりました。後編では物理の話をモリモリしていくつもりです。ここからは急ピッチでゲージ理論の美しさに触れていただきます。ぜひ楽しんでください。

【追記】

今週の土曜日に駒場理数サークルの交流会というものを行います。
その際にこの記事の内容を講演予定です。
予定が合えばぜひいらしてください！
https://docs.google.com/forms/d/e/1FAIpQLSfymFlrHn18Gma5ioLxyG9M5pl7D7IAo_JcmYi-icTkyXkgLA/viewform?usp=sf_link

参考文献

ゲージ理論を勉強するにあたり特に数学でためになった本をコメントと共にまとめておきます。
・佐古 彰史　「ゲージ理論・一般相対性理論のための 微分幾何入門」
いい本です。数学の本にしては易しめに書いており特に微分幾何の入門についてもってこいだと思います。ゲージ理論とともに一般相対論の導入もしております。（一般相対論もゲージ理論ですが）

・中原 幹夫　「理論物理学のための幾何学とトポロジーI・II」
これも名著です。ファイバー束の話はII巻に載っています。要所要所に物理の話が書いており良いです。モノポールやソリトンの話も触れています。

・小林　昭七「接続の微分幾何とゲージ理論」
まだほとんど読めていませんが只今駒場でB2や数学科の人を中心にゼミをしております。数学の本らしいです。

1. イカイカ ↩

2. https://astro-dic.jp/gauge-theory/ ↩

3. 数理物理として解決すれば物理に役立つような研究（ミレニアム懸賞問題の一つYang-Mills方程式と質量ギャップ問題などが有名でしょうか）に取り組む方もいらっしゃる一方で物理由来の方程式(Seiberg-Witten方程式など)が多様体の分類を行う道具として使えるために数学としてそれを道具として使って研究を行なっている方もいらっしゃるそうです。 ↩

4. ゲージ理論の一番の創始者Weylは数学基礎論も研究していたそうです。 ↩

5. そういえば自己紹介を忘れていました。私は後期教養統合自然科学科数理自然コースの2年生です。Physics labは理物が中心の団体ですが、僕のような他学部出身の人も受け入れていただいております。ありがたい限りです。
   統合自然科学科について触れておくと、駒場に存在する後期課程の学科で必修が非常に少ないため（今期は1コマのみ）とてものびのびと生活できます。だから忙しいB2のこの時期にこんな記事を書く余裕があるのです
   授業は希望するものを自分で選択できる形になっており、ラインナップとしては理学部ごちゃ混ぜといった印象を受けます。
   先生方は比較的若く、個性的な方や親しみやすい方が多いです。
   自分が進学する際に情報がなく、困った記憶があります。どこかで紹介記事などが書ければと思っていますができるかわかりません。
   疑問などがあれば、Twitterなどで僕を見つけ連絡していただければ答えます。
   また駒場理数サークルという自主ゼミサークル が駒場には存在し、こちらには統合自然科学科の学生が多数存在します。興味があればこちらもTwitterなどで検索してみてください。 ↩

6. 須藤　靖　「一般相対性理論入門」　
   わかりやすく僕はとても気に入っています。 ↩

7. これが後のゲージ変換である。 ↩

8. 坂本　眞人　「場の量子論I」の7章などに載っています。 ↩