はじめに
最近はありがたいことに社内で開発以外の分野に挑戦させていただけることが多くなりました
最近は主に業務内で売上や各種数字からアプリの傾向や売上向上のための施策など分析し、タスクに落とし込む作業に力を入れています
そんな中、文系出身の自分がデータ分析の基礎である回帰分析について学んだので、解説してみたいと思います
(個人開発のアプリの改善や、社内のデータ分析の参考にしていただけると幸いです
)
回帰分析とはなんぞや
回帰分析は、2つ以上の変数の関係を分析する統計手法であり、データ分析においてとても有用な手法の1つです！特に
単回帰分析
重回帰分析
は、ビジネスや経済などの分野で広く用いられています。今回は、単回帰分析と重回帰分析について、基本的な概念や手法について解説してみたいと思います!
単回帰分析
単回帰分析は、1つの説明変数と1つの目的変数の関係を分析する手法です
目的変数が説明変数にどのような影響を受けるかを分析することができます！
どういうときに使うの
例) 商品の売上高を予測したいとき
商品の価格がその商品の売上高にどのような影響を与えるか分析したときに使えます！
例の場合、価格が説明変数、売上高が目的変数となります！
単回帰分析を行うことで、価格と売上高の関係を直線で表現し、その傾向を分析することができます！
重回帰分析
重回帰分析は、2つ以上の説明変数と1つの目的変数の関係を分析する手法です
目的変数が複数の説明変数にどのような影響を受けるかを分析することができます!
どういうときに使うの
例） 商品の売上高を予測していて、価格だけでなく、広告費や季節性など、複数の要因が売上高に影響することが考えられるとき
この場合、価格、広告費、季節性などが説明変数、売上高が目的変数となります。重回帰分析を行うことで、これらの要因と売上高の関係を直線で表現し、その傾向を分析することができます！
実際にどうやって分析するの？
言葉はわかったけどどうやって分析するの！
スプレットシートに目的変数と説明変数を書き出し、「xlminer analysis toolpak」という拡張機能を使うことで表を表示できます！
(もっと良い方法があれば教えていただきたいです
)
※ excelでも可能です！
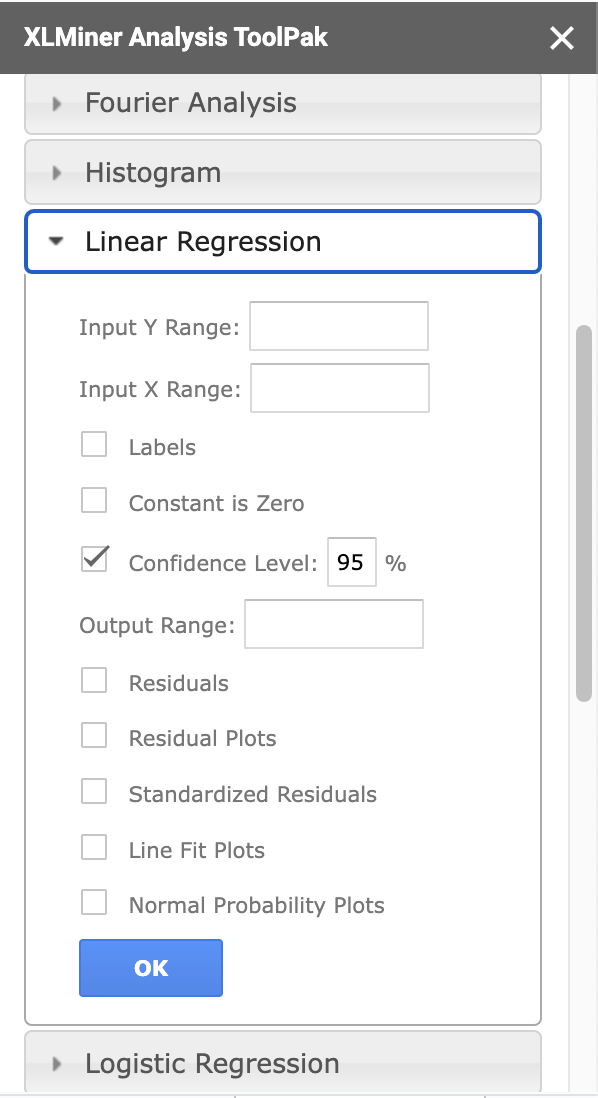
- Input Y Range： 目的変数
- Input X Range： 説明変数
- labelsにチェック
- Output Raｎgeに出力したいセル
でOKを押せば表が出来上がります
出来上がった表がこちら
着目すべき数字は以下です！
１，決定係数 (重決定R2)
決定係数は、回帰モデルが実データにどれだけ適合しているかを表す指標であり、0から1の値を取ります
決定係数が1に近いほど、回帰モデルの予測精度が高いと言えます!
2,自由度調整済み決定係数(補正R2)
補正R2は、説明変数の数にも着目したモデルの適合度を評価することができます!
どうゆうこと？
説明変数を増やせば増やすほど、決定係数は増加する傾向にあります。
説明変数を追加することで決定係数が高くなってしまい、モデルの過剰適合を招いてしまうことがあります
このことを考慮した決定係数が補正R2ということになります
3,係数
回帰分析において、係数は説明変数と目的変数の関係性を表す指標です
単回帰分析では、1つの説明変数が1つの係数に対応します
一方、重回帰分析では、複数の説明変数が複数の係数に対応します
係数の値は、その説明変数が目的変数に与える影響の大きさを表します
具体的には、説明変数が1単位変化した場合に、目的変数がどの程度変化するかを表します!
4, t値(t)
t値が大きい場合、回帰係数の推定値が有意であることを示すため、その説明変数が目的変数に対して有意な影響を与えている可能性が高くなります。一方、t値が小さい場合、回帰係数の推定値が有意でないことを示し、説明変数が目的変数に対して有意な影響を与えていない可能性が高くなります。
5, p-値
p-値は有意性の判定基準として使用される統計的な指標です！
基本的にP値が0.05以下の時に仮説が有意であるとされます
まとめ
今回は、単回帰分析と重回帰分析について解説してみました！
回帰分析は、データ分析において非常に有用な手法の1つであり、ビジネスや経済などの分野で広く用いられています。
単回帰分析は、1つの説明変数と1つの目的変数の関係を分析する手法であり、
重回帰分析は、2つ以上の説明変数と1つの目的変数の関係を分析する手法です！
データ分析に関してはまだひよっこですが、開発の勉強と並行して今後も学習していこうと思います！