Go to Qiita Advent Calendar 2024 Top
LoginSignup
1
3

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 1 year has passed since last update.

@sokono-omae(そこのお前)

【Python／MATLAB】点群のダウンサンプリング関数の仕様の違い

Last updated at Posted at 2023-04-06

1.はじめに

組み込みを行う場合CやC++で記述されることが多いらしいですね。MATLABにはMATLAB CoderといってMATLABで記述されたコードの内容でCやC++コードを自動生成してくれるという便利な機能があります。

私は組み込み方面は門外漢なのですが、以前組み込み方面の担当にPythonコードをMATLABに移行して渡すという作業をしていたことがありました。

その際に同じような動きをする関数なのに同じ入力に対して結果が異なってしまうものについて、その原因とどうしたら同じ結果を得ることが出来るのか、色々と実験してみて分かったことをここにまとめてみます。

今回は点群データのダウンサンプリングを行う関数について調査してみました。

この先長いので、まずは結論からお伝えしましょう。

結論

点群データのダウンサンプリングを行うPythonとMATLABで使用される関数について、PythonでもMATLABでも、点群座標のx軸の最小値、y軸の最小値の座標を基準座標としてダウンサンプリング用のボクセルを作成しているのは共通しています。

ただしPythonではその基準座標を中心としたボクセルを作成するのに対して、MATLABでは基準座標を頂点としてボクセルを作成し、点群のダウンサンプリングを行っています。
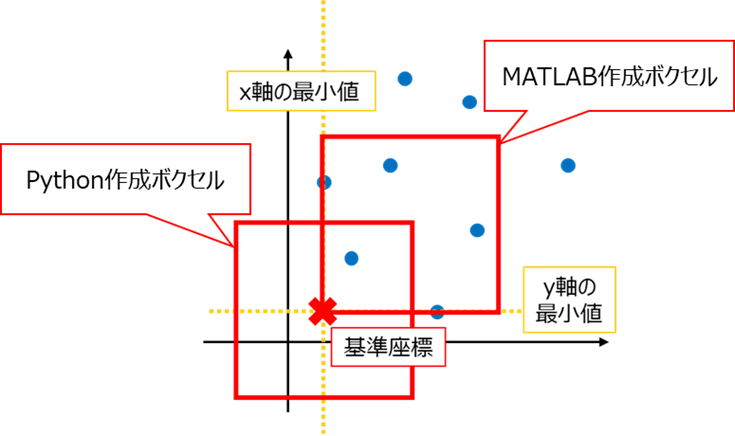
実験結果考察.png
これを利用してMATLAB処理の際に、元々の基準座標が作成されるボクセル位置の中心となるように新たな基準座標となる座標を追加することで、PythonとMATLABの処理結果を一致させることが出来ます。

環境

  • OS：Windows10
  • Python 3.7.13
  • MATLAB 2022b
  • Open3d 0.15.1

※ PythonのコードはJupyter Labを使って動かしています。

2.点群のダウンサンプリングについて

今回行うのは点群データのダウンサンプリングです。一般にRadarやLiderによる観測点の処理を行う際、そのまま全ての観測点を処理しようとすると計算コストが得られる結果に見合わないことが往々にしてあります。そのため、何らかの条件でダウンサンプリングを行うことがあります。

Pythonの場合

使用するのはOpen3dで使用できるvoxel_down_sample関数です。

voxel_down_sample
output = open3d.geometry.voxel_down_sample(input, voxel_size)
# input : 入力点群(open3d.geometry.PointCloud)
# voxel_size : ダウンサンプリングを行うボクセルサイズ

ボクセル内に含まれる点群の重心の座標をダウンサンプリング後の点群として返す関数です。

MATLABの場合

使用するのはComputer Vision Toolboxで使用できるpcdownsample関数です。

pcdownsample
ptCloudOut = pcdownsample(ptCloudIn,'gridAverage',gridStep)
% ptCloudIn : 入力点群(pointCloud オブジェクト)
% 'gridAverage' : ボクセル内の点群の重心を出力とするオプション
%                 'random'を指定するとボクセル内の1点をランダムに出力する
% gridStep : ダウンサンプリングを行うボクセルサイズ

引数としてはほぼ同様ですが、ボクセル内点群の重心を出力とする部分がオプションになっています。'gridAverage'を指定すれば同じ働きをしてくれそうですね。

使用データ

今回はMATLABで乱数発生させた疑似点群を使用します。

make_sample.m
n = 1000;
x = rand(n,1)*10;
y = rand(n,1)*10;
z = zeros(n,1);
points_xyz = [x,y,z];
writematrix(points_xyz,'sample.csv')

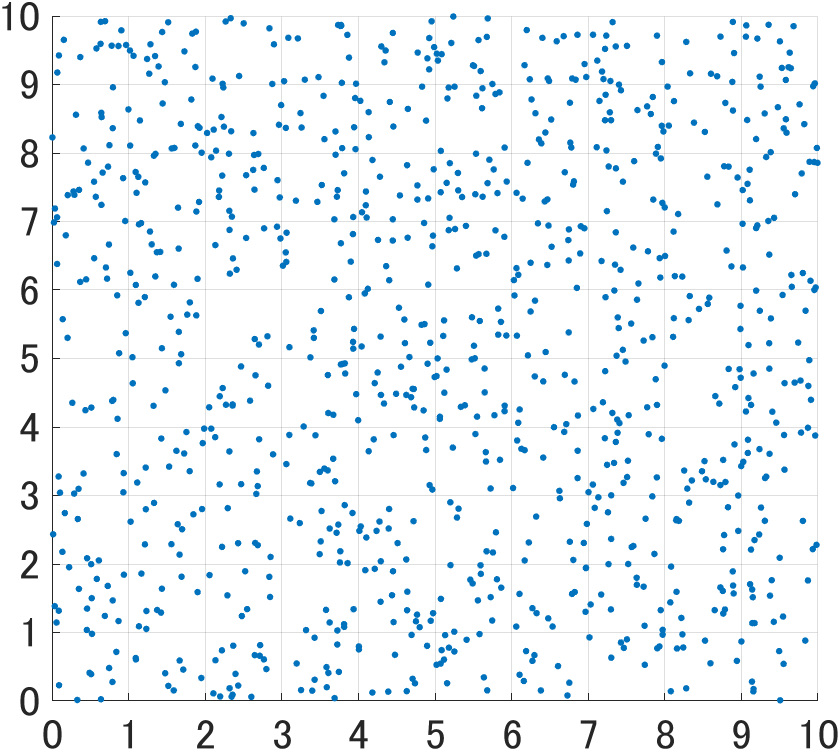
結果が確認しやすいように2次元平面での作成です。MATLAB、Pythonの両方で使用できるようにcsvで保存しています。
図示すると以下のような感じです。
sample.png

3.ダウンサンプリングの実行

まずはそのまま両関数を実行してみます。

PythonDownSampling.py
# モジュールインポート
import numpy as np
import csv
import matplotlib.pyplot as plt
import open3d
# 点群データの読み込み
with open('./sample.csv','r') as f:
    reader = csv.reader(f, quoting=csv.QUOTE_NONNUMERIC)
    points_xyz = [row for row in reader]
points_xyz = np.array(points_xyz)

# ダウンサンプリングの実行
voxel_size = 1
pcd = open3d.PointCloud() #3次元座標を点群データに変換する
pcd.points = open3d.Vector3dVector(points_xyz)
downsampled_xyz = np.asarray(open3d.voxel_down_sample(pcd, voxel_size = voxel_size).points)
# 結果の描画
fig = plt.figure(figsize = (20, 20))
ax = fig.subplots()
ax.set_xlim(0,10)
ax.set_ylim(0,10)
plt.scatter(points_xyz[:,0],points_xyz[:,1],s=100,c="b")
plt.tick_params(labelsize=60)
plt.scatter(downsampled_xyz[:,0],downsampled_xyz[:,1],s=100,c="r")
plt.xticks(np.arange(0, 11, 1))
plt.yticks(np.arange(0, 11, 1))
plt.title("Python DownSampling",fontsize=60)
MATLABDownSampling.m
% 点群データの読み込み
points_xyz = load("sample.csv");
% そのままのダウンサンプリング結果の確認
voxel_size = 1.;
ptCloud = pointCloud(points_xyz); % 3次元座標を点群データに変換する
downsampled_ptCloud = pcdownsample(ptCloud,'gridAverage',voxel_size);
downsampled_xyz = downsampled_ptCloud.Location; % 点群データを3次元座標に戻す
% 結果の描画
fig1 = figure(1);
set(fig1, 'Position', [100,100,1500,900]);
scatter(points_xyz(:,1),points_xyz(:,2),30,"blue","filled"); hold on;
scatter(downsampled_xyz(:,1),downsampled_xyz(:,2),30,"red","filled");
set(gca,'DataAspectRatio',[1 1 1]);
xlim([0, 10]); ylim([0, 10]);
xticks(0:one:10)
yticks(0:one:10)
fontsize(fig1,30,"points")
title("MATLAB DownSampling","FontSize",30)
hold off;

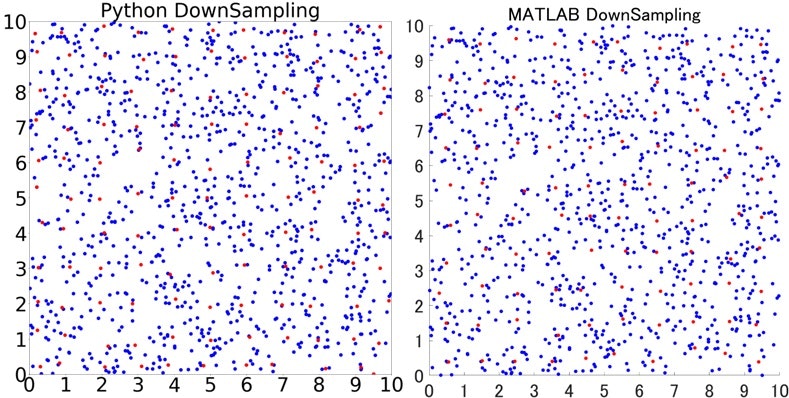
結果はこのような感じに。同じ入力に対して結果が異なっているのが分かるかと思います。
DownSampling_1.png

4.原因の調査

先ほどの乱数発生の点群では何かと分かりづらいので、原因調査のために単純な格子状点群を用いて色々な実験をしてみようと思います。
実験内容は以下の通りです。
実験内容.png

実験結果①-1 ~固定点無し条件の比較①~

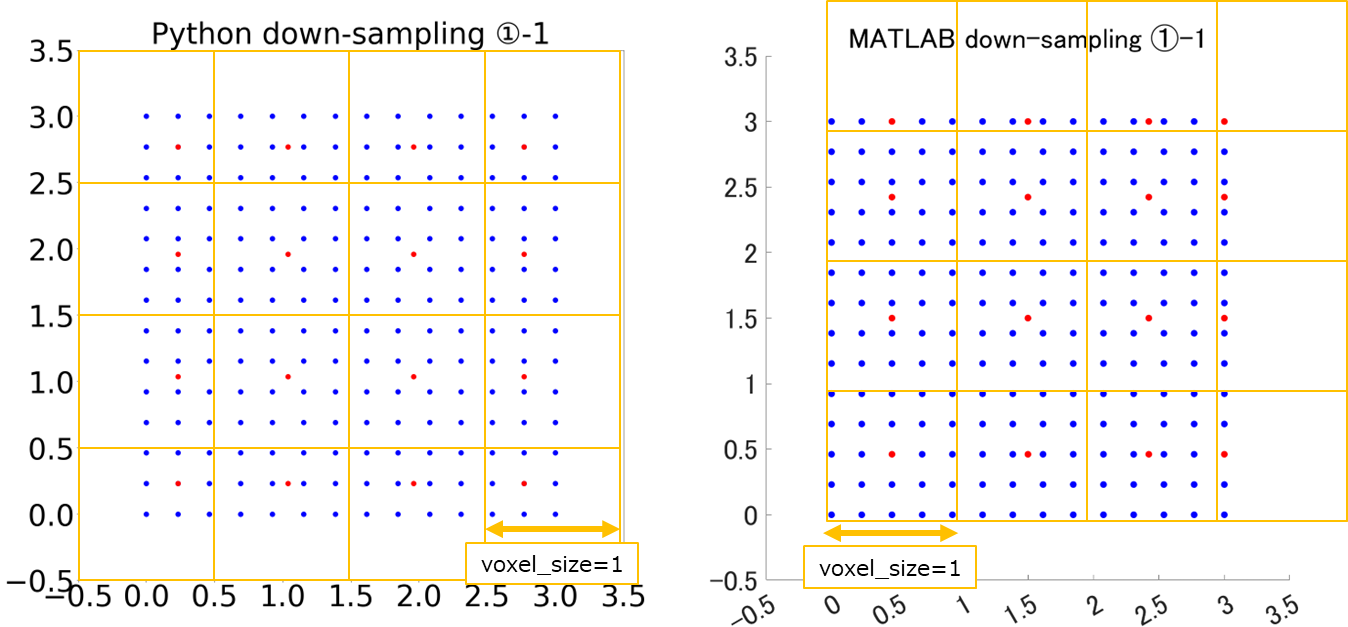
xy平面に0≦[x,y]≦3の範囲で等間隔で14個ずつ、計196個の点を生成しダウンサンプリングを実行。
格子状点群のみの条件では先ほどと同様にダウンサンプリングの結果が異なっており、ダウンサンプリング時に基準となるボクセルの位置が異なっていると考えられます。
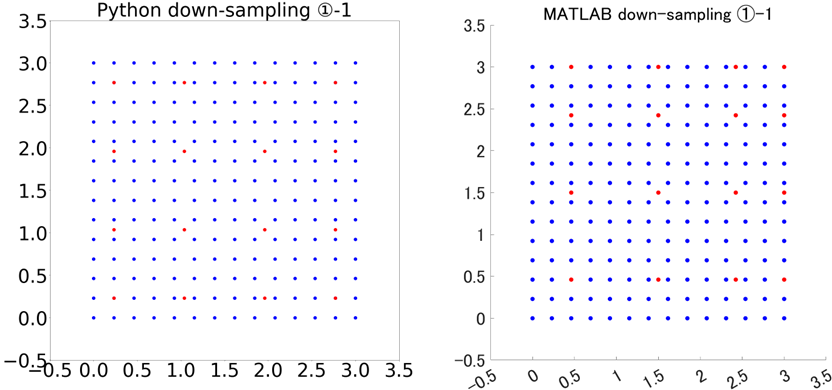
実験結果1-1.png
ボクセル内点群の重心が出力されるというダウンサンプリングの結果から想定されるボクセルの位置を重畳すると、確かに基準となるボクセルの位置がPythonとMATLABで異なっていると言えそうですね。
実験結果1-1.png

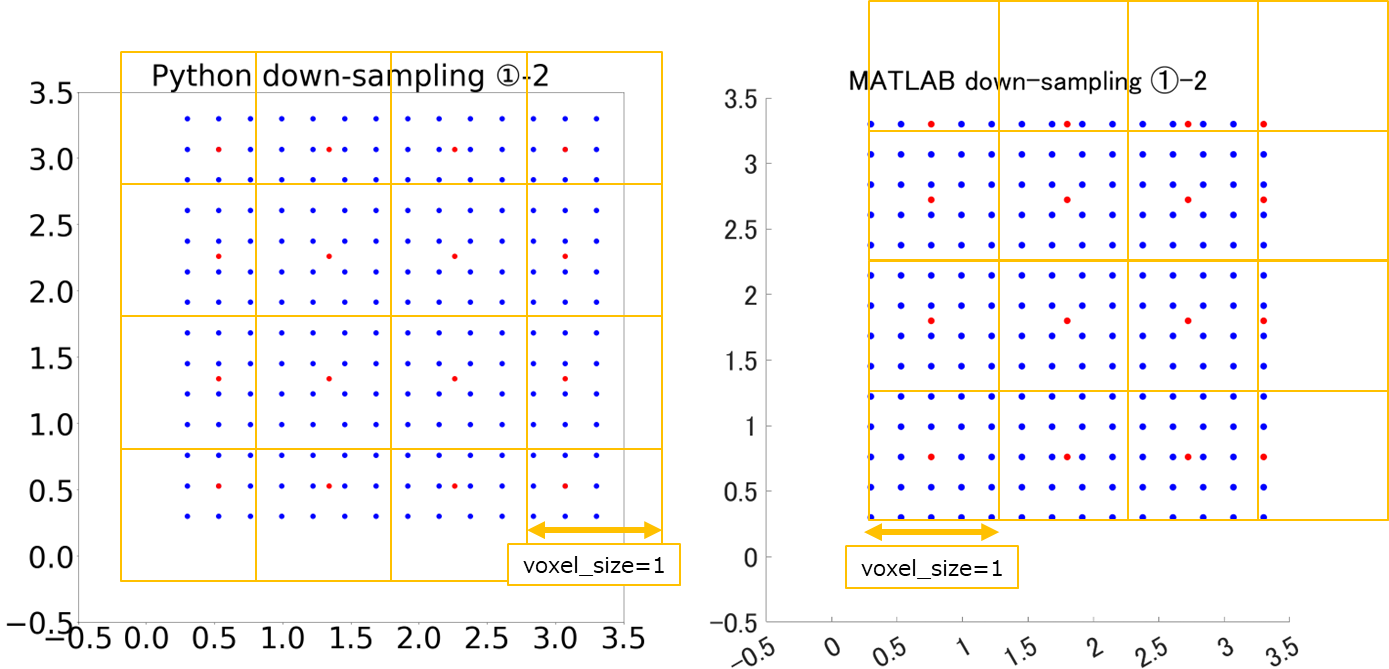
実験結果①-2 ~固定点無し条件の比較②~

試しに点群全体を平行移動させてみたのですが、点群全体とボクセルの相対的な位置関係は変わらないみたいですね。
実験結果1-2.png

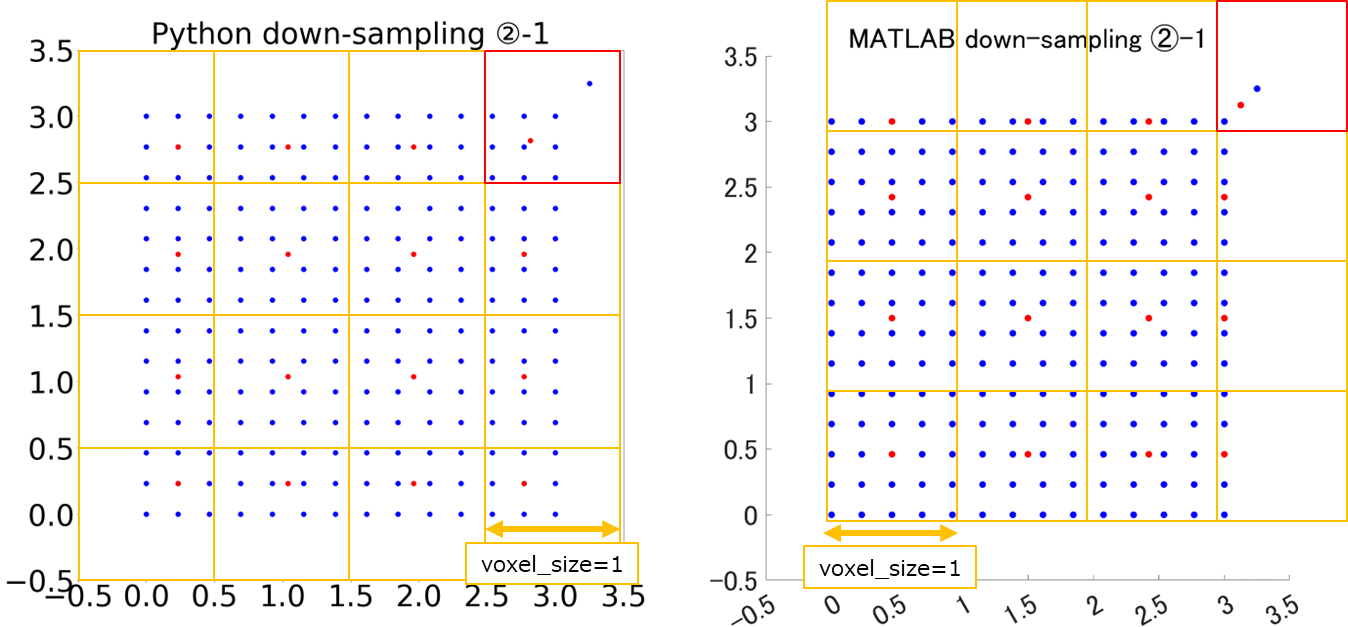
実験結果②-1 ~固定点付与条件の比較①~

次に実験①のダミー点群に点[3.25,3.25]を追加し、他の条件は同一にしてダウンサンプリングを行ってみました。
変化が生じたのは実験①にて点[3.25,3.25]が含まれていたボクセルのみであり、その他のボクセルのダウンサンプリング結果には影響していないみたいです。
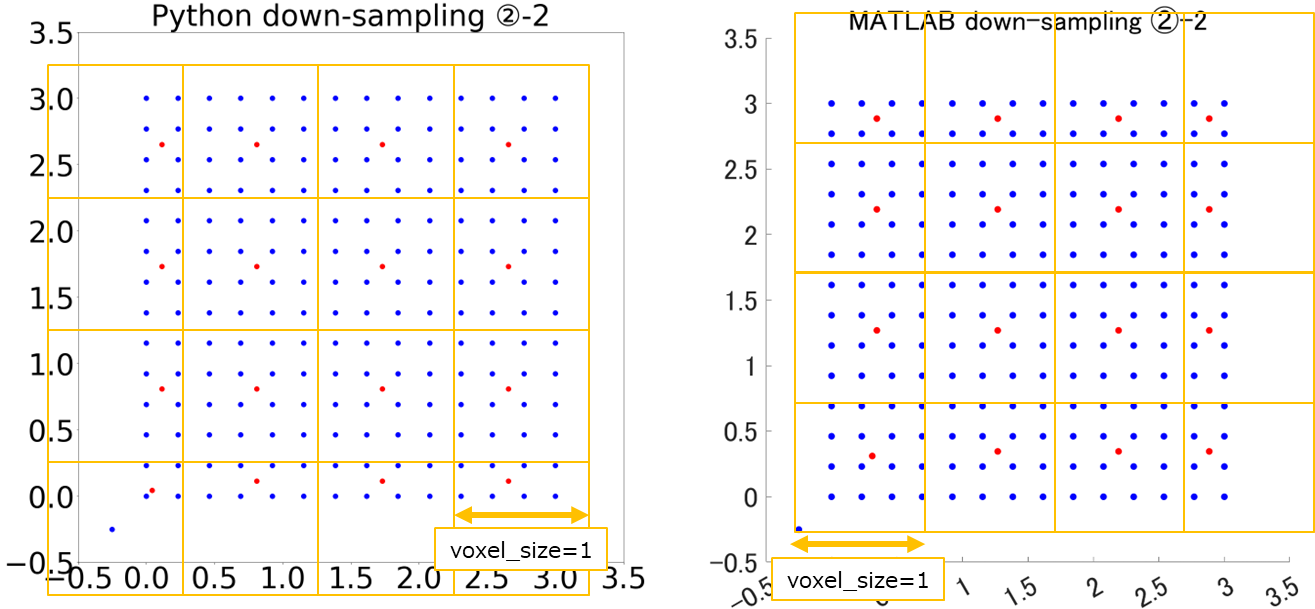
実験結果2-1.png

実験結果②-2 ~固定点付与条件の比較②~

次に実験①-1のダミー点群に点[-0.25,-0.25]を追加し、他の条件は同一にしてダウンサンプリングを行ってみました。
実験結果②-1とは異なり、固定点が含まれるボクセルだけではなく、全てのダウンサンプリング結果に実験①-1との相違が見られました。
これは、点[-0.25,-0.25]を追加したことにより、図のようにボクセル作成のされ方自体が変化したと考えられますね。
実験結果2-1.png

実験結果②-3 ~固定点付与条件の比較③~

次に実験①-1のダミー点群に固定点[3.25,-0.25]を追加し、他の条件は同一にしてダウンサンプリングを行ってみました。
実験結果②-2と同様にボクセルの作成のされ方が変化した様子が見られますが、追加点が含まれるボクセル以外で変化しているのはダウンサンプリング結果座標のうちyの値のみでxの値は変化していないようです。

結果は省略しますが、対称的に点[-0.25,3.25]を追加して実験を行うと、xの値のみが変化し、yの値は変化しませんでした。
実験結果2-1.png

実験結果の考察

実験結果①-2からボクセルの作成方法は入力点群の座標に依存しているということが分かりました。
また、実験結果②から固定点を付与した場所によってボクセル作成のされ方の変化に特徴が見られましたが、与えた固定点がボクセル全体に与えた影響を確認してみましょう。
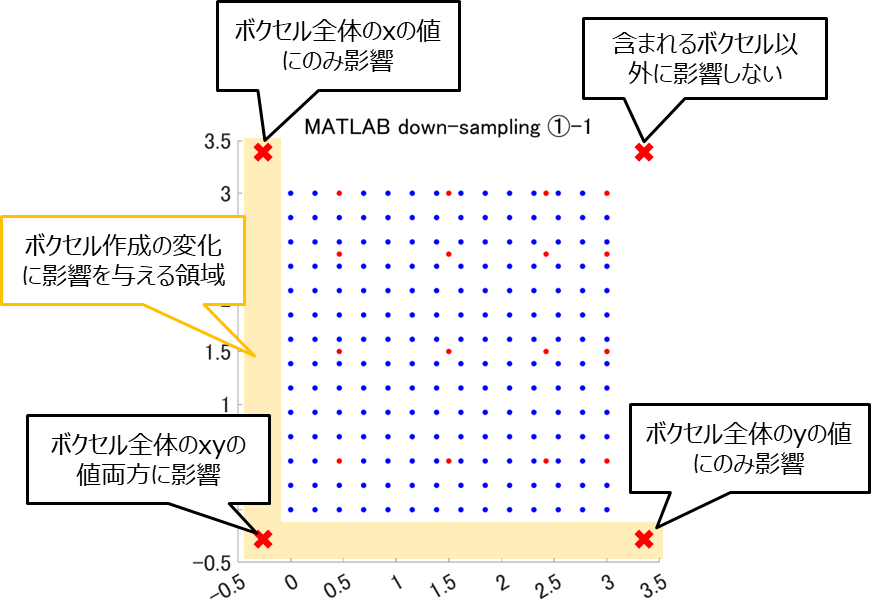
実験結果考察.png
上の図を見てみると、ボクセルの作成はx,yそれぞれの軸の最小値の座標に依存していると考えられ、この仕様はPython、MATLABで共通であると言えそうです。
さらに、ここまでの実験結果からPythonでは上記の基準となる座標を中心としたボクセルを作成しており、MATLABでは基準となる座標を頂点としたボクセルを作成していると考えられます。
実験結果考察.png

実験③ ~MATLABのダウンサンプリング結果を制御する~

Python、MATLABでダウンサンプリングの仕様が理解できたため、実際に学習を行っているPythonの結果にMATLABの結果を合わせる方法について追加で検討してみましょう。

結局ボクセルの作成結果がPythonの結果と一致すれば良いので、入力点群におけるx,yそれぞれの最小値に該当する座標がボクセルの中心となるように、MATLABの処理の中で座標を追加してボクセルの位置を操作するのが最も簡単だと思われますが、安易に座標を追加してしまうとダウンサンプリングの結果そのものに影響してしまうため、追加する座標は慎重に選択する必要があります。
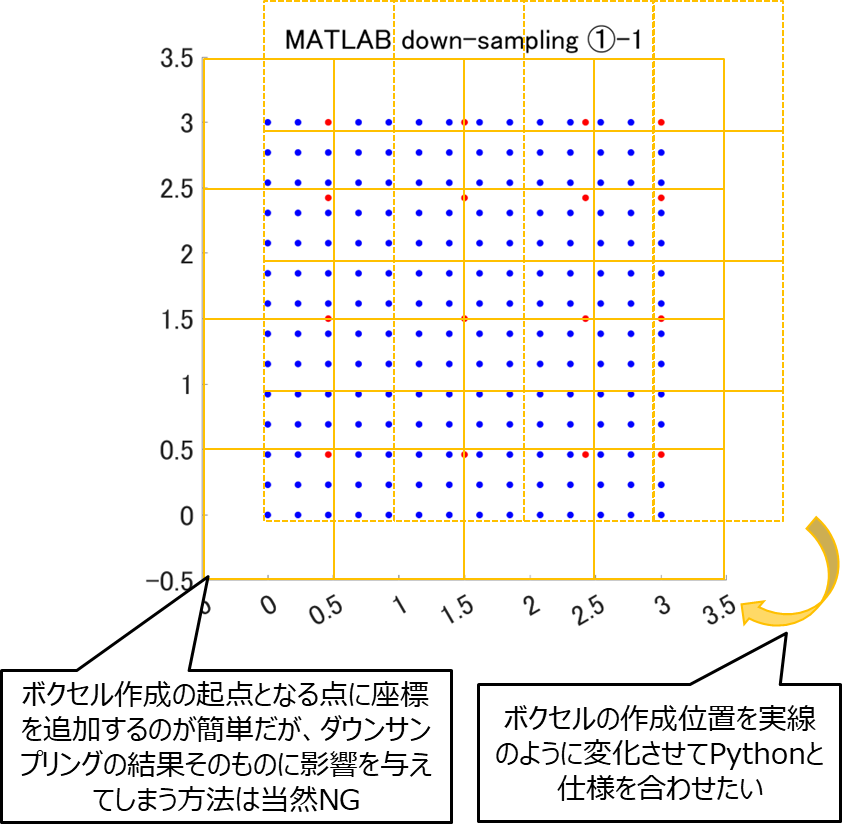
実験結果考察.png
そのため、ダミー点群とsampleデータを用いて、MATLABにてダウンサンプリング結果そのものには影響を与えず、ボクセルの作成位置を制御する処理方法について検討してみました。

実験結果③-1 ~MATLABのダウンサンプリング結果を制御する~

一番簡単な考え方としては入力点群のxy座標それぞれの最小値からvoxel_sizeの0.5倍の値を引いた座標を追加すれば、MATLABにおけるボクセル処理の仕様に従って、追加した座標がボクセル作成の起点となってくれるはずです。

実際、座標追加前のボクセル作成の基準座標がPythonの仕様と同様にボクセルの中心に位置するようにできます。
しかし、この方法では追加した座標も入力点群と同一のボクセルに含まれてしまうことになります。
これでは元々のダウンサンプリング結果に影響を与えてしまうので当然不適ですね。

次に簡単な考え方として、さらにもう1ボクセル分離れた位置(最小値からvoxel_sizeの1.5倍の値を引いた位置)に座標を追加すればダウンサンプリング結果そのものに影響を与えずにPythonと同様の処理を行うことができそうですね。
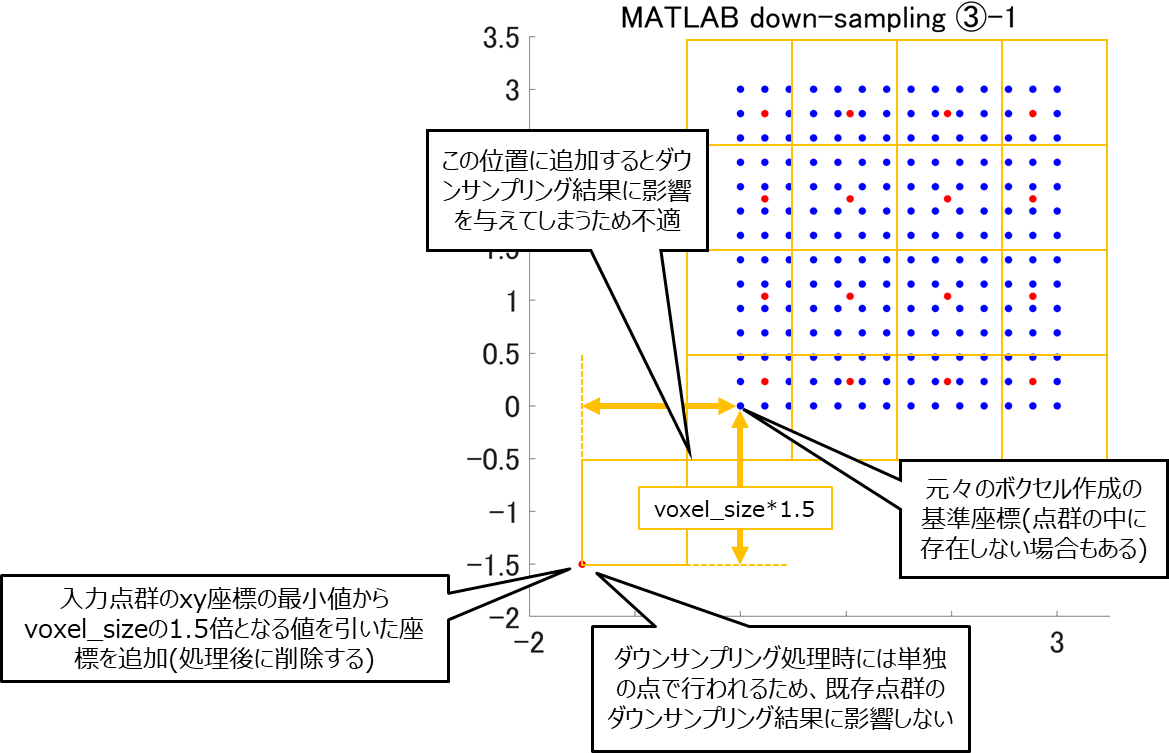
実験結果考察.png
ここで追加した座標はダウンサンプリング処理後に削除すればよいでしょう。追加した座標はダウンサンプリング後でもx,y座標ともに最小値をとっているはずなので削除は容易なはずです。

sampleデータで確認してみます

MATLABDownSampling_cor.m
% 点群データの読み込み
points_xyz = load("sample.csv");

% Pythonと処理を合わせるために座標を追加する
min_coord = min(points_xyz);
add_min_coord = min_coord-1.5*(voxel_size);
points_xyz_add = [points_xyz;[add_min_coord(1),add_min_coord(2),0]];

% そのままのダウンサンプリング結果の確認
voxel_size = 1.;
ptCloud = pointCloud(points_xyz); % 3次元座標を点群データに変換する
downsampled_ptCloud = pcdownsample(ptCloud,'gridAverage',voxel_size);
downsampled_xyz = downsampled_ptCloud.Location; % 点群データを3次元座標に戻す

% 処理を合わせるために追加した座標を削除
downsampled_xyz(find(min(downsampled_xyz(:,1))),:) = [];

% 結果の描画
fig1 = figure(1);
set(fig1, 'Position', [100,100,1500,900]);
scatter(points_xyz(:,1),points_xyz(:,2),30,"blue","filled"); hold on;
scatter(downsampled_xyz(:,1),downsampled_xyz(:,2),30,"red","filled");
set(gca,'DataAspectRatio',[1 1 1]);
xlim([0, 10]); ylim([0, 10]);
xticks(0:one:10)
yticks(0:one:10)
fontsize(fig1,30,"points")
title("MATLAB DownSampling","FontSize",30)
hold off;

Pythonの結果と比較してみるとこんな感じです。
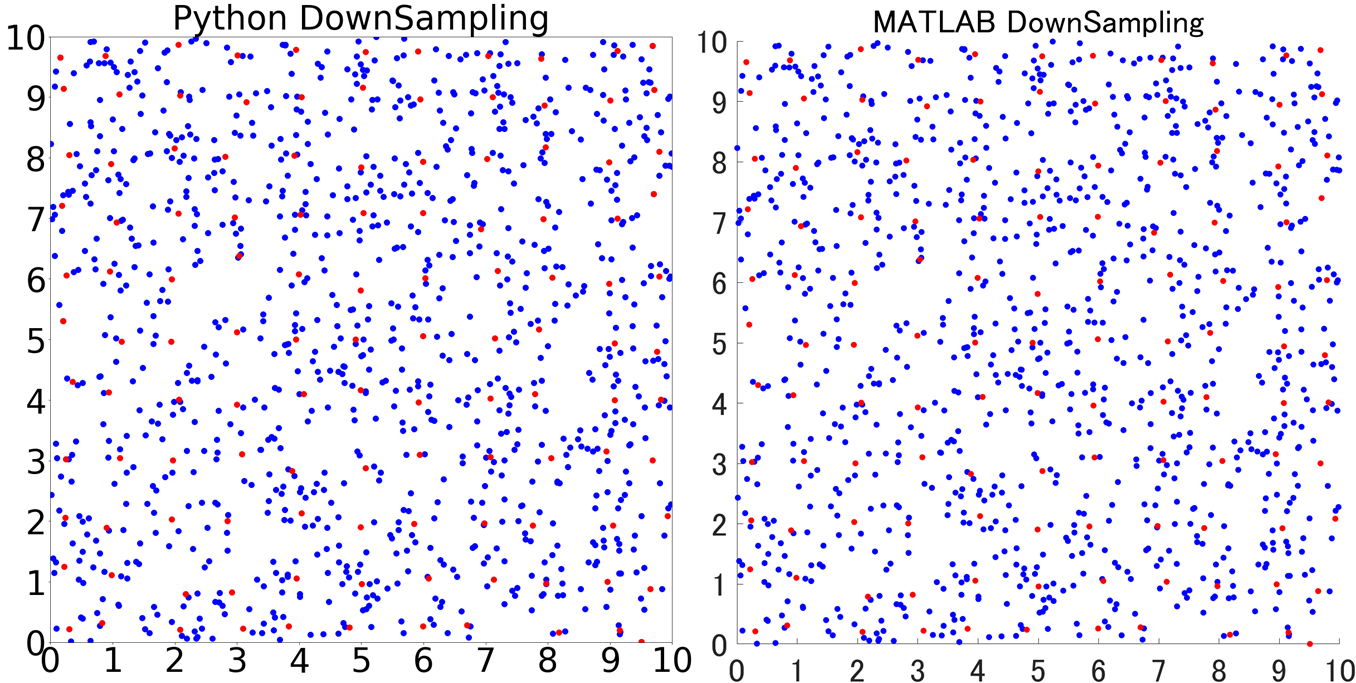
DownSampling_2.png
やりました！これは一致していると言ってもいいでしょう！

5.まとめ

今回は点群データのダウンサンプリングを行う関数について、PythonとMATLABで使用される関数の仕様の違いについて調査してきました。

結論としてPythonでもMATLABでも、x軸の最小値、y軸の最小値の座標を基準としてボクセルを作成しているのは共通していますが、Pythonでは基準座標を中心としたボクセルを作成するのに対して、MATLABでは基準座標を頂点としてボクセルを作成し、点群のダウンサンプリングを行っていることが分かりました。

これを利用してMATLAB処理の際に、元々の基準座標が作成されるボクセル位置の中心となるように新たな基準座標となる座標を追加することで、PythonとMATLABの処理結果を一致させることが出来ます。
実験結果考察.png

1
3
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
3

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?